基于机器视觉的手持式瓦楞纸计数系统研究

夏立元，王沛龙，赵宏，肖昌炎，李树涛

工业机器视觉

基于机器视觉的手持式瓦楞纸计数系统研究

夏立元1，王沛龙1，赵宏2，肖昌炎1，李树涛1

（1.湖南大学 电气与信息工程学院，长沙 410082；2.国防科技大学 空天科学学院，长沙 410073）

为了实现对瓦楞纸叠层的精确计数。提出一种基于机器视觉的手持式计数系统，介绍了系统的硬件组成和应用场景，引入孔洞增强算法和基于倾斜校正的孔洞投影策略，并且与现有计数算法进行对比分析，最后针对不同楞型的瓦楞纸叠层进行计数实验，进一步验证了所提出算法的鲁棒性。对已有不同楞型的瓦楞纸进行多次试验，提出的计数系统均能取得99%的准确率。在实际工作场景下，大量测试表明该系统可以对瓦楞纸叠层进行精确计数。

瓦楞纸叠层；机器视觉；海森矩阵；孔洞检测

瓦楞纸因其较好的强度和缓冲性能通常被作为包装材料。近年来对瓦楞纸板的需求逐年递增[1]，制造行业正在寻求利用机器视觉[2]的方法提高生产效率。目前部分无接触式的计数方法是通过传感器得到瓦楞纸叠层的高度，再除以单张瓦楞纸的厚度得到层数[3]，但是实际应用中，因为受潮和受力等原因，每张瓦楞纸板间的厚度均有一定差异，因此最终计数误差较大。当前主流的无接触式计数方式多采用基于机器视觉的方法，有关瓦楞纸叠层计数的论文中，针对瓦楞纸叠层堆叠高度高、纸板排布密集的这一特性，通常采用伺服电机带动线扫描相机，通过逐层扫描的方式来对瓦楞纸叠层端面进行成像，这样每次只聚焦于瓦楞纸叠层中的部分区域，可以得到较高的成像质量。Suppitaksakul等[4]通过二值化和连通域检测[5]来提取瓦楞纸中的孔洞特征，以实现计数。黄丹平等[6]通过小波变换来提取瓦楞纸中波浪线状纹理，以实现计数。通过逐层扫描得到的图像通常对比度较高，纹理特征较为明显，因此算法往往能取得不错的效果。然而线扫描相机价格昂贵，成像方式严重依赖于机械结构，导致图像获取时间长，测量效率低。同时实际工作场景需要对组合楞型的瓦楞纸进行计数，此时图像的频率特性较为复杂，基于频域的小波变换难以取得较好的效果。近年来，人们开始将深度学习的方法应用到瓦楞纸计数中[7-8]，通过在大量的数据集上进行训练，深度学习的算法能够在组合楞型的瓦楞纸上取得不错的计数效果，但这些方法通常对系统运算能力有较高的要求，且收集对应的数据集进行标注需要花费大量人力成本。

文中提出一种手持式计数系统，利用面阵相机一次性对整个瓦楞纸端面进行成像，不依赖于额外的机械结构。相比于线扫描相机逐行扫描的成像方式，这种成像方法得到的图像质量有所下降，因而目前已有的算法往往不能在这些图像上取得较好的效果。针对这一问题，文中提出一种基于多尺度孔洞检测的瓦楞纸计数算法，在所采集的图像对比度较低、纹理特征不明显的情况下，也能实现准确计数。

1 手持式瓦楞纸计数系统硬件结构

手持式瓦楞纸计数系统主要由3个部分构成。相机和光源构成成像系统，树莓派芯片构成了算法处理系统，红外测距传感器、触控显示屏等构成了交互系统。整个系统的工作示意图见图1。

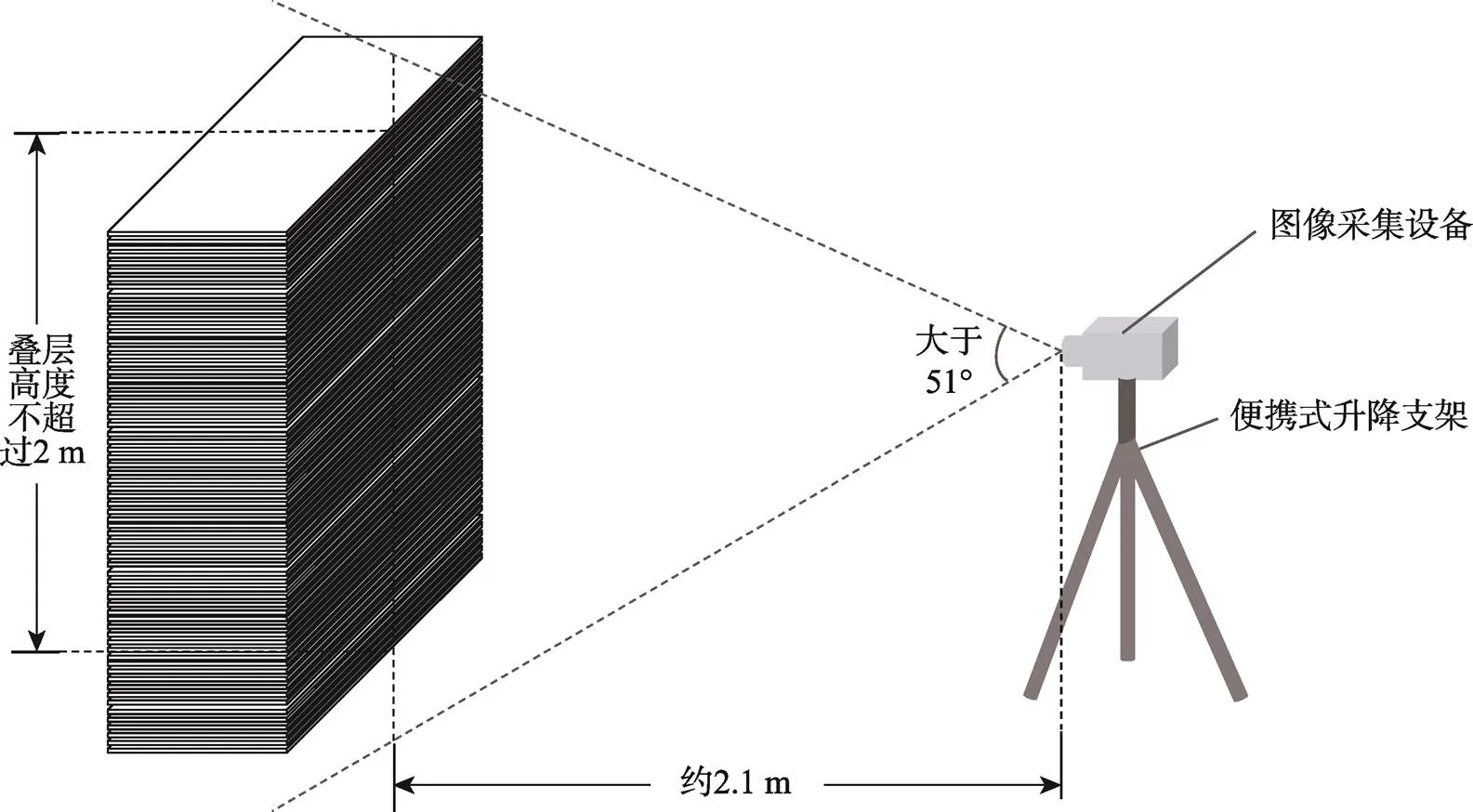
图1 计数系统工作示意图

成像系统使用单个面阵相机对瓦楞纸叠层图像进行采集，瓦楞纸叠层高度一般为2 m，在拍摄距离为2.1 m左右时，相机的视场能够覆盖到整个瓦楞纸叠层区域。同时为了使成像对比度更高，需要使用额外光源对瓦楞纸进行补光，以保证在不同场景下的成像质量。系统的设备结构示意图见图2。

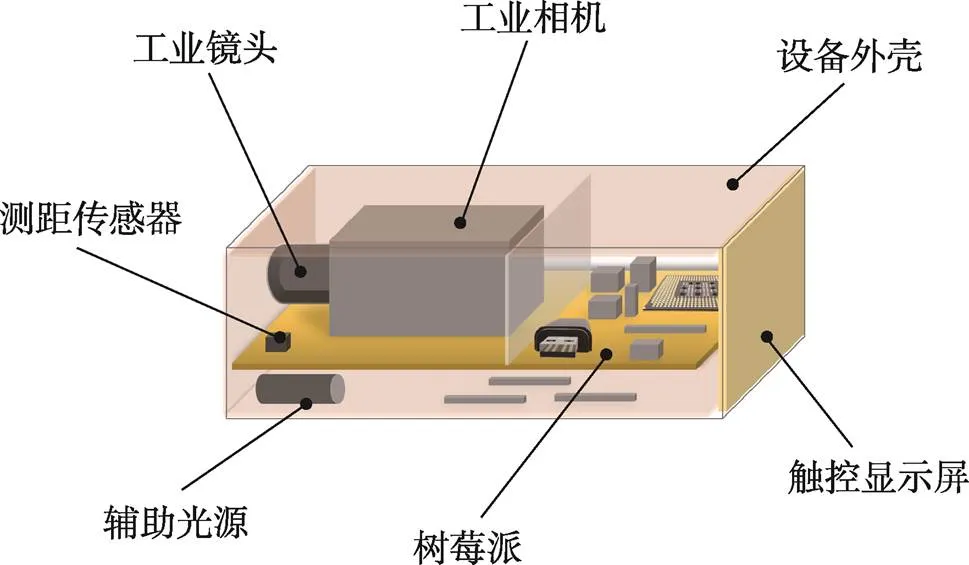
图2 图像采集设备结构示意

2 瓦楞纸计数算法

算法流程见图3，首先通过高分辨率的面阵相机对整个瓦楞纸叠层进行成像，取代了现有计数设备使用的由伺服电机带动线扫描相机进行成像的方案。面阵相机的成像质量较差，因此需要对所拍摄的图片进行预处理，以提升图像的对比度，后续所采用的多尺度孔洞增强算法，可以增强低对比度下各种不同型号的瓦楞纸孔洞。提取孔洞后，将孔洞沿着水平方向进行投影，通过对投影的结果进行峰值检测来对瓦楞纸叠层进行计数。

2.1 预处理

由于手持式设备的光源功率受到一定限制，加上需要和待测纸堆保持一定的距离，才能在相机的视场范围内拍摄到完整的瓦楞纸叠层目标，所以实际拍摄的图像通常整体较暗，对比度较低，需要对图像进行局部直方图均衡化。局部直方图均衡化是把图像划分为不同的子块，在每个子块中进行直方图均衡化，这样能够使得图像的局部细节和对比度得到充分增强[9]。原始图片见图4a，局部直方图均衡化后的效果见图4b。

2.2 瓦楞纸叠层区域提取

成像设备采集的图像中除了瓦楞纸叠层，通常还有其他的非感兴趣区域，如放置瓦楞纸的木质垫板。利用瓦楞纸的纹理特性可以较快速地区分纸张区域和非纸张区域，准确地分割纸张区域和非纸张区域，有利于排除一些不必要的噪声干扰。如图5所示，根据瓦楞纸楞边灰度分布情况，创建具有对角线纹理模式的卷积核，进一步增强纸张区域的纹理，抑制非纸张区域的纹理，所采用的卷积核见式（1）。

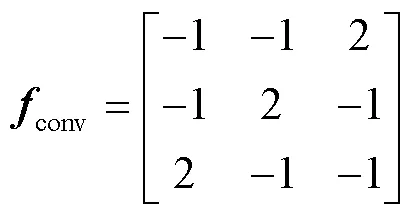
初步卷积结果见图6b，纸张区域的纹理得到显著增强，但是非纸张区域仍有一些噪声干扰，可以通过小连通域检测和二值化的方法滤除这些噪声干扰，见图6c。最终通过形态学膨胀的方法分割出纸张区域和非纸张区域，见图6d。

2.3 孔洞增强

提取完整的瓦楞纸纸张区域后，通常通过检测瓦楞纸图像中的直线[10]或者孔洞特征实现计数[11]。在实际的瓦楞纸叠层中，瓦楞纸板间会存在一定的间隙，在正常情况下，2张瓦楞纸板间只显示出一条直线，而在缝隙处2张纸板间显示出2条直线，因此利用直线特征进行计数很容易引入误差，而孔洞和每张瓦楞纸则有较好的对应关系。

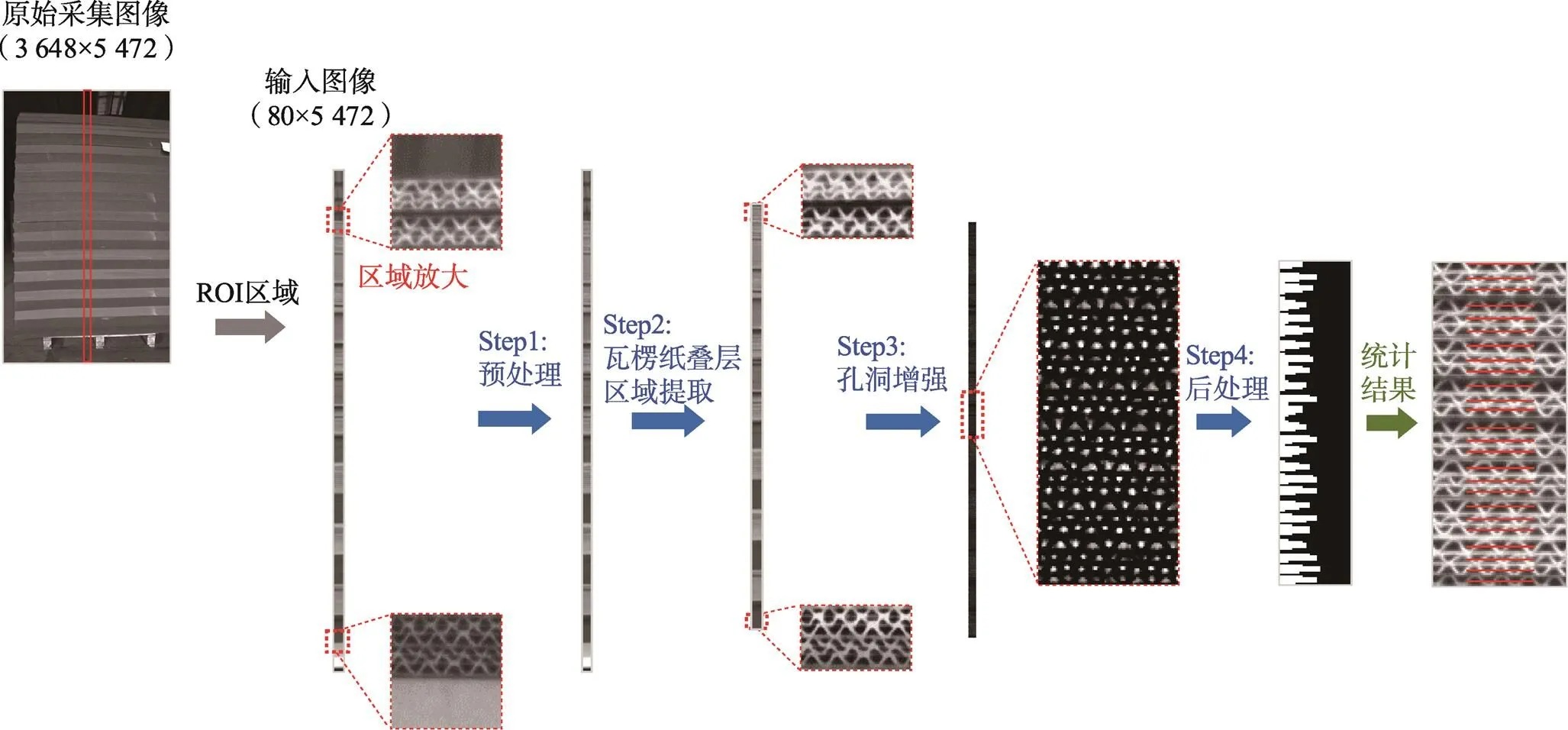
图3 计数算法流程

图4 局部直方图均衡化前后的图片

图5 瓦楞纸楞边灰度分布

图6 纸张区域提取

瓦楞纸中的孔洞是一种近似半圆形的结构，且灰度值较低，直方图均衡化后孔洞周围楞边的灰度值均明显高于孔洞内部，求取海森矩阵可以进一步增强孔洞的结构[12]。海森矩阵对应着图像在某点处灰度值的二阶导数，反映了图像灰度梯度变换程度。直接将海森矩阵作用在图像上往往会放大图像中的噪声。为了减少这些干扰，在求取海森矩阵之前，需要使用低通高斯滤波器对图像进行平滑处理。图像处理领域中，通过对二维高斯核求取各个方向上的二阶导数，将高斯平滑和求取海森矩阵这2个卷积操作变为1个卷积步骤，高斯核各个方向上的二阶偏导数分别见式（2）—（4）。其中式（2）的二维高斯函数在方向上的二阶偏导数图像见图7。

式中：和为像素坐标；为高斯函数对应的标准差。

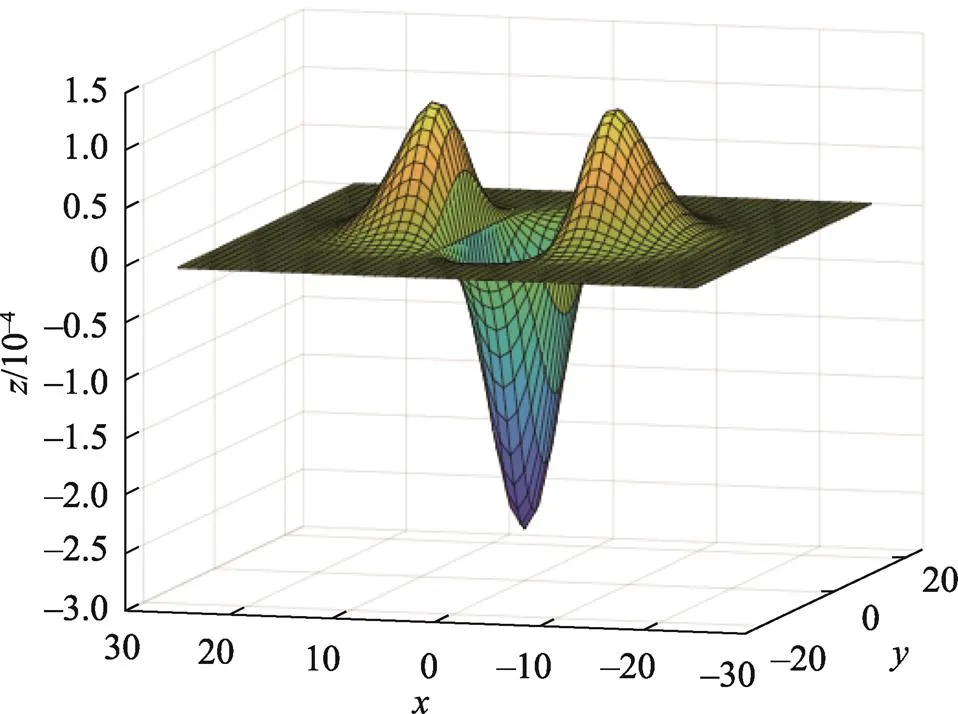
图7 二维高斯函数在x方向上的二阶导数

在二维图像中求取海森矩阵得到的2个特征值中，最大特征值与其对应的特征向量表示其二维邻域曲线最大曲率的强度和方向，最小特征值对应的特征向量表示与其垂直的方向，即图像某点处海森矩阵特征值的大小和符号，直接反映了该邻域内的几何结构。理想圆形孔洞的海森矩阵特征值具有各向同性，即2个特征向量的模值较大，且取值也比较接近。在瓦楞纸板中提取出的孔洞，通常形状不规则，孔洞内部某些位置处的特征值可能无法体现各向同性。同时受成像设备和光源的限制，图像某些位置的对比度可能较低，在这种情况下，孔洞位置对应的海森矩阵特征值和其他位置处的特征值间没有显著的差异，此时增强孔洞很容易引入噪声干扰。

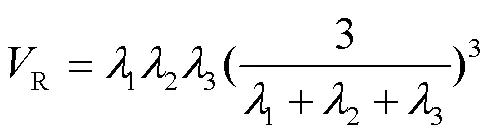
式中：1、2、3分别为三维海森矩阵的3个特征向量。

经过上述分析，设计如式（7）所示的孔洞响应函数，其本质上仍是体积比的形式，但是二维图像只有2个特征值，并且其中的部分特征值根据纸张孔洞的实际形状进行了更有针对性的归一化。

以C楞型的瓦楞纸为例，对孔洞响应的结果进行分析。实际采集的图像见图8a，上半部分区域对比度较低，楞边几乎不可见。图8b为局部直方图均衡化后的结果，上半部分区域中孔洞和楞边的对比度得到较大提升，但整体仍然较为模糊。图8c为孔洞增强的结果，可以看出基本上所有孔洞均被孔洞响应函数增强，图像下半部分成像清晰，孔洞响应较大，直观体现为灰度值强度较大。上半部分较模糊区域中，大部分孔洞仍有较大的响应，部分孔洞响应较小，在图8c中灰度值强度较暗。高对比度区域孔洞响应结果见图8e，孔洞响应输出的最大值为0.58，最小值为0.06。图8d为低对比度区域孔洞响应放大图，其中响应输出最大值为0.25，最小值为0.06。因为孔洞增强前进行过平滑处理，并且对海森矩阵的特征值进行了归一化，所以在低对比度区域的孔洞得到增强的同时，并未引入其他非孔洞区域的噪声干扰。

2.3.1 复合楞型与多尺度问题

实际生产中除了单楞型，通常还会有双楞和三楞组合的混合楞型，如B楞和E楞组合形成BE楞，因此需要考虑多尺度问题。根据尺度空间的理论，调节生成的海森卷积核中高斯函数的标准差，可以使得卷积核作用后突出不同尺度下的特征。具体到瓦楞纸叠层测量中，需要根据不同型号的瓦楞纸设置标准差，以突出不同楞型的孔洞。

以实际应用中的B楞和E楞为例，E楞的高度范围约为6～8个像素，B楞的高度范围约为14～16个像素。只有卷积核的尺度和对应楞型的尺度相近时才能达到最好的卷积效果。如果使用卷积核的尺度远大于孔洞的尺度，多个小孔洞被一个大尺度的卷积核卷积则造成孔洞的粘连，同时会引入更多的背景噪声。同理使用小尺度的卷积核去卷积大尺度的孔洞，如利用E楞对应的尺度去卷积B楞对应的孔洞，则B楞孔洞提取不完整，原本一个孔洞会被分割为多个更小的孔洞。

针对BE的组合楞型，需要使用2个不同的尺度的卷积核分别去做卷积，得到2张卷积图像后，在每个像素位置，选择响应值最高的作为最终的卷积结果[15]。图9为经过直方图均衡化后BE组合楞型图片，分别针对B楞型和E楞型设置2个不同尺度的高斯卷积核，最终结果见图10。

图8 不同对比度区域孔洞响应

图9 BE组合楞型

图10 BE孔洞提取

2.4 后处理

孔洞增强结果中孔洞的形状大小均不一致，在进行投影操作时很难设置相应的阈值，因此首先通过计算轮廓矩的方式提取每个孔洞的重心坐标。灰度图像中通过计算零阶矩和一阶矩来获取轮廓重心坐标，计算公式分别为：

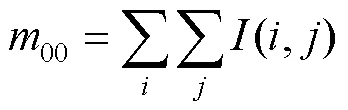
轮廓重心计算公式为：

重心提取完成后，以每个孔洞重心为圆心，生成一个半径为2像素的圆形。此时所有孔洞对应的形状大小均相同，图11为孔洞大小标准化前后的效果。以C楞为例，在截取的80宽度的像素区域中，每行应该有8～9个孔洞，考虑在某些低对比度的区域中可能有部分孔洞未能检出，规定至少检出3个以上的孔洞，才确定该区域对应一张瓦楞纸。对于C楞，在沿水平方向投影的过程中小于这一阈值的投影结果设置为0，将一维投影结果以柱状图的形式显示，图12b为沿水平方向投影结果，为排除噪声干扰，对于不同楞型瓦楞纸的水平投影结果，分别用对应各自楞型高度的一维高斯滤波器进行平滑，平滑的结果见图12c。为进一步验证算法的可靠性，将孔洞提取结果以及水平投影结果显示在同一张图上，见图13，可见对于框出的纸张严重变形区域，虽然所检测出的孔洞较小，部分孔洞未能检出，但是在进行孔洞大小标准化后，投影的结果中依然可以检测到明显的峰值。

图11 孔洞处理

图13 孔洞提取与投影结果

2.5 倾斜矫正

瓦楞纸在堆放的过程会出现倾斜问题，但在算法处理的过程中往往只截取较短的一段宽度进行投影，因此在目前所采集的图片中倾斜问题不会对投影结果造成太大的偏差，图14为现有算法在纸张倾斜的图像上运行的结果，可见虽然瓦楞纸有一定程度的倾斜，投影结果中柱状图的峰值区域和瓦楞纸叠层中的每张瓦楞纸仍有较好的对应关系。

图14 算法投影结果

在倾斜程度较大的情况下，水平投影较容易产生误差，因此结合实际情况对倾斜问题进行进一步分析。在实际的生产中，瓦楞纸很少整体往某一方向倾斜，通常越往顶部区域越容易发生倾斜，并且不同区域的倾斜方向可能不同，因此从算法适用性的角度来说，倾斜问题不能简单通过沿着某一方向进行投影来解决。

同一瓦楞纸叠层中，瓦楞纸不同方向的倾斜需要进行不同的校正，因此借鉴图像拼接的算法来对倾斜情况进行校正。图像拼接中首先通过SIFT算子查找2张图像中匹配的特征点，然后利用这些特征点求取单应矩阵，通过单应变化将一张图像对齐到另一张图像的坐标系下。在孔洞标准化后的图像上应用霍夫检测可以快速得到不同区域中倾斜角度不同的直线，如图15所示，其中上端白色的线为霍夫检测得到的结果，期望倾斜校正后白色线上的点能够移动到下端水平的橘黄色直线上，因此可以把白色直线的2个端点和橘黄色直线的2个端点看作是原始图像和校正后图像中的一对匹配点，白色直线的2个端点可以直接利用霍夫检测提供的角度信息求出，而橘黄色直线的两个端点纵坐标和白色直线左端点的纵坐标相同，横坐标分别为0和图像的宽度。这样通过霍夫检测在原始图像中的不同区域分别检测出4条直线，就可以提供8对匹配点，利用这些匹配点求出单应矩阵后，通过对原始图像进行单应变换，可以得到校正后的图像。

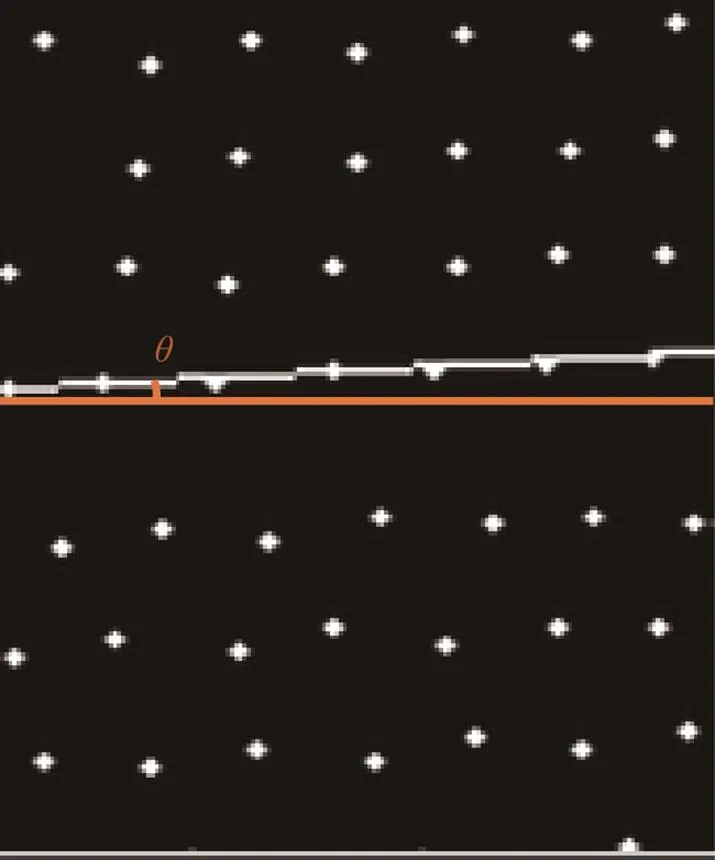
图15 孔洞标准化图像上的霍夫检测结果

如图16所示，在图像的不同位置选取4条直线，4条直线中除了第一条直线向下倾斜，其他直线基本水平或轻微向上倾斜，这也反映了瓦楞纸叠层中不用区域瓦楞纸的实际倾斜情况。通过这4条直线可以得到8个匹配点，利用这8个匹配点可以计算出如图17所示的单应矩阵。通过单应变换即可实现倾斜校正，即将原始图像对齐到期望的孔洞水平排布的图像上。

图16 霍夫检测直线选取

图17 单应矩阵

校正前后的图像见图18，其中白色的标记点对应校正前的孔洞位置，红色的标记点为校正后的孔洞位置。对于原本向下倾斜瓦楞纸区域中的孔洞校正后均往上移动，同时从右向左孔洞上移幅度逐渐增大。即相当于绕着原本白色直线的左端点进行了相应角度的顺时针旋转，符合预期。对于向上倾斜瓦楞纸区域中的孔洞校正后孔洞均往下移动，越往左下移幅度越大。可以得出结论校正后瓦楞纸叠层中所有孔洞点都趋于了水平分布，此时沿着水平方向对孔洞进行投影，可以避免纸张倾斜问题带来的干扰。根据单应变换的基本原理，理论上提供的匹配点数目越多也即选取的霍夫直线数目越多，单应变换的结果也就更加准确。如何在图像的不同区域选取合适的霍夫直线检测结果仍需要进行更多研究，如果所提供的匹配点全部集中在一小块区域，单应变换的结果很难对不同区域中的倾斜情况进行校正，目前采用的策略是在图像中尽量分散地去选择霍夫检测结果，使得所提供的匹配点尽可能地反映全局信息。对目前已有的图片，不进行倾斜校正也能取得较为准确的结果，所以该校正方法的效果，仍有待在更有针对性、倾斜幅度更大的图片上进行验证。

3 结果与分析

基于孔洞检测的计数算法和基于直线的计数方法相比，一个重要优势是孔洞和瓦楞纸薄片有严格的对应关系，而实际场景下直线和单张瓦楞纸薄片间通常没有较好的对应关系，如图19a中第3张瓦楞纸处发生了明显的变形，通过自适应阈值和形态学操作后，该区域一共检测出4条线状目标，在不依据原图进行判断的情况下，很容易误认为4条线状目标共对应着3张瓦楞纸板，而实际该区域只有一张变形的瓦楞纸板。

图18 倾斜校正结果

图19 纸张变形区域线状检测结果

对于基于孔洞检测的计数方法来说，每排孔洞只可能唯一对应一张瓦楞纸板。所提出的算法在图19纸张变形处检测的结果见图20，孔洞检测相比于直线检测有较明显的优势。

图20 纸张变形区域孔洞检测结果

已有孔洞检测算法均采用在二值图像上进行连通域检测的方法来提取孔洞，而在实际应用中低对比度的图像上二值化很难取得较好的效果，从而进一步影响后续孔洞提取的结果。图21c为自适应阈值分割的结果，图21d为利用连通域检测对孔洞提取的结果，可以发现有部分孔洞发生了联结，同时检测结果中有大量的噪声干扰，楞边和孔洞很容易被判断为属于同一个连通域；图21e为文中提出的孔洞增强算法的效果，该算法可直接在灰度图像上进行孔洞提取，无需进行二值化的操作，在低对比度区域也能较好地提取出孔洞。同时检测结果中只会对孔洞区域进行增强，不会像连通域检测算法一样引入其他非孔洞区域的噪声干扰。

为进一步验证算法在实际工作场景下的通用性与准确性，将计数算法在树莓派上进行编译，并导入一台手持式设备，在实际的工作场景下进行测试，对单楞型的E、B、C和双楞型的BC、BE、AB分别进行了测试。其中BE楞型的瓦楞纸叠层因为摆放过久，出现了孔洞不清晰的情况；BC楞型的瓦楞纸叠层部分孔洞因为受力不均而明显小于标准的孔洞；B楞型的瓦楞纸叠层有纸张倾斜和成像不够清晰等问题。测试结果表明该算法有很强的鲁棒性，在上述问题的干扰下仍能准确得出计数结果。每种楞型的瓦楞纸叠层中用线条标记出了每张瓦楞纸，见图22。对计数结果的统计结果见表1。

图21 孔洞检测方法对比

表1 手持设备1计数结果

Tab.1 Counting result of hand-held device 1

4 结语

文中展示了一种手持式瓦楞纸计数系统的硬件结构以及对应的机器视觉计数算法。现阶段很多瓦楞纸计数算法仍停留在实验室算法仿真阶段，无法在复杂的工业场景下正常运行。该研究的主要贡献有：利用低成本的面阵相机，不依赖额外的机械结构，结合孔洞检测的机器视觉算法，拍摄单张图片即可对整个瓦楞纸叠层进行精确计数，计数效率较高；多尺度的解决方案，能够对各种单楞型和组合楞型的瓦楞纸进行计数；手持式设备灵活便携，应用场景广泛。

[1] 李莉. 瓦楞纸半年度分析——上半年呈“N”型走势 下半年预期偏强[J]. 中华纸业, 2021, 42(15): 28-29.

LI Li. Semi-annual Analysis of Corrugated Paper: "N" Trend in the First Half of the Second Half is Expected to Be Stronger[J]. China Paper, 2021, 42(15): 28-29.

[2] 刘翠翠, 杨涛. 机器视觉在智能制造中的应用与产业发展[J]. 机床与液压, 2021, 49(11): 172-178.

LIU Cui-cui, YANG Tao. Application and Industrial Development of Machine Vision in Intelligent Manufacturing[J]. Machine Tool & Hydraulics, 2021, 49(11): 172-178.

[3] 邹炳华. 一种瓦楞纸生产的纸张高度测量系统: 中国, 110360936A[P]. 2019–10–22.

ZOU Bing-hua. A Paper Height Measuring System for Production of Corrugated Paper: China, 110360936A[P]. 2019-10-22.

[4] Suppitaksakul C, Rattakorn M. Machine Vision System for Counting the Number of Corrugated Cardboard[C]2014 International Electrical Engineering Congress (iEECON), Chonburi, Thailand, 2014: 1-4.

[5] Suzuki S, be K. Topological Structural Analysis of Digitized Binary Images by Border Following[J]. Computer Vision, Graphics, and Image Processing, 1985, 30(1): 32–46.

[6] 黄丹平, 廖世鹏, 于少东, 等. 基于机器视觉瓦楞纸板自动计数系统研究[J]. 机械工程学报, 2017, 53(10): 79-86.

HUANG Dan-ping, LIAO Shi-peng, YU Shao-dong, et al. Research on Automatic Counting System Corrugated Paper Board Based on Machine Vision[J]. Journal of Mechanical Engineering, 2017, 53(10): 79-86.

[7] 杨宪强, 于兴虎, 刘伟华, 等. 一种基于神经网络的瓦楞纸检测算法: 中国, 109671074A[P]. 2019–04–23.

YANG Xian-qiang, YU Xing-hu, LIU Wei-hua, et al. A Detection Algorithm for Corrugated Paper Based on Neural Network: China, 109671074A[P]. 2019-04-23.

[8] 张堃, 韩宇, 徐子洋, 等. 一种基于深度学习的瓦楞纸堆叠层数计数方法: 中国, 111862122A[P]. 2020–10–30.

ZHANG Kun, HAN Yu, XU Zi-yang, et al. A Count Method for Stacking Layers of Corrugated Paper Based on Depth Study: China, 111862122A[P]. 2020-10-30.

[9] ZHU Hui, Chan F H Y, Lam F K. Image Contrast Enhancement by Constrained Local Histogram Equalization[J]. Computer Vision and Image Understanding, 1999, 73(2): 281-290.

[10] ZHANG Zhi-hao, ZHU Peng-bo, YANG Xian-qiang. A Counting Method for Stacked Corrugated Board Based on Autocorrelation[C]// 2018 37th Chinese Control Conference (CCC), Wuhan, 2018: 9379-9382.

[11] 杨宪强, 卫作龙, 张智浩, 等. 一种基于图像轮廓提取与聚类的瓦楞纸智能检测方法: 中国, 109658404A[P]. 2019.

YANG Xian-qiang, WEI Zuo-long, ZHANG Zhi-hao, et al. An Intelligent Detection Method for Corrugated Paper Based on Extraction and Aggregation of Picture Contour: China, 109658404A[P]. 2019.

[12] LIU Jia-min, White J M, Summers R M. Automated Detection of Blob Structures by Hessian Analysis and Object Scale[C]// 2010 IEEE International Conference on Image Processing, Hong Kong, 2010: 841-844.

[13] Štepán-Buksakowska I L, Accurso J M, Diehn F E. Computer-Aided Diagnosis Improves Detection of Small Intracranial Aneurysms on MRA in a Clinical Setting[J]. American Journal of Neuroradiology, 2014, 35(10): 1897-1902.

[14] Jerman T, Pernus F, Likar B. Blob Enhancement and Visualization for Improved Intracranial Aneurysm Detection[J]. IEEE Transactions on Visualization and Computer Graphics, 2016, 22(6): 1705-1717.

[15] Frangi A F, Niessen W J, Vincken K L, et al. Multiscale Vessel Enhancement Filtering[C]// International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer Berlin Heidelberg, 1998: 130-137.

Hand-held Corrugated Cardboard Counting System Based on Machine Vision

XIA Li-yuan1, WANG Pei-long1, ZHAO Hong2, XIAO Chang-yan1, LI Shu-tao1

(1. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China;2. College of Aerospace Science Engineering, National University of Defense Technology, Changsha 410073, China)

The work aims to count the corrugated cardboard accurately. A hand-held corrugated cardboard counting system based on machine vision was proposed and the hardware structure and application scenario of the system were introduced. The blob enhancement algorithm and the blob projection strategy based on slope correction were adopted and compared with the existing counting algorithms for analysis. Finally, counting experiments were carried out on corrugated cardboard laminates with different shapes, and the robustness of the proposed algorithm was further verified. The existing corrugated cardboards with different shapes were tested for many times, and the accuracy of the proposed counting system reached 99%. In the actual working scenario, a large number of tests show that the system can accurately count corrugated cardboard laminates.

corrugated cardboard laminates; machine vision; Hessian matrix; blob test

TB487.1；TP29

A

1001-3563(2022)15-0001-12

10.19554/j.cnki.1001-3563.2022.15.001

2022–07–18

夏立元（1998—），男，湖南大学硕士生，主攻计算机视觉。

肖昌炎（1972—），男，博士，湖南大学教授，主要研究方向为机器视觉与机器人技术。

责任编辑：曾钰婵