基于“货到人”拣选系统的动态货位分配研究

张雪，周丽，路雪鹏，尚娇

基于“货到人”拣选系统的动态货位分配研究

张雪，周丽，路雪鹏，尚娇

（北京物资学院 信息学院，北京 101149）

为了提高“货到人”拣选系统的订单拣选效率，研究了电商仓库货位初始存储状态为非空情况下的商品货位分配问题。考虑货架上现存商品信息、仓库空余货位数、待补货商品和新收入商品信息，提出基于商品关联度的分散存储策略，以极大化货架上所有存储商品的关联度之和为目标构建商品上架与下架的动态货位分配数学模型，并设计贪婪算法，再采用改进粒子群算法对贪婪算法得到的结果进行优化。基于商品关联度的分散存储策略可以减少货架平均搬运次数29.32%左右。与随机分配策略相比，文中提出的货位分配策略能够有效提升整个电商仓储中心的拣选速度。

货到人；货位分配；整数规划模型；贪婪算法；粒子群算法

在我国互联网技术不断发展，各大电商平台支付安全系统不断升级的背景下，电子商务得以迅速发展，并且由传统的“人到货”订单拣选模式逐渐向基于自动引导车（Automated Guided Vehicle, AGV）的“货到人”订单拣选模式转变。具有成本效益的AGV物流搬运方案实现了“货到人”的分拣，为电商仓储带来了革命性变革。与“人到货”拣选系统类似，“货到人”拣选系统也存在一些亟须解决的问题，包括货位分配优化、订单处理[1-2]、AGV小车任务分配及调度[3-4]、路径规划[5-6]等问题。在提高仓储配送中心拣选效率的方法中，科学的货位分配方法是提高拣选效率的基础，也是一种战略上的决策，比订单分批、优化拣选路径等方法减少了AGV搬运货架的次数和距离。

货位分配是指企业依据商品的特征、需求以及其他相关变动因素，对商品存储的位置进行动态的调整[7]。“人到货”拣选系统有关货位分配问题的研究成果已经相当成熟，主要是通过货位存储策略[8-10]、商品关联关系分析[11-12]和商品聚类分析[13-14]等3个方面进行优化。“人到货”拣选系统中货架不可移动，对订单拣选效率影响最大的是拣选工作人员，而“货到人”拣选系统中，货架具有可移动性，主要是利用AGV小车搬运货架，因此“人到货”拣选系统的相关研究成果不能直接应用于“货到人”拣选系统。

在“货到人”拣选系统的商品货位分配问题中，通常需要计算商品之间的关联度，并以此作为依据，将关联度高的商品存储在同一个货架上。袁瑞萍等[15]建立了极大化每个货架上商品之间的关联度平均值的数学模型，并通过仿真进行求解。Kim等[16]考虑一种商品可以放在多个货架上的情况，设计了一种优化启发式算法求解基于商品关联度的货位分配问题。包菊芳等[17]采用FP–Growth算法计算商品之间的关联度，并将相关度高的商品存储在同一个货架上，与随机货位分配策略相比，能够有效减少货架搬运次数。Mirzaei等[18]基于历史订单中的商品周转率和关联性，采用集成集群分配策略，并设计启发式算法进行求解。也有的学者从其他角度出发对商品存储位置进行优化。Onal等[19]基于爆炸存储的商品货位分配策略，构建了商品货位分配的排队论模型。Lamballais等[20]构建了单行和多行订单的排队网络模型，评估不同存储策略下的订单最大吞吐量、平均拣选周期和机器人利用率3种指标。

学者们在研究“货到人”拣选系统的商品货位分配时，大部分考虑的是货架的初始状态是空的，即集中于研究静态的商品货位分配问题，但实际上电商仓储中心货架上是存放商品的，需要定期的对商品进行补货或者下架某些滞销商品，这是一个动态的货位分配问题，并且一种商品应该存放在多个货架上，而关于这些方面的研究较少，因此需要对一品多位的动态货位分配问题进行展开研究。

1 问题描述

如图1所示，“货到人”拣选系统按仓库区域的功能可分为商品补货区、货架存储区、商品拣货区、AGV充电区和AGV等待区。在接到订单拣选指令后，由AGV小车和工作人员合作完成订单的拣选工作。

在“货到人”拣选系统中研究商品的货位分配问题时，需要优先考虑将具有关联性的商品存储在同一个货架上，以此减少AGV小车搬运货架的次数。此外，在仓库总货位数一定，货架上目前存储的商品信息已知情况下，需要考虑仓库经过一个订单拣选周期后，货架上的部分商品会出现缺货状态，以及可能会有新收入的商品需要存储在货架上的情况，因此需要对货架上缺货的商品及新收入的商品进行补货和上架操作。

根据电商订单呈小批量多批次的特点，提出了基于商品关联度的分散存储策略，即首先采用商品分散存储策略，即同一种商品可以存储在多个货架上，但不能存储在同一个货架上的策略，使同一个货架上存储的商品种类达到最多，从而增加商品不同拣选的可能性。其次，通过极大化同一货架上商品间的关联度之和，获取商品在货架上的最佳存储位置，达到有效减少货架搬运次数，提高订单拣选效率的目的。

整体的货位分配操作示例见图2。货架的初始存储状态已知，数字1—9代表的是商品种类编号，数字0代表的是空货位，其中，商品4、商品8和商品9是待补货商品，根据待拣选订单信息，先将商品7进行下架操作，空出额外需要的货位数，再经过关联度计算，分别将商品4、商品8和商品9分配在对应的货架上。

图2 商品货位分配过程

2 数学模型构建

2.1 模型假设

在构建商品动态货位分配数学模型过程中遵循以下基本假设条件。

1）在拣选过程中每个订单单独拣选。

2）在商品动态货位分配之前，下一阶段的拣选订单商品信息已知。

3）每个订单中包含一种或多种不同的商品。

4）不考虑商品的体积以及大小，即一个货位可以容纳任意一种商品。

5）每种商品可以存储在多个货架上。

6）一个货位只能分配一种商品。

7）不考虑货架上现存商品的下架成本。

8）每个订单中商品只订购一件，每个货位上存储的商品数量充足。

2.2 符号说明

2.2.1 名词解释

货架上现存商品表示目前存储在货架上的原有商品集合，仓库原有待补货商品表示有补货需求的原有商品集合，新收入待上架商品表示历史订单商品集合中没有的商品种类。

2.2.2 参数符号说明

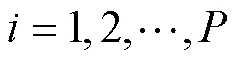
2.2.3 变量符号说明

2.3 模型构建

2.3.1 各商品之间的关联度计算

1）仓库原有待补货商品之间的关联度为：

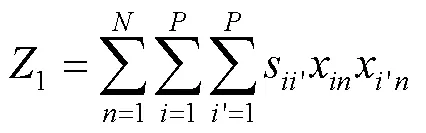
2）新收入待上架商品与新收入待上架商品之间的关联度为：

3）仓库原有待补货商品与新收入待上架商品之间的关联度为：

4）仓库原有待补货商品与货架上现存商品之间的关联度为：

5）新收入待上架商品与货架上现存商品之间的关联度为：

2.3.2 构建模型

在以上假设条件和参数下，建立商品动态货位分配模型。

目标函数：

约束条件：

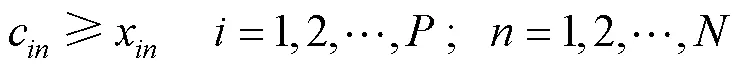
上述模型中，目标函数表示极大化货架上所有存放商品的关联度之和；约束条件（1）表示一个货架上存放的待补货商品和新收入待上架商品的种类数之和不超过这个货架上的空余货位数；约束条件（2）表示一个货架上待补货商品和新收入待上架商品的实际分配货位数之和不超过这个货架上的空余货位数；约束条件（3）表示待补货商品和新收入待上架商品在所有货架上的实际分配货位个数之和等于待补货商品和新收入待上架需要的货位分配个数之和；约束条件（4）表示当待补货商品被分配到一个货架上时，该货架要给该商品分配货位；约束条件（5）表示当新收入待上架商品被分配到一个货架上时，该货架要给该商品分配货位；约束条件（6）表示货架上现存商品中需要下架的总货位数不少于待补货商品与新收入待上架商品实际分配的货位数之和减去仓库的总空余货位数；约束条件（7）表示减去下架商品货位数后的货架上现存商品的货位数与待补货商品和新收入待上架商品的实际分配货位数之和等于仓库的总货位数；约束条件（8）和约束条件（9）为变量取值约束。

在“货到人”拣选系统中，AGV小车在接收任务后，通过举升、导航和行驶等系统，以直线运动（东南西北4个方向）或原地旋转运动的方式将目标货架搬运至拣选台或补货台。整个AGV小车拣选操作均由订单信息控制系统进行指令下达，并确认货架存储区里目前所存储待拣选订单里所需商品的数量以及存储的货位，因此需要在订单信息控制系统中设计一个统计与安排商品货位的算法，使AGV小车能够快速地完成货架搬运任务。

3 求解算法设计

3.1 贪婪算法

文中建立的商品动态货位分配模型是一个非线性混合整数规划模型，当待拣选订单和商品种类数量较多时，在短时间内很难直接获得模型的精确最优解，因此，需要针对文中提出的货位分配问题和模型特点，设计能够快速求解该模型的启发式算法。文中设计的启发式算法如下所述。

第1阶段主要采用贪婪算法得到初始的商品货位分配结果。

输入：历史订单数据，仓库内待补货商品的种类数及对应的货位数，新收入待上架商品的种类数及对应的货位数，货架上现存商品初始的货位存储状态。

1）统计所有货架上现存商品的种类及其所占的货位数，历史订单数据中包含的货架上现存商品的种类信息，将订单中不包含的货架上现存商品种类视为滞销商品，下架对应货位数。

2）找出全部有空位的货架，将每个货架上现存商品视为一个集合，根据历史订单信息和关联性计算公式，求解所有待补货商品与每个货架上现存商品集合的关联度之和，所有新收入待上架商品与每个货架上现存商品集合的关联度之和，并将所有的关联度和进行降序排列。

3）从降序排列中找到与货架上现存商品集合关联度和最大的商品，判断该货架上是否只有一个空货位，如果只有一个空货位，则进入步骤4，否则进入步骤5。

4）判断该商品是否只需要分配一个货位，如果只需要分配一个货位，则将该商品分配在对应的货架上，更新待分配的商品集合；如果需要分配2个及以上的货位，则先存放1个货位在对应货架上，并将该商品视作货架上现存商品，更新待分配的商品集合和货架上现存商品集合，进入步骤2。

5）如果该货架上有2个及以上的货位，判断该货架上是否有商品存储，如果有商品存储，找到与货架上现存商品集合关联度和最大的商品存放在该货架上，进入步骤4，否则进入步骤6。

6）如果该货架上5层货位均为空，计算所有剩余未被分配的仓库原有待补货商品和新收入商品之间的关联度值，将关联度高的5种商品分配在该货架上，更新待分配的商品集合和货架上现存商品集合，判断仓库内所有待上架商品是否全部分配完成，如果全部完成，则结束计算，否则进入步骤2。

输出：商品补货以及新收入商品上架后的货架上存放的商品信息。

3.2 粒子群算法

第2阶段主要是采用粒子群算法对第1阶段贪婪算法得到的货位分配结果进行优化。该算法不需要像其他优化算法那样，例如遗传算法，需要对个体进行选择操作、交叉操作和变异操作等，因此减少了复杂的遗传操作。

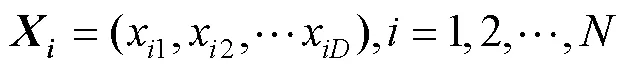
粒子根据以式（10）来更新自身的速度和位置。

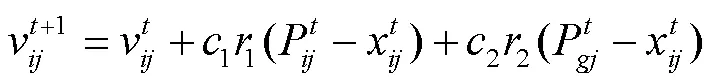
为了使粒子在不同的进化阶段拥有不同的搜索能力，文中引入了动态惯性权重。为设定一个变化区间，即在算法开始时，赋予惯性权重一个较大的正值，在算法结束时，赋予惯性权重一个较小的正值。

动态惯性权重值目前采用最多的是线性递减惯性权重：

式（14）是一种经验做法，文中在后期对模型进行求解时首先与其他2种惯性群众选择方法进行对比，从而选择最优的惯性权重：

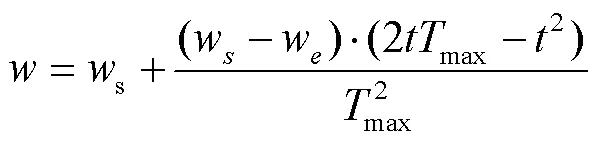
该阶段算法的具体步骤如下。

输入：第1阶段贪婪算法得到的初始货位分配结果，即每个货架上存放的具体商品信息。

1）根据第1阶段的货位分配结果初始化粒子群，设定种群规模、最大迭代次数、每个粒子的速度和位置等。

2）计算每个粒子的适应度值。

5）计算动态惯性权重值，更新迭代每个粒子的位置和速度。

6）判断是否完成迭代次数，如果完成则结束计算，输出最优的可行解，否则返回步骤2继续计算。

输出：优化后的商品货位分配结果。

文中商品动态货位分配算法总流程见图3。

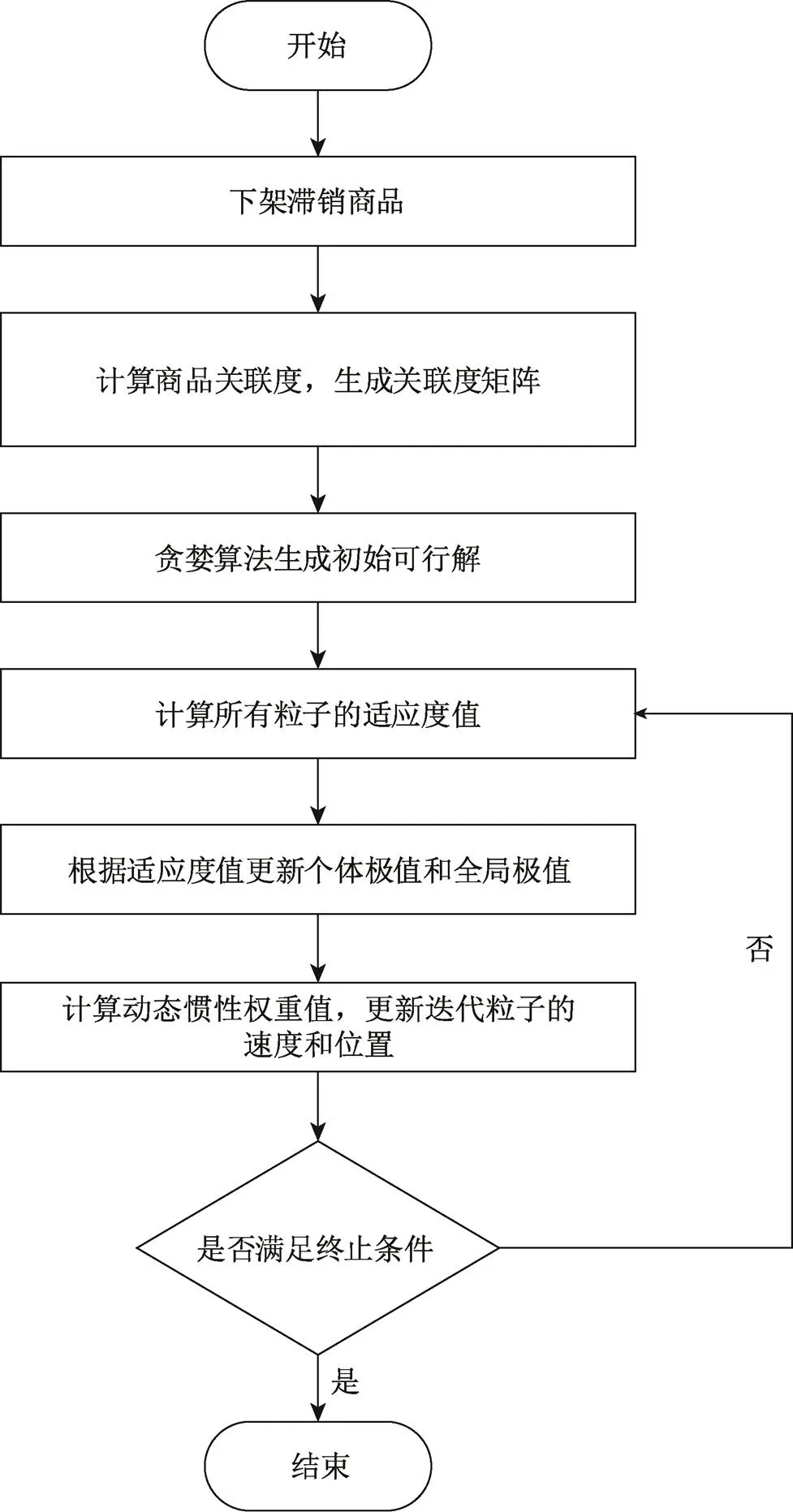
图3 商品动态货位分配算法总流程

4 模拟计算与分析

4.1 算例描述

某个电商仓库中包含30个货架，每个货架分成5层，共存储55种商品，在仓库运行一段时间后，仓库某些货位为空状态，即货位上没有商品存储。现仓库接到300个订单需要拣选，每个订单里包含的商品种类不超过10种，待拣选订单见表1，其中包括10种（商品编号为56—65）之前进行预售的商品。根据待拣选订单，发现仓库现有存储的55种商品中有商品需要进行补货，以及新收入的商品需要存储到货架上，待补货商品和新收入的商品的种类和所需要的货位数见表2。目前仓库的空余货位不足以存储全部的待补货商品和新收入商品，在考虑每个订单单独拣选的情况下，需要将全部待补货商品和新收入商品分配在货架上，并且要达到订单总拣选效率最高。

表1 300个待拣选订单信息

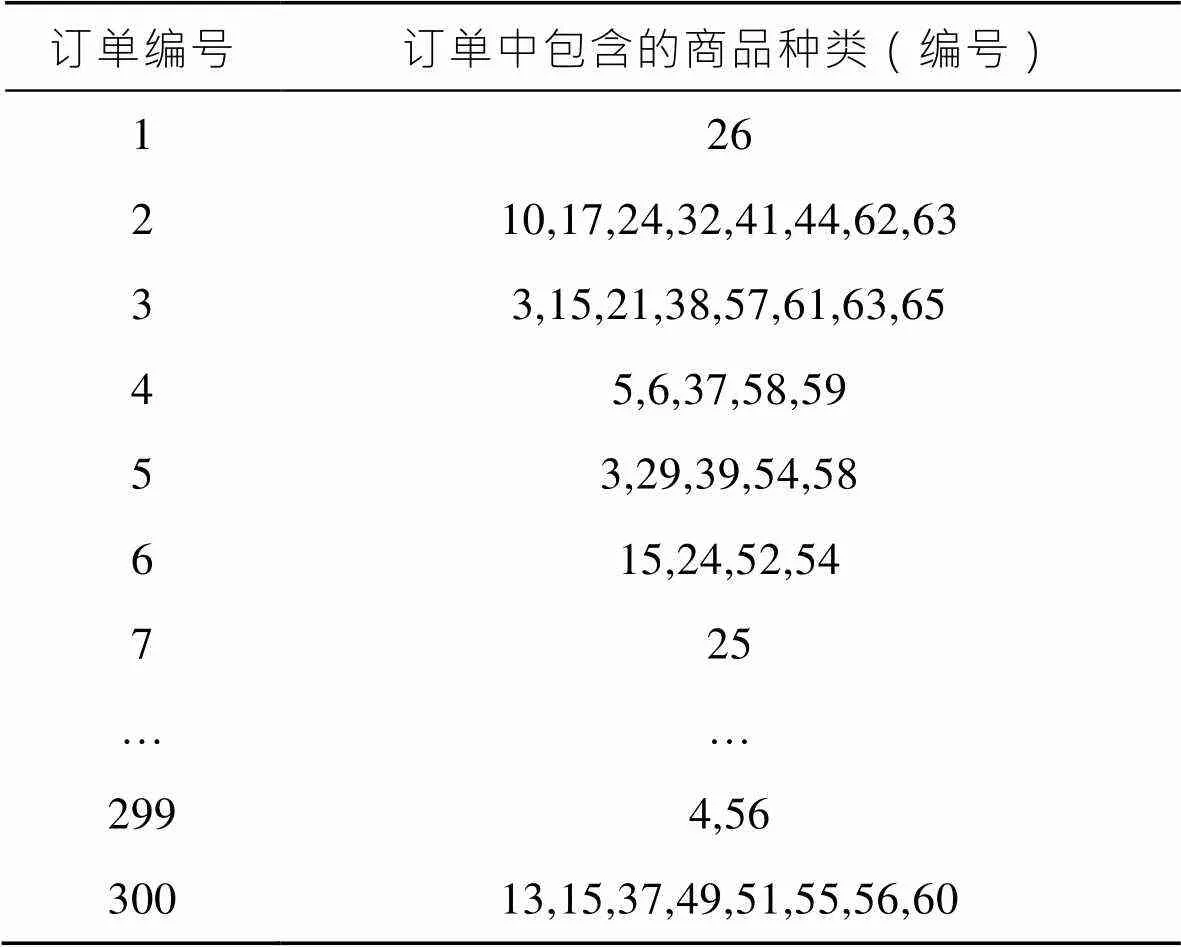
Tab.1 Information of 300 orders to be picked

表2 待补货商品及新收入商品所需货位数

Tab.2 Number of allocations for goods to be replenished and new incoming goods

4.2 结果分析

根据前文的描述以及文中设计的货位分配策略和算法，在Intel(R) Core(TM) i3–4160 CPU @ 3.60 GHz 3.60 GHz处理器，Matlab R2019(a)编程环境下得到货位法分配结果。其中，对式（14）、式（15）、式（16）不同的惯性权重选择进行了研究，最终选择式（15）作为文中的惯性权重计算公式。

首先根据历史订单计算55种仓库现有商品之间的关联度，同时根据待拣选订单计算所有商品之间的关联度，并将此关联度矩阵累计加入到历史订单关联度矩阵中，最终的商品关联度计算结果见表3。

经过算法的不断迭代与更新，得到各分配策略的货位分配结果。贪婪算法经过0.219 s得到的初始货位分配结果见表4。粒子群算法对初始货位分配结果进行优化后得到的货位分配结果见表5，其算法收敛曲线见图4。将全部待补货商品和新收入商品随机的分配在货架上，得到的货位分配结果见表6。

表3 商品关联度计算结果

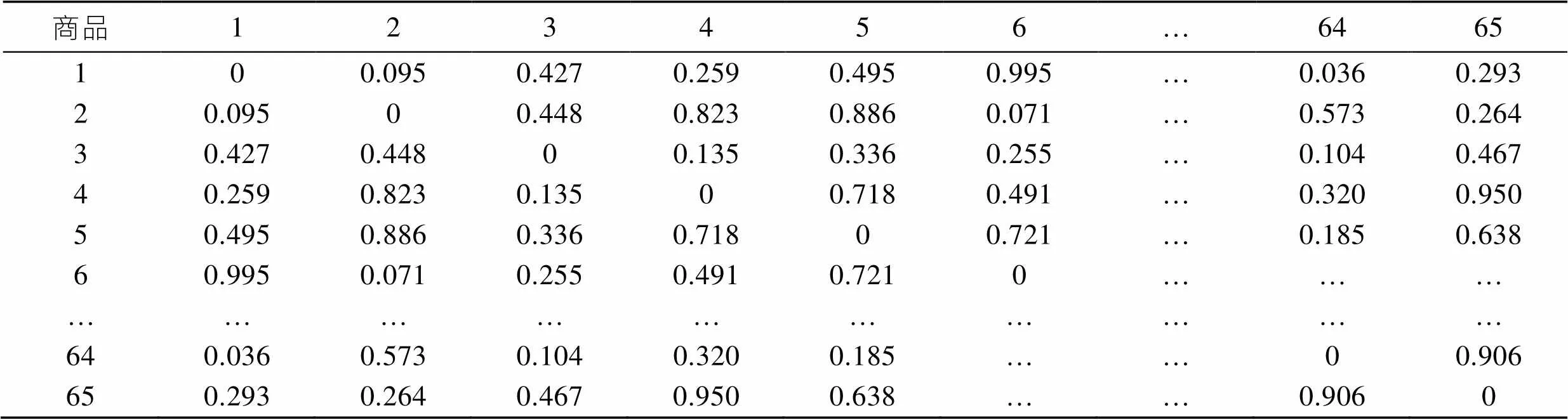
Tab.3 Goods relevance calculation result

表4 贪婪算法得到的初始货位分配结果

Tab.4 Initial goods allocation obtained by the greedy algorithm

注：（）里表示的是货架的初始存储状态，包含下架的商品种类。

表5 粒子群算法优化后得到的货位分配结果

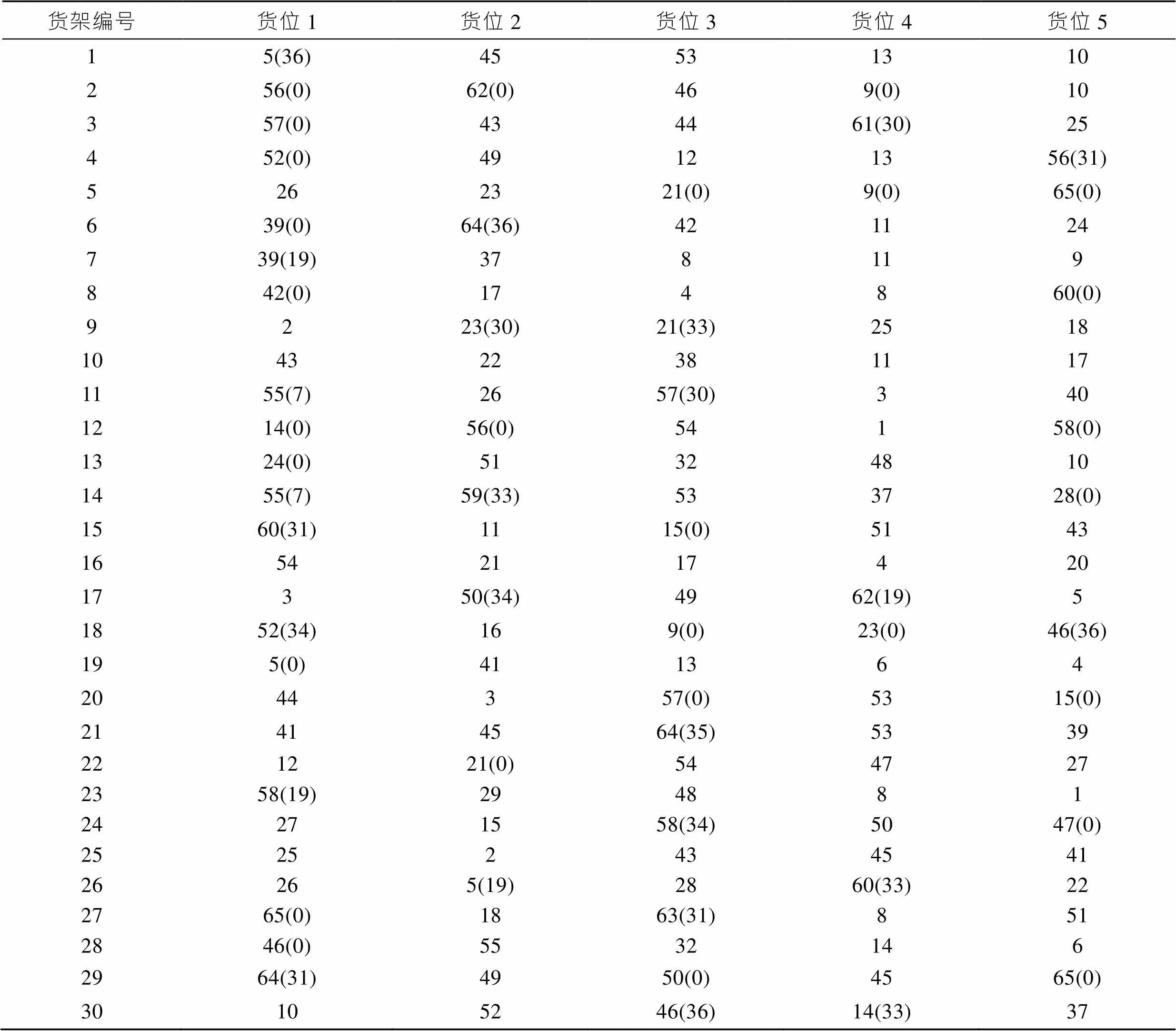
Tab.5 Goods allocation obtained after optimization by particle swarm algorithm

注：（）里表示的是货架的初始存储状态，包含下架的商品种类。

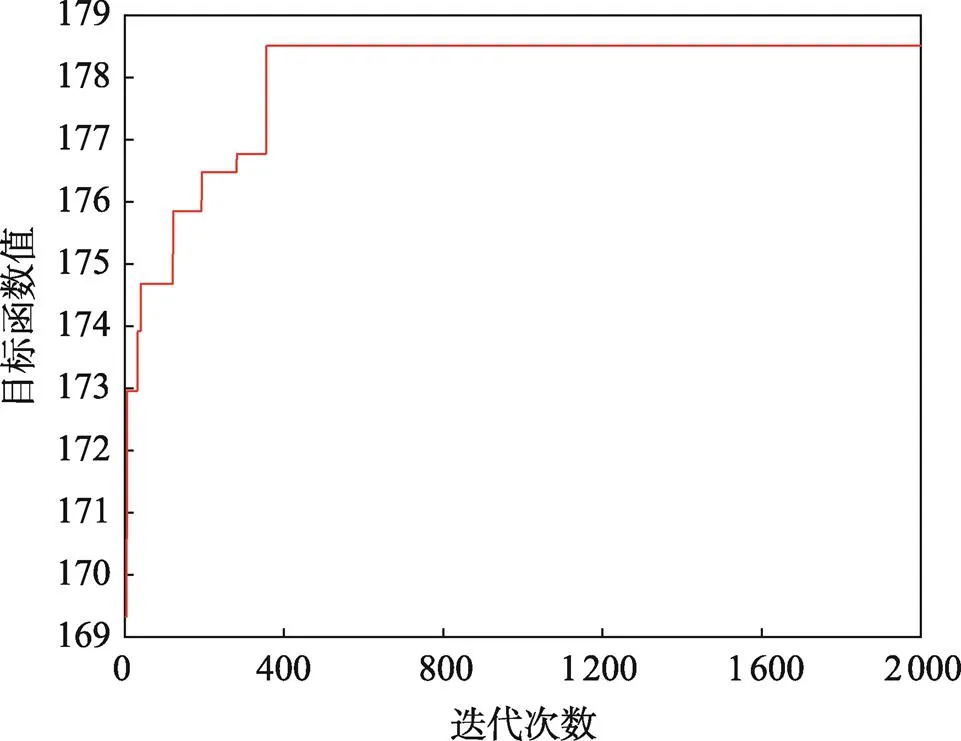
图4 粒子群算法收敛曲线

在完成同一批300个订单拣选时，文中提出的基于商品关联度的分散存储策略和随机存储策略的结果对比见表7。基于商品关联度的分散存储策略需要搬运货架1 166次，随机分配策略需要搬运货架1 651次，将2种货位分配策略进行对比，文中的货位分配策略可有效地将货架的搬运次数降低29.38%。同时，文中货位分配策略得到的所有货架上商品的关联度之和比随机分配策略得到的所有货架上商品的关联度之和提高了37.94%。

为了证明文中提出的算法在求解货位分配模型结果时的稳定性，在订单数为300和每个货架的货位数固定（5）的情况下，设计不同数量的补货商品总数、新收入商品总数和不同规模的货架数。文中策略与随机分配策略的货架搬运次数进行了对比，对比结果见表8。

表6 随机分配得到的货位分配结果

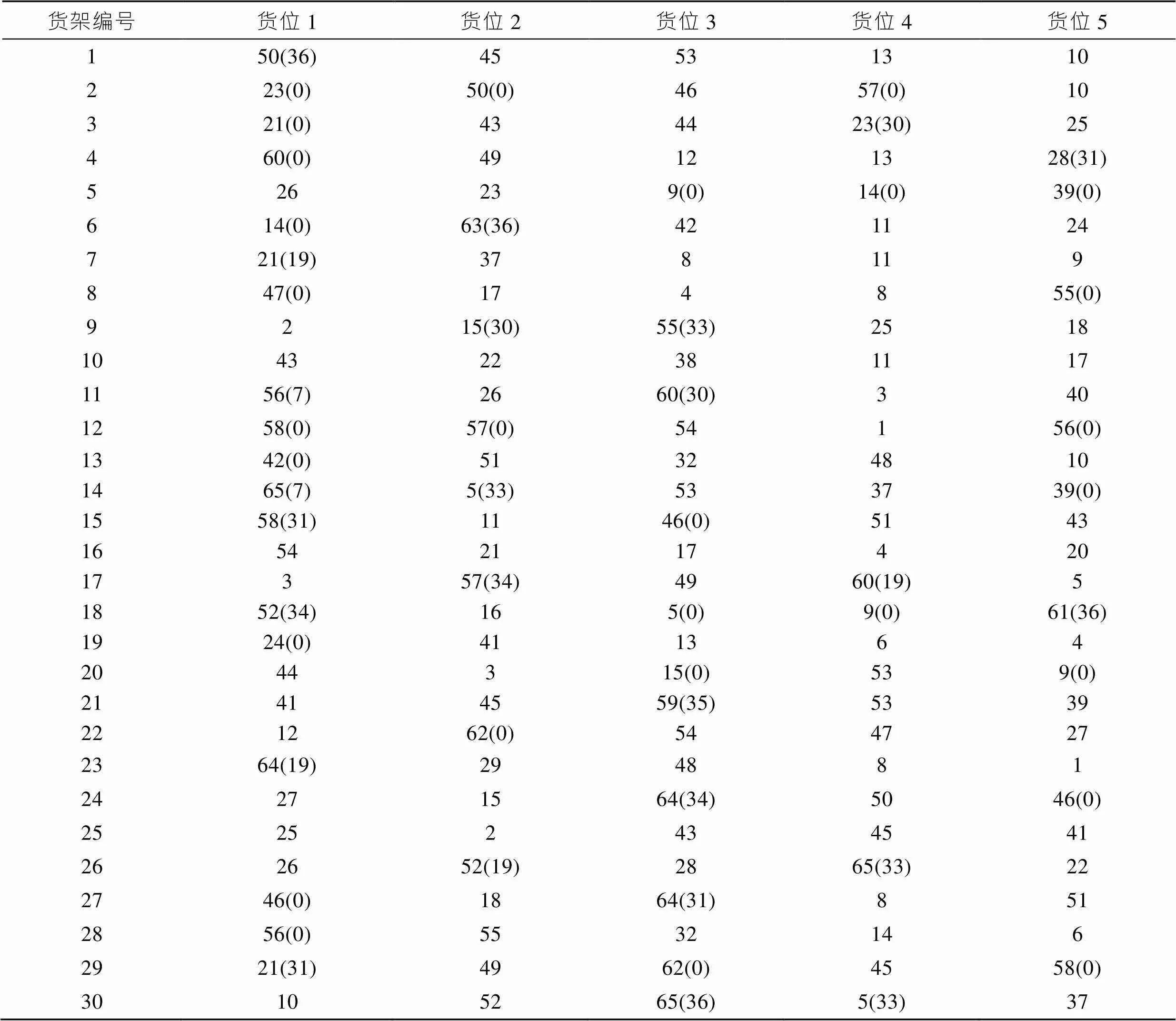
Tab.6 Goods allocation obtained by random distribution

注：（）里表示的是货架的初始存储状态，包含下架的商品种类。

表7 2种货位分配策略结果对比

Tab.7 Comparison of 2 goods allocation strategies

表8 不同规模搬运货架次数结果对比

Tab.8 Comparison of handling number of shelves of different scales

由表8可知，与随机分配策略相比，文中提出的基于商品关联度的分散存储策略的货架搬运次数平均降低了29.32%，由此证明了文中提出的分配策略及算法具有稳定性和可行性。

5 结语

近年来，随着电商的快速发展，电商企业为了提高订单的拣选作业和配送作业效率，已经开始逐渐采用“货到人”拣选系统。文中对所有商品之间的关联度进行计算，根据一种商品可以存储在多个货架上、仓库内原有待补货商品所需要的货位数、新收入待上架商品所需要的货位数等约束条件构建数学模型，设计贪婪算法和粒子群算法进行求解，并通过仿真进行算例验证，结果表明，文中提出的货位分配策略可以明显减少货架平均搬运次数。

在研究“货到人”拣选系统货位分配问题时，文中以滞销商品下架的货位总数超过待补货商品和新收入商品所需额外货位数之和为约束条件，即存在某些商品种类不在待拣选订单中的情况，但从实际角度出发，可能会存在待拣选订单中包含全部商品的情况，同时，文中没有考虑仓库滞销商品的下架成本，因此，在下一步的研究中将着重考虑这2种情况。

[1] YANG X, HUA G, HU L, et al. Joint Optimization of Order Sequencing and Rack Scheduling in the Robotic Mobile Fulfilment System[J]. Computers & Operations Research, 2021, 135: 105467.

[2] BOYSEN N, BRISKORN D, EMDE S. Parts-to-Picker Based 0rder Processing In a Rack-Moving Mobile Robots Environment[J]. European Journal of Operational Research, 2017, 262(2): 550-562.

[3] ROY D, NIGAM S, DE KOSTER R, et al. Robot-Storage Zone Assignment Strategies in Mobile Fulfillment Systems[J]. Transportation Research Part E Logistics and Transportation Review, 2019, 122: 119-142.

[4] SHARMA K, DORIYA R. Coordination of Multi-Robot Path Planning for Warehouse Application Using Smart Approach for Identifying Destinations[J].Intelligent Service Robotics, 2021, 14(2): 313-325.

[5] PAIKRAY H K, DAS P K, PANDA S. Optimal Multi-Robot Path Planning Using Particle Swarm Optimization Algorithm Improved by Sine and Cosine Algorithms[J]. Arabian Journal for Science and Engineering, 2021, 46(4): 3357-3381.

[6] 雷斌, 王菀莹, 赵佳欣. 货位分配优化研究综述[J]. 计算机工程与应用, 2021, 57(1): 48-55.

LEI Bin, WANG Wan-ying, ZHAO Jia-xin. Review of Research on Location Allocation Optimization[J]. Computer Engineering and Applications, 2021, 57(1): 48-55.

[7] BORTOLINI M, FACCIO M, FERRARI E, et al. Design of Diagonal Cross-Aisle Warehouses with Class-Based Storage Assignment Strategy[J]. The International Journal of Advanced Manufacturing Technology, 2019, 100(9): 2521-2536.

[8] ZHOU Li, SUN Li-li, LI Zhao-chan, et al. Study on a Storage Location Strategy Based on Clustering and Association Algorithms[J]. Soft Computing, 2020, 24(8): 5499-5516.

[9] 李阳, 唐磊, 胡俊. 基于遗传算法的航天零件仓库货位优化研究[J]. 制造业自动化, 2020, 42(8): 68-73.

LI Yang, TANG Lei, HU Jun. The Research on Space Parts Warehouse Location Optimization Based on Genetic Slgorithms[J]. Manufacturing Automation, 2020, 42(8): 68-73.

[10] PANG K W, CHAN H L. Data Mining-Based Algorithm for Storage Location Assignment in a Randomised Warehouse[J]. International Journal of Production Research, 2017, 55(14): 4035-4052.

[11] LEE C. A GA-Based Optimisation Model for Big Data Analytics Supporting Anticipatory Shipping in Retail 4.0[J]. International Journal of Production Research, 2016, 55(2): 593-605.

[12] 周亚云, 项前, 余崇贵, 等. 考虑物料需求关联与周转率的仓储货位优化方法[J]. 东华大学学报(自然科学版), 2020, 46(3): 414-420.

ZHOU Ya-yun, XIANG Qian, YU Chong-gui, et al. A Method for Storage Location Optimization Considering Material Demand Correlations and Turnover[J]. Journal of Donghua University (Natural Science), 2020, 46(3): 414-420.

[13] HOLÝ V, SOKOL O, ČERNÝ M. Clustering Retail Products Based on Customer Behaviour[J]. Applied Soft Computing Journal, 2017, 60: 752-762.

[14] NIU J. Intelligent Evaluation Model of E-Commerce Transaction Volume Based on the Combination of K-Means and SOM Algorithms[J]. International Journal of Information and Communication Technology, 2021, 18(2): 189.

[15] 袁瑞萍, 王慧玲, 李俊韬, 等. 基于移动机器人的订单拣选系统货位优化模型和算法研究[J]. 系统科学与数学, 2020, 40(6): 1050-1060.

YUAN Rui-ping, WANG Hui-ling, LI Jun-tao, et al. The Slotting Optimization Model and Algorithm in Robotic Mobile Fulfillment Systems[J]. Journal of Systems Science and Mathematical Sciences, 2020, 40(6): 1050-1060.

[16] KIM H J, PAIS C, SHEN Z J M. Item Assignment Problem in a Robotic Mobile Fulfillment System[J]. IEEE Transactions on Automation Science and Engineering, 2020, 17(4): 1854-1867.

[17] 包菊芳, 王丽. 基于SKU关联度的储位优化问题研究[J]. 数学的实践与认识, 2021, 51(14): 31-40.

[18] BAO Ju-fang, WANG Li. Research on Optimization of Storage Location Based on SKU Correlation[J]. Mathematics in Practice and Theory, 2021, 51(14): 31-40.

[19] MASOUD M, NIMA Z, RENÉ D K. The Impact of Integrated Cluster-Based Storage Allocation on Parts-to-Picker Warehouse Performance[J]. Transportation Research Part E, 2021, 146: 102207.

[20] ONAL S, ZHANG Jing-ran, DAS S. Modelling and Performance Evaluation of Explosive Storage Policies in Internet Fulfilment Warehouses[J]. International Journal of Production Research, 2017, 55(20): 5902-5915.

[21] LAMBALLAIS T, ROY D, DE KOSTER M. Estimating Performance in a Robotic Mobile Fulfillment System[J]. European Journal of Operational Research, 2017, 256(3): 976-990.

Dynamic Allocation Based on “Goods-to-person” Picking System

ZHANG Xue, ZHOU Li, LU Xue-peng, SHANG Jiao

(School of Information, Beijing Wuzi University, Beijing 101149, China)

The work aims to study the goods allocation when the initial storage status of the e-commerce warehouse is not empty, so as to improve the order picking efficiency of the “goods-to-person” picking system. Considering the information of the existing goods on the shelf, the number of vacant goods allocation in the warehouse, the goods to be replenished and the information of the new incoming goods, a decentralized storage strategy based on the degree of goods relevance was proposed to maximize the sum of the relevance of all stored goods on the shelf, thus constructing the mathematical model of dynamic allocation of goods on and off the shelves. Then, a greedy algorithm was designed, and the particle swarm algorithm was improved to optimize the results obtained by the greedy algorithm. The decentralized storage strategy based on the degree of goods relevance could reduce the average number of shelf handling by about 29.32%. Compared with the random allocation strategy, the proposed allocation strategy can effectively improve the picking speed of the entire e-commerce storage center.

“goods-to-person”; goods allocation; integer programming model; greedy algorithm; particle swarm algorithm

F274

A

1001-3563(2022)15-0247-11

10.19554/j.cnki.1001-3563.2022.15.029

2021–11–26

国家自然科学基金（71501015）；北京社科基金重点项目（18GLA009）；北京市长城学者项目（CIT&TCD20170317）

张雪（1994—），女，北京物资学院硕士生，主攻智能物流系统。

周丽（1978—），女，博士，北京物资学院教授，主要研究方向为智能物流系统。

责任编辑：曾钰婵