非均匀张力作用下多层膜结构动力稳定性研究

邵明月，张淼，武吉梅，庆佳娟，王静

非均匀张力作用下多层膜结构动力稳定性研究

邵明月1，张淼1，武吉梅1，庆佳娟2，王静2

（1.西安理工大学 印刷包装与数字媒体学院，西安 710054；2.西安理工大学 机械与精密仪器工程学院，西安 710048）

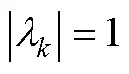
非均匀张力；变速度；多层膜结构；动态稳定性

柔性电子制造通过卷到卷（R2R）方式可以有效控制生产成本、简化生产工艺、有效避免材料浪费，已经成为RFID、薄膜太阳能电池、OLED、印刷电子等领域理想制造技术。从柔性电子制造的生产过程和功能薄膜的制备工艺可以看出，其具有明显的多层化特点。其多层化、多材料特性，常常表现出异于一般结构的复杂力学行为[1]，在生产过程中多层膜结构产生的振动对涂布的均匀性、精准封装等会造成严重影响，降低产品质量。

在R2R柔性电子制造中，料带并不是严格匀速运动的。在涂布、干燥、输送等过程中，料带进行高温镀层时质量的增加、干燥时受到烘箱气体的干扰、收放卷时料卷直径的变化和导向辊转动时的扰动，薄膜的速度通常是变化的，微小的速度扰动都会对印刷电子薄膜产品的质量产生很大的影响。由于导向辊安装不平行也会导致薄膜两端产生非均匀张力，导致涂布层粗糙度发生变化，引起褶皱。因此研究多层膜结构在非均匀拉力作用下变速运动振动特性十分有必要。近年来已经有大量关于轴向运动层合板横向振动及稳定性的研究。赵飞等[2]采用分层理论对复合材料层合板的固有频率和振型进行理论计算。刘金建等[3]利用多尺度法分析了变速运动板的失稳规律。陈立群等[4]用解析和数值方法同时研究了面内变速运动粘弹性板的横向非线性振动，考察了面内运动平均速度、面内运动速度涨落、黏性系数等对稳态响应的影响。Yang等[5]采用多尺度法得到了轴向加速复合材料板的稳定边界。Lu等[6]采用直接多尺度方法，研究了轴向移动的石墨烯增强层合板的动态稳定性。刘金堂等[7]利用Galerkin法与平均法研究了由共振引发的失稳区域。Hatami[8]利用经典板理论研究了平面内力作用下轴向移动对称层合板的自由振动问题。Aydogdu[9]利用高阶剪切变形层合板理论研究了复合材料动力特性。Marynowski等[10]研究了温度对轴向移动多尺度复合材料板自由振动和临界输运速度的影响。Han等[11]用分析薄层结构振动的里兹方法研究了对称叠层斜板的自由振动。关于轴向运动薄膜横向振动及其参数振动也有许多研究成果。侯志勇等[12]利用达朗贝尔原理建立轴向运动薄膜横向振动微分方程，并用微分求积法验证解析解，求出了轴向运动薄膜的稳定区间。武吉梅[13]根据Floquet理论确定了纸带的动力不稳定区域和稳定区域。邵明月[14]研究了非均匀张力下变速膜的振动特性和稳定性。Wu等[15]研究了系统参数对变速膜振动特性和稳定性的影响。卢瑶等[16]研究了变速运动粘弹性硬质薄膜的稳定性，分析了不同参数对运动薄膜稳定区域的影响。

以上研究少见对计及弯曲刚度非均匀拉力下变速多层膜结构的振动分析。文中综合考虑了弯曲刚度及非均匀张力对变速复合膜结构运动稳定区域的影响，根据Floquet理论，得到了运动膜的动态稳定区间并绘制关系曲线分析系统参数对稳定区域的作用规律。

1 动力学模型及振动微分方程的建立

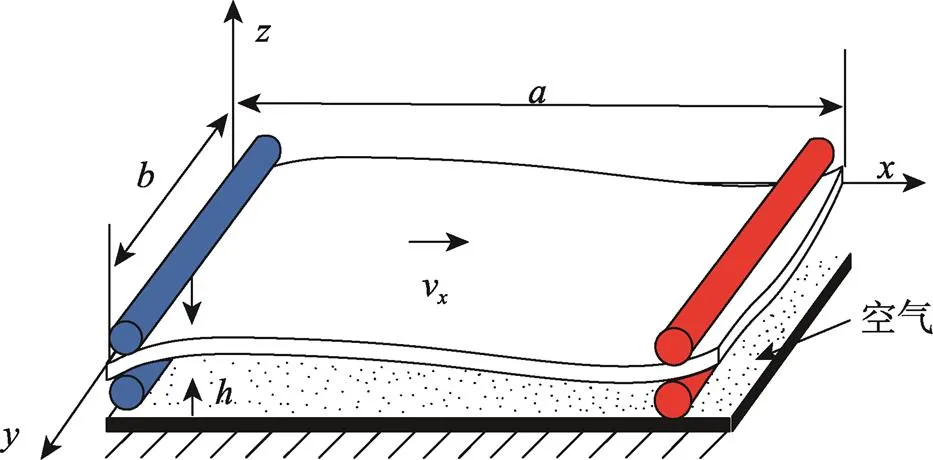
图1 运动多层膜结构动力学模型

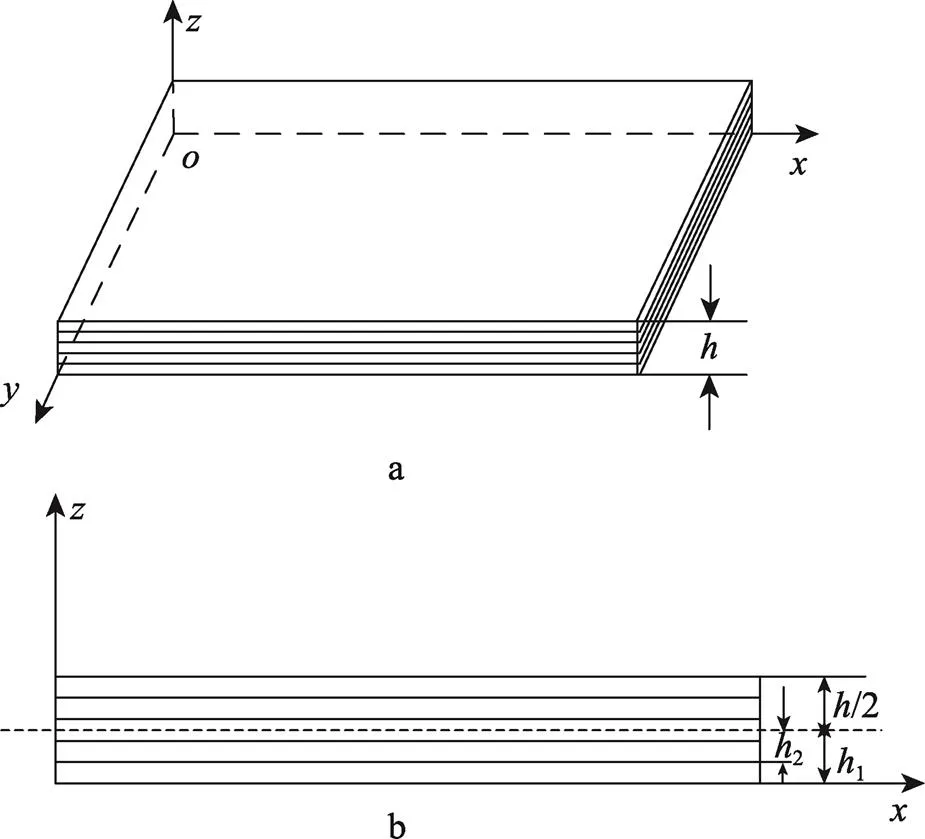
图2 多层膜微观结构理论模型示意图

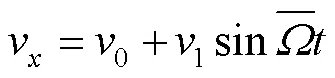
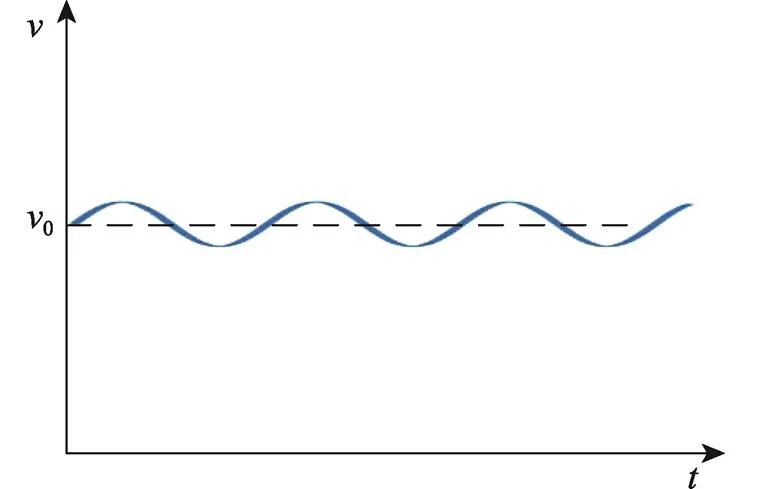
图3 速度变化曲线

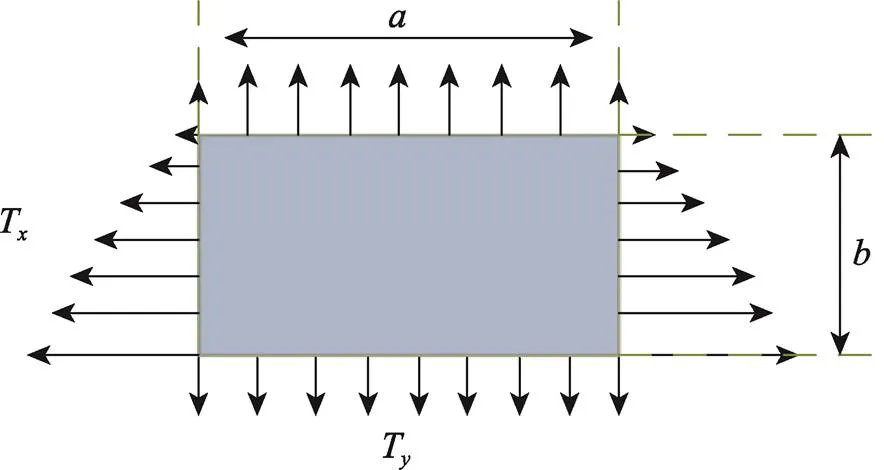
图4 非均匀张力作用示意图

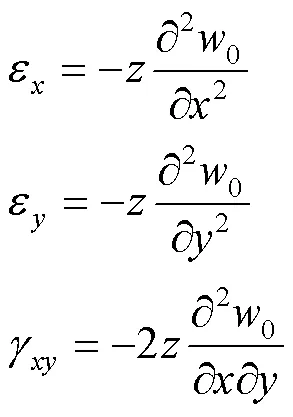
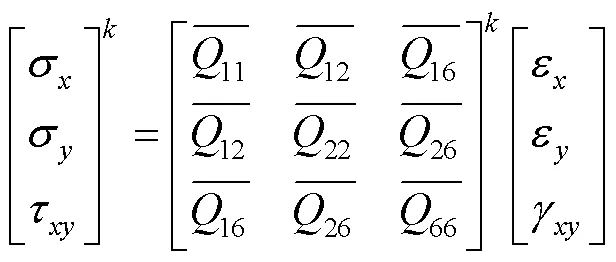
多层膜结构运动时横向振动方向上的速度为[12]：

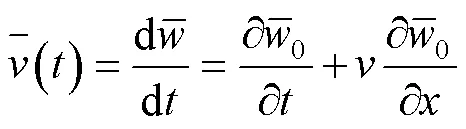
根据Hamilton原理建立多层膜结构的能量方程式：

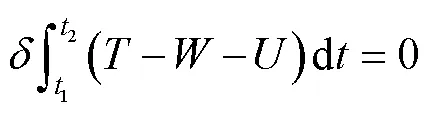
其中：

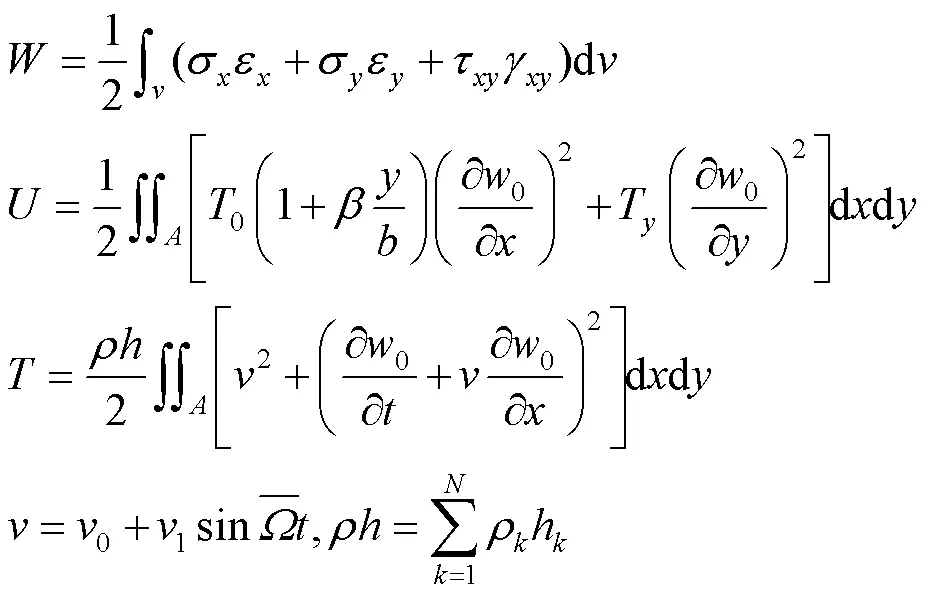
对式（4）进行变分运算得振动微分方程为：

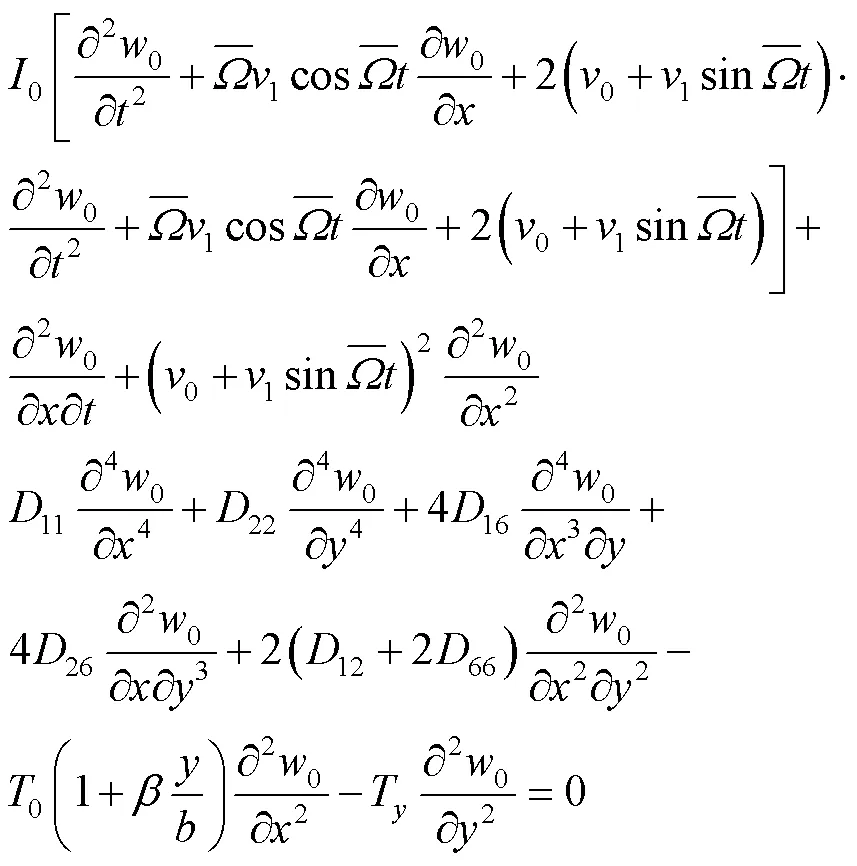
引入无量纲量：

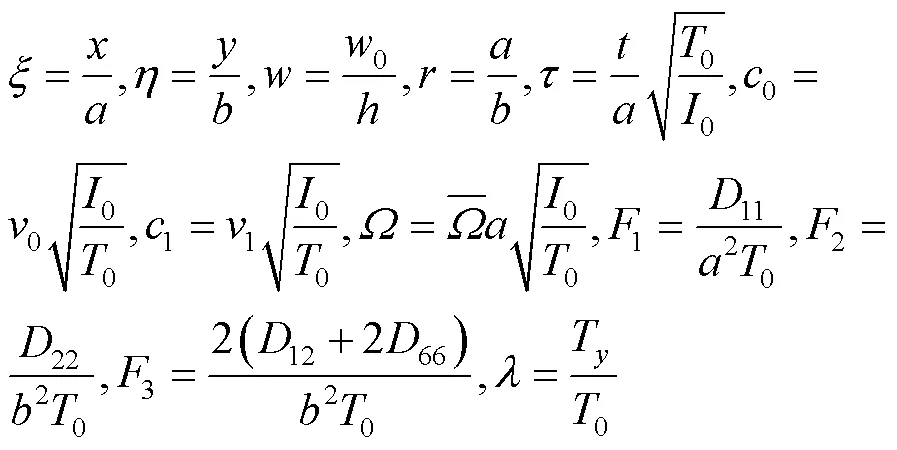
将式（6）代入式（5）得无量纲平衡方程为：

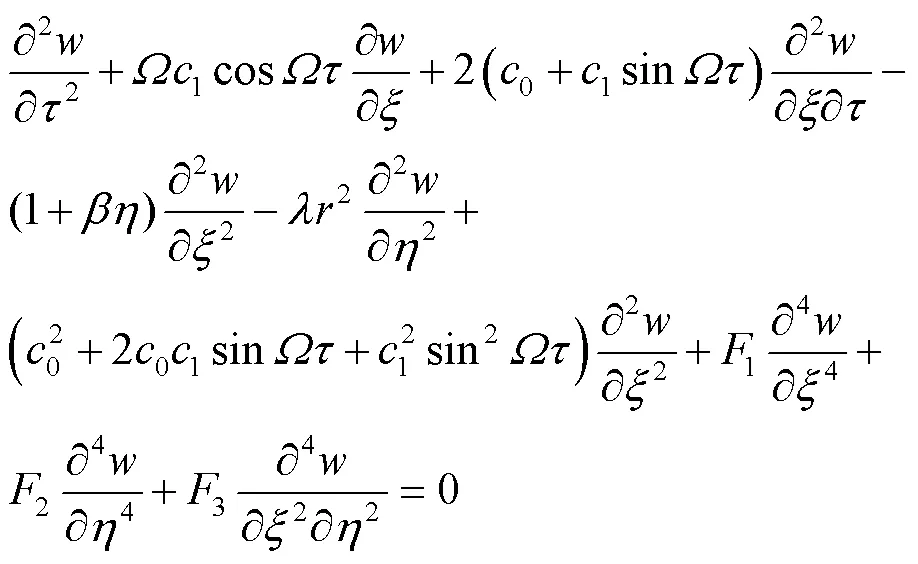
2 应用微分求积法建立复特征方程

多方程的微分求积形式为：

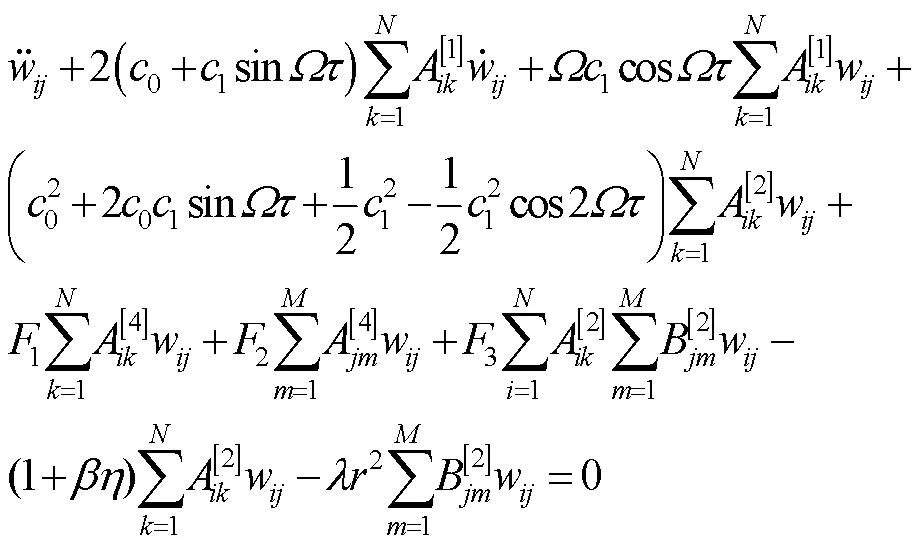
四边简支边界条件的微分求积形式为：

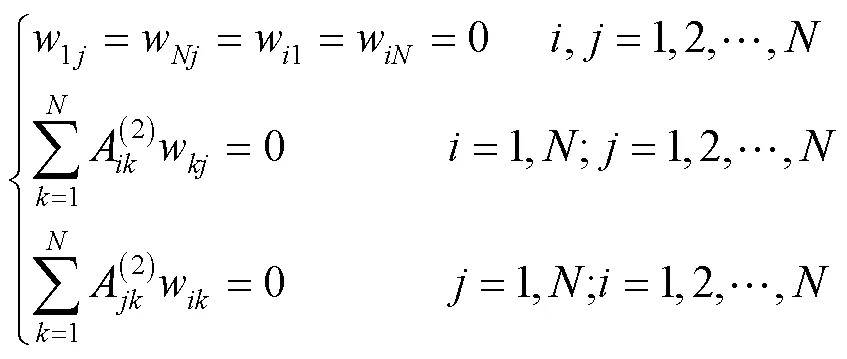
对边简支另一对边固支的微分求积形式为：

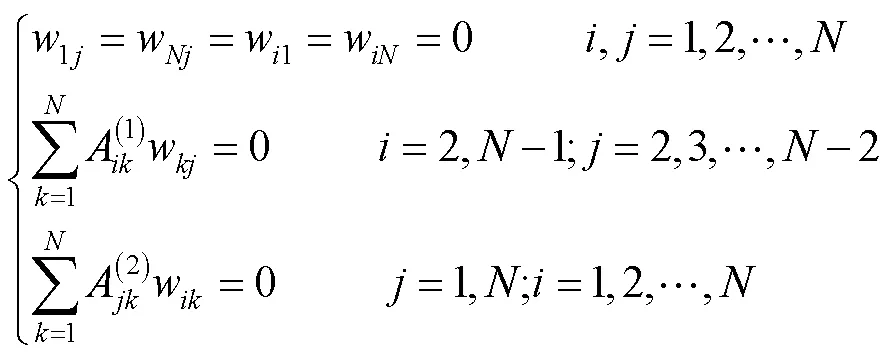
将方程（8）和边界条件（9）、（10）合并得：

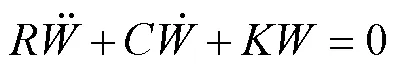
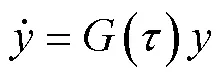
3 微分方程组的求解

应用二阶四级隐式龙格库塔法求解该运动微分方程组。求解公式为：

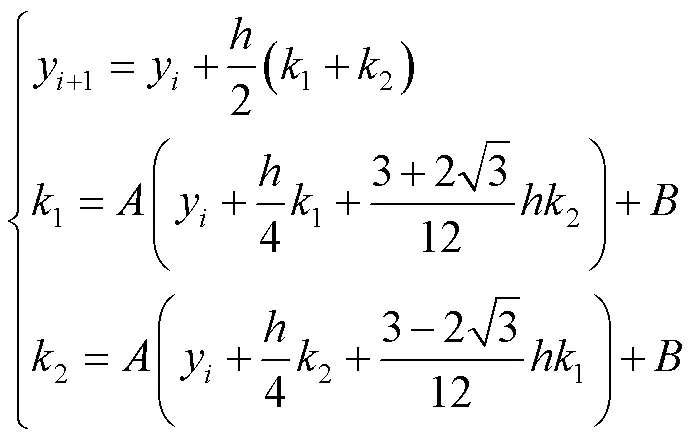
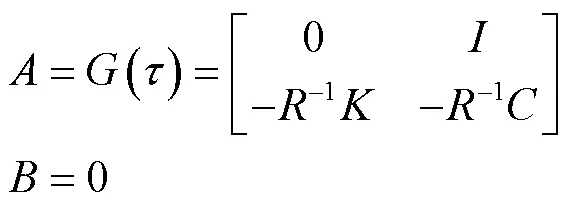
4 数值计算与分析

下面以一种功能薄膜进行数值分析，材料属性见表1。

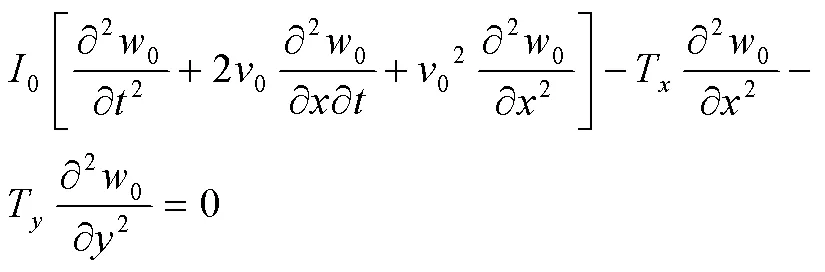
表1 功能膜各层材料属性

Tab.1 Material properties of each layer of functional film

表2 三层铺设四边简支复合膜前3阶固有频率文中解与解析解的对比

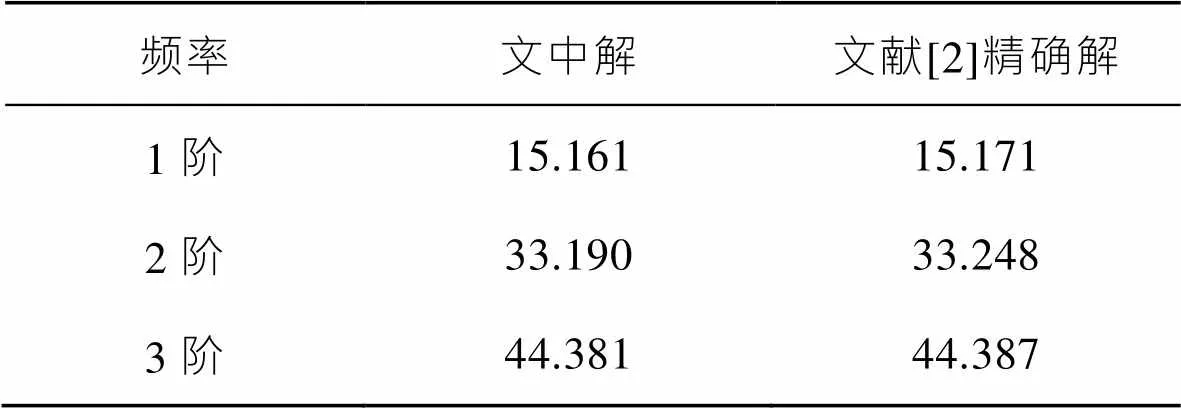
Tab.2 Comparison between the solution and the analytical solution of the first three order natural frequencies of the three-layer simply supported composite film

表3 单层膜前3阶固有频率本文解与解析解的对比

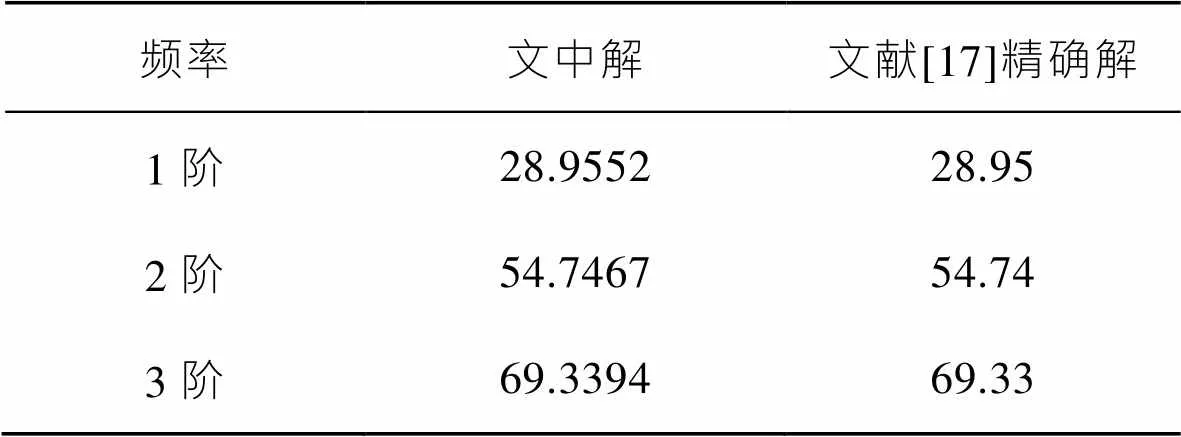
Tab.3 Comparison between the solution and the analytical solution of the first three order natural frequencies of monolayers

方程（16）与文献[12]轴向运动薄膜的横向振动微分方程一致。

由表2、表3和式（16）可知，式（5）计算非均匀张力作用下多层膜结构轴向运动横向振动微分方程正确，并且应用微分求积法计算不同边界条件下多层膜结构的振动频率与文献解析解均有很好的一致性，表明该方法研究多层膜结构动力稳定性是可行的。

4.1 四边简支边界计算分析

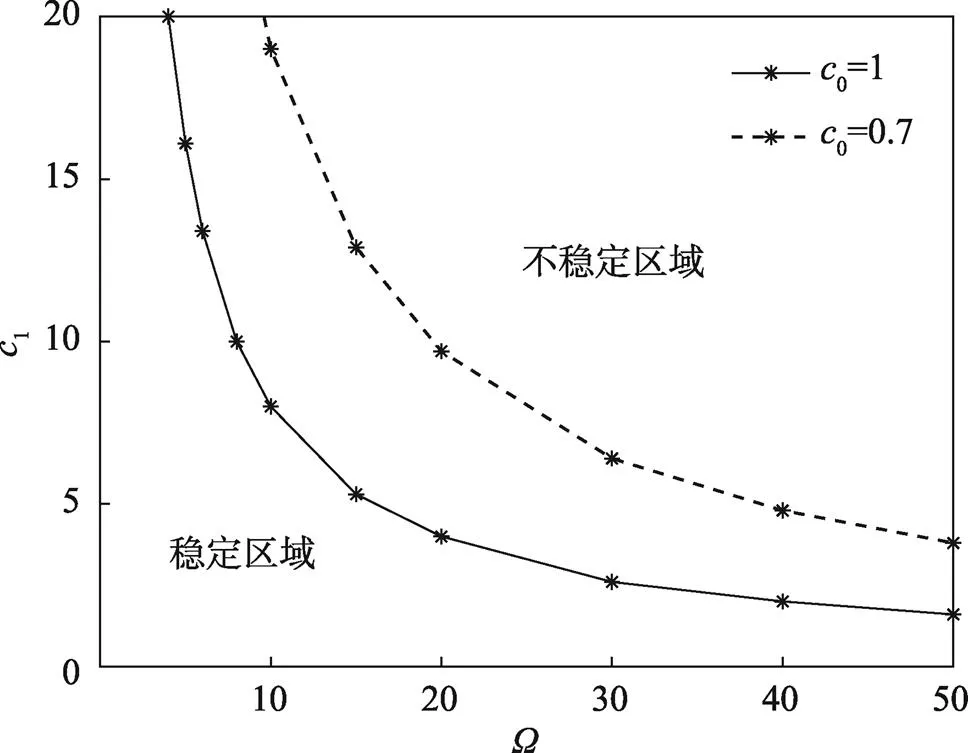
图5 平均速度与稳定区域的关系

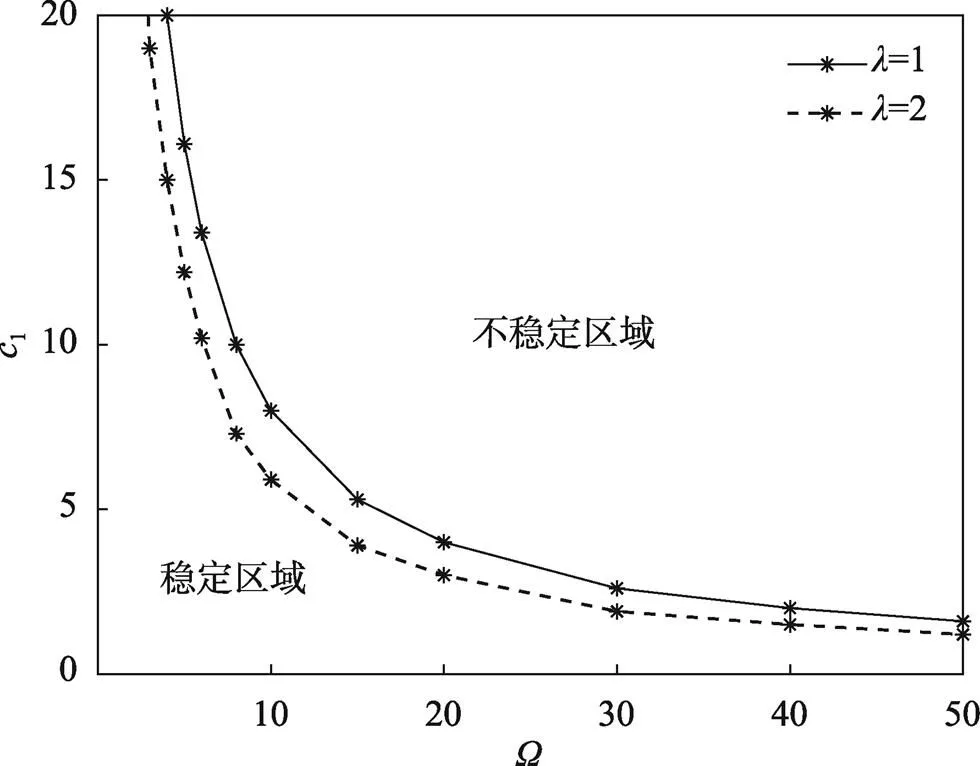
图6 张力比与稳定区域的关系

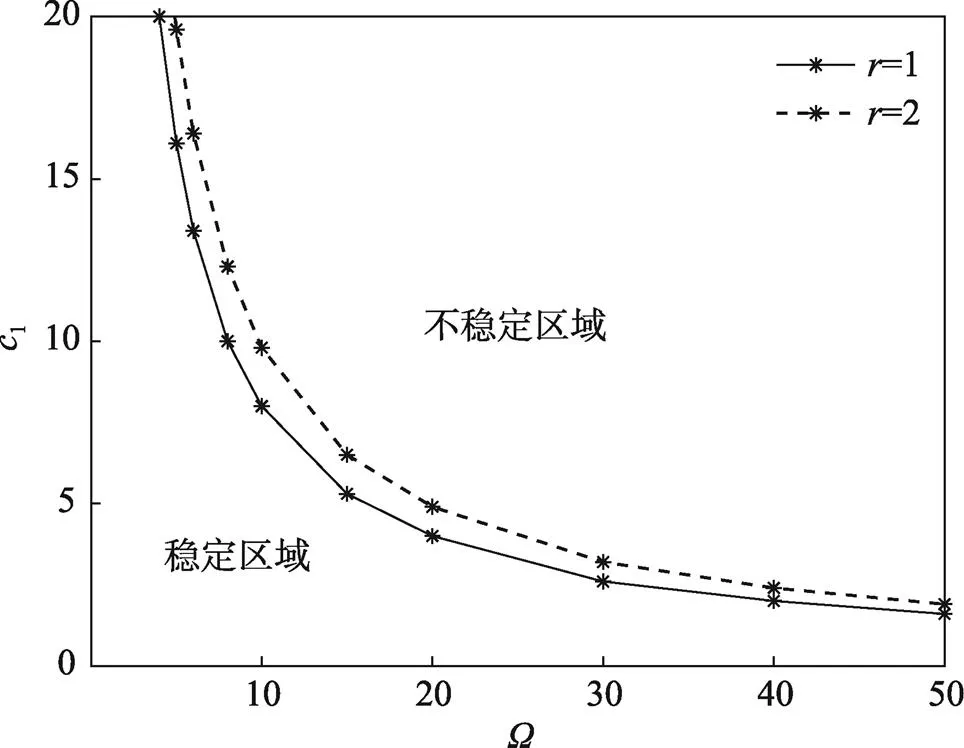
图7 长宽比与稳定区域的关系

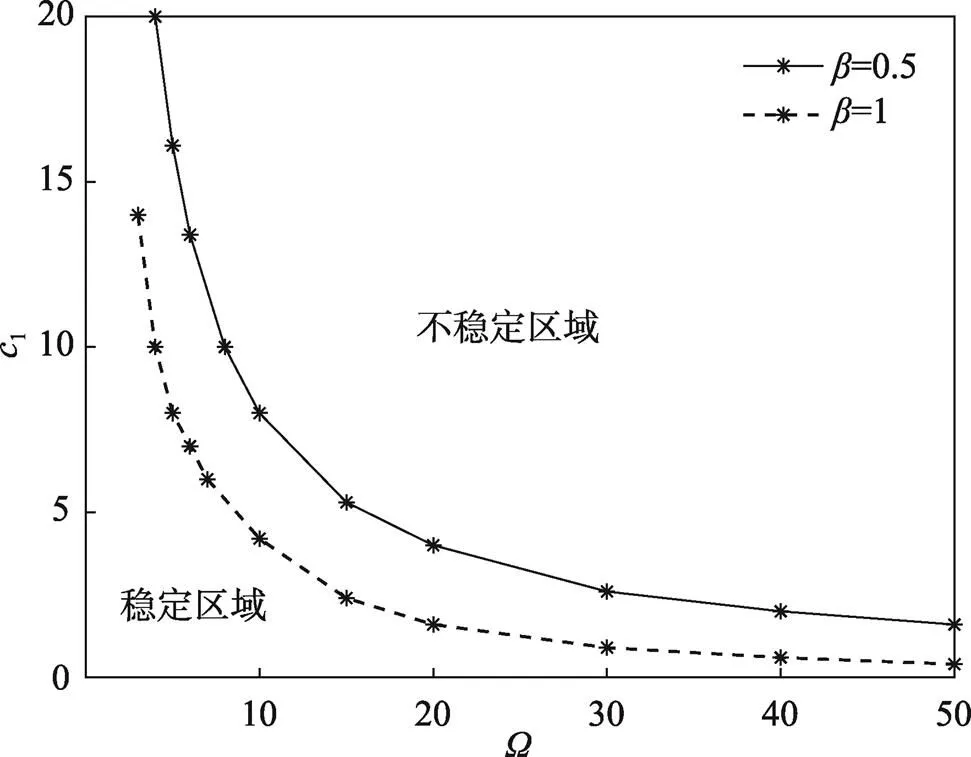
图8 非均匀张力系数与稳定区域的关系

4.2 对边简支对边固支边界计算分析

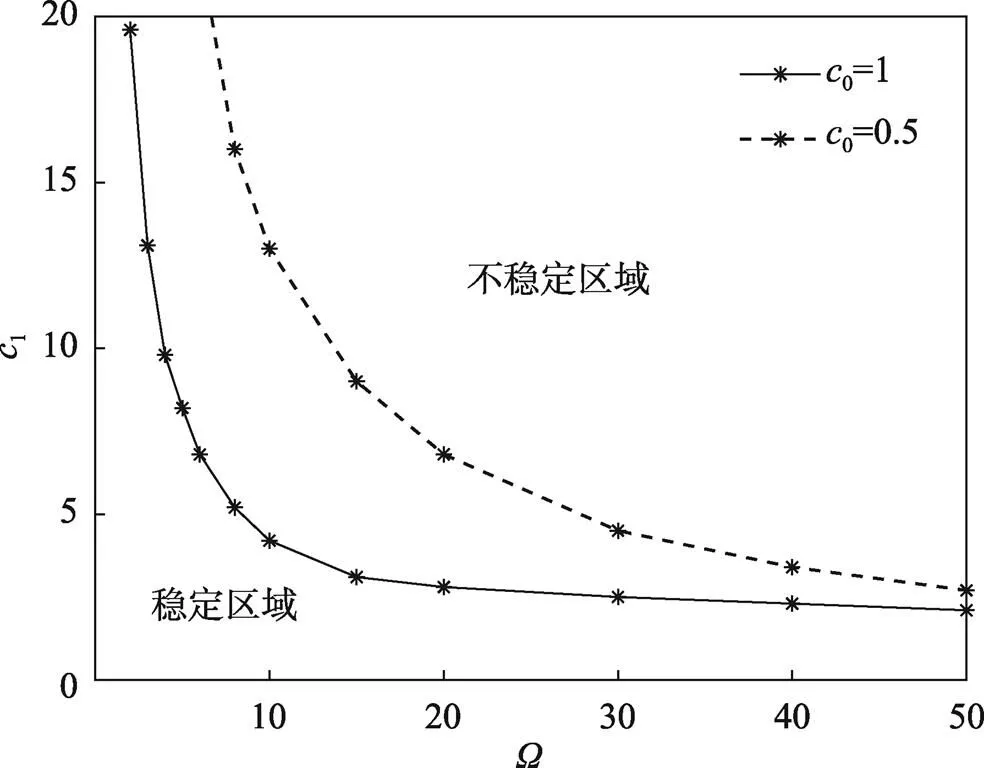
图9 平均速度与稳定区域的关系

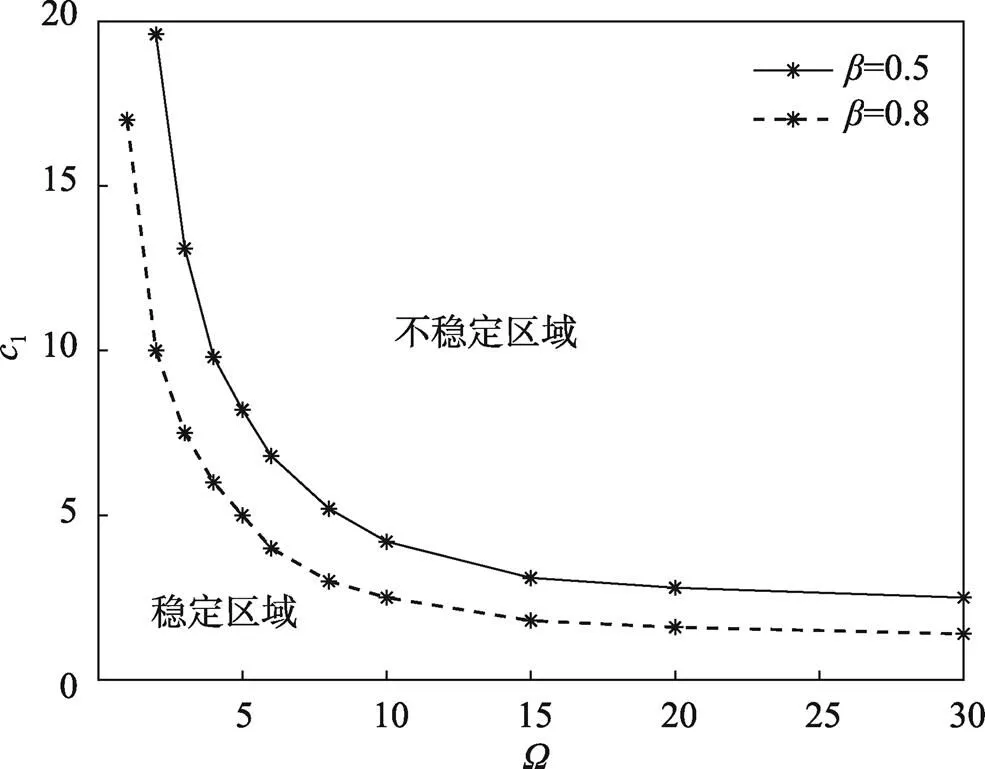
图10 非均匀张力系数与稳定区域的关系

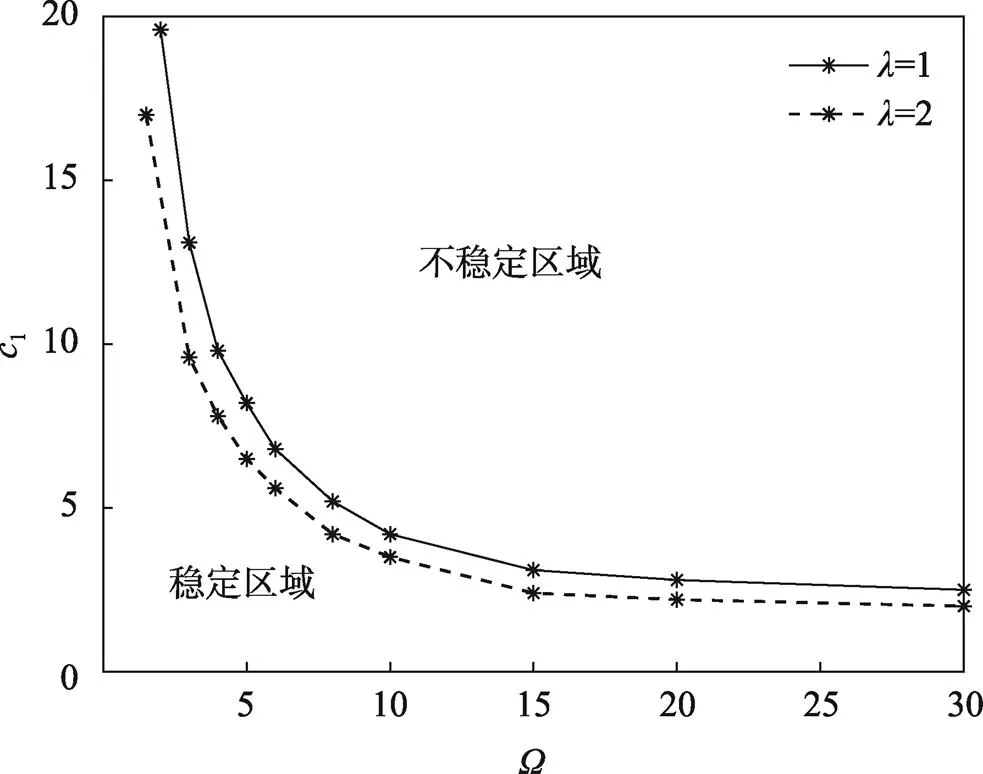
图11 张力比与稳定区域的关系

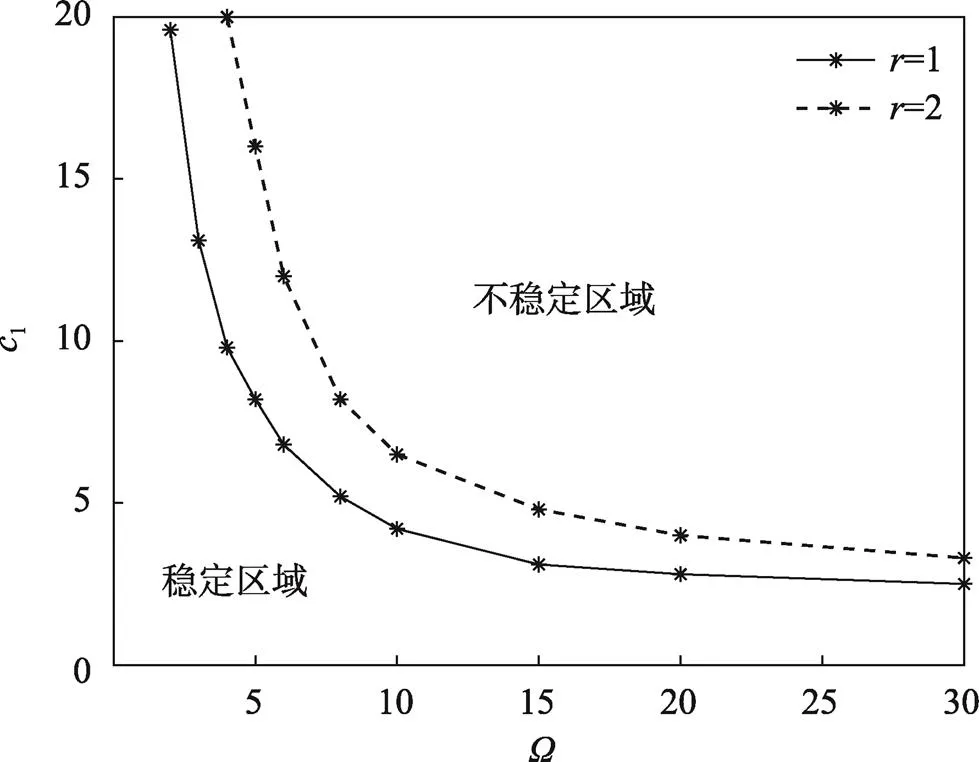
图12 长宽比对稳定区域的影响

5 结语

文中研究了变速度多层膜结构在非均匀张力作用下的稳定性，以正弦速度变化的无量纲频率和幅值为横纵坐标，绘制了动力稳定性方程特征值为1时的稳定区域边界变化曲线，说明了速度以正弦扰动时，速度变化的幅值与频率越小，越有利于系统的平稳运行。同时分析了系统不同参数对运动多层膜结构稳定传输的作用规律，研究结论如下。

1）对于非均匀张力下运动多层膜结构，增大平均速度、张力比、非均匀张力系数，系统的稳定区域会变小；增大长宽比，运动多层膜的稳定区域会变大。

2）在系统不同参数中，平均速度的变化对运动多层膜稳定区域的影响最为显著。

3）当边界条件为对边简支对边固支时，动态稳定曲线在=15之后变的平缓，当边界条件为四边简支时，动态稳定曲线在=50之后才变的平缓。由此可知，四边简支边界对速度变化频率更为敏感，在相同条件下，对边简支对边固支边界比四边简支边界的稳定区域更大。

该研究对提高运动多层薄膜结构印刷质量、改善柔性电子薄膜印刷在变速运动工况下镀层平整性与套印准确性，确保薄膜稳定传输有重要参考意义。

[1] 尹周平, 黄永安. 柔性电子制造材料、器件与工艺[M]. 北京: 科学出版社, 2016: 285-300.

YIN Zhou-ping, HUANG Yong-an. Flexible Electronic Manufacturing Materials, Devices and Technologies[M]. Beijing: Science Press, 2016: 285-300.

[2] 赵飞, 吴锦武, 赵龙胜. 采用分层理论计算层合板的固有频率和振型[J]. 噪声与振动控制, 2014, 34(2): 34-40.

ZHAO Fei, WU Jin-wu, ZHAO Long-sheng. Analysis for Natural Frequencies and Mode Shapes of Laminated Composite Plates Using Layerwise Theory[J]. Noise and Vibration Control, 2014, 34(2): 34-40.

[3] 刘金建, 谢锋, 姚林泉, 等. 基于非局部理论的轴向运动黏弹性纳米板的参数振动及其稳定性[J]. 振动与冲击, 2017, 36(19): 13-20.

LIU Jin-jian, XIE Feng, YAO Lin-quan, et al. Parametric Vibration and Stability of an Axially Moving Viscoelastic Nanoplate Based on the Nonlocal Theory[J]. Journal of Vibration and Shock, 2017, 36(19): 13-20.

[4] 陈立群, 唐有绮. 面内变速运动粘弹性板的非线性参数振动[C]// 第四届全国动力学与控制青年学者研讨会论文摘要集, 大连, 2010: 5-6.

CHEN Li-qun, TANG You-qi. Nonlinear Parametric Vibration of a Viscoelastic Plate Moving At Variable Speed in Plane[C]// Abstracts of The 4th National Symposium on Dynamics and Control for Young Scholars, Dalian, 2010: 5-6.

[5] YANG X, CHEN L, ZU J. Vibrations and Stability of an Axially Moving Rectangular Composite Plate[J].Journal of Applied Mechanics,2011,78(1): 011018.

[6] LU S, XUE N, ZHANG W, et al. Dynamic Stability of Axially Moving Graphene Reinforced Laminated Composite Plate under Constant and Varied Velocities[J]. Thin-Walled Structures, 2021, 167: 108176.

[7] 刘金堂, 杨晓东, 张宇飞, 等. 轴向变速运动正交各向异性板的动态稳定性[J]. 应用力学学报, 2010, 27(1): 49-52.

LIU Jin-tang, YANG Xiao-dong, ZHANG Yu-fei, et al. Dynamic Stability of Axially Accelerating Orthotropic Plates[J]. Chinese Journal of Applied Mechanics, 2010, 27(1): 49-52.

[8] HATAMI S, RONAGH H R, AZHARI M. Exact Free Vibration Analysis of Axially Moving Viscoelastic Plates[J]. Computers and Structures, 2008, 86(17/18): 1738-1746.

[9] AYDOGDU M. A New Shear Deformation Theory for Laminated Composite Plates[J]. Composite Structures, 2009, 89(1): 94-101.

[10] MARYNOWSKI K. Vibration Analysis of an Axially Moving Multiscale Composite Plate Subjected to Thermal Loading[C]// International Conference on Engineering Vibration (ICoEV), 2018.

[11] HAN W, DICKINSON S. Free Vibration of Symmetrically Laminated Skew Plates[J], Journal of sound and vibration, 1997, 208(3): 367-390.

[12] 侯志勇, 王忠民. 轴向运动薄膜的横向振动和稳定性分析[J]. 西安理工大学学报, 2005, 21(4): 402-404.

HOU Zhi-yong, WANG Zhong-min. The Transverse Vibration and Stability Analysis of an Axially Moving Membrane[J]. Journal of Xi'an University of Technology, 2005, 21(4): 402-404.

[13] 武吉梅. 运动纸带动力学及振动控制研究[D]. 西安: 西安理工大学, 2009: 53-63.

WU Ji-mei. Study on the Dynamics and Vibration Control of the Moving Paper Web[D]. Xi'an: Xi'an University of Technology, 2009: 53-63.

[14] 邵明月. 柔性运动薄膜的非线性动力学研究[D]. 西安: 西安理工大学, 2019: 35-46.

SHAO Ming-yue. Nonlinear Dynamics of Flexible Moving Membranes[D]. Xi'an: Xi'an University of Technology, 2019: 35-46.

[15] WU J, QING J, SHAO M, et al. Vibration Characteristics and Stability of a Moving Membrane with Variable Speed Subjected to Follower Force[J]. Journal of Physics: Conference Series, 2020, 1545(1): 012008.

[16] 卢瑶, 武吉梅, 王砚, 等. 随从力作用下变速运动粘弹性硬质薄膜的稳定性研究[C]// 2018年全国固体力学学术会议摘要集, 哈尔滨, 2018: 483.

LU Yao，WU Ji-mei，WANG Yan，et al. Study on The Stability of Viscoelastic Hard Films Moving at Variable Speed Under Follower Force[C]// Abstracts of 2018 National Conference on Solid Mechanics, Haerbin, 2018: 483.

[17] GOMAN D J. Free vibration analysis of rectangular plates[M]. Elsevier North Holland, 1982.

Dynamic Stability of Multilayer Film Structure under Non-uniform Tension

SHAO Ming-yue1, ZHANG Miao1, WU Ji-mei1, QING Jia-juan2, WANG Jing2

(1. School of Printing Packaging Engineering and Digital Media Technology, Xi'an University of Technology, Xi'an 710054, China; 2. School of Mechanical and Precision Instrument Engineering, Xi'an University of Technology, Xi'an 710048, China)

non-uniform tension; variable speed; multilayer film structure; dynamic stability

TB486

A

1001-3563(2022)15-0195-08

10.19554/j.cnki.1001-3563.2022.15.022

2021–12–05

国家自然科学基金（52075435）；陕西省自然科学基金（2021JQ-480）；陕西省教育厅自然科学专项项目（21JK0805）

邵明月（1989—），女，博士，西安理工大学讲师，主要研究方向为机械结构动力学。

责任编辑：曾钰婵