基于机器学习的声表面波温度传感器快速优化设计
2022-08-23杨自由范彦平张晓焱
杨自由,范彦平,张晓焱
工艺与装备
基于机器学习的声表面波温度传感器快速优化设计
杨自由,范彦平,张晓焱
(上海理工大学 光电信息与计算机工程学院 上海 200093)
为提高声表面波谐振器(SAWR)性能,制造高性能声表面波(SAW)温度传感器。通过FEM/BEM理论,建立SAW温度传感器精确仿真优化模型,基于此模型对敏感基片的欧拉角进行大步长优化;同时,结合仿真数据并利用多项式回归模型对敏感基片的欧拉角进行小步长快速优化。文中提出的FEM/BEM仿真模型与机器学习相结合优化设计方法不仅能够实现SAWR的精确模拟,而且可大幅提高优化效率。优化结果与实际器件的中心频率相对误差为0.4%,值相对误差为1.2%。文中提出的FEM/BEM仿真模型与机器学习相结合优化设计方法与纯FEM/BEM方法相比,单个切型计算速度提高了2 000多倍。所设计的优化系统可用于谐振器敏感基片切型的快速优化设计,可缩短高性能SAW温度传感器的开发周期。
声表面波;机器学习;多项式回归;温度传感器
温度监测在物品包装储运过程中起着至关重要的作用,不同物品在包装储运的过程中对温度的需求各不相同,如在(4±1)℃时,猕猴桃的保鲜时间最长,且温度波动幅度越小越有利于延缓猕猴桃的衰老速度[1];在温度为(0.6±0.1)℃的精准温控保温箱内贮藏14 d后的黄花菜,其维生素C、还原糖、黄酮含量显著高于普通保温箱贮藏的黄花菜[2]。小黄鱼在不同的温度下贮藏相同一段时间后,其菌落总数与贮藏温度成正比,持水率与贮藏温度成反比[3]。对物品的包装储运过程的温度进行严格监测具有重要意义。目前常用的测温方法主要使用的测温仪器有DS18B20温度传感器[4]、分布式光纤温度传感器[5]和红外温度传感器[6]等,这些测温仪器用在物品包装储运的过程中,存在布线难、成本高、电池供电需要定期维护、漏电等问题,此外,还存在光纤易折断以及红外线只能测量无遮挡物体的外表温度等问题,因此需要开发一种新的测温方法。
声表面波(SAW)温度传感器具有超小型、高可靠性、高灵敏度、准数字输出易于集成等优点,利用器件本身的高频特性和基片的压电特性可以使传感器进行无源无线测量,并可在各种恶劣的环境下工作。声表面波温度传感器有延迟线型和谐振型2种结构。与延迟线型结构的SAW器件相比,声表面波谐振器(SAWR)具有品质因数高、插入损耗低、稳定性好等特点。国内外很多学者从敏感基片以及电极结构参数等方面对SAWR的品质因数()、频率温度系数(TCF)、机电耦合系数(²)等性能参数进行了优化。吉小军等[7]提出了敏感基片优化选择的基本准则,并以硅酸镓镧为例进行了分析和优化选择。俞宽新等[8]使用循环迭代的方法,以机电耦合系数为准则确定了铌酸锂基底的最佳切割方向。计算一个铌酸锂切型平均耗时高达5 min。Li等[9]利用P矩阵方法,通过改变电极的厚度和IDT数量分别对灵敏度和插入损耗进行了优化,其仿真结果与实际插入损耗的相对误差高达9%,每改变一次电极参数进行仿真计算需花费3 min左右。通过前期的研究对比发现,常规的仿真优化方法存在优化精度低、优化周期长、忽略电极影响等问题。
文中采用边界元法(Boundary Element Method, BEM)对半无限压电基片进行模拟;利用有限元法(Finite Element Method, FEM)对任意形状金属电极的力学效应进行模拟,实现对声表面波器件的精确模拟。针对该模型耗时长的问题,结合机器学习,在采用仿真模型进行大步长欧拉角仿真的基础上,利用多项式回归模型对SAWR的不同欧拉角进行更精确的预测,以加快优化流程。
1 SAW温度传感器的仿真
1.1 仿真模型建立与验证
文中使用FEM/BEM对有限长SAW温度传感器进行模拟仿真。在FEM/BEM中,敏感基片上所有的声学效应、电学效应,以及电极的质量加载效应都被考虑在内,FEM对电极的质量加载效应进行模拟仿真,BEM对敏感基片上的SAW传播进行模拟仿真。使用FEM/BEM可以准确地对任意切型、任意电极结构参数的SAW温度传感器进行精确模拟仿真。
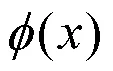
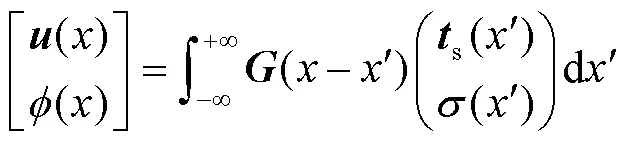
式中:G(x)为空间域广义格林函数,可由慢度域广义格林函数通过傅里叶变换得到。详细变化过程可参考文献[10]。
第根电极的应力和电荷分布的切比雪夫多项展开式为:

式中:chi为多项式加权的最大阶次,a、c分别为第根电极宽度的一半和电极的中心位置。结合式(2)与BEM,可得到线性方程组:


图2 42°Y–LiTaO3的导纳曲线
从图2可以看出,文中的计算结果与参考文献结果非常接近,仿真结果与实际器件的中心频率相对误差为0.4%,值相对误差为1.2%,微小的差异可能是计算过程中采用的材料参数不同导致的。
1.2 SAWR大步长仿真优化
SAWR的性能的好坏直接决定SAW温度传感器的好坏,设计SAW温度传感器的本质是设计高性能SAWR。文中选用石英晶体作为压电基片,由于石英晶体的各向异性,声表面波温度传感器的性能在晶体的不同切割与传播方向上有很大差异,要充分用压电晶体的优良特性,使相应的传感器达到最佳性能,就需要对石英基片的切割与传播方向进行优化选择。欧拉角(,,)用来表示基片的切割与SAW的传播方向,根据三角晶系32点群结构的对称性[13],切向优化可在3个欧拉角(为0~120°、为0~180°、为0~90°)的角度范围内进行优化计算,其他欧拉角的计算参数可通过三角晶系的对称性得到。为了找出高性能的SAW温度传感器的压电晶体切型,需要对所有的欧拉角进行系统计算,这需要很大的计算量。为了优化数值计算的过程,采用FEM/BEM模型对SAWR进行大步长优化。以值为优化指标,设置角度变化步长为10°,角度变化步长为15°,角度变化步长为10°。使用FEM/BEM模型进行仿真,仿真的部分结果见表1。
表1 FEM/BEM仿真结果部分数据集
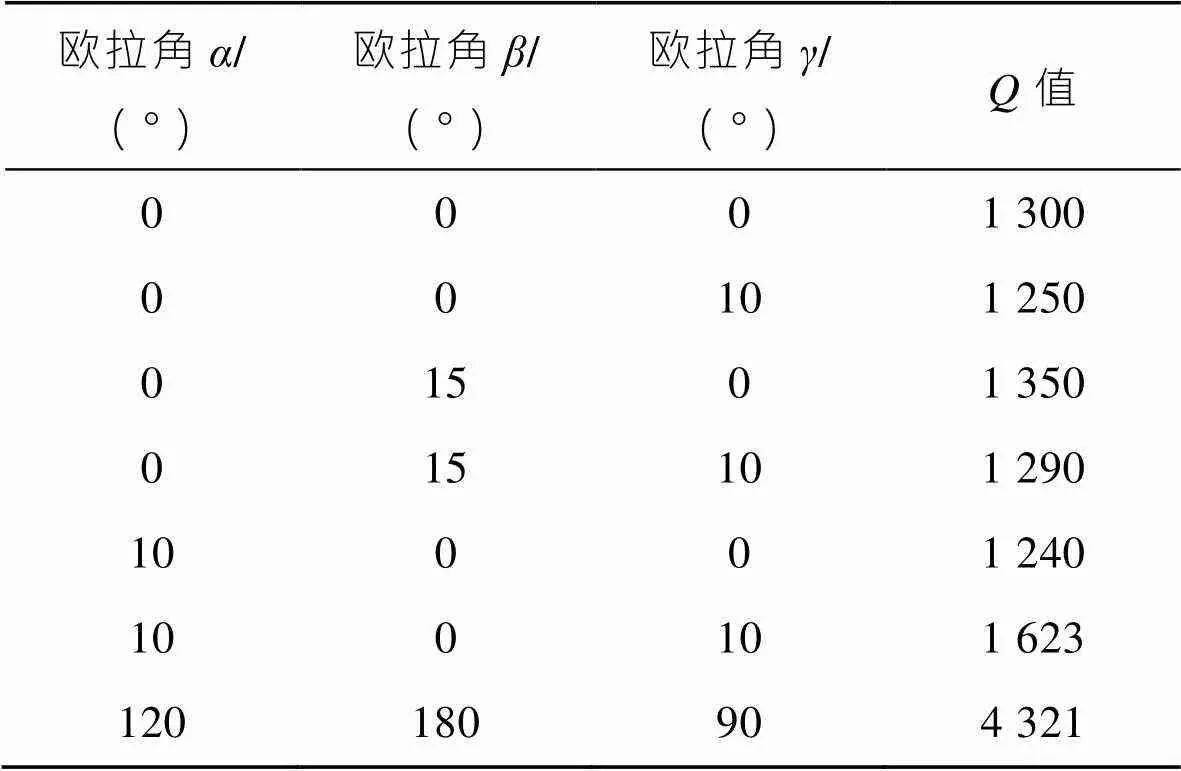
Tab.1 Partial data set of FEM/BEM simulation results
观察表1可知,不同的欧拉角,其值差异很大。为更好地观察在欧拉角改变时,值的变化情况,和放置为0°,此时SAWR的值随角的变化见图3。
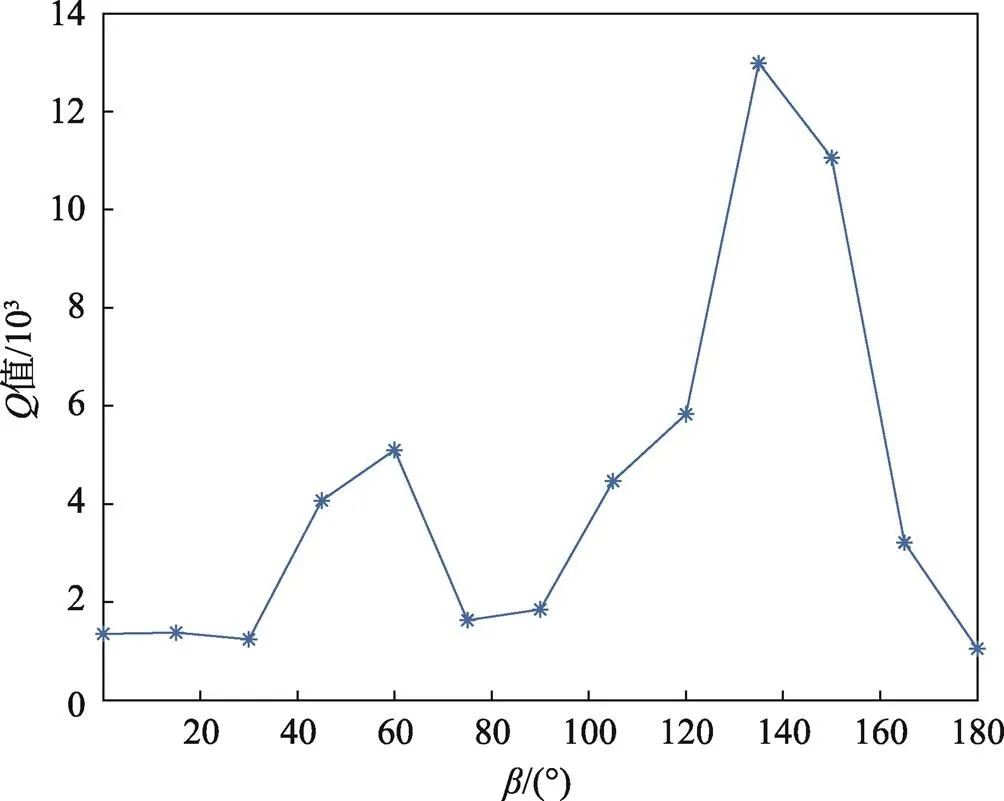
图3 Q值仿真结果
由图3可知,不同角度的欧拉角,其SAWR的值差异很大。虽然优化过程中利用晶体的对称性以及大步长的方法,对优化过程的时间有了大幅提高,但是每个切型的仿真计算平均需要花费10 min[14],如果再进行小步长优化将会花费更长的时间,效率较低。
2 多项式回归模型
虽然FEM/BEM模型能精确模拟压电基片内的各场量,但计算量太大,计算花费时间过长,因此,文中利用FEM/BEM对敏感基片的欧拉角进行大步长仿真,结合机器学习模型,对压电基片进行欧拉角小步长优化。使用机器学习模型[15-17]对敏感基片的优化流程见图4。
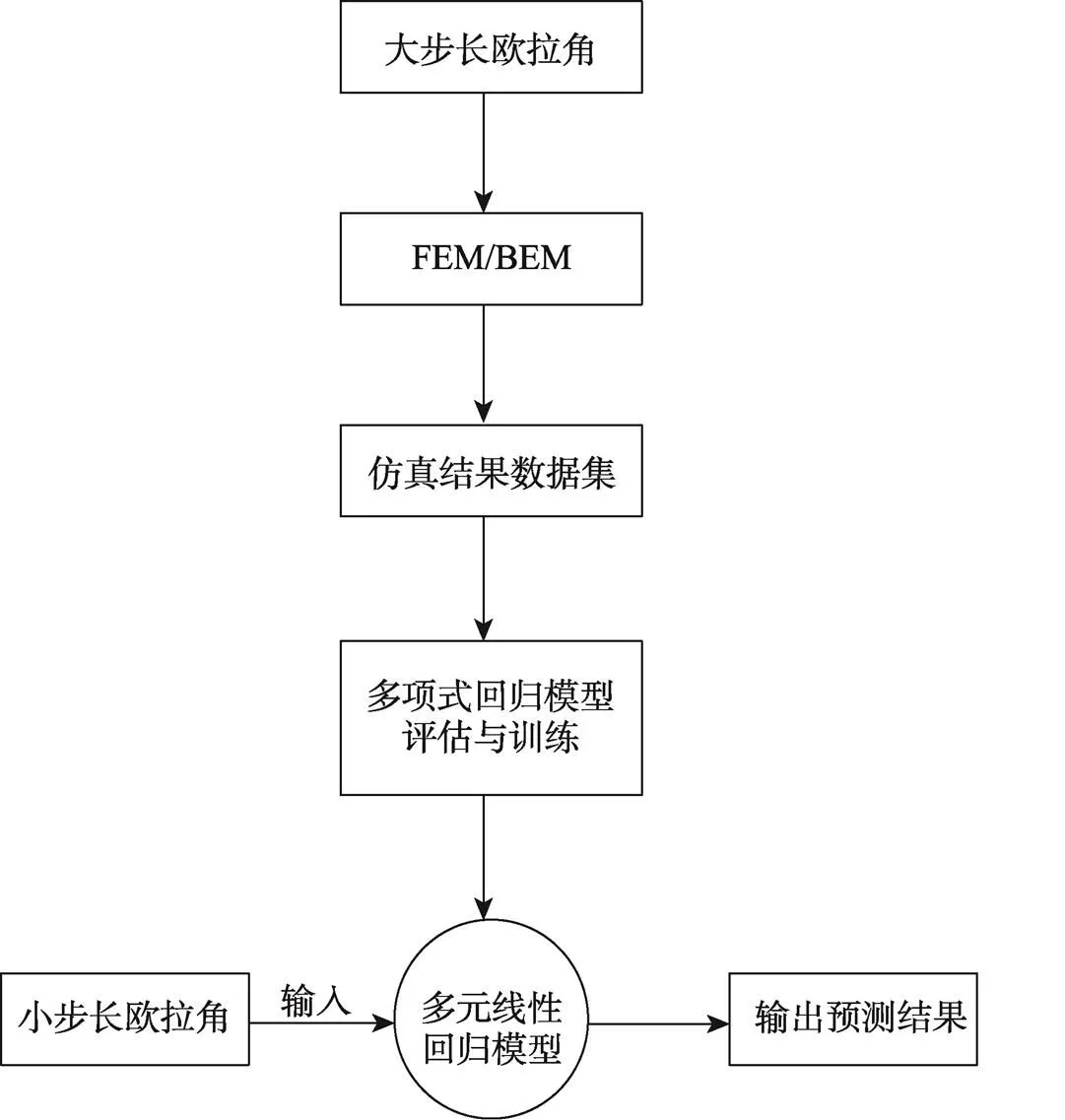
图4 SAW温度传感器快速优化流程
首先对欧拉角设置大步长,使用FEM/BEM模型进行仿真,这个方法精度高,但速度慢。在FEM/BEM结果的基础上,对步长之间的结果用多项式回归模型来预测,这时候大步长之间的参数变换可近似线性表示。设置多项式回归模型的单次输入自变量为欧拉角、、,接着对欧拉角每次变化的幅度减小,使用多项式回归模型进行值的预测。由于FEM/BEM优化效率低,所以对欧拉角每次变化的幅度设置较大,这样既提高了优化效率,也尽可能地遍历所有的欧拉角,提高了多项式回归模型训练数据的准确性。多项式回归对欧拉角的优化效率很高,因此每次变化的幅度设置较小,并遍历所有的欧拉角,不仅提高了优化效率也提高了优化精度。
文中实验设备的CPU为Intel i7–8700K,GPU为AMD WX 2100,运行内存为64 G。在Python3.8的编程环境下通过调用Scikit–learn库中的内置函数PolynomialFeatures、LinearRegression、MakePipeline完成此次实验。
2.1 多项式回归模型的建立
SAW传感器值的影响因素众多,但文中只研究压电基片的欧拉角对值的影响。结合FEM/BEM仿真数据集,构造关于欧拉角(、、)的多项式回归模型[18]如下:
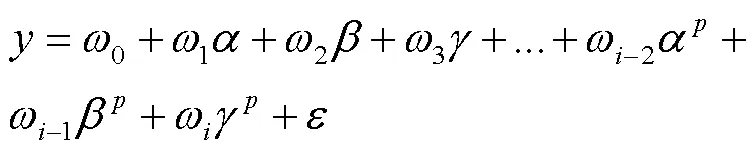
式中:因变量为SAW传感器的品质因数;0、1、2、…、ω为回归系数;为随机偏差;为多项式的阶数,文中取6。令=1、=2、=3、…、γ=x,进行变量替换得到多元线性回归模型:
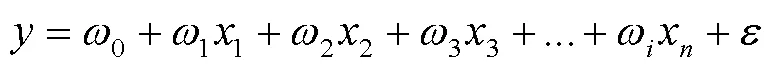
式中:0、1、2、…、ω为回归系数。使用PolynomialFeatures生成特征数据集,再放入LinearRegression中进行预测。同时使用MakePipeline将两者封装起来,建立完整的值预测模型。
2.2 多项式回归模型预测能力的评估
为了评估模型的预测能力,文中采用均方误差(RMSE)、平方绝对误差(MAE)和决定系数2这3个误差度量指标来衡量模型预测值与实际值之间的关系。在这些误差度量指标中,预测模型的准确率用决定系数2来衡量,而算法的误差则采用MAE值和RMSE值进行衡量,MAE值和RMSE值的取值范围为[0,∞],数值越小说明预测模型算法的可靠性越高。决定系数2的数值越接近于1,说明估计模型的可靠性越高。
采用Python语言进行预测模型的搭建,同时为了防止过拟合现象产生并且提高模型的泛化能力,将多项式回归模型进行–折交叉验证[19-20],其中取4。将敏感基片的仿真数据分为4组互斥子集,每次抽取出4份中的1份作为测试集,剩下的3份作为训练集。依次计算得到决定系数、均方误差和平均绝对误差4次的迭代结果,然后求出4次迭代的平均值,用求得的平均值评估多项式回归模型的总体效果。多项式回归模型的4次计算结果见表2。
表2 多项式回归模型的误差度量
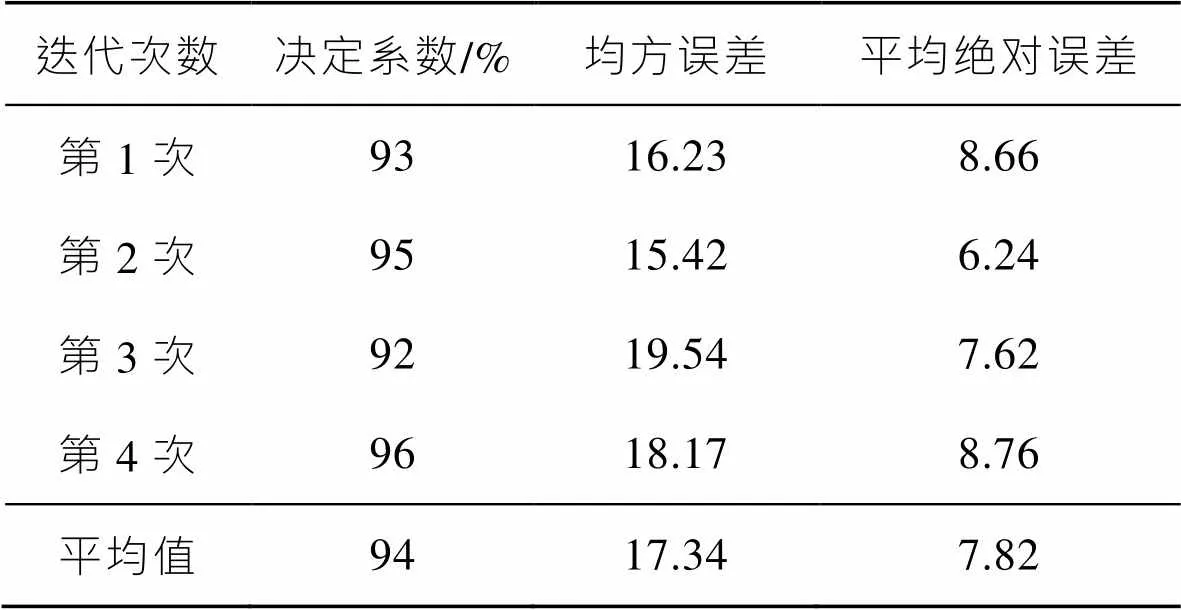
Tab.2 Error Measures of Polynomial Regression Model
由表2可以看出,值的平均决定系数2为94%、均方根误差为17.34、平均绝对误差为7.82,多项式回归模型对文中数据的预测总体效果很好,说明多项式回归模型可用于对声表面波温度传感器的快速优化研究。
3 基于多项式回归模型的SAW温度传感器快速优化
为解决FEM/BEM优化时存在的占时过长的问题,使用多项式回归模型对SAW温度传感器进行快速优化。以Python语言为工具,以FEM/BEM得到的仿真数据为训练集,训练集具体构成见表1,对多项式回归模型进行训练。设置欧拉角(、、)的步长均为1,将其作为自变量输入经过训练的多项式回归模型中,对值进行预测。为更好地观察多项式回归模型的预测结果与仿真结果之间的误差,单独将和角设为0°,角的步长设为3°进行了仿真计算。在和为0°,仿真步长为3°,多项式回归预测步长为1°时,声表面波谐振器的值变化情况见图5。

图5 Q值的预测结果
由图5可知,SAW温度传感器的不同压电基片的欧拉角的值差异明显,对欧拉角进行小步长的优化是很有必要的。多项式回归模型的预测结果与FEM/BEM仿真结果基本一致,因此可以用多项式回归模型对SAW传感器进行小步长优化。此外,使用多项式回归模型对声表面波谐振器的欧拉角进行小步长优化,与纯FEM/BEM仿真相比优化速度也得到了大幅提升,单个欧拉角的计算仅需0.2 s,单个切型计算速度提高了2 000多倍。
4 结语
文中以SAW温度传感器为研究对象,建立了FEM/BEM仿真模型,并将仿真结果与实际结果进行了对比。为防止过拟合现象的产生,采用–折交叉验证法对多项式回归模型进行调优,并计算得到值的平均决定系数2为94%、均方根误差为17.34、平均绝对误差为7.82。结合FEM/BEM方法与多项式回归模型设计了SAW温度传感器快速优化方法,并使用该快速优化方法对值进行了预测。文中只选用了多项式回归模型进行预测,后续研究可尝试引入神经网络等方法,使预测结果更接近真实情况。
[1] 熊金梁, 陈爱强, 刘婧, 等. 温度波动对猕猴桃在4℃下货架贮藏品质的影响[J]. 包装工程, 2021, 42(19): 69-76.
XIONG Jin-liang, CHEN Ai-qiang, LIU Jing, et al. Effect of Temperature Fluctuation on the Quality of Kiwifruit during 4 ℃ Shelf Storage[J]. Packaging Engineering, 2021, 42(19): 69-76.
[2] 薛友林, 刘英杰, 张鹏, 等. 精准温控保鲜箱对黄花菜冷藏品质的影响[J]. 包装工程, 2021, 42(15): 1-9.
XUE You-lin, LIU Ying-jie, ZHANG Peng, et al. Effect of Precision Temperature Control Box on Quality of Daylily during Cold Storage[J]. Packaging Engineering, 2021, 42(15): 1-9.
[3] 吴行印, 谢晶, 王旭. 不同贮藏温度下小黄鱼货架期预测模型的建立和评价[J]. 包装工程, 2016, 37(19): 84-90.
WU Xing-yin, XIE Jing, WANG Xu. Establishment and Evaluation of the Shelf-Life Prediction Model for Small Yellow Croaker under Different Store Temperatures[J]. Packaging Engineering, 2016, 37(19): 84-90.
[4] 徐雷, 崔子晨, 刘俊俊, 等. 基于DS18B20温度监测报警系统的设计与实现[J]. 安庆师范大学学报(自然科学版), 2020, 26(1): 89-92.
XU Lei, CUI Zi-chen, LIU Jun-jun, et al. Design and Implementation of Monitoring Alarm System of Temperature Based on DS18B20[J]. Journal of Anqing Normal University (Natural Science Edition), 2020, 26(1): 89-92.
[5] 匡绍龙, 朱学斌. 分布式光纤温度传感器原理及其在变电站温度监测中的应用[J]. 电力自动化设备, 2004, 24(9): 79-81.
KUANG Shao-long, ZHU Xue-bin. Principle of Distributed Optical Fiber Temperature Sensor and Its Application in Substation Temperature Monitoring[J]. Electric Power Automation Equipment, 2004, 24(9): 79-81.
[6] 贝伟仰, 江虹. 基于红外测温的无线温度监测系统的研究[J]. 计算机测量与控制, 2011, 19(10): 2397-2400.
BEI Wei-yang, JIANG Hong. Study of Temperature Wireless Monitoring System Based on Infrared Technology[J]. Computer Measurement & Control, 2011, 19(10): 2397-2400.
[7] 吉小军, 范彦平, 等. 声表面波压力传感器敏感基片优化选择准则研究[C]// 2013中国西部声学学术交流会论文集, 敦煌, 2013: 6-15.
JI Xiao-jun, FAN Yan-ping, et al. Research on Optimal Selection Criteria for Sensitive Substrates of Surface Acoustic Wave Pressure Sensors[C]// Proceedings of 2013 Western China Acoustics Academic Exchange Conference, Dunhuang, 2013: 6-15.
[8] 俞宽新, 刘韬, 王勇. 铌酸锂表面波器件基底最佳切割方向[J]. 北京工业大学学报, 2011, 37(8): 1221-1225.
YU Kuan-xin, LIU Tao, WANG Yong. Optimum Cut Direction of Lithium Niobate as Substrate in Surface Acoustic Wave Devices[J]. Journal of Beijing University of Technology, 2011, 37(8): 1221-1225.
[9] LI Kun, DU Xiao song, HU Jia, et al. Optimization of the Saw Gas Sensor with Two-Port Resonantor[J]. 2009 International Conference on Apperceiving Computing and Intelligence Analysis, ICACIA 2009, 2009: 175-178.
[10] QIAO D, LIU W, SMITH P M. General Green's Functions for SAW Device Analysis[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1999, 46(5): 1242-1253.
[11] RF M, NHC R, REDWOOD M. Analysis of Generation and Detection of Surface and Bulk Acoustic Waves by Interdigital Transducers[J]. IEEE Transactions on Sonics and Ultrasonics, 1977, 24(3): 147-166.
[12] WANG W, ZHANG X, SHUI Y, et al. Minimizing the Bulk Scattering Loss in CRF (DMS) Devices[J]. IEEE Ultrasonics Symposium, 2004, 25(2): 1363-1366.
[13] TARANCHUK A, PIDCHENKO S. Quartz Pulse Wave Sensor with a Capacitive Control for Healthcare Solutions[J]. IEEE Sensors Journal, 2021, 21(6): 8613-8620.
[14] 王为标. 有限长声表面波器件的精确模拟[D]. 南京: 南京大学, 2004: 107-109.
WANG Wei-biao. Accurate Simulation of Finite Surface Acoustic Wave Devices[D]. Nanjing: Nanjing University, 2004: 107-109.
[15] SELVI M V, MISHRA S. Investigation of Performance of Electric Load Power Forecasting in Multiple Time Horizons with New Architecture Realized in Multivariate Linear Regression & Feed-Forward Neural Network Techniques[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 5603-5612.
[16] KUSHAL C, NIRUPAM G, NIKHIL C. Robustness of Iteratively Pre-Conditioned Gradient-Descent Method: The Case of Distributed Linear Regression Problem[J]. Ieee Control Systems Letters, 2021, 5(6): 2180-2185.
[17] MEULENBROEK N E, PICHARDO S. Multiple Linear Regression Estimation of Onset Time Delay for Experimental Transcranial Narrowband Ultrasound Signals[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2021, 68(4): 1032-1039.
[18] 付凌晖, 王惠文. 多项式回归的建模方法比较研究[J]. 数理统计与管理, 2004, 23(1): 48-52.
FU Ling-hui, WANG Hui-wen. A Comparative Reseach of Polynomial Regression Modelling Methods[J]. Application of Statistics and Management, 2004, 23(1): 48-52.
[19] SAEID G, ALIZADEH N A, ALIREZA A S. Robust Particle Swarm Optimization of RFMS for High-Resolution Satellite Images Based on K-Fold Cross-Validation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(8): 2594-2599.
[20] TSUNG W T, YANG Y P. Reliable Accuracy Estimates from K-Fold Cross Validation[J]. IEEE Transactions on Knowledge and Data Engineering, 2019, 32(8): 1586-1594.
Rapid Optimization Design of Surface Acoustic Wave Temperature Sensor Based on Machine Learning
YANG Zi-you, FAN Yan-ping, ZHANG Xiao-yan
(School of Optical-electrical and Computer Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China)
The work aims to improve the performance of surface acoustic wave resonator (SAWR), and manufacture a high-performance surface acoustic wave temperature sensor. Based on the FEM/BEM theory, an accurate simulation optimization model of SAW temperature sensor was established, and the Euler angle of the sensitive substrate was optimized in large steps based on this model. At the same time, the Euler angle of the sensitive substrate was optimized quickly in small steps with the polynomial regression model in combination with the simulation data. The optimization design method combining FEM/BEM simulation model and machine learning proposed in this paper could not only realize the accurate simulation of SAWR, but also greatly improved the optimization efficiency. The relative error of the optimized result and the actual device's center frequency was 0.4%, and the relative error of the Q value was 1.2%. Compared with the pure FEM/BEM method, its speed of single cutting calculation was increased by more than 2000 times. The designed optimization system can be used to quickly optimize the design of the resonator's sensitive substrate cutting, which can shorten the development cycle of high-performance SAW temperature sensors.
surface acoustic wave; machine learning; polynomial regression; temperature sensor
TB486
A
1001-3563(2022)15-0241-06
10.19554/j.cnki.1001-3563.2022.15.028
2021–12–20
国家自然科学基金(51705326,52075339)
杨自由(1995—),男,上海理工大学硕士生,主攻方向为声表面波传感器优化设计。
范彦平(1983—),男,博士,上海理工大学副教授,主要研究声表面波传感器设计及信号处理。
责任编辑:曾钰婵
