基于超强耦合腔光力系统制备的宏观量子态特性分析
2022-08-22王晶晶刘玉洁郑丽
王晶晶,刘玉洁,郑丽∗
(1大连工业大学光子学研究所,辽宁 大连 116034;2大连工业大学基础教学部,辽宁 大连 116034)
0 引言
宏观系统中量子行为的存在性问题一直吸引着众多的物理学家。一方面,从认识物理世界的角度,宏观系统的量子效应与量子力学和广义相对论背后潜在的新物理有密切的联系。另一方面,量子科学与量子技术的发展趋势表明,未来的量子系统将会向更复杂、更宏观的方向发展,新的技术革新必将由此产生。因此,认识宏观物体的量子性存在的机制或宏观量子性存在的机制,并在此基础上探索如何有效地消除环境对宏观量子性的影响,以及如何控制宏观量子态,是十分有意义的研究。
随着纳米技术和半导体工艺的迅猛发展,人们越来越关注光力学这个新领域,实验中已经可实现的腔光力系统有法布里-珀罗腔、回音壁腔、振动薄膜腔、超导微波腔、光子晶体腔等[1]。目前人们可以利用腔光力系统来制备力学和光学非经典态等[2−4],同时研究量子理论基本问题,如量子退相干、宏观量子叠加以及经典量子边界等[5−8]。
对于单个二能级系统和单模光场耦合的腔量子电动力学系统,人们可以根据原子-腔场的耦合强度与腔场频率的比值,将相互作用情况划分为弱、强、超强、深度强耦合区间[9]。若二能级系统与单模光场的耦合强度Ω小于他们各自的耗散率,则相互作用为弱耦合,如J-C模型;当Ω大于他们各自的耗散率时,相互作用为强耦合[10];最近研究人员在实验中实现了超强耦合相互作用[11−13],此时Ω与腔场共振频率ωC和二能级系统跃迁频率ω的比值满足0.1<Ω/{ω,ωC}<1,能够观察到高阶过程(具有不同激发数的混合状态),之后,Ω/{ω,ωC}=0.1成为超强耦合区间的一个阈值。随着耦合强度进一步增大,达到Ω/{ω,ωC}>1,耦合系统进入深度强耦合区间。2017年,Yoshihara等[14]在电路中通过约瑟夫森结耦合磁通量子比特和LC振荡器,首次在实验上实现了深度强耦合。
文献[8]给出了原子与单模腔场超强耦合作用情况下低能级子空间的有效哈密顿量,文献[15]利用该模型讨论了腔光力系统中制备力学振子的宏观量子叠加态的理论方案,但是没有针对影响宏观量子态量子特性的因素给出更多的分析和讨论。本文主要讨论在超强耦合腔光力系统中,不同的系统初始态对力学振子宏观量子叠加态量子特性的影响,并给出了原子-腔初始状态的最佳参数值。
1 模型
考虑一个由二能级原子、单模法布里-珀罗腔和力学振子组成的系统,法布里-珀罗腔包含一个固定反射镜和一个可移动反射镜,可移动反射镜与机械振子之间通过光机耦合相互关联,则系统哈密顿量为[8]
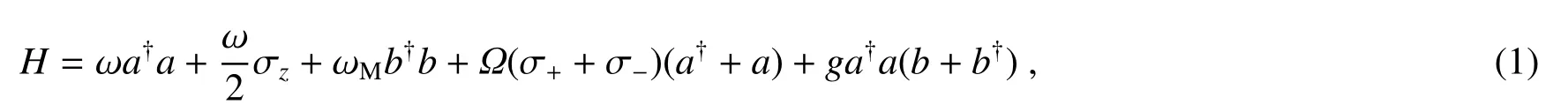
式中:a†和a分别是光场的产生和湮灭算符,σz、σ+、σ−是原子算符,b†和b分别是力学振子的产生和湮灭算符,Ω是二能级原子和腔场的耦合强度,ω是二能级原子的跃迁频率,假设光腔与原子共振,力学振子的固有频率为ωM,腔与力学振子的耦合系数为g。
若考虑原子与腔相互作用超强耦合的情况,即η=Ω/ω≥0.1,低能级子空间中的有效哈密顿量(二阶近似)可表示为[8]
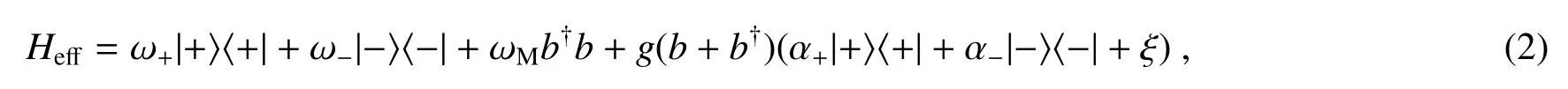
若对光力耦合系数进行调控,使光力耦合近共振且以余弦规律变化,即g→gcos(vt),且v=ωM−δ,v为调控频率,δ为调控引起的失谐量,则该系统的有效哈密顿量变为[15]
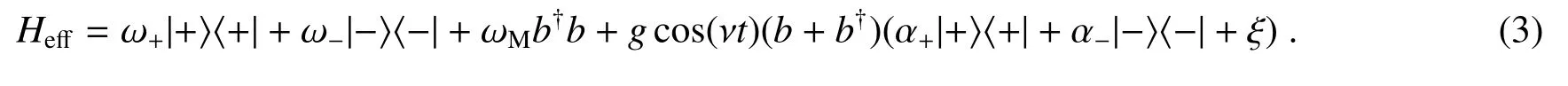
2 相互作用表象的演化算符
利用幺正变换算符

可得相互作用表象中系统的哈密顿量为(旋转波近似)
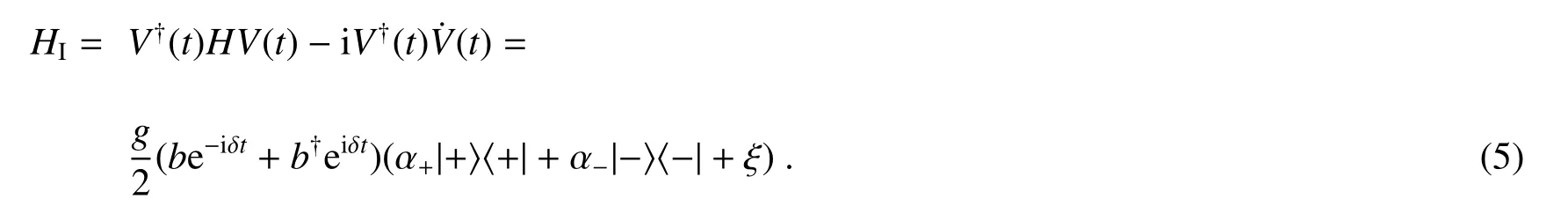
相应于该相互作用表象中的哈密顿量,利用Wei-Norman方法,得到演化算符

3 任意初始态的演化波函数
设t=0时刻,系统的初态为|+0〉=|+〉⊗|0〉m,即原子-腔子系统的初态为|+〉,力学振子的初态为真空态|0〉m。由方程(6),可计算任意t时刻系统的演化波函数为

同理,当系统初态为|−0〉时,任意t时刻系统的演化波函数为


式中
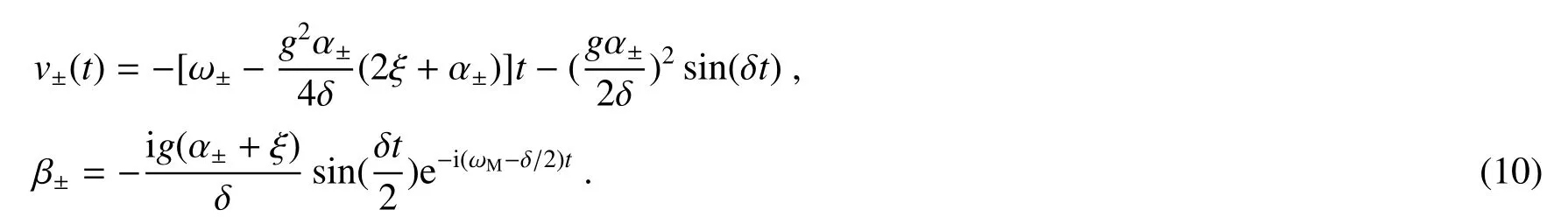
因此若设t=0时刻原子-腔的初态为任意态,力学振子处在真空态,即

则由(9)式可得t时刻系统的演化波函数为
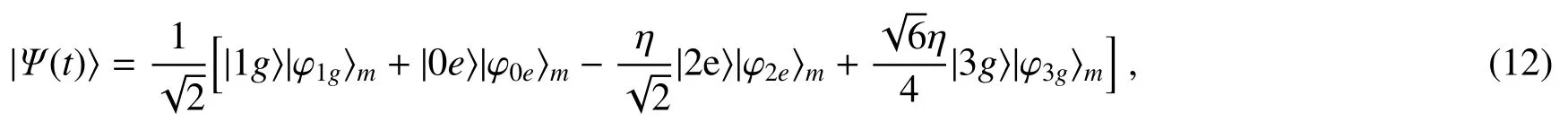
式中
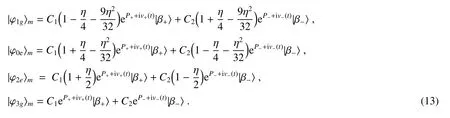
可以看出,|φ1g〉m、|φ0e〉m、|φ2e〉m、|φ3g〉m为宏观量子叠加态。若对腔进行测量,测得光腔中有0个光子,则力学振子状态为|φ0e〉m;若光腔中有1个光子,则力学振子状态为|φ1g〉m,若光腔中有2个光子,则力学振子状态为|φ2e〉m;若光腔中有3个光子,则力学振子状态为|φ3g〉m。不管测量结果如何,力学振子都将处在宏观量子叠加态。由(13)式可以看出,光子数为2或3的几率和光子为0或1的几率比值正比于η2,而此处假设η的大小为0.1的数量级,所以相比而言,光子为0或1的几率比光子数为2或3的几率高出两个数量级,所以下文仅对光子数为0或1的情况进行讨论。下面以|φ0e〉m为例进行讨论,其他三个态与此讨论结果相类似。
4 宏观量子叠加态的量子特性分析
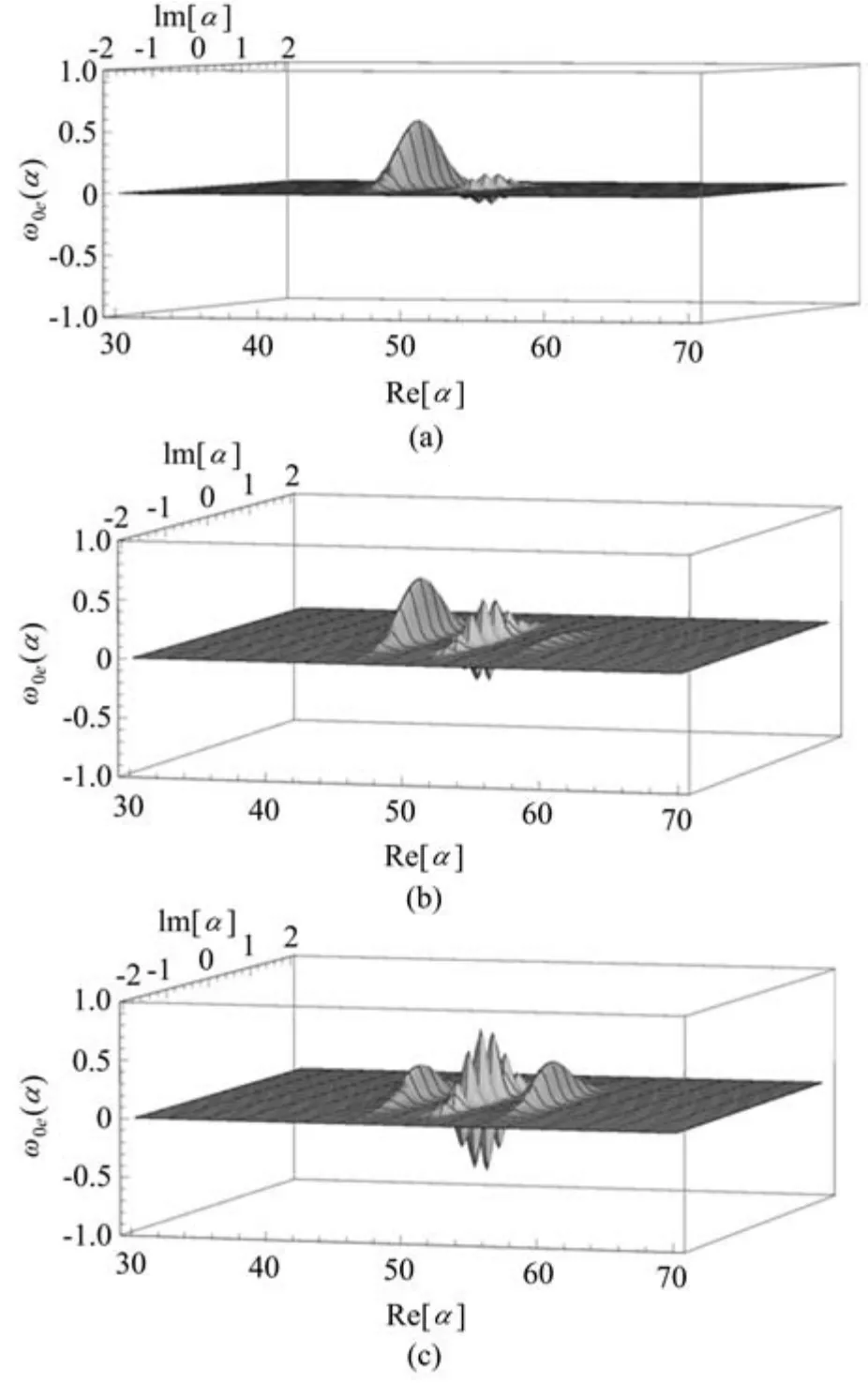
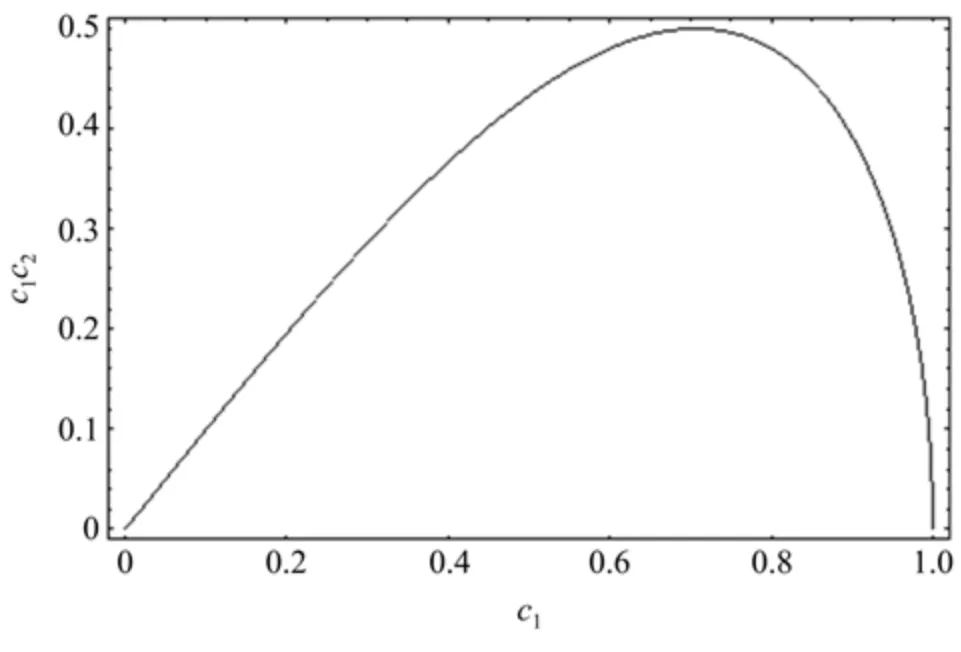
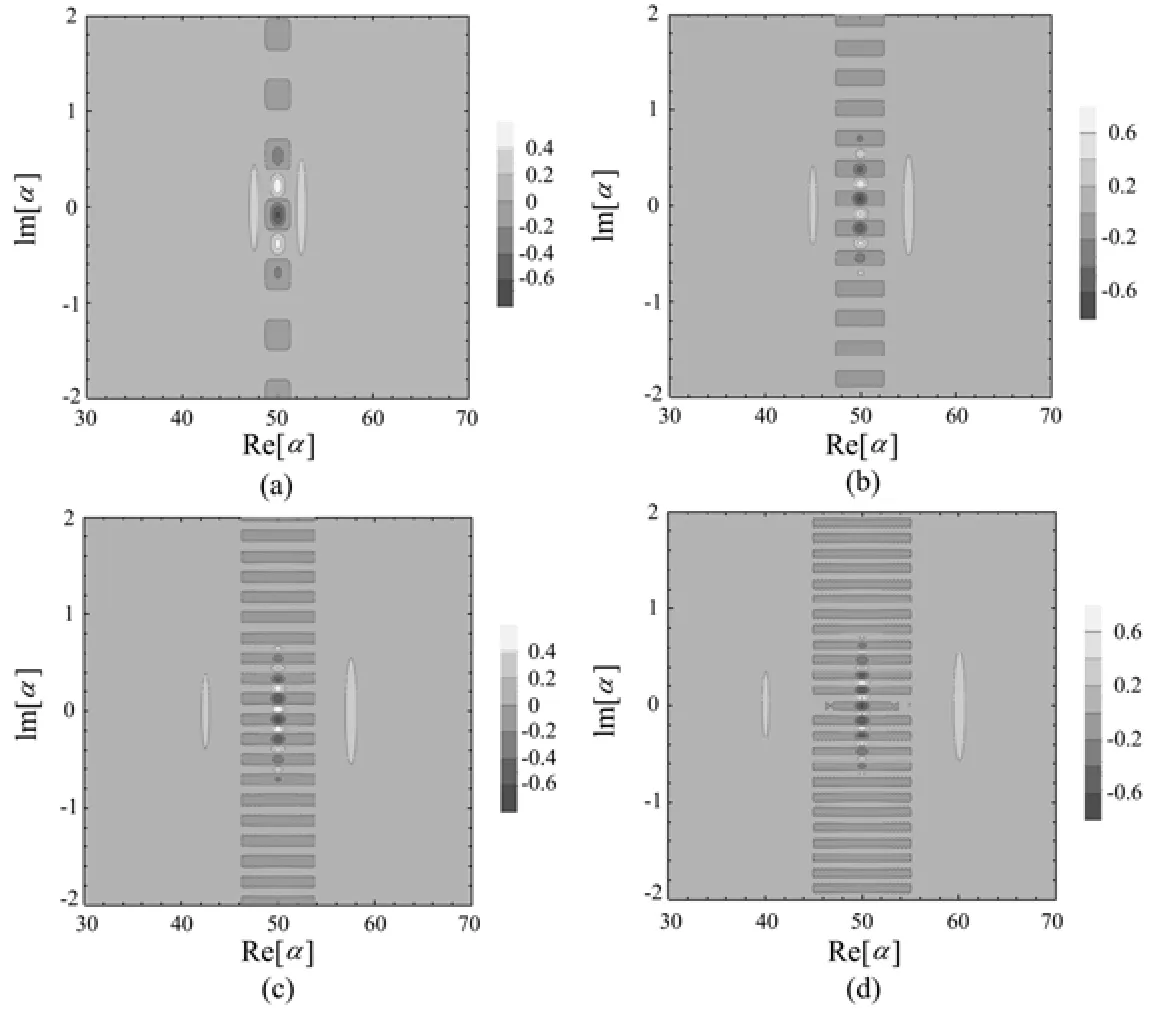
宏观量子叠加态的可分辨性由两个因素决定,|β±|max>1以及〈β+|β−〉≪1。且当t=(2k+1)π/δ(k取非负整数)时,β±取到最大值[15]。从(10)式可以看出,|β±|max=g(α±+ξ)/δ,因此若|β±|max>1,则需要满足条件δ 利用Wigner函数来讨论制备的力学振子宏观量子叠加态量子相干性的强弱。由Wigner函数的定义 式中α为任意复数,可得 考虑到二阶近似,计算得 式中Re函数为对复数取其实部。 从(16)式可以看出,|φ0e〉m态的量子相干性主要与第三项有关,当系统其他参数不变,该项取值与C1C2的乘积大小有关,因此量子相干性与原子-腔的初始态有关。图1中给出了几种不同原子-腔初态情况下|φ0e〉m的Wigner函数W0e(α)的示意图,以展示|φ0e〉m的量子相干性的强弱与原子-腔的初始态的相关性,图中Im函数为对复数取其虚部。图2给出C1C2随初始态系数C1的变化关系图,可以看出当时,C1C2的取值最大,即此时对应的原子-腔初态所制备出的力学振子的宏观量子叠加态的量子相干性最强。 图1 不同初始态下|φ0e〉m的Wigner函数示意图,ωM/g=20,δ=0.01g,t=π/δ,η=0.2。(a)C1=0.1;(b)C1=0.3;(c)C1=1/Fig.1 Schematic diagram of Wigner function of|φ0e〉m for different atom-cavity states,ωM/g=20,δ=0.01g,t=π/δ,η=0.2.(a)C1=0.1;(b)C1=0.3;(c)C1=1/ 图2 C1C2随着C1的变化,ωM/g=20,δ=0.01g,t=π/δ,η=0.2Fig.2 Relation curve of C1C2 varying with C1,whereωM/g=20,δ=0.01g,t=π/δ,η=0.2 此外,从(16)式还可以看出,|φ0e〉m态的量子相干性还与原子-腔的耦合强度η有关,因为函数形式较为复杂,在图3中给出η取不同值的情况下,|φ0e〉m的Wigner函数的等高线示意图。可以看出η的值越大,|φ0e〉m的两个波包的相干强度越强。 图3 η取不同值情况下,|φ0e〉m的Wigner函数的等高线示意图,C1=1/√,ωM/g=20,δ=0.01g,t=π/δ。(a)η=0.1;(b)η=0.2;(c)η=0.3;(d)η=0.4Fig.3 Contour plot of Wigner function for state|φ0e〉m with different values ofη,with C1=1/,ωM/g=20,δ=0.01g,t=π/δ.(a)η=0.1;(b)η=0.2;(c)η=0.3;(d)η=0.4 主要讨论了在原子-腔超强耦合光力系统中,利用对光力耦合的调制制备力学振子的宏观量子叠加态。所制备的宏观量子叠加态的两波包之间的量子相干性,其强弱与原子-腔的初始状态以及耦合强度密切相关,给出了宏观量子相干性最强的初态参数,并且发现耦合强度越强,宏观量子叠加态的量子相干性就越强。给出了|φ0e〉m的Wigner函数的解析表达式,从理论上明确体现了两波包的量子相干项,可以结合具体的实验参数分析Wigner函数的分布情况,继而讨论利用该方案所制备的宏观量子叠加态两波包之间的量子相干性情况,为相关的实验研究提供了一定的理论参考。

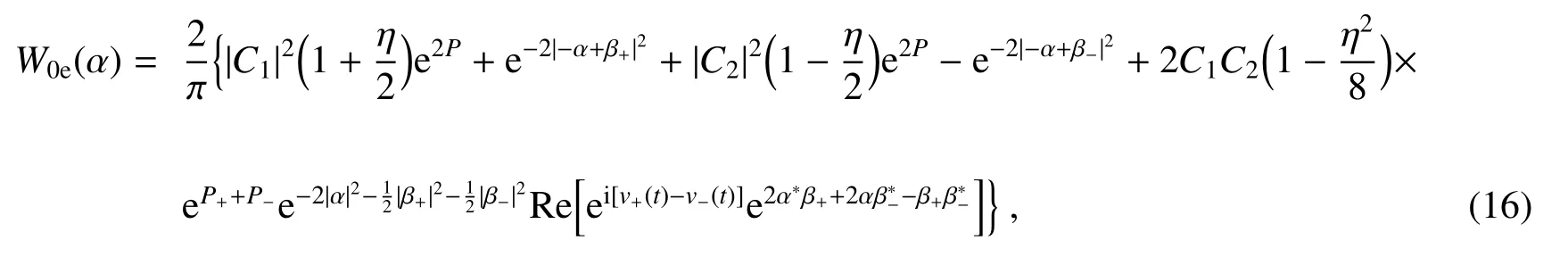
5 结论
