离子低能电子态的计算和光谱研究
2022-08-22王泽育崔琪和小虎卢丹华邱选兵何秋生赖云忠李传亮
王泽育,崔琪,和小虎,卢丹华,邱选兵,何秋生,赖云忠,李传亮
(太原科技大学应用科学学院,山西 太原 030024)
0 引言
20世纪90年代中期,高分辨率脉冲场电离零动能光电子能谱技术用于电子态的研究[11−13]。Cockett等[11]以偶对称性的里德堡态为中间态,采用共振增强多光子(2+1′)电离技术,得到了X2Πg电子态的振动平衡常数ωe以及ωeχe。此后,他们再次将B3Π0态设为中间态,用(1+2′)方案观测到了更加完整的振动光谱,并重新确定了X2Πg态的振动平衡常数ωe和ωeχe[12]。更进一步,他们第一次得到了第一电子激发态(A2Π3/2,u和新的电子态的振动能级结构[13]。直到2012年,Deng等[14]利用光外差速度调制光谱技术观察到12060∼13100 cm−1范围内转动分辨的吸收光谱。2017年,的光谱范围进一步扩展到11860∼12060 cm−1[15]。
1 计算方法
1.1 势能曲线和振转能级
为了提高势能曲线计算的准确性,需要考虑核价相关的影响[19]。碘的核价相关性主要来源于semi-core壳层4s4p4d,该壳包含在非活性空间中,不经过冻芯处理。相应地,采用了用于核价相关的wCVTZPP基集。PEC的计算在接近X2Π和A2Π态最小值的核间距处的计算步长为0.002 nm。其他区域采用较大的步长(核间距离为0.2∼0.65 nm)。X2Π和A2Π的SO耦合常数也采用相同的基集计算。此外,计算中还确定了A2Π3/2,u−X2Π3/2,g系统的电子TDMs。LEVEL程序可用于求解双原子分子的径向薛定谔方程[20]。利用它可以求解到电子态的振动波函数和振动能级。最后,X2Π3/2,g、X2Π1/2,g、A2Π3/2,u和A2Π1/2,u子态的分子常数,包括谐波频率ωe、一阶非谐系数ωeχe和在平衡核间距Re处的转动常数Be以及振-转耦合常数αe是用非线性最小二乘拟合的振动能级确定的。
1.2 谱线强度和爱因斯坦A常数
两个电子态的不同振子能级之间的跃迁线强度Sυ′,υ′′,J′,J′′与对应的(无旋转)TDM矩阵元的平方成正比[21,22],即

式中:R是核间距;ψυ′′,J′′(R)和ψυ′,J′(R)分别是基态和激发态的振转波函数;ℜe(R)是电子TDM,可表示为

式中:ri为电子坐标,ψel(R,ri)为电子波函数,µ(R,ri)为电偶极矩算符。利用有效势能函数(Veffect)可得到(1)式中的振动波函数,Veffect可以使用RydbergKlein-Rees(RKR)方法[21]或仅从从头计算得到。此处使用参考文献[15]报道的平衡光谱参数通过RKR1程序构造了A2Π3/2,u和X2Π3/2,g态的有效势能函数[23]。由(2)式,通过LEVEL程序利用两个低能的Ω子态(A2Π3/2,u和X2Π3/2,g)的势能曲线和由高精度从头计算得到的电子TDM产生TDM矩阵元。Honl-London因子是结合了无旋转的TDM矩阵元(见上文)在PGOPHER程序中产生的。
爱因斯坦A系数可通过PGOPHER程序获得,表示为[24]

式中线强度Sυ′,υ′′,J′,J′′是对上、下态的简并M分量求和,即
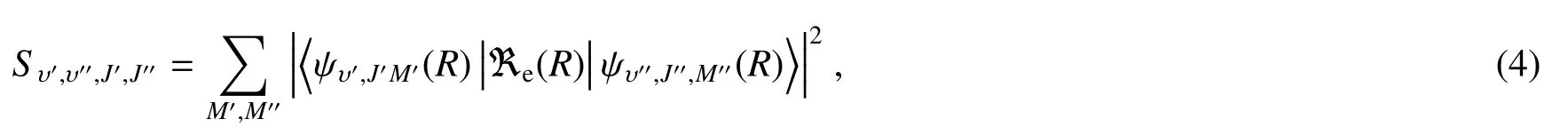
通过求解一个激发电子态的振动能级的所有可能(向下的)跃迁的爱因斯坦A系数和的倒数,可以得到该能级的辐射寿命。
1.3 预解离和无辐射寿命
双原子分子的PECs中可能存在势垒或双势阱结构。分子可以以一定的概率通过双势阱绝热势垒从一个非绝热态穿越到另一个非绝热态。当分子的能量低于势垒但高于解离极限时会发生预解离,使分子的寿命缩短。隧穿系数γ定义为

式中τd为预解离寿命,可表示为[25,26]

式中:τ0和m分别是分子的振动周期和质量,U(R)和E分别是振动能级的PEC和能量。τ0与势垒的宽度Γb相关(单位:cm−1),可表示为[27]

式中c为光速。
2 结果和讨论
2.1 Ω态的势能曲线和光谱常数
此处计算包含I+2的24个Λ-S电子态。这些电子态是由I+的3Pg基态和I的2Pu基态组合而成的。图1(a)展示了第一解离极限[I+(3Pg)+I(2Pu)]的二重态PECs。为了简洁,四重态未在图中体现。X2Πg和A2Πu态的平衡核间距分别为0.26 nm和0.29 nm。在平衡核间距处基态(X2Πg)的主要组分为···,第一激发态(A2Πu)由一个电子从6πu跃迁到6πg轨道形成。
在自旋轨道耦合的作用下,X2Πg电子态分裂为X2Π3/2,g和X2Π1/2,g子态,A2Πu电子态分裂为A2Π3/2,u和A2Π1/2,u子态,图1(b)展示了四个子态的PECs。X2Πg和A2Πu态的SO耦合常数为负。在平衡核间距处X2Π1/2,g和A2Π1/2,u分支的能量比其Ω=3/2分支分别高5842 cm−1和4740 cm−1。
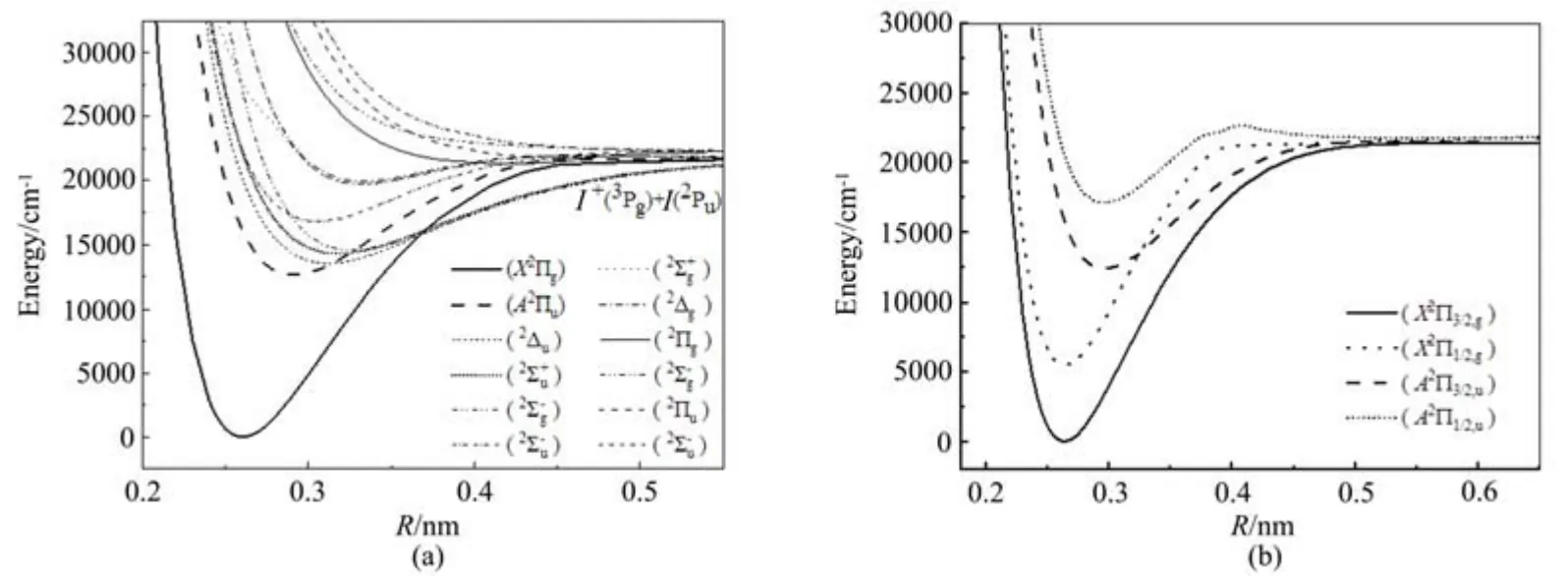
图1 (a)第一解离极限二重态的PECs;(b)SO作用下X2Πg和A2Πu态的PECsFig.1 (a)PECs of the doublet states of correlated to the first asymptote;(b)PECs of the X2Πg and A2Πu states in the presence of SO interaction
通过拟合PECs得到的光谱参数列于表1,并与已报道的计算和实验结果进行对比。通过取两个Ω子态能量的中间值,计算得到的A2Πu态的绝热激发能Te为12037 cm−1,这一结果明显高于参考文献[16]报道的值9603 cm−1。计算得到的X态的SO分裂值5482 cm−1比Li和Balasubramanian[16]报道的值(5979 cm−1)小497 cm−1,而计算的A态的值(4740 cm−1)比他们报道的值(5049 cm−1)小309 cm−1。计算得到的这四个态的Re、De(解离能)和ωe与文献[16]报道的结果吻合得不是很好,但是由于此处的计算中包含了大量的电子态,所以计算的值更接近实验值[17]。此次计算得到的Re和ωe值,和deJong等[17]报道的结果吻合得很好,当然X2Π3/2,g态的ωe值除外。X2Π1/2,g和A2Π3/2,u态的ωe值和Cockett等[13]报道的值一致,然而得到的ωeχe值明显小于他们报道的结果。计算得到的X2Π3/2,g和X2Π1/2,g态的解离能和振动能级ν=0的能量差值D0比文献[13]报道的对应值分别小1700 cm−1和2000 cm−1。对于X2Π3/2,g态,此次工作得到的Re、Be、αe和ωeχe参数与Deng等[14]通过高分辨光谱研究得到的结果相一致,然而ωe值符合得并不好。对于A2Π3/2,u态Re、Be和ωe值与文献[14]符合得很好,但是αe和ωeχe值却相差较大。
表1 能量最低的四个Ω态的光谱参数Table 1 Spectroscopic constants of the lowest four Ω states of
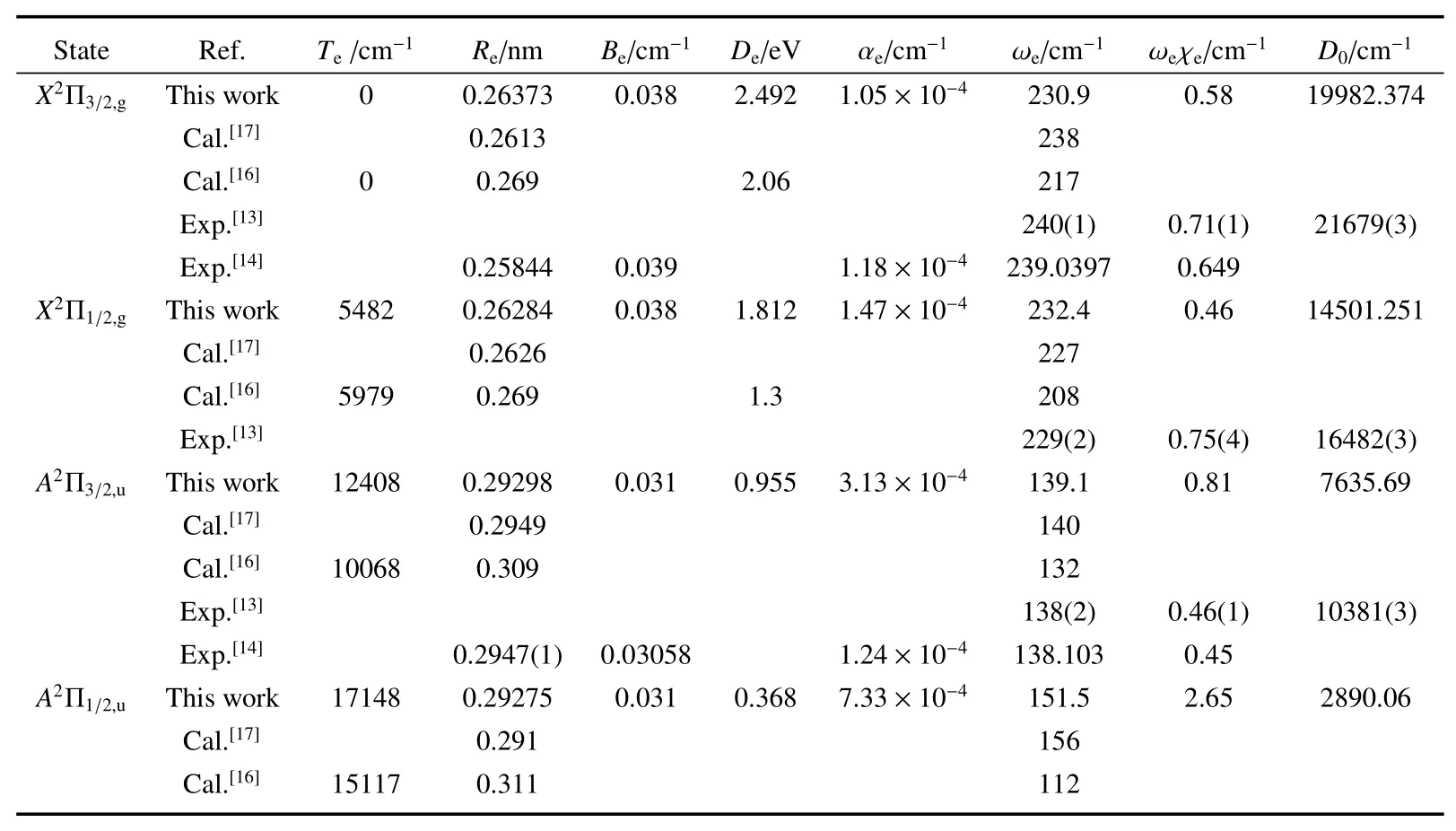
表1 能量最低的四个Ω态的光谱参数Table 1 Spectroscopic constants of the lowest four Ω states of
State Ref. T e/cm−1 R e/nm B e/cm−1 D e/eV αe/cm−1 ωe/cm−1 ωeχe/cm−1 D0/cm−1 X2Π3/2,g Thiswork 0 0.26373 0.038 2.492 1.05×10−4 230.9 0.58 19982.374 Cal.[17] 0.2613 238 Cal.[16] 0 0.269 2.06 217 Exp.[13] 240(1) 0.71(1) 21679(3)Exp.[14] 0.25844 0.039 1.18×10−4 239.0397 0.649 X2Π1/2,g Thiswork 5482 0.26284 0.038 1.812 1.47×10−4 232.4 0.46 14501.251 Cal.[17] 0.2626 227 Cal.[16] 5979 0.269 1.3 208 Exp.[13] 229(2) 0.75(4) 16482(3)A2Π3/2,u Thiswork 12408 0.29298 0.031 0.955 3.13×10−4 139.1 0.81 7635.69 Cal.[17] 0.2949 140 Cal.[16] 10068 0.309 132 Exp.[13] 138(2) 0.46(1) 10381(3)Exp.[14] 0.2947(1) 0.03058 1.24×10−4 138.103 0.45 A2Π1/2,u Thiswork 17148 0.29275 0.031 0.368 7.33×10−4 151.5 2.65 2890.06 Cal.[17] 0.291 156 Cal.[16] 15117 0.311 112
2.2 谱线强度和寿命
图2为计算得到的关于A2Π3/2,u←X2Π3/2,g系统的电子TDM随核间距变化的函数。它被用作生成不同振动带间的TDM矩阵元,而TDM矩阵元被用作计算A2Π3/2,u态振动转动跃迁的爱因斯坦A系数和υ=11−19振动能级的辐射寿命。计算的辐射寿命的值列于表2。目前,尚未见到有关电子态寿命的实验报道。

图2 A2Π3/2,u−X2Π3/2,g系统随核间距R变化的电子TDMFig.2 Electronic TDM of the A2Π3/2,u−X2Π3/2,g system asfunction of the internuclear distance R
表2 的A2Π3/2,u态振动能级的辐射寿命Table 2 Lifetime of vibrational levels of the A2Π3/2,u state of

表2 的A2Π3/2,u态振动能级的辐射寿命Table 2 Lifetime of vibrational levels of the A2Π3/2,u state of
Paremeter Value υ′ 11 12 13 14 15 16 17 18 19 τ/µs 2.29 2.18 2.22 2.15 2.20 1.88 2.32 2.38 2.42
2.3 实验谱的模拟与拟合
为了验证以上计算,利用计算出的分子常数和电子TDM函数,模拟了A2Π3/2,u−X2Π3/2,g系统转动分辨的光外差速度调制光谱。利用Voigt线型的二阶导数可以很好地再现实验光谱的谱线。将计算谱中的Lorentzian线宽和Gaussian线宽分别设为0.019 cm−1和0.026 cm−1以匹配实验谱线。在重建相对跃迁强度的过程中,确定了转动温度约为340 K,振动温度约为1500 K。
图3对比了I+2的A2Π3/2,u−X2Π3/2,g系统在12681∼13037 cm−1范围的吸收谱线与本研究得到的谱线,其中主要包含(13,1),(15,2),(14,1),(17,3),(16,2),(15,1),(18,3),(17,2)和(19,3)带的跃迁。模拟谱的整体强度轮廓与观测谱很接近,然而,在12920∼13037 cm−1范围内,由(17,2)带主导的模拟谱的跃迁强度一般比实验谱弱。这种差异是由于钛蓝宝石激光器在接近蓝限的高频区域激光稳定性不理想所致。在其他覆盖区域,模拟的跃迁强度与实验的跃迁强度匹配性很好。图4为计算谱线与实验谱线在12781.25∼12788.17 cm−1区域内的详细比较,可以看出仿真效果很好。
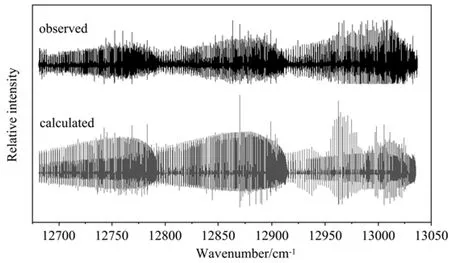
图3 在12681∼13037 cm−1范围光谱的观测谱(上)和计算谱(下)的对比Fig.3 Comparison of the observed(upper)and calculated(lower)spectra ofin the region of 12681−13037 cm−1
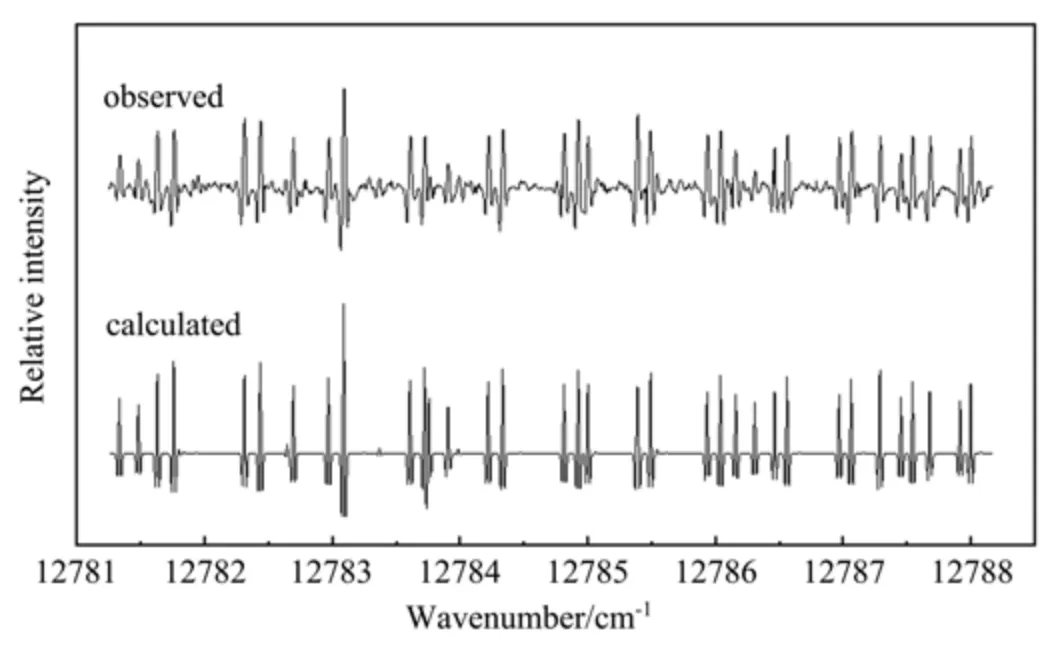
图4 在12781.25∼12788.17 cm−1范围观测谱(上)和实验谱(下)的转动光谱对比Fig.4 Rotational-resolved spectral comparison of the observed(upper)and calculated(lower)ofin the region of 12781.25−12788.17 cm−1
2.4 A2Π1/2,u态的预解离机制
由从头计算得到的电子态A2Π1/2,u的势能函数显示出了双势阱结构(见图5),第一势阱的深度(在较小的核间距0.295 nm处)大约5500 cm−1,而第二个势阱(在0.546 nm处)较浅,大约只有200 cm−1。图5绘制了A2Π1/2,u子态υ=0,υ=49和υ=58的振动能级和波函数,第二势阱的振动能级如插图所示。经计算,第一势阱和第二势阱的振动能级分别为46个和13个。第二个势阱的13个振动能级位于第一个势阱的υ=35和υ=49能级之间,υ≥49的能级高于解离极限。因此,这些态将预解离为I+(3Pg)和I(2Pu)。利用(6)式计算得到A2Π1/2,u态υ=49−58振动能级的预解离寿命(τd)值并列于表3。从(6)、(7)式可以看出,随着υ值的增加,τd迅速减少。当υ=58时τd值大约为10 ps。

图5 的A2Π1/2,u态的PEC、振动能级和振动波函数,插图为第二势阱的振动能级Fig.5 PEC,vibrational levels,and vibrational functions of the A2Π1/2,u state of.Vibrational levelsin the second potential well are shown in the inset
表3 的A2Π1/2,u态十个振动能级计算出的预解离寿命Table 3 Calculated predissociation lifetimes of ten vibrational levels of the A2Π1/2,u stateof

表3 的A2Π1/2,u态十个振动能级计算出的预解离寿命Table 3 Calculated predissociation lifetimes of ten vibrational levels of the A2Π1/2,u stateof
Paremeter Value υ 49 50 51 52 53 54 55 56 57 58 τd/s 1.63×1017 1.51×1010 5.35×104 27.4 9.50×10−2 4.65×10−4 3.61×10−6 3.77×10−8 5.27×10−10 1.06×10−11
3 结论
利用MRCI方法和核价相关的wCVTZPP基集,通过高精度的从头计算得到了的四个电子态X2Π3/2,g、X2Π1/2,g、A2Π3/2,u和A2Π1/2,u的势能函数,通过计算PECs推导出这些态的振动转动能级结构和光谱参数并与已有相关文献做了对比,对比结果令人满意。利用推导出的光谱参数再现了A2Π3/2,u−X2Π3/2,g系统高分辨的实验谱,并预测了激发态的爱因斯坦A系数和辐射寿命。最后对A2Π1/2,u态的预解离机制进行了分析,并计算了高振动能级(υ≥49)的预解离寿命,得到最高振动能级(υ=58)的预解离寿命约为10 ps。
