高空间分辨率关联成像技术研究

李能菲,黄 见

(1安徽职业技术学院机电工程学院,安徽 合肥 230011;2中国科学院合肥物质科学研究院安徽光学精密机械研究所,中国科学院大气光学重点实验室,安徽 合肥 230031;3先进激光技术安徽省实验室,安徽 合肥 230031)

0 引言

关联成像,或者称之为单像素成像、鬼成像,是一种新型的计算成像技术,其与传统面阵成像最大的不同在于其成像器件为桶探测器或者单像素探测器(非面阵探测器),如光电倍增管(PMT)、雪崩二极管(APD)等,鉴于单像素探测器具有光谱选择范围大、量子效率高等优势,使得关联成像技术在现有面阵探测器无法工作的波段具有潜在的成像优势,并成为前沿课题。

1995年,美国马里兰大学的科研人员首次基于纠缠光源方案实现了关联成像实验[1],因此,也有研究人员将关联成像称为量子成像,纠缠光源制备比较复杂,且对使用环境要求苛刻。而相对于纠缠光源,经典光源易于产生且应用广泛,研究人员尝试将经典光源应用于关联成像。2002年,美国罗切斯特大学的研究人员成功实现了基于经典光源的关联成像实验[2],研究证明经典光源也可以实现关联成像。传统的关联成像系统中,光源发出的光被分成两束,一束称为参考光路,一束称为探测光路。其中,参考光路的光在传播过程中不与成像物体接触,直接被面阵探测器接收,获取光强的分布;探测光路的激光与待成像的物体相互作用后被一桶探测器收集,获得与成像物体关联的信息。参考光路记录的光强分布与探测光路记录的信号经关联运算重建出目标物体图像。在此基础上,进一步研究发现：使用空间光调制器产生光强空间分布预置的调制光源可以省略参考光路,进而简化关联成像系统,推动了关联成像技术进一步向实用化方向发展。目前,关联成像技术在红外气体检测[3]、太赫兹成像[4,5]、光谱成像[6,7]、目标跟踪[8−10]、三维成像[11−13]等领域都展现了其广阔的应用前景。

另一方面,关联成像虽然具有众多的优势,但在空间分辨率与成像效率方面,与传统基于面阵探测器的成像技术相比仍有一定的差距。关联成像的成像机制导致了其空间分辨率与成像效率相互制约,在不失真的前提下,空间分辨率越高,成像所需的调制散斑越多,造成采集时间过长,不利于实际应用。因此,如何在低采样数的情况下,在保持较高成像质量的基础上获取更高的空间分辨率与帧频成为关联成像的研究热点[14]。文献[15,16]采用调制散斑编码复用的方法实现了多光谱关联成像,文献[17]采用散斑编码复用方法实现了同时对多个物体的成像与加密。本文将这种调制散斑编码复用的技术应用于高空间分辨率关联成像,即将具有编码信息的低空间分辨率散斑复用为高空间分辨率调制散斑,从而实现对高空间分辨率物体成像。

1 关联成像简介

常见的关联成像系统有两种基本结构,如图1所示,系统主要由光源、空间光调制器、成像物体和单像素探测器等部分构成。其中,图1(a)为前向调制或者主动调制结构的关联成像,光源投影到空间光调制器上,空间光调制器对照明光进行调制,被调制后的结构光与物体相互作用后,物体反射信号被单像素探测器收集;对于图1(b),光源(可以是自然光)发出的光对成像物体进行照明,物体反射的信号被空间光调制器接收,此时空间光调制器对物体反射信号进行调制,调制后的物体信号被单像素探测器接收,这种结构通常被称为被动调制或后向调制结构。可以看出,主动调制是对光源发出的照明光进行调制,而被动调制是对物体信号进行调制,这是两种结构的最大不同。

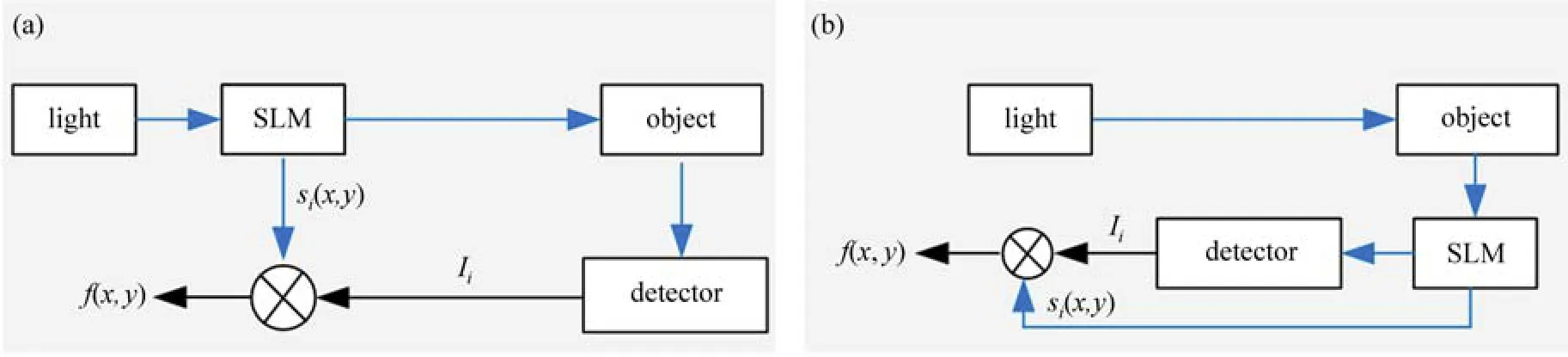
图1 关联成像基本结构示意图。(a)主动调制;(b)被动调制Fig.1 Schematic diagram of basic structure of ghost imaging.(a)Active modulation;(b)Slave modulation

无论是主动调制还是被动调制结构,当空间光调制器预置的调制信号为Si(x,y)时,单像素探测器接收的信号Ii可以表示为

式中f(x,y)表示待成像物体的图像,可以表示为

式中L为调制次数。(2)式为关联成像中常用的迭代复原算法,由(2)式可见,通常情况下,空间分辨率越高复原图像所需的调制次数越多,相应的采样时间就越长。

2 基于低空间分辨率调制散斑的高空间分辨率关联成像方法

一般情况下,在应用关联成像技术对空间分辨率为M×M的物体成像时,在不失真的前提下,至少需要M2个调制散斑,散斑数据量随空间分辨率提高呈平方关系急剧增加。在此采用多个编码的低空间分辨率调制散斑来实现M×M高空间分辨率的关联成像,为便于表述,假设将M×M空间分辨率的物体图像等分为4份,即P1:(1:N,1:N)、P2:(1:N,N+1:M)、P3:(N+1:M,1:M)和P4:(N+1:M,N+1:M),其中M=2N,通过获取4个(1:N,1:N)低空间分辨率的物体图像来重构M×M高空间分辨率物体图像。首先生成4个随机分布的大小为N×N的掩膜矩阵,分别记为EA、EB、EC和ED,掩膜矩阵满足

其中·表示点乘运算。从以上条件可以看出,4个掩膜矩阵为二值化正交矩阵,且在空间位置上不重合。计算机产生空间分辨率为N×N的二维调制散斑Si(x,y),调制散斑可以是随机的,也可以是基于Hadamard基或者傅里叶基产生的正交散斑,进而可构造出空间分辨率大小为N×N的4个调制散斑EA·Si(x,y)、EB·Si(x,y)、EC·Si(x,y)和ED·Si(x,y)。这4个调制散斑将分别对成像物体的P1、P2、P3和P4部分进行同时调制,单像素探测器接收成像物体的反射信号,表示为

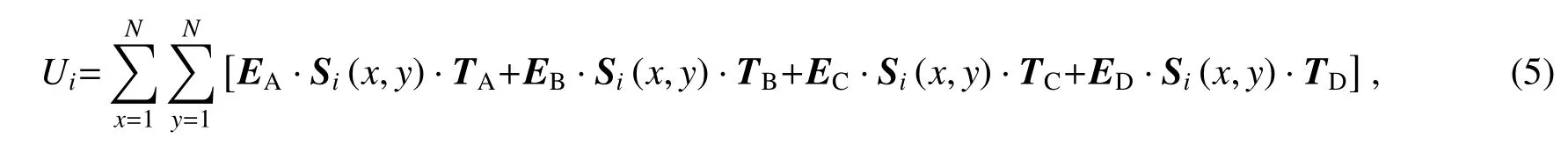
式中:TA、TB、TC和TD分别对应成像物体空间分辨率大小为N×N的4个子图像。(5)式可简化为

式中T表示空间分辨率为N×N成像物体的混叠图像,可表示为

对于(6)式的求解,一般情况下,因散斑Si(x,y)模式不同,求解(6)式的方法也不同。如果Si(x,y)为随机散斑,则一般通过压缩感知算法对T进行求解;如果Si(x,y)为基于Hadamard基的正交散斑,则可以通过迭代运算对T进行求解;如果Si(x,y)为傅里叶基散斑,则可以通过逆傅里叶变换的方法对T进行求解。在获取目标物体N×N分辨率的混叠图像T之后,根据掩膜矩阵EA、EB、EC和ED的正交性质,将掩膜矩阵分别与混叠图像T做点乘运算,可以得出成像物体的4个子图像fA、fB、fC和fD,即

得到的子图像fA、fB、fC和fD可以认为是TA、TB、TC和TD(待复原的全采样子图像)分别被掩膜矩阵EA、EB、EC和ED调制后的图像,相对于TA、TB、TC和TD,这里将fA、fB、fC和fD称为欠采样图像。这里应用组稀疏压缩感知图像算法[18]对(8)式进行求解,重构全采样图像TA、TB、TC和TD,即

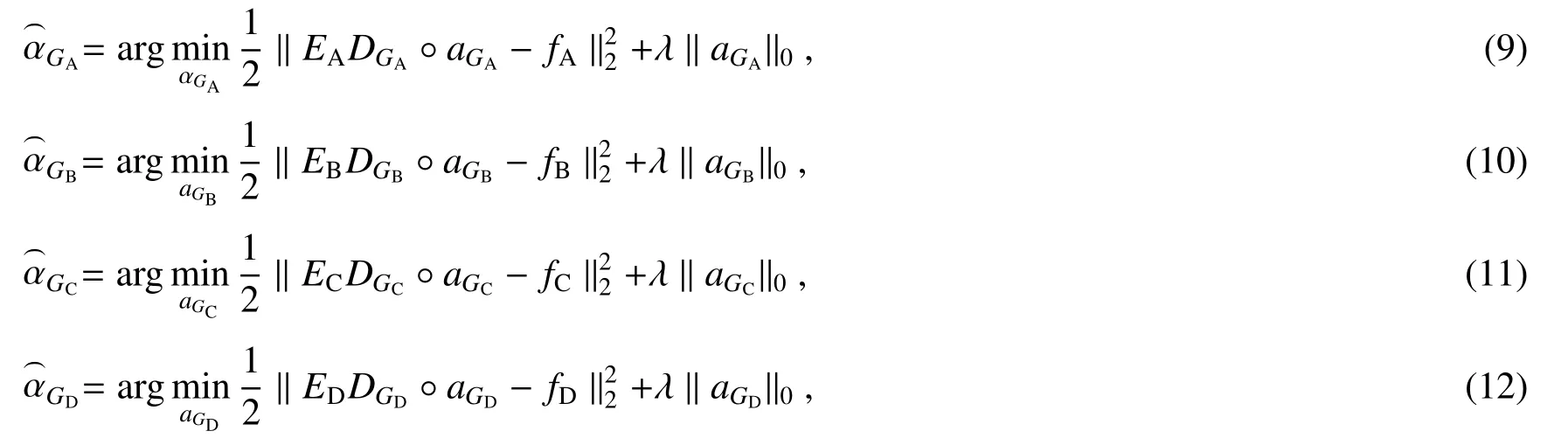
式中:λ为规则化参数,其根据欠采样的子图像质量进行调整,DGA、DGB、DGC和DGD分别为自适应学习得到的稀疏基,和为相应的稀疏系数,因此,全采样子图像分别通过和来重构,◦表示稀疏基和稀疏系数相乘运算。通过对全采样的低空间分辨率子图像TA、TB、TC和TD进行拼接来获得高空间分辨率成像物体图像。

3 仿真研究

上节理论介绍了通过多个低空间分辨率调制散斑来实现高空间分辨率关联成像的方法,本节将通过三个计算机仿真实验来验证此方法的有效性。仿真实验一的成像对象为二值化的空间分辨率为256×512的物体,包含4个“HPST”字母,可以将其分成2个分辨率为256×256的子图像,即P1:256×256的“HP”和P2:256×256的“ST”两部分。仿真计算的流程如图2所示:计算机生成65536个Hadamard基正交图案,如图2(a)所示;再同时构造2个分辨率为256×256的掩膜矩阵EA和EB,分别如图2(b)和2(c),且掩膜矩阵满足第2节介绍的约束条件;Hadamard基图案分别与掩膜矩阵点乘后生成2个256×256分辨率的调制散斑,如图2(d)和2(e),其将同时对256×512分辨率的物体进行成像[图2(f)];调制散斑对物体进行调制后,单像素探测器接收物体的信号并进行数字化,如图2(g)。由Hadamard基正交图案与探测信号经迭代运算[(2)式]可获得物体的混叠图像,如图2(h)。混叠图像与正交的掩膜矩阵进行点乘运算可分离出2个256×256分辨率的欠采样物体图像,如图2(i)和2(j),最后通过组稀疏压缩感知算法重构物体全采样图像,进而复现物体256×512空间分辨率的图像,如图2(k)所示。

图2 仿真计算流程图。(a)Hadamard基图案;(b),(c)掩膜矩阵;(d),(e)掩膜矩阵与Hadamard基图案点乘后的散斑;(f)成像物体;(g)调制散斑与物体相互作用后的单像素探测器接收的信号;(h)物体的混叠图像;(i),(j)欠采样的低分辨率物体图像;(k)重构的高分辨率物体图像Fig.2 Flow chart of simulation calculation.(a)Hadamard based patterns;(b),(c)Mask matrices;(d),(e)Results of dot product of mask matrix with Hadamard base pattern;(f)Imaging object;(g)The signal received by a single pixel detector from the modulated speckle interacting with the imaging object;(h)The mixed image of the imaging object;(i),(j)The undersampled low resolution images of the object;(k)The reconstructed high-resolution image of the imaging object

图3为对空间分辨率为256×512的物体仿真成像的结果。复原时对探测的信号按照绝对值从大到小排序,选取前25%、50%、75%、100%探测信号(对应散斑数分别为16384、32768、49152、65536)与其对应的Hadamard基图案进行计算。图3(a)∼(d)分别对应25%、50%、75%和100%采样下的复原结果。其中,图3(a)中最左边图像为复原的分辨率为256×256的物体混叠图像,其包含了成像物体的4个字母,但是无法区分开来,根据掩膜矩阵的正交性质,将掩膜矩阵与混叠图像进行点乘运算可分离出2个分辨率为256×256的子图像,如图3(a)中间列的两个图像,再对其分别应用组稀疏压缩感知算法重构全采样物体子图像,最后将其按照成像时调制散斑的排列方向进行拼接,从而复现成像物体高空间分辨率图像,如图3(a)最右列所示。

图3 仿真一的结果。(a)∼(d)分别对应25%、50%、75%和100%采样下的复原结果Fig.3 Results of the first simulation.(a)-(d)are the reconstructed results using 25%,50%,75%and 100%samples

为了定量评估所用方法重构图像的质量,这里分别采用信噪比(SNR,RSN)[19]和均方根误差(RMSE,ERMS)[20]来进行评估,可分别表示为

式中:N表示重构图像横向和纵向上的像素数;f(x,y)为空间位置(x,y)上的灰度值,f(x,y)max为图像f(x,y)中所有灰度值的最大值;f0(x,y)表示仿真使用的原始图像。RSN反应了复原图像的对比度,数值越大则表示图像的对比度越高。ERMS反映了复原图像与原始图像之间的误差,其值越小则复原图像质量越好,越接近原始图像。对上述仿真实验结果进行评价,计算的信噪比和均方根误差如表1所示,可以看出随着采样次数的提高,信噪比逐渐增大,而均方根误差逐渐降低,这种变化满足传统关联成像的图像复原规律。

表1 仿真一重构图像信噪比及均方根误差与采样数之间的关系Table 1 Relationship between the signal-to-noise ratio,root mean square error of reconstructed image with different measurements of the first simulation

下面开展对空间分辨率为512×512物体的仿真实验,仿真物体包含8个“12345678”数字,分上下两排,每排4个数字。采用所提出方法可以将其分成4个分辨率为256×256的子图像进行处理,即P1:(1:256,1:256)、P2:(1:256,257:512)、P3:(257:512,1:256)和P4:(257:512,257:512)四个部分,计算的流程和仿真一相似。计算机生成Hadamard基正交图案,同时构造4个分辨率为256×256的掩膜矩阵EA、EB、EC和ED,其满足第二节介绍的约束条件。掩膜矩阵分别与正交的Hadamard基图案进行点乘运算后,同时对成像物体的四个部分进行调制,单像素探测器收集物体的信号并进行数字化、存储。图像重构的方法与仿真一的处理方法相同,这里不再赘述。成像的结果如图4所示,图4(a)∼(d)分别对应25%、50%、75%(探测信号绝对值从大到小排序时的前16384、32768、49152个信号)和100%(全部信号)采样下的复原结果。从结果上可以看出,通过4个256×256低空间分辨率散斑同时对512×512空间分辨率的物体进行调制,可以较好地实现高分辨率成像。表2给出了仿真二图像重构的信噪比与均方根误差,相应变化规律与仿真一的相同。

表2 仿真二重构图像信噪比及均方根误差与采样数之间的关系Table 2 Relationship between the signal-to-noise ratio,root mean square error of reconstructed image with different measurements of the second simulation

从图3与图4可以看出,通过多个低分辨率的调制散斑同时对高分辨率二值物体进行成像,可以获得较好的成像结果。实际上,自然物体的图像均是多灰度级的,因此评估所提出方法对灰度物体的成像效果更有意义。图5给出了一组对512×512分辨率的灰度楼房仿真的结果,仿真使用的调制散斑、掩膜矩阵以及图像的复原过程均与仿真二的均相同,这里不再赘述。图5(a)∼(d)分别对应25%、50%、75%和100%采样下的复原结果。可以看出,通过四个256×256低空间分辨率散斑同时对512×512分辨率的灰度物体图像进行调制,也可以较好地实现高分辨率成像。表3给出了图像重构的信噪比与均方根误差,相应的变化规律与仿真实验二的相同。不过,通过对比表2与表3可以发现,在相同的采样数下,所提方法对灰度物体成像的信噪比与均方根误差较二值物体的差。

表3 仿真三重构图像信噪比及均方根误差与采样数之间的关系Table 3 Relationship between the signal-to-noise ratio,root mean square error of reconstructed image with different measurements of the third simulation

图4 仿真二的结果。(a)∼(d)分别对应25%、50%、75%和100%采样下的复原结果Fig.4 Results of the second simulation.(a)-(d)are the reconstructed results using 25%,50%,75%and 100%samples

图5 仿真三的结果。(a)∼(d)分别对应25%、50%、75%和100%采样下的复原结果Fig.5 Results of the third simulation.(a)-(d)are the reconstructed results using 25%,50%,75%and 100%samples

4 讨论与结论

关联成像机制决定了其成像空间分辨率与成像效率相互制约。通常情况下,横向空间分辨率越高,成像所需的调制散斑越多,从而造成采集时间过长,不利于实际应用。鉴于自然场景中图像具有稀疏性的先验知识,本文通过采用多个低空间分辨率的编码散斑来实现对高空间分辨率物体成像。技术上,通过构造多个低空间分辨率的掩膜矩阵与低空间分辨率的Hadamard基图案复用来生成高空间分辨率调制散斑对物体进行调制,单像素探测器收集高空间分辨率物体被调制后的信息。图像复原时,首先通过迭代算法复原出物体的混叠图像,然后利用掩膜矩阵相互正交的性质,通过物体混叠图像与掩膜矩阵点乘运算解调出相应欠采样的低分辨率图像,然后对分离出的欠采样图像应用组稀疏压缩感知算法复原全采样图像,最后复现物体高空间分辨率图像。计算机仿真验证了此方法的有效性。所提方法在对物体进行高空间分辨率成像且对采样时间要求比较苛刻的场合(X射线关联成像)有着重要的应用价值。

所提方法可以大幅降低调制散斑数量,进而减少在线采样时间。如对空间分辨率为512×512的物体进行成像时,使用基于正交Hadamard基的调制散斑,100%采样时需要散斑数量为262144(不考虑互补),在调制频率为20 kHz时,仅采集时间需要约13 s,而采用所提方法在相同条件下对空间分辨率为512×512的物体进行成像时,如果使用4个低空间分辨率的256×256调制散斑来成像,采集时间约为3.3 s;如果使用8个低空间分辨率的128×128调制散斑来成像,采集时间约为0.8 s,可以看出所提方法可以大幅降低采样时间。当然,本方法虽然大幅降低了在线采样时间,却以牺牲离线图像重构复原时间为代价,后期拟采用如卷积神经网络等人工智能算法来代替压缩感知算法,从而降低图像复原时间。