采用开关电感的Buck变换器CCM和DCM特性分析

祁静静 吴学智 王久和 续文政 刘京斗

采用开关电感的Buck变换器CCM和DCM特性分析

祁静静1吴学智1王久和2续文政1刘京斗1

（1. 北京交通大学国家能源主动配电网技术研发中心 北京 100044 2. 北京信息科技大学自动化学院 北京 100192）

Buck型DC-DC变换器采用开关电感单元后能拓宽电压变换范围且减小器件电流应力，但该文经推导发现，因电感的串并联切换会使等效电流分别为单电感电流的一倍和两倍，导致与负载电流的关系不确定，并使变换器变为非最小相位系统。该文以开关电感Buck变换器（SLBC）为例，在分析工作原理的基础上，指出该变换器在连续导通模式（CCM）下开关电感单元电流与负载电流间存在六种与电感和占空比密切相关的匹配关系，同时存在负调现象。在断续导通模式（DCM）下开关电感单元电流与负载电流间仅存在一种对应关系，且不存在负调现象。该文分别在CCM和DCM下使用状态空间平均法和全阶模型面积法建立SLBC的小信号模型，表明该变换器存在右半平面零点（RHPZ），系统特性类似于升压型DC-DC变换器。依据六种电流关系和RHPZ相对位置，给出电感、电容值的最佳选择区域，综合满足稳态纹波和动态响应需求。最后通过实验验证了该文理论分析的正确性。

开关电感 Buck 小信号建模 右半平面零点 参数设计

0 引言

如今在直流配电网、通信设备分布式电源系统及电动汽车等领域均需运用到宽范围DC-DC变换器[1-4]。通信设备分布式电源系统[2]因其经济性、环保性及灵活性而被广泛应用，其中可用宽范围DC-DC变换器代替传统体系结构中的总线变换器和负载点变换器，直接将48V的直流母线电压转换至5V或3.3V等负载所需电压。在电动汽车中，可用宽范围降压DC-DC变换器将72V电源转换成12V，供GPS、车灯及多媒体音箱等车载电器用电。

文献[5]中提出的开关电感（Switched Inductor, SL）单元因能拓宽电压变换范围且可减小器件电流应力而被众多学者用来设计宽范围降压DC-DC变换器。文献[6]直接将开关电感应用到小功率风能转换系统中，保证时刻从发电机获得最大功率，并为超级电容充电。也可将开关电感与其他降压DC-DC变换器结合，实现更宽范围的电压变换。文献[7]将传统Cuk变换器的中间级电容和后级电感分别用开关电容（Switched Capacitor, SC）和SL替代，使电压增益比传统Cuk变换器的缩小4-倍。文献[8]用开关电感代替传统Buck变换器中的电感，并在前级添加了开关电容，使电压增益减小了(2-)2倍。文献[9]将二次型变换器中后级电感使用SL，其电压增益能达到更低值。此外，开关电感具有高度对称性，便于应用磁集成技术[10]，使电流纹波或无源器件体积进一步减小，提高功率密度。

Buck和Forward变换器为最小相位系统，带宽较宽，可实现快速响应，而Boost、Buck-Boost及Flyback变换器为非最小相位系统[11-12]，存在右半平面零点（Right Half Plane Zero, RHPZ），这会使动态响应出现负调现象[13-14]，并限制变换器带宽和降低稳定性。文献[14]基于电压暂态模型优化电感/电容等电路参数，实现RHPZ抑制。三态Boost变换器[15]使电感电流增加一个自由流动状态，以此消除RHPZ。也可采用磁耦合[16]使Boost变换器在电感储能阶段仍可向输出端传递能量，从而抑制RHPZ。文献[17]在Boost变换器中引入开关电容，改变电容支路阻抗特性，提高变换器的动态响应性能。

现有开关电感的研究众多，但大都集中在拓扑设计方面，对其参数设计和系统特性研究较少，而本文经分析发现，基于开关电感的降压型DC-DC变换器在无源器件选择和系统特性方面与传统降压DC-DC变换器均有所不同。因此，本文以开关电感Buck变换器（Switched Inductor Buck Converter, SLBC）为例进行介绍，推导开关电感单元电流与负载电流关系，并分别采用状态空间平均法和全阶模型面积法建立连续导通模式（Continuous Con- duction Mode, CCM）和断续导通模式（Discontinuous Conduction Mode, DCM）的小信号模型，结合电流关系和RHPZ相对位置给出无源器件最佳选择区域，使SLBC具有更佳的稳态和动态特性。

1 SLBC时域分析

1.1 CCM工作原理

开关电感代替传统Buck变换器中的电感和二极管可构成如图1所示的SLBC拓扑结构，典型波形如图2所示。图中，i为输入电压，o为输出电压，i为输入电流，i1为电感电流，i为开关电感单元电流，i和o分别为输入和输出电容，1和2为等值电感，VD1和VD2为二极管且动作相同并与S1开关管互补。

根据图2a，对电感1(2) 列写伏秒平衡方程，可得CCM下电压增益CCM与占空比的关系为

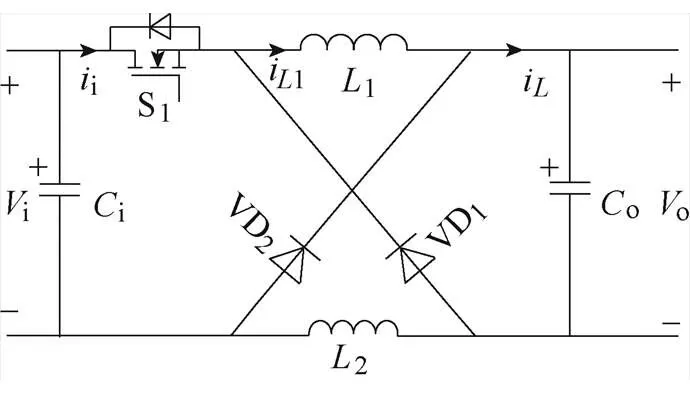
图1 SLBC拓扑结构

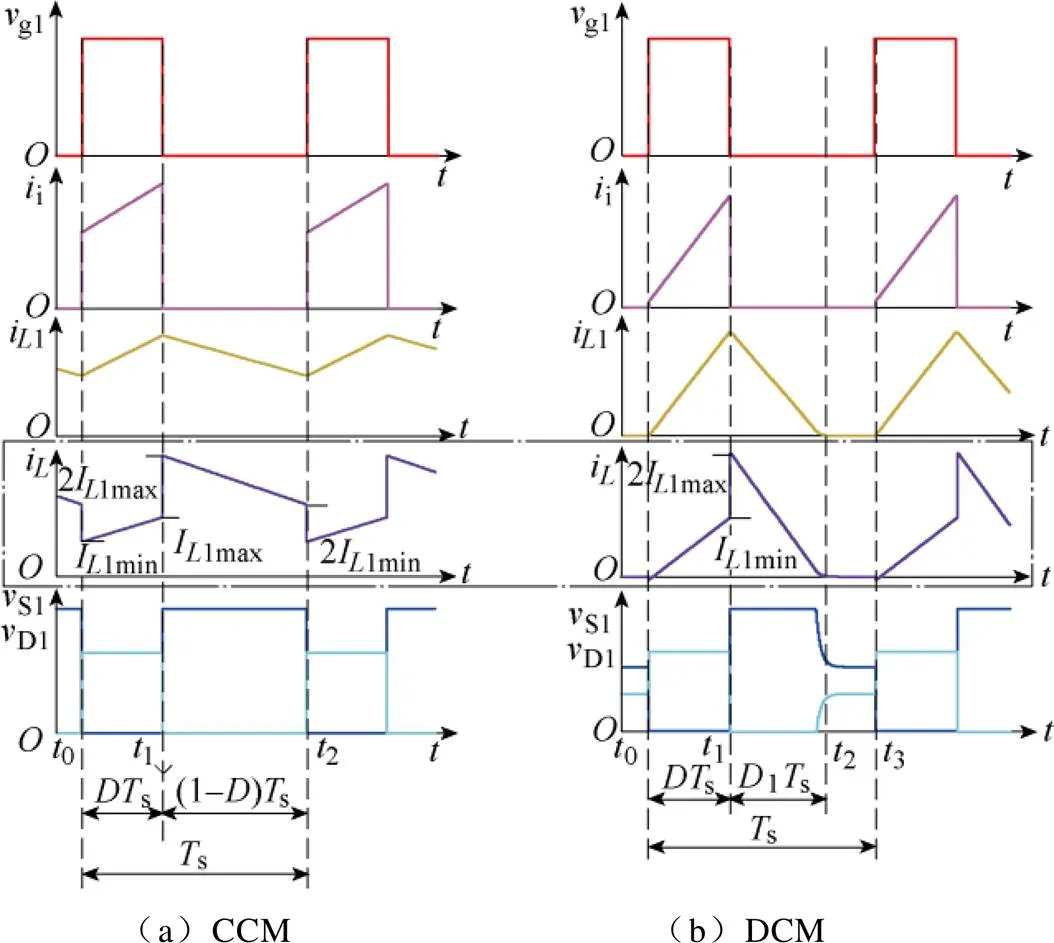
图2 典型波形

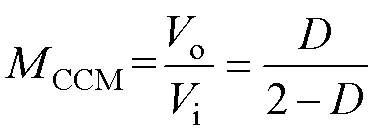
开关周期s内，输出电容o的电流满足安秒平衡，并结合负载电流o，则电感电流I1为

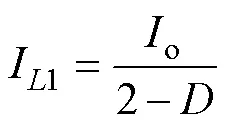
根据图2a，可知满足电感电流纹波Di1需求的电感1(2) 为

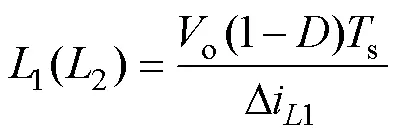
输出电容o的大小与通过它的充电电荷或放电电荷密切相关，而根据图2a可知，该值取决于开关电感单元电流I与负载电流o之间的相对大小，其中电感电流最大值I1max和最小值I1min分别为

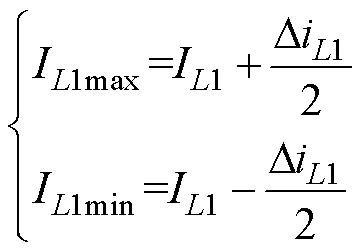
经分析，电流I1max、2I1min及o存在六种关系，见表1，且与占空比及电感1(2) 取值有关，电感1b0～1b3分别为

式中，为负载电阻。

表1 电流I1max, 2I1min及o间的大小关系

Tab.1 Relationship between the IL1max, 2IL1min and Io

电感1(2) 的串并联切换，使整个开关电感单元电流i不再像传统Buck变换器与负载电流o相等，而是在i1～2i1之间变化，导致输出电压纹波Do存在多种情况，进而影响输出电容o的设计。开关电感单元电流i与负载电流o（CCM）如图3所示。通过计算图3中阴影部分的面积，可得流过电容o的充电或放电电荷Di，如式（6）所示，再结合式（7）可用来设计满足输出电压纹波Do需求的电容o。

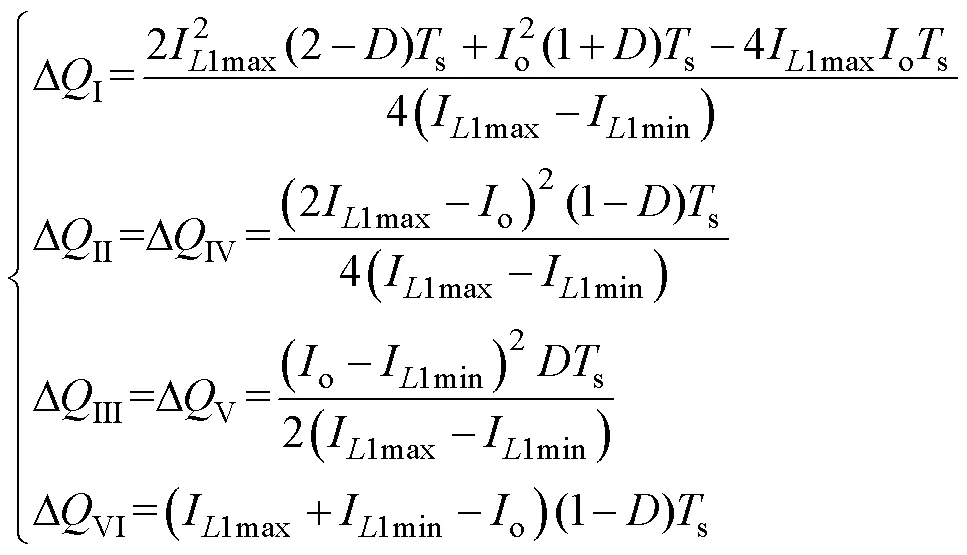
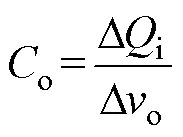
此外，开关电感单元的引入还会造成负调现象，占空比突增后对应的各电流的变化（CCM）如图4所示。为细化描述，称初值向下过程为初值欠冲，再次等于初值时为初值穿越[13]。电容电流io稳态时满足安秒平衡，而当占空比变为+时，开关电感单元电流i随之增加，但流入电容的电荷变化量小于其流出电荷变化量，使负载电流o（输出电压o）出现初值欠冲，当电容充电电荷增加较多时，负载电流o（输出电压o）开始增加，出现初值穿越。

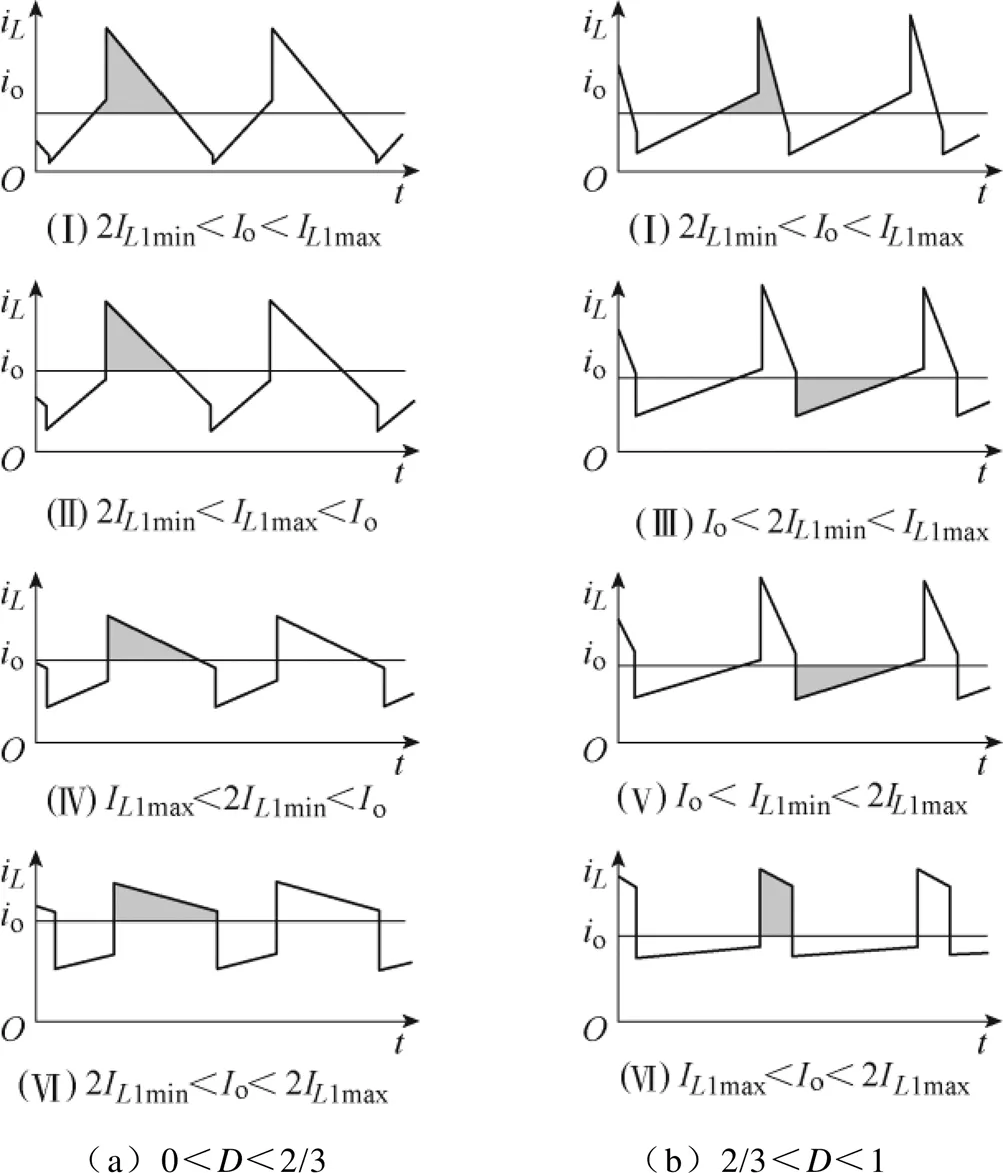
图3 开关电感单元电流iL与负载电流io（CCM）

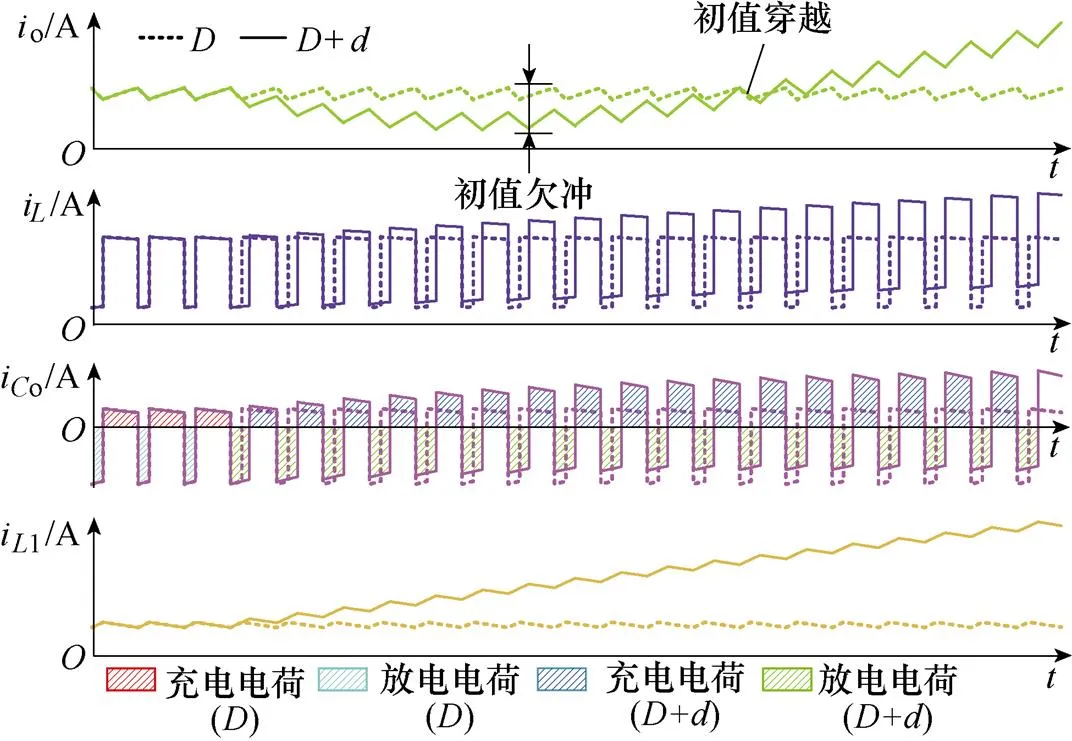
图4 占空比D突增后对应的各电流的变化（CCM）

SLBC出现负调现象，动态响应的瞬态变化与终值变化方向相反，闭环控制时可能引起正反馈，系统稳定性降低。下一步需对SLBC建模，从表达式中研究系统特性。

1.2 DCM工作原理

SLBC处于轻载时，会运行在DCM，对应的典型波形如图2b所示。同样对电感1(2) 列伏秒平衡方程，可得DCM下的电压增益DCM为

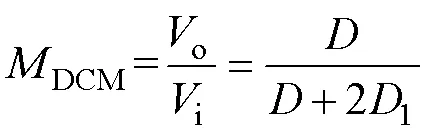
式中，1为电感电流续流阶段占空比。

DCM下的电感电流最大值I1max与电感电流纹波相等，即

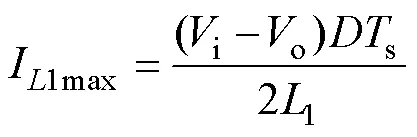
同时，输出电容o的电流在一个开关周期内仍满足安秒平衡，则根据图2b可得

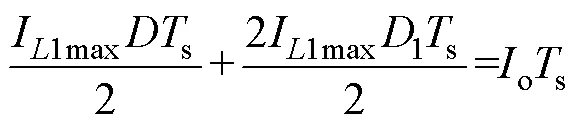
结合式（8）～式（10），可得电压增益DCM为

式中，=81/(s)。

根据式（10）和式（11），占空比1临界值为

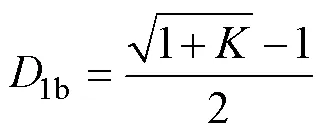
在一个开关周期内，电感电流i1积分的平均值等于电感电流平均值I1，则

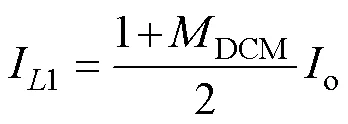
开关电感单元电流i与负载电流o（DCM）如图5所示。在DCM下，电流i与o只存在如图5所示o＜I1max一种关系。因为电感电流平均值I1还可写成

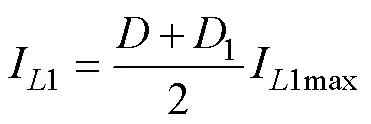
经化简，电感电流最大值I1max可表示为

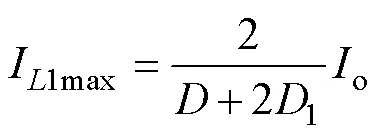
则电感电流最大值I1max的最小值I1max-min为

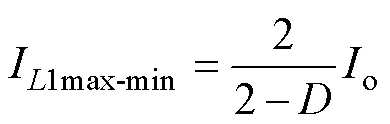
因此在DCM下，o＜I1max恒成立。

计算图5中阴影部分的面积，可得流过电容o的充电电荷D，如式（17）所示，同样结合式（7）可用来设计DCM下满足电压纹波需求的电容o。

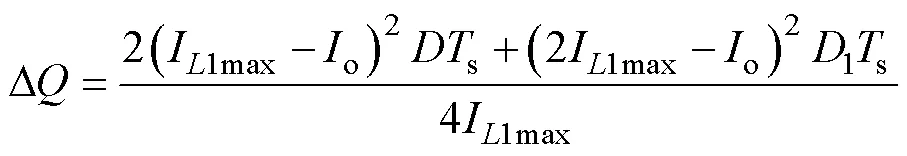
SLBC在DCM下无负调现象，占空比D突增后对应的各电流的变化（DCM）如图6所示，占空比增加时，瞬态电流iL增加，电容电流iCo也随之增加，使得负载电流io（输出电压vo）增加。

2 SLBC小信号模型

2.1 CCM下小信号建模

本节采用状态空间平均法对SLBC进行建模。电感和电容的寄生电阻R1、Ro也是重要的参数，尤其是输出电容o的寄生电阻Ro一般会引起一个零点，因此本节建模也将考虑寄生电阻的影响。

根据1.1节分析，得SLBC运行于CCM时的状态空间平均方程组为

对式（18）加小扰动进行线性化，并进行拉普拉斯变换，得到域表达式为

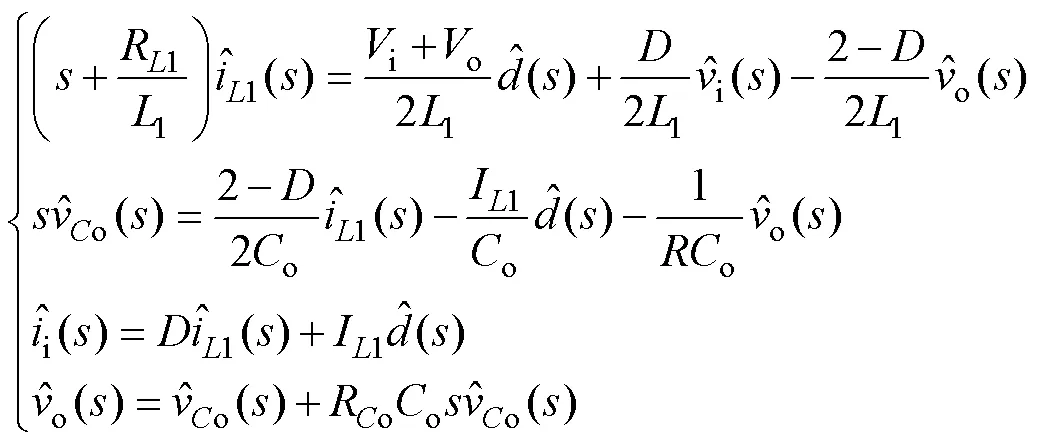
则CCM下控制-输出电压传递函数vd_C()为

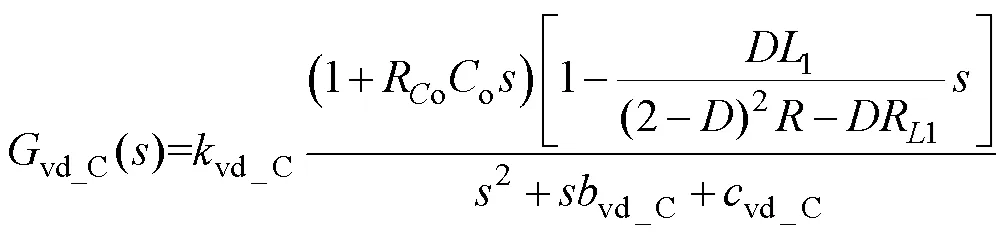
其中

可知vd_C()是二阶系统，并存在一个左半平面零点（Z1_C）和一个RHPZ（Z2_C）分别表示为

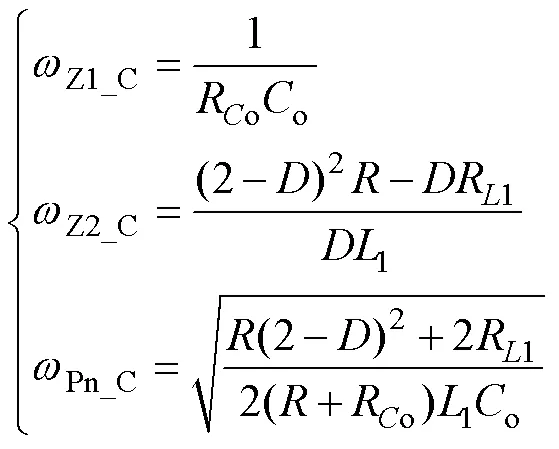
SLBC的vd_C()特性已发生改变，与Boost类似，为非最小相位系统，且其低频增益和双极点频率均与占空比有关，RHPZ与占空比、负载电阻、电感及其寄生电阻有关，与电容及其寄生电阻无关。

采用SLBC电路参数进行小信号仿真见表2，并将仿真结果与式（20）所示的理论结果进行对比，对比结果如图7所示，验证了理论建模的正确性。其穿越频率处对应角度 =-184°，已小于-180°，将会给闭环控制带来挑战。

CCM下零极点分布随占空比的变化如图8所示，随占空比减小，极点1_C和2_C向远离实轴方向移动，系统阻尼减小，其中谐振频率r_C和阻尼系数C如式（22）所示，当0.707＜C＜1时，无谐振峰值，本算例下C=0.284。左零点1_C仅与输出电容o和其寄生电阻Ro有关，右零点2_C向远离原点方向移动，且移动速率随占空比的减小而提升，这将有利于高降压比工况。

表2 SLBC电路参数

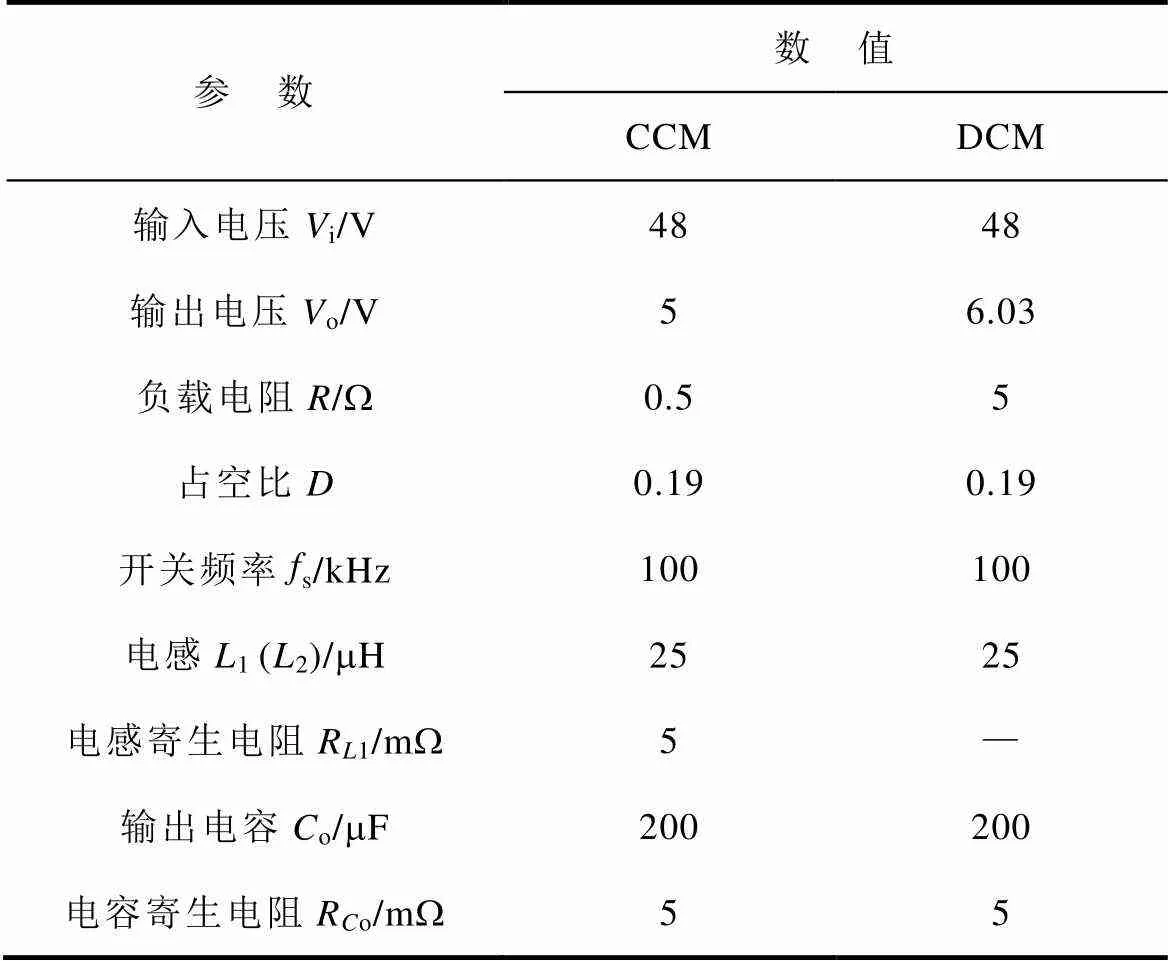
Tab.2 Circuit parameters of SLBC

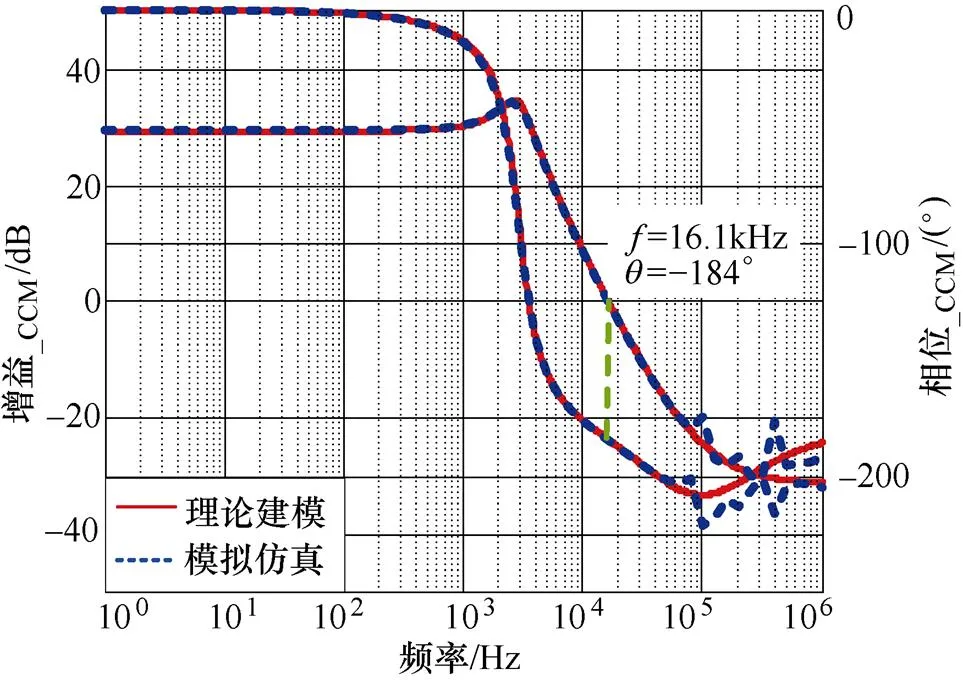
图7 Gvd_C(s)的Bode图__理论VS仿真（CCM）

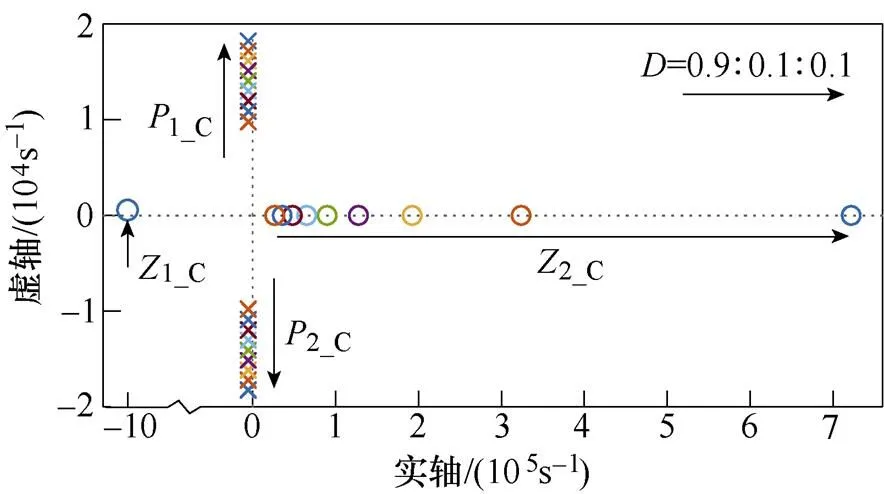
图8 零极点分布随占空比D的变化（CCM）

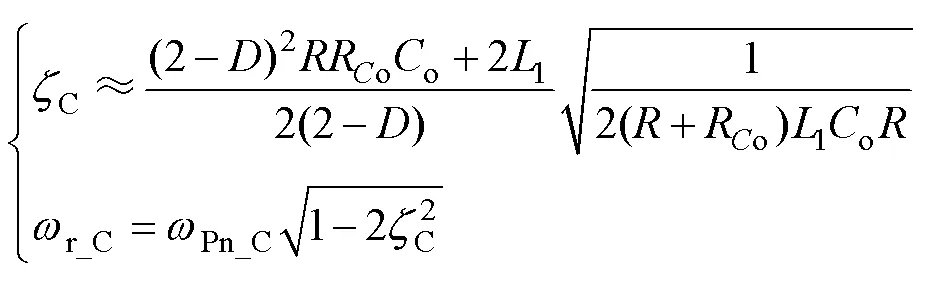
2.2 DCM下小信号建模

DCM与CCM相比，增加了一个未知数，即占空比1，若仍采用传统状态空间平均法中的用电感伏秒平衡表示占空比1，则会造成传递函数降阶，使相频特性曲线的准确度最多只有开关频率的1/10左右，不能反映高频特性。因此，本文采用全阶模型[18]中的电感电流平均值I1表示占空比1，即

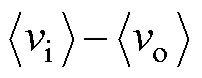
同时，虽然电感的寄生电阻会影响RHPZ大小，但与负载电阻相比较小，可忽略该参数，因此DCM建模中为简化分析仅考虑电容寄生电阻的影响。

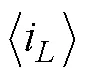
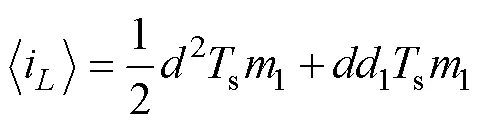
将式（23）代入式（24）并化简，可得

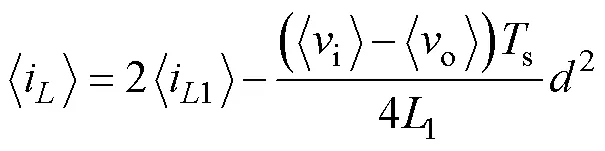
根据1.2节理论分析并结合式（24）和式（25），得SLCB运行于DCM时的状态空间平均方程组为

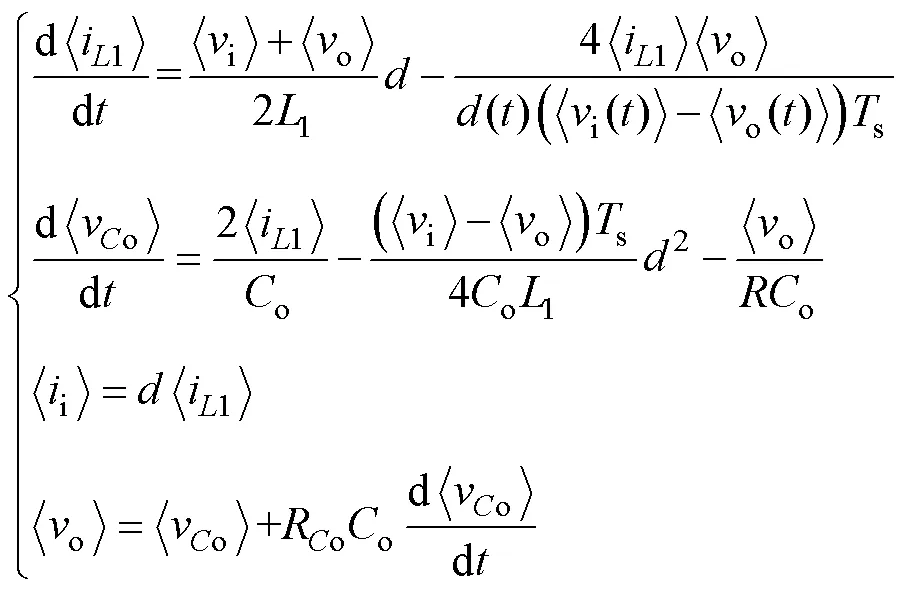
采用雅可比矩阵对式（26）进行线性化，并进行拉普拉斯变换，得到其对应的域表达式为

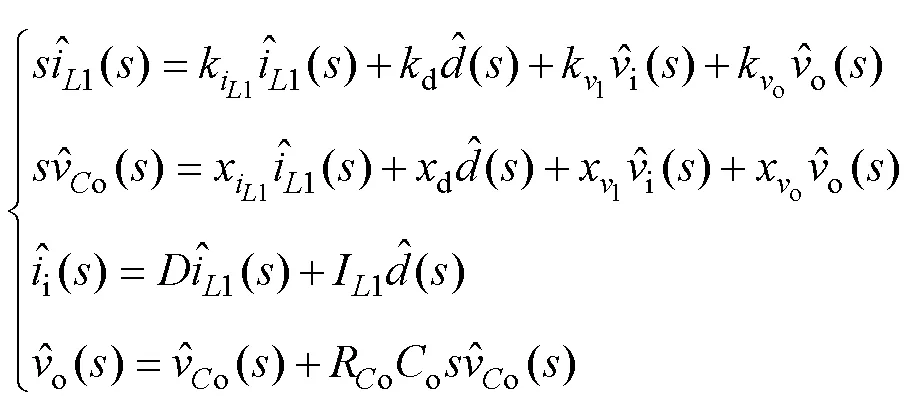
式中，系数k和x可参见附录式（A1）。

根据式（8）、式（11）及式（13），可将占空比、输出电压o及电感电流I1表示为

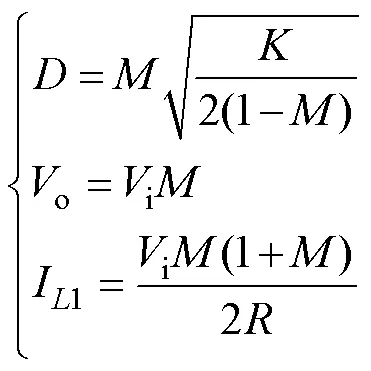
其中

=DCM

进而可得DCM下的vd_D()，如式（29）所示。本文采用的面积法与文献[18]最终的结果一致，但本文无需增加额外矫正矩阵，更加简洁明了，而且采用的面积法在CCM中与传统状态空间平均法等效。

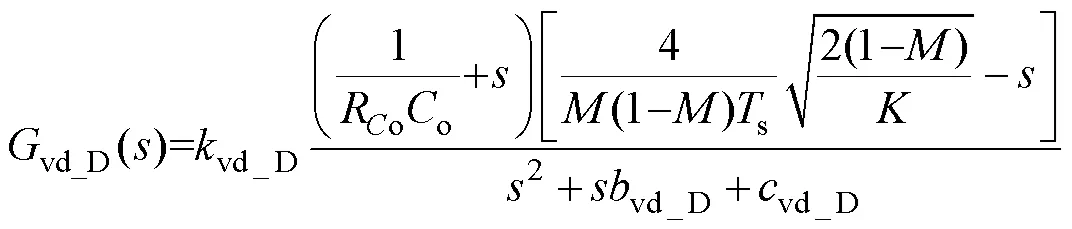
式中，系数vd_D、vd_D及vd_D可参见附录式（A2）。

可以看出，SLBC在DCM下仍存在一个RHPZ，即式（30）中的Z2_D。采用表2所示参数进行小信号仿真，并将仿真结果与式（29）所示的理论结果进行对比，对比结果如图9所示，可以看出本文采用的全阶模型面积法建模得到的幅频和相频特性曲线都更接近于实际值，而采用状态空间平均法建模得到的相频特性曲线存在严重误差。

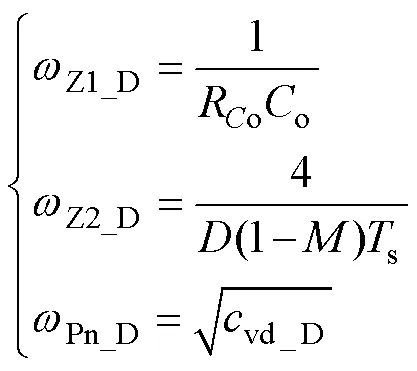
DCM下零极点分布随占空比D的变化如图10所示，随占空比D减小，极点P1_D和P2_D均在实轴上并向原点方向移动，为过阻尼系统，根据式（31）所示阻尼系数zD可得本算例下zD=5.97。零点随占空比D的变化与CCM时相同，但DCM时wZ2_D处对应的频率fwZ2_D已大于开关频率fs，使得有足够的相位裕度，该算例下q =-99°。这有利于控制环路设计，也促使占空比D变化后输出电压Vo无负调现象，对SLBC的动态响应和稳定性的影响较小。

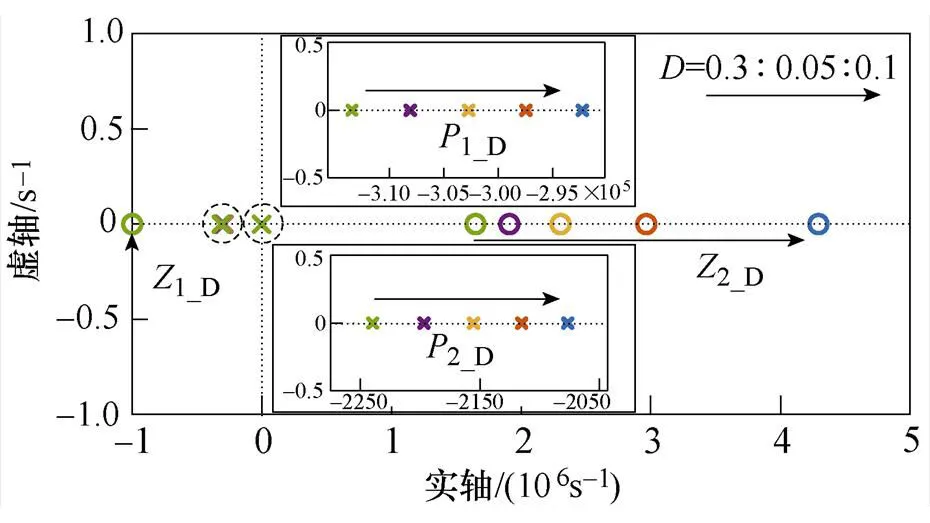
图10 零极点分布随占空比D的变化（DCM）

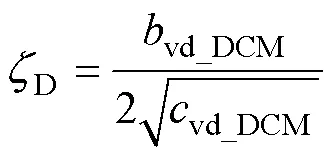
综上可知，SLBC在系统特性方面，极点频率与占空比有关，且存在一个RHPZ，为非最小相位系统。其中在CCM下该RHPZ会使剪切频率处无足够的相位裕度，将影响系统稳定性和动态响应速度，而在DCM下该RHPZ的影响已可忽略。

3 电路参数设计

根据上述建立的小信号模型可分析影响负调的电路因素。由于电感电容寄生电阻较小，为简化分析暂且忽略寄生电阻的影响。发生占空比变化D后，输出电压变量可表示为Do()=vd_C()D/。如当SLBC工作在过阻尼状态时，Do()可表示为

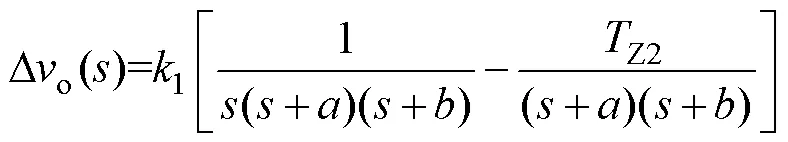
其中

通过拉普拉斯反变换，可得初值穿越时间c、初值欠冲峰值时间p及初值欠冲峰值Do(p)分别为

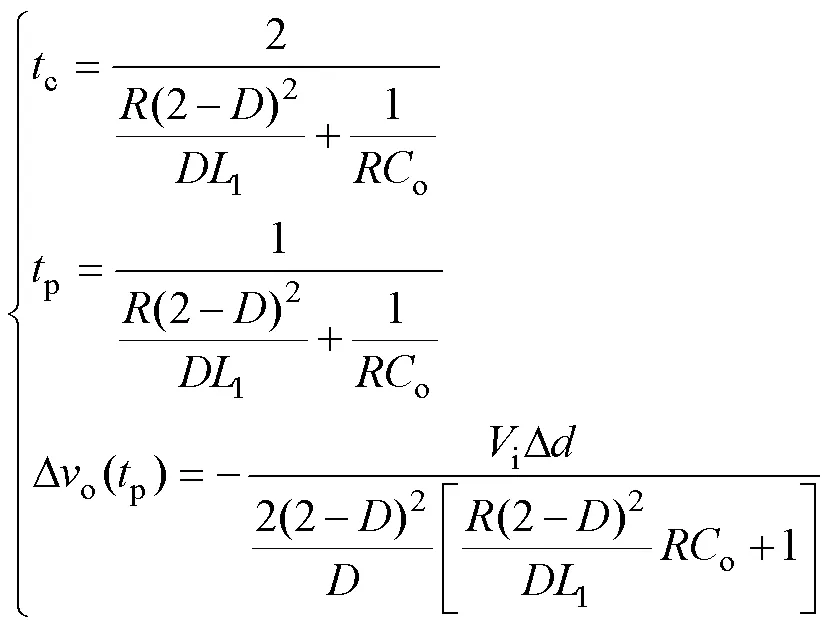
根据式（33）可知，SLBC在发生占空比突变时输出电压会有一个与终值相反的暂态变化，即对应图4所示的负调现象。若减小电感1，对应RHPZ角频率Z2_C增大，向远离原点方向移动，最终导致初值欠冲幅值Do(p)的绝对值减小，初值欠冲峰值时间p和穿越时间c也减小，类似其他参数的影响见表3。

表3 各电路参数对负调现象的影响

Tab.3 Effect of circuit parameters on negative regulation phenomenon

注：“↓”表示减小；“↑”表示增大；“→”表示远离；“←”表示靠近；“—”表示无影响。

负调现象是RHPZ的物理表现，表明在闭环控制时会造成正反馈以致系统不稳定。而从复平面角度一般要求剪切频率处要有足够的相位裕度，但RHPZ会使相位减少90°，如图7中相位已小于-180°，而通常会将系统带宽选择在RPHZ的1/5左右[19]，以此避免该零点造成的不稳定问题，但又会造成系统动态响应变慢。通过表3可知，负调现象和RHPZ都和电路参数密切相关，因此可选择合理的参数大小以优化系统的稳态和动态性能。

无源器件的设计要满足纹波需求，SLBC由于开关电感的存在使得输出端电感电流不再等于负载电流，而是由占空比和临界电感1i划分为DCM和CCMⅠ～CCMⅥ个区域，如图11所示，其中，CCMⅠ～CCMⅥ对应于表1所示六种电流关系。如CCMⅡ区域，仅存在于0＜＜2/3且1b1＜1＜1b3时，电流波形对应图3a_Ⅱ。

若要增加带宽，则需要RHPZ尽可能远离原点。根据式（21）已知，RHPZ对应角频率Z2_C，若RHPZ所处频率z大于s/2或s甚至2s，则电感1需满足式（34）要求。同时定义电感电流纹波系数=Di1/I1，并将各临界电感代入式（3），可知各区域临界电感电流纹波系数大小，如式（35）所示，对应关系如图12所示。

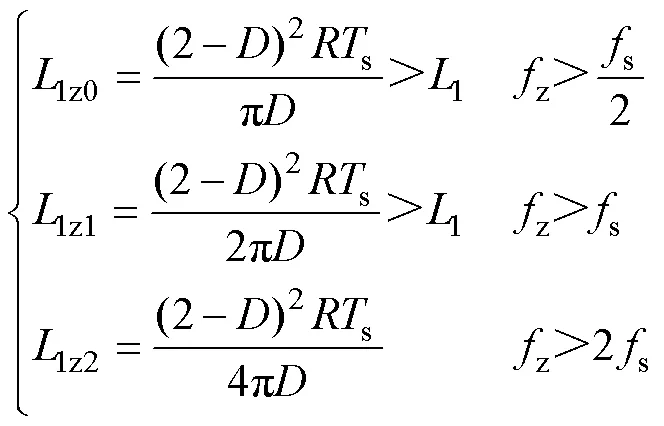
（35）

由图12可知，各区域对应的电感电流纹波范围，同样如CCMⅡ区域，2/3＜＜2(1-)，即该区域最小电感电流纹波系数也将大于66%，而过大的电感电流纹波虽会减小电感量，但存在磁饱和、铁损大、电感特性变化大及电容需求大等问题。因此，为减小电感量的同时避免上述问题，可在0＜＜2/3时，使选择的电感工作在CCMⅣ或CCMⅥ区域，在2/3＜＜1时，工作在CCMⅤ或CCMⅥ区域。

在上述基础上要提高系统动态响应，需使1＜1z0、1＜1z1或1＜1z2，临界状态如图12中虚线所示。可以看出若z＞2s，则电感量太小，纹波太大或者处于极限占空比处，难以满足；若z＞s，则仅当0.11＜＜0.25和0.86＜＜0.9时有合适电感取值，并分别工作在CCMⅣ和CCMⅤ区域；若z＞s/2，则在0.11＜＜0.9安全范围内电感均有合适取值，其中0.11＜＜0.53工作在CCMⅣ区域，0.53＜＜0.78工作在CCMⅥ区域，0.78＜＜0.9工作在CCMⅤ区域，如图12中虚线面积所示。

将各临界电感代入式（3）～式（7），可求满足输出电压纹波要求下所需电容大小。定义输出电压纹波系数=Do/o，标幺化电容pu=/s，可知各区域在满足相同输出电压纹波时所需电容大小，如图13所示。当电感为1z0或1z1时，需先根据图12判断所处区域，具体大小可参见附录。已知在一定占空比范围内能在满足电感电流纹波需求的前提下实现z＞s，但根据图13可知，由于电感量减小对应所需电容容量会明显增大，尤其当SLBC处于高降压比工况时。而要实现z＞s/2以提高响应速度时，不仅可在全占空比范围达到，其对应所需电容容量与原区域相差很小，使得电感电容取值选择较多。注意在CCMⅥ区域内，输出电容在s期间完全充电，在(1-)s期间完全放电，对应图3a_Ⅵ和图3b_Ⅵ，此时电容大小已与电感取值无关，因此在0.53＜＜0.78阶段内，pu（1=1z0）分别与pu（1=1b2）和pu（1=1b1）重合。

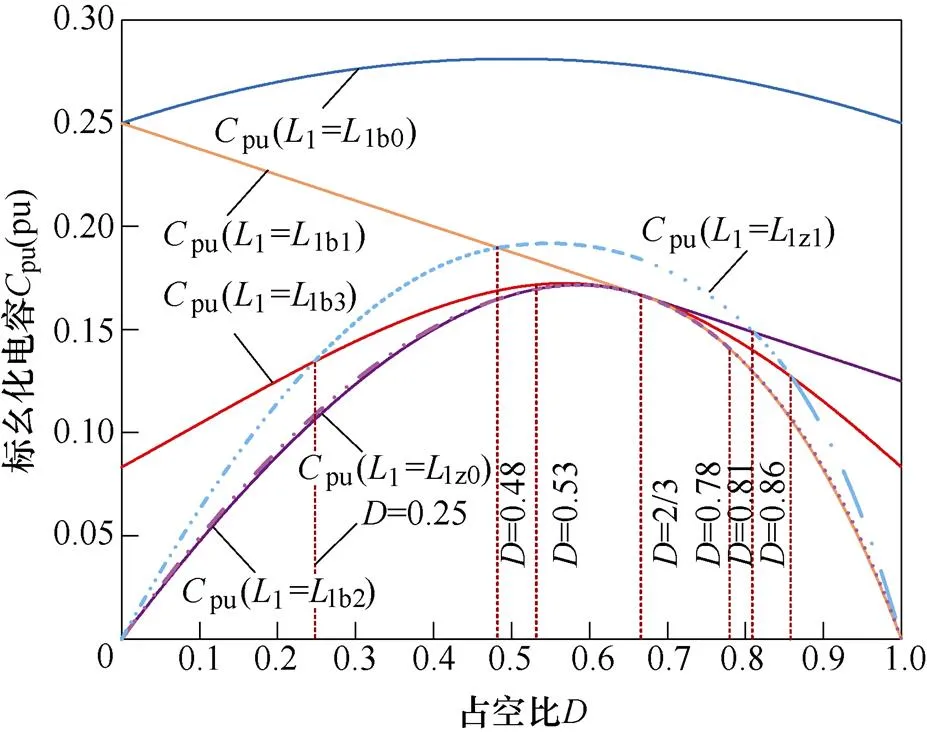
图13 相同输出电压纹波下所需标幺化电容

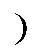
4 实验验证

本节将对电感电流与负载电流间关系，开环负调现象及闭环动态响应等进行相关实验验证。

图14展示了开环下0＜＜2/3时存在的四种电流关系。采用表2所示参数和1.1节关系公式可知，该算例下电感电流I1平均值为5.52A，负载电流o为10A，并根据表1可知对应电感临界值为1b0= 3.67mH、1b1=4.53mH、1b2=38.9mH、1b3=11.02mH。当电感1=7mH时，SLBC工作在CCMⅡ区域内，= 104.8%；当1=25mH时，工作在CCMⅣ区域内，= 29.3%。证实不同电感取值会使开关电感单元电流与负载电流存在不同关系，使传输到输出端电容能量形式不同，影响输出电容的设计。

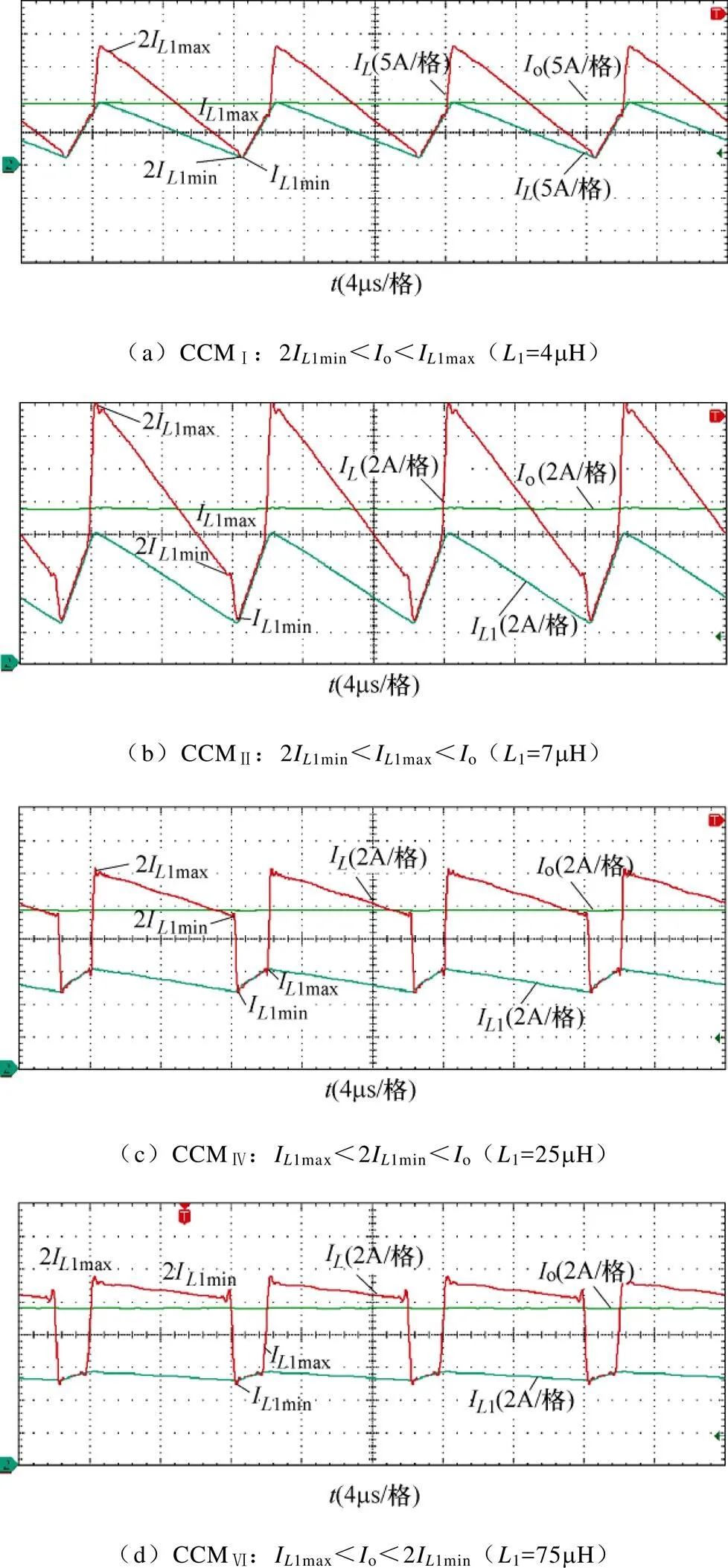
图14 不同电流关系下的相应电流波形（开环CCM）

仍采用表2所示参数，而使电感1取值分别满足=30%（1=25mH/CCMⅣ）、=10%（1=75mH/ CCMⅥ）和=1%（1=750mH/CCMⅥ），并令占空比变化D=0.155，得到开环下开关电感单元电流I、负载电流o及输出电压o的响应如图15所示。随电感的增大负调现象越明显，初值欠冲幅值越大，穿越时间越长，与图4和表3结论一致。同时由表3已知负调与开关频率无关，结合图15c进而可知SLBC应避免工作在极低开关频率下。

DCM下仍采用表2参数并仅改变电感1，则只会改变输出电压大小和动态响应快慢，不会有负调现象，且开关电感单元电流与负载电流仅存在一种关系，不同电感量下的时域响应（开环DCM）如图16所示，符合图6及第2.2节的理论分析。

CCM下若令电感电流纹波系数分别为50%、30%、10%，输出电压纹波系数均为1%，则对应感值、容值及工作区域分别为1=15mH/o=212mF/ CCMⅣ、1=25mH/o=178mF/CCMⅣ和1=75mH/o= 169mF/CCMⅥ，最终电容综合取200mF，则RHPZ频率及LC谐振极点频率对应分别为91.4kHz/3.7kHz、54.8kHz/2.9kHz、18.3kHz/1.6kHz。可知电感越小，RHPZ离极点频率越远，影响越小。

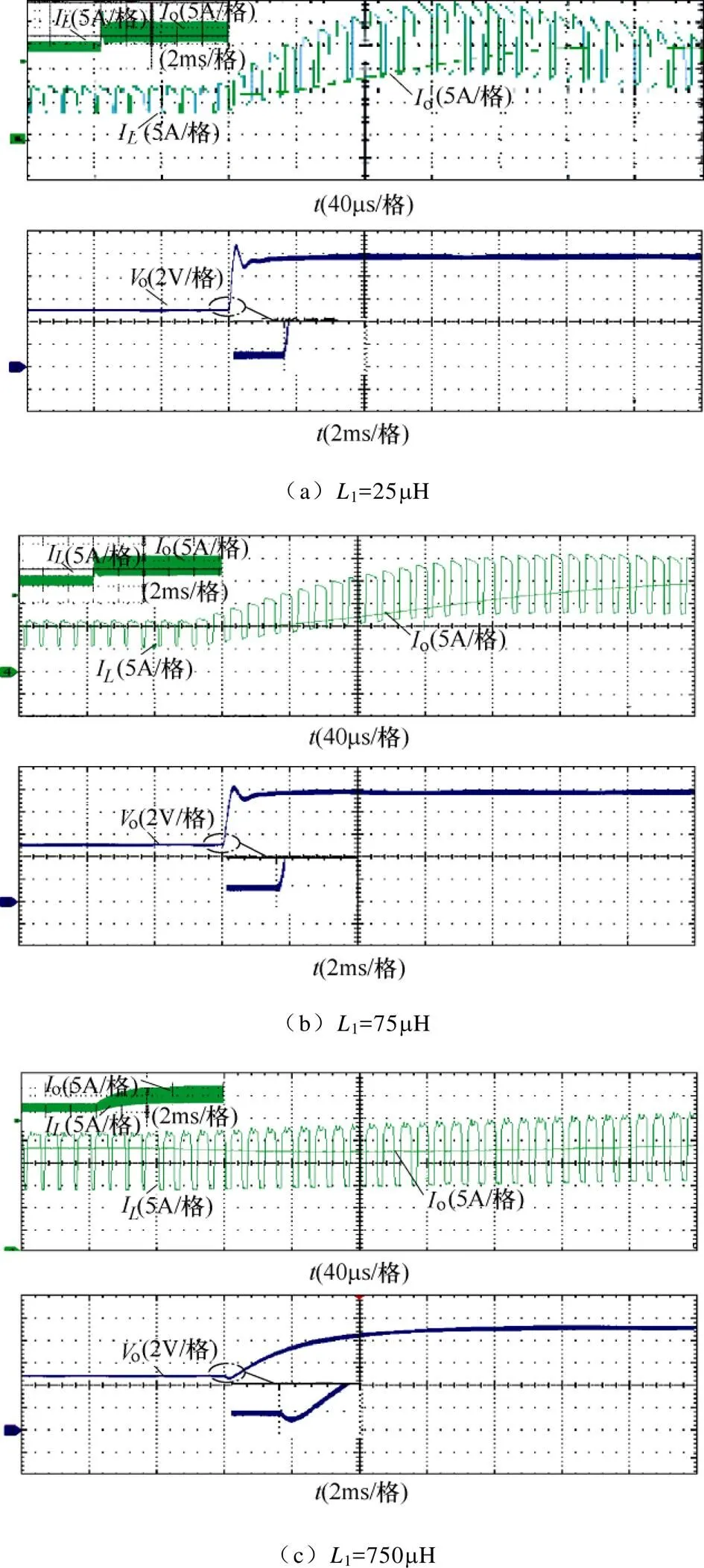
图15 不同电感量下的时域响应（开环CCM）

利用上述各组参数进行加减载切换（o=5A→ 10A→5A），并均使用电感电流内环单P控制（pi），输出电压外环PI控制（pv、iv），其中控制参数分别为pi=0.01、pv=2、iv=8 500,pi=0.04、pv=1.5、iv=6 000,pi=0.1、pv=0.8、iv=2 000。从图17可看出，1=25mH时仅需0.24ms就可恢复稳态，电压波动仅为0.8V。当电感减小到1=15mH时，仍可工作在CCMⅣ区域，但整体调节速度和电压波动已无较大提升，若继续减小使其工作在CCMⅡ区域时动态响应已无优化空间，而电感电流纹波会更大。当电感增大到1=75mH时，在CCMⅥ区域，调节时间增加到0.56ms，最大电压波动也达到了1.2V。综上CCMⅣ为最佳工作区域，符合第3节理论分析。

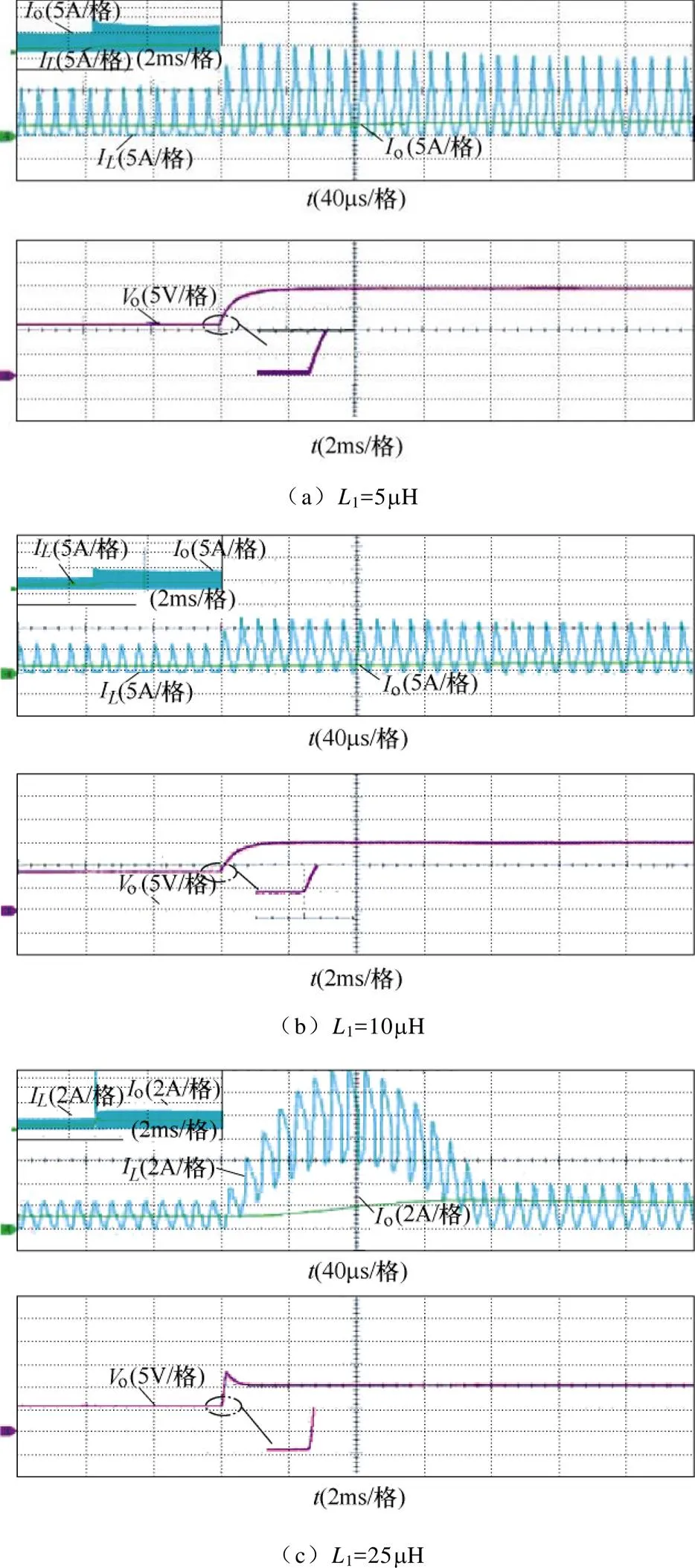
图16 不同电感量下的时域响应（开环DCM）

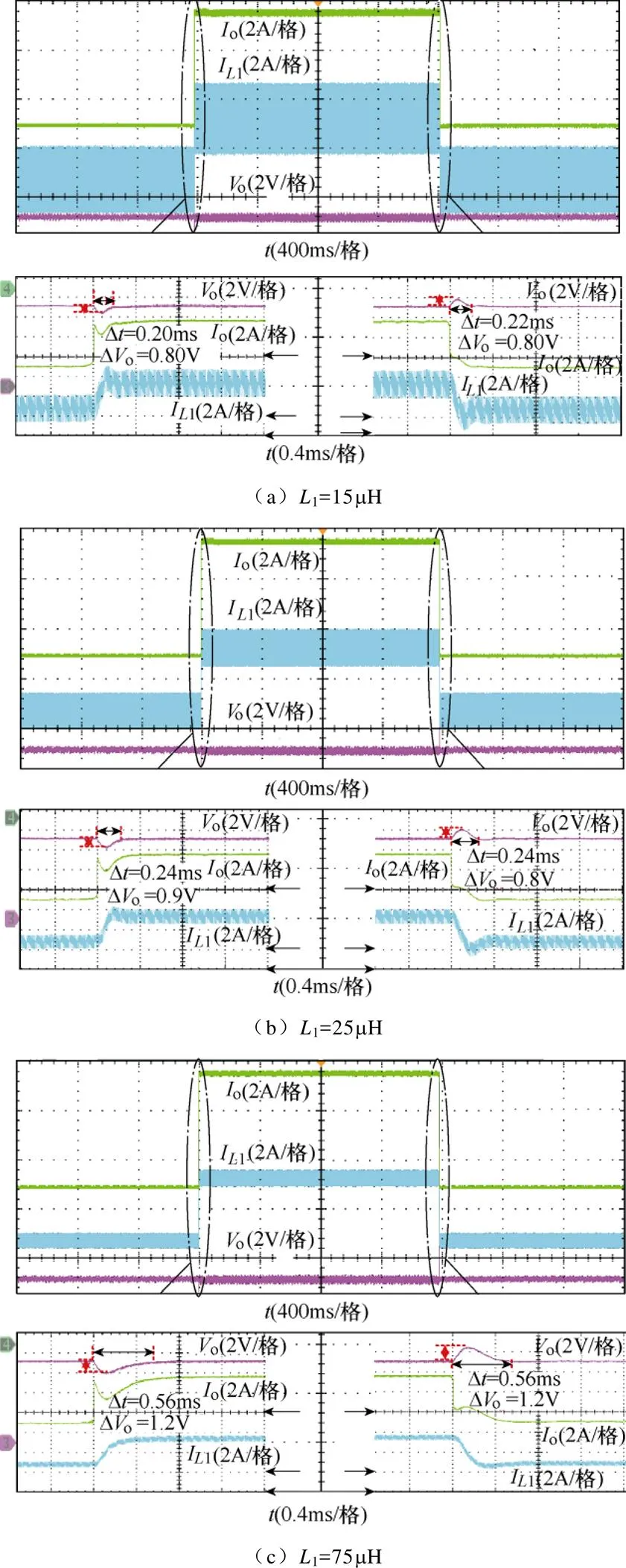
图17 不同电感量下的动态响应（闭环CCM）

5 结论

开关电感可使传统Buck变换器实现宽范围或高降压比变换，但开关电感的引入使参数设计和系统特性发生改变，本文以SLBC为例，对其进行了详细研究，得到以下相关结论：

1）CCM下开关电感单元电流与负载电流间共存在与电感和占空比相关的六种关系，可将CCM划分为CCMⅠ～CCMⅥ六个区域；DCM下仅存在负载电流永远小于电感电流最大值这一种关系。

2）CCM存在负调现象，根据建立的小信号模型揭示了SLBC因开关电感的引入，使之成为非最小相位系统，存在RHPZ，参数设计不恰当时会影响系统的稳定性和动态响应速度。

3）DCM下无负调现象，由提出的更简洁的全阶模型面积法推导相应小信号模型，指出因右平面零点向高频移动（已远大于开关频率），对系统动态响应和稳定性影响较小。

4）CCM下结合CCMⅠ～CCMⅥ六个工作区域和RHPZ相对位置，电感、电容的最佳选择应能使SLBC工作在CCMⅣ区域，这使得该变换器工作在宽范围或高降压比工况时不仅能满足纹波需求，也因无源器件容量小而有助于提高功率密度，且可提高动态响应速度。

通过实验对以上结论均进行了验证，本文的结论也可为其他基于开关电感的DC-DC变换器参数设计和控制策略提供参考。

附 录

式（27）对应系数k和x分别为

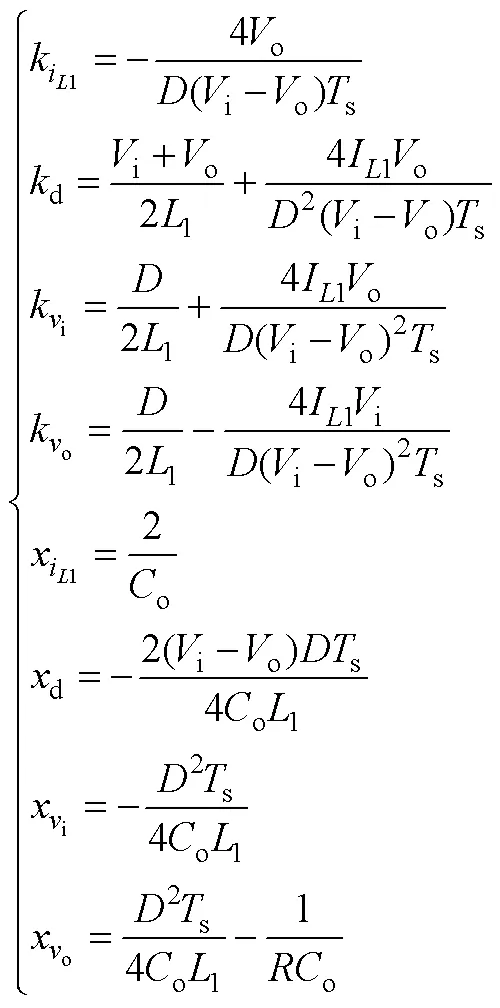
式（29）对应系数vd_D、vd_D及vd_D分别为

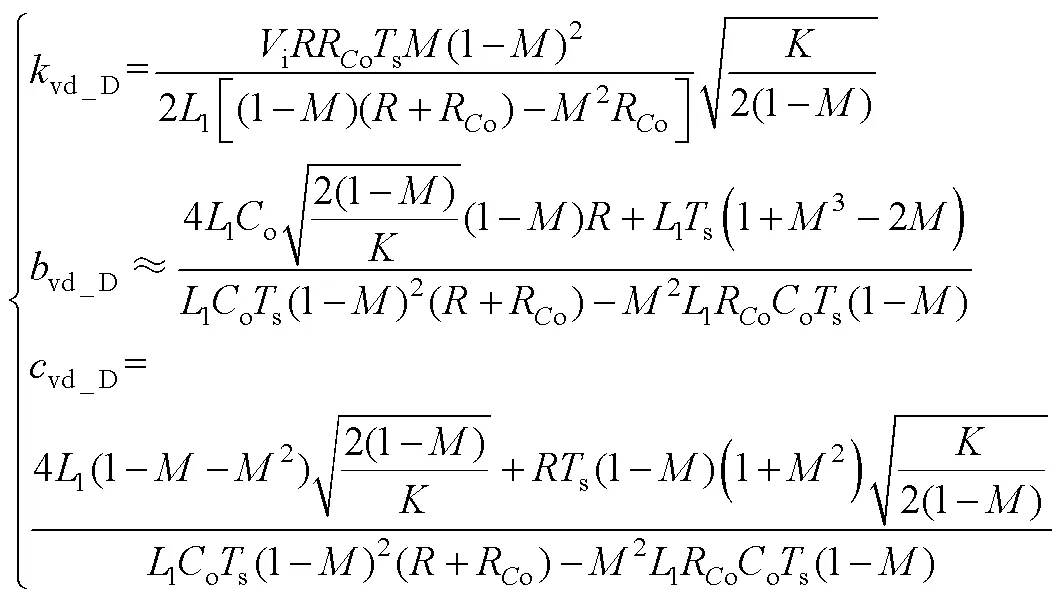
满足相同电压纹波需要的标幺化电容为

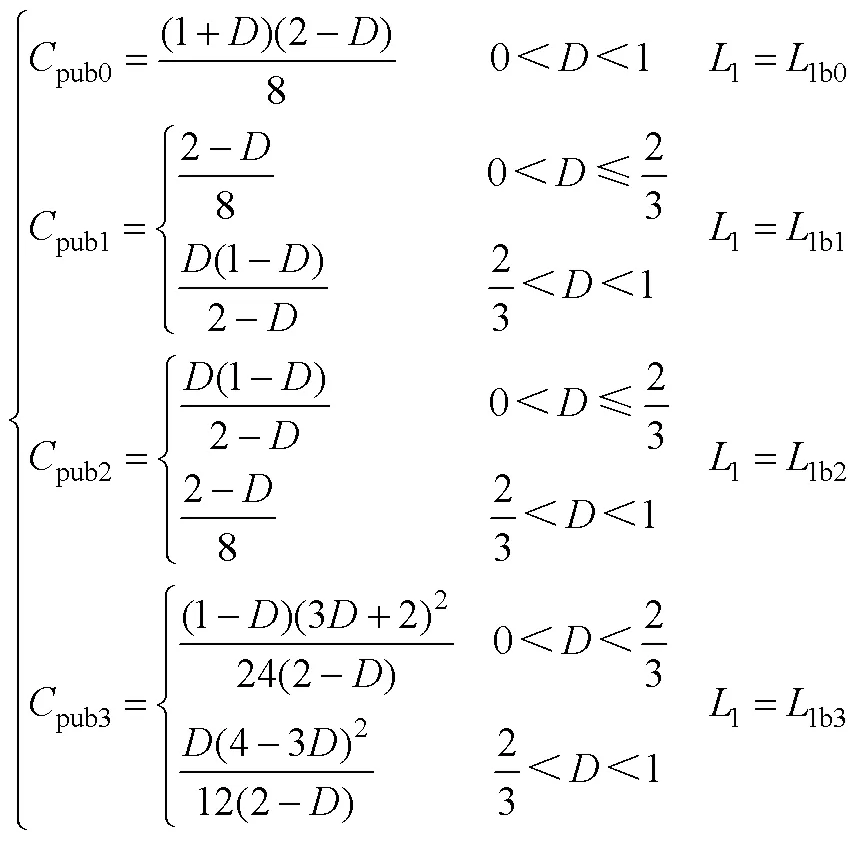
当1=1Z0=(2-)2s/(p)时

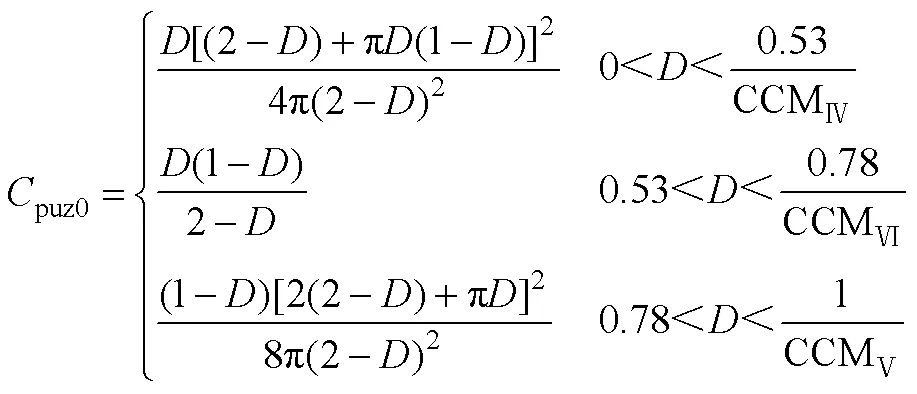
当1=1Z1=(2-)2s/(2p)时

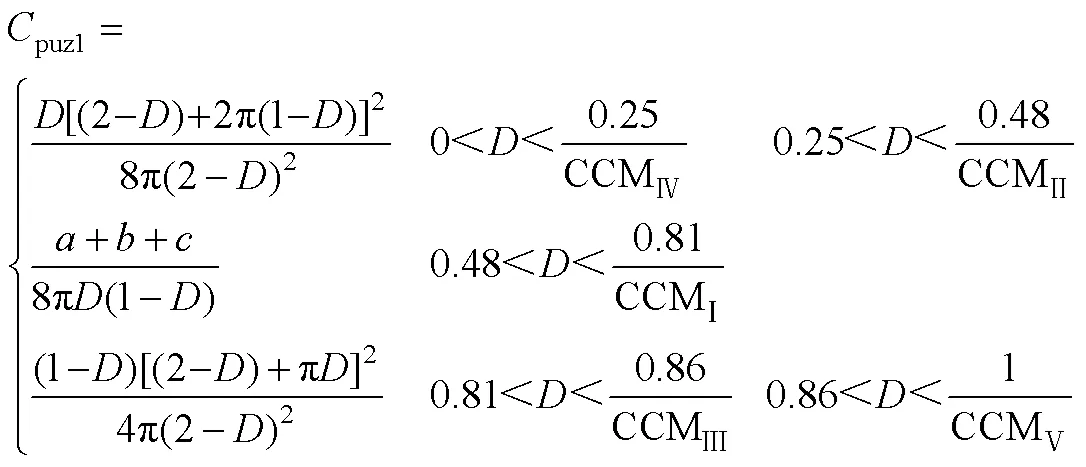
其中

[1] 丁杰, 高双, 赵世伟, 等. 基于耦合电感的对称式交错并联低输入电流纹波高增益DC-DC变换器[J].电工技术学报, 2021, 36(7): 1507-1515.

Ding Jie, Gao Shuang, Zhao Shiwei, et al. Symmetrical interleaved low input current ripple high step-up DC-DC converter based on coupled indu- ctor[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1507-1515.

[2] Yau Y T, Jiang Wenzhuang, Hwu K I. Ultrahigh step-down converter with wide input voltage range based on topology exchange[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5341-5364.

[3] 苏冰, 王玉斌, 王璠, 等. 基于耦合电感的多相交错并联双向DC-DC变换器及其均流控制[J]. 电工技术学报, 2020, 35(20): 4336-4349.

Su Bing, Wang Yubin, Wang Fan, et al. Multi-phase interleaved bidirectional DC-DC converter with coupled inductors and current sharing control strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4336-4349.

[4] 李洪珠, 刘飞扬, 刘艳, 等. 一种新型磁集成高增益耦合电感倍压Boost变换器[J]. 电工技术学报, 2020, 35(增刊2): 450-460.

Li Hongzhu, Liu Feiyang, Liu Yan, et al. A new magnetically integrated high gain coupled inductance voltage-doubled Boost converter[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 450- 460.

[5] Axelrod B, Berkovich Y, Ioinovici A. Switched- capacitor/switched-inductor structures for getting transformerless hybrid DC-DC PWM converters[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2008, 55(2): 687-696.

[6] Cornea O, Hulea D, Muntean N, et al. Step-down switched-inductor hybrid DC-DC converter for small power wind energy conversion systems with hybrid storage[J]. IEEE Access, 2020, 8: 136092 -136107.

[7] Arfin S, Mamun A A, Mahmood S N, et al. Ćuk derived SC-SL based high step down hybrid DC-DC converter[C]//2019 4th International Conference on Electrical Information and Communication Technology (EICT), Khulna, Bangladesh, 2019: 1-5.

[8] Rahman M A, Sakib S, Sarowar G, et al. A hybrid DC-DC Buck converter for very low voltage gain at high efficiency[C]//2017 IEEE Region 10 Humani- tarian Technology Conference (R10-HTC), Dhaka, Bangladesh, 2017: 710-713.

[9] Yang L, Chang E, Lin C. Study of a DC-DC converter with large step-down voltage conversion[C]//2013 International Symposium on Next-Generation Electro- nics, Kaohsiung, Taiwan, 2013: 465-468.

[10] 荣德生, 孙瑄瑨, 刘飞杨, 等. 一种新型磁集成二次型开关电感单元[J]. 电机与控制学报, 2020, 24(4): 131-140.

Rong Desheng, Sun Xuanjin, Liu Feiyang, et al. Integrated magnetic quadratic switched-inductor unit[J]. Electric Machines and Control, 2020, 24(4): 131-140.

[11] 杨惠, 晁凯悦, 孙向东, 等. 基于矢量作用时间的双向DC-DC变换器预测电流控制方法[J]. 电工技术学报, 2020, 35(增刊1): 70-80.

Yang Hui, Chao Kaiyue, Sun Xiangdong, et al. Predictive current control method for bidirectional DC-DC converter based on optimal operating time of vector[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 70-80.

[12] 苏善伟, 朱波, 向锦武, 等. 非线性非最小相位系统的控制研究综述[J]. 自动化学报, 2015, 41(1): 9-21.

Su Shanwei, Zhu Bo, Xiang Jinwu, et al. A survey on the control of nonlinear non-minimum phase systems[J]. Acta Automatica Sinica, 2015, 41(1): 9-21.

[13] Bose S, Hote Y V, Hanwate S D. Analysis of practical non-minimum phase systems by transfer function approach[C]//2018 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 2018: 500-505.

[14] 皇金锋, 李林鸿, 谢锋, 等. 含有右半平面零点的开关DC-DC变换器暂态性能分析及频域法设计[J].电工技术学报, 2020, 35(10): 2170-2180.

Huang Jinfeng, Li Linhong, Xie Feng, et al. Transient performance analysis and frequency domain design of switched DC-DC converters with right half plane zero[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2170-2180.

[15] Rana N, Kumar M, Ghosh A, et al. A novel interleaved tri-state boost converter with lower ripple and improved dynamic response[J]. IEEE Transa- ctions on Industrial Electronics, 2018, 65(7): 5456- 5465.

[16] Poorali B, Adib E. Right-half-plane zero elimination of boost converter using magnetic coupling with forward energy transfer[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8454-8462.

[17] Zhang Yan, Liu Jinjun, Dong Zhuo, et al. Dynamic performance improvement of diode-capacitor-based high step-up DC-DC converter through right-half- plane zero elimination[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 6532-6543.

[18] Sun Jian, Mitchell D M, Greue M F, et al. Averaged modeling of PWM converters operating in discon- tinuous conduction mode[J]. IEEE Transactions on Power Electronics, 2001,16(4): 482-492.

[19] Paduvalli V V, Taylor R J, Hunt L R, et al. Mitigation of positive zero effect on nonminimum phase boost DC-DC converters in CCM[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 4125-4134.

Characteristics Analysis of Buck Converter with Switched Inductor in CCM and DCM

11211

（1. National Active Distribution Network Technology Research Center Beijing Jiaotong University Beijing 100044 China 2. School of Automation Beijing Information Science and Technology University Beijing 100192 China）

Buck DC-DC converters with switched inductor can broaden the voltage conversion range and reduce the device current stress. However, in this paper, it is found that the series-parallel switching of the switched inductor unit will make the equivalent current equal to or twice the single inductor current, resulting in an uncertain relationship with the load current and making the converter a non-minimum phase system. Taking the switched inductor Buck converter (SLBC) as an example, based on the operation principle, it is pointed out that there are six matching relationships between the switched inductor unit current and the load current in the continuous conduction mode (CCM), which are closely related to the inductance & duty cycle and affect the output voltage ripple, and there is also a negative regulation phenomenon. In the discontinuous conduction mode (DCM), there is only one correspondence between the switched inductor unit current and the load current, and there is no negative regulation phenomenon. The small signal model of the SLBC is established using the conventional state-space averaging method and the full-order model area method in the CCM and the DCM respectively. It is shown that the RHPZ exists in this converter and the system characteristics are similar to a step-up DC-DC converter. Based on the six matching relationships and the relative position of the RHPZ, the best selection area of inductance and capacitance is given to meet the requirements of steady-state ripple and dynamic response comprehensively. Finally, the correctness of the analysis in this paper is verified by experiments.

Switched inductor, Buck, small signal modeling, right half plane zero, parameter design

10.19595/j.cnki.1000-6753.tces.211334

TM46

中央高校基本科研业务费专项资金资助项目（2020YJS168）。

2021-08-23

2021-10-13

祁静静 女，1998年生，博士研究生，研究方向为电力电子与电力传动。E-mail: 18117016@bjtu.edu.cn

吴学智 男，1975年生，副教授，博士生导师，研究方向为新能源并网技术、微网系统及大功率电机控制技术等。E-mail: xzhwu@bjtu.edu.cn（通信作者）

（编辑 陈 诚）