UG软件对电动冲击扳手冲击机构输出扭矩的仿真试验探索

曹友文

（ 南京久驰机电实业有限公司，江苏 南京 211102 ）

0 引言

冲击机构是电动冲击扳手等电动工具产品的关键部件。冲击机构将电机的旋转能量转换为冲击功。行星齿轮传动结构使得传递功率大、扭矩输出稳定，以此获得比电机本身扭矩大数十倍至上百倍的输出扭矩，从而达到拧紧螺栓的目的。本文以DC20 V电动冲击扳手为例，利用UG软件分析扳手的输出扭矩，通过实验验证分析结果的正确性。

1 结构

某款冲击扳手外形结构如图1所示，其冲击机构由主轴、压缩弹簧、冲击锤、钢球和输出轴等部件组成，主轴上有V型槽，冲击锤内壁V型槽与主轴V型槽相对应，钢球放置于两个V型槽之间的空隙内，在冲击锤内腔的压缩弹簧压力作用下，将主轴、冲击锤、钢球连接成整体。冲击锤的前端为输出轴，在拧紧或拆卸螺栓时，输出轴的四方头与套筒连接，两翼与冲击锤的凸台撞击，如图2所示。

图1 外形结构图

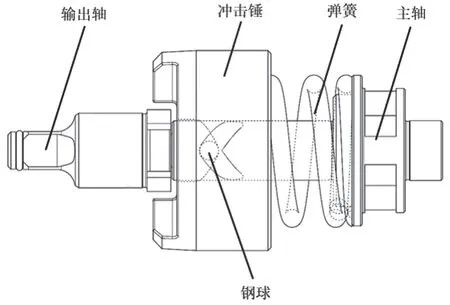
图2 冲击机构示意图

冲击机构的运动可分为小扭矩输出和大扭矩输出两个阶段。小扭矩输出对应螺栓拧紧的过程，大扭矩输出对应螺栓完全拧紧。

小扭矩输出时，螺栓仅受到较小的摩擦阻力。冲击机构中输出轴的两翼与冲击锤凸台始终保持接触状态，螺栓与冲击机构一同旋转。

大扭矩输出时，螺栓贴近紧固面，故无法继续向下旋转，同样与螺栓互相配合在一起的套筒和输出轴也无法转动。由于此时的电机仍处在工作状态，仍然通过主轴给整个系统提供动力，该动力使得钢球在主轴V型槽中滚动，滚动的钢球将力传递至冲击锤。此前，冲击锤凸台与输出轴两翼触碰，冲击锤受钢球传递的动力后，沿着接触面向后运动（图2冲击锤方向向右，弹簧压缩的方向），后退至一定距离，摆脱输出轴的束缚。

冲击锤后退过程中，弹簧被压缩，储存了大量的能量，当冲击锤脱离输出轴的束缚后，在弹簧弹力和钢球的作用下沿V槽螺旋上升（图2冲击锤方向向左，弹簧弹力释放的方向），等再次接触到输出轴的两翼时则以较高的角速度对其撞击，从而产生巨大的螺旋冲击力矩，螺栓也会受到输出轴的冲击力矩继续拧紧。之后冲击锤不断循环后退、上升、撞击的运动过程，使输出轴持续获得冲击力矩，最终可使螺栓完全拧紧。

冲击机构的小扭矩输出阶段是较为简单的运动过程，大扭矩输出阶段是相对复杂的过程，本文以DC20 V冲击扳手为例，利用UG软件，仅对扳手大扭矩输出阶段的输出扭矩进行分析探索，同时结合试验对分析结果验证，判断仿真分析的正确性。

2 运动分析

2.1 UG软件

软件具有较强的实体造型、曲面造型、虚拟装配、产品工程图等设计功能，在设计过程中可以进行有限元分析、机构运动分析，提高产品设计的可靠性。

2.2 3D模型

根据需要，建立DC20 V冲击扳手的UG 3D模型，提取需要分析的冲击机构部分，如图3所示。

图3 冲击机构的UG 3D装配模型图

进入UG软件的运动分析模块前，假定：

1）所有构件均为刚体，不考虑因构件的变形带来的影响；

2）主轴以恒定的转速运转；

3）忽略钢球在主轴V槽、冲击锤V槽之间形成的空间内滚动时的摩擦力；

4）压缩弹簧的弹性系数始终保持不变；5）假设与输出轴配合的套筒始终固定（模拟螺栓拧紧的状态）。

2.3 模型几何约束设定和数据采集

进入软件运动仿真模块对冲击机构的输出扭矩进行分析时，首先要根据实际的运动关系，建立冲击机构模型各个零件的运动副和运动约束。各零件的运动副设定见表1。由于冲击锤与主轴之间存在相对运动，两者的材料均为合金结构钢，且在实际运动过程中有润滑脂的作用，在设置时将摩擦系数设为0.08。

但如前所示，这一所谓的“天然”并不能从数学的函数观念中得出，而后者本应是弗雷格借由改造传统语义学的最重要凭据。在一个不显含自变量的数学表达式中，哪一部分被看作函数，哪一部分被看作自变量的值，完全取决于分析的方式。因此弗雷格的“概念-函数论”除了从数学中吸取养分外，一定还有其植根于前语言的理解，正是这一理解使得符号“Sokrates”只能成为专名。对弗雷格的这一理解有一个简单的解释：殊相是对象的模板，是最能被称为实体的东西。

表1 零件运动副

通过反复测试市面上应用较广泛的两款实测扭矩在1000N·m左右的DC20V冲击扳手，测得拧紧M24螺栓时的平均工作电流为51.3A和48.3A。两款扳手的测试电流值见图4。

图4 测试电流值

电机特性曲线如图5所示。选择电流值在50 A时的转速为电机工作转速，因扳手采用内齿圈固定的行星齿轮减速结构，根据公式，其中，Z内齿圈齿数为54，Z太阳轮,齿数为6，可得出传动比为10，故扳手冲击机构的主轴的工作转速约为1 200 r/min（计算不考虑实际工作时齿轮的传递效率）。

图5 电机特性曲线

3 动态仿真与样机测试

3.1 动态仿真结果

综上所述，对模型进行仿真求解计算，经过多次试验，设置仿真时间为1 s，仿真步长设为2 000步。待解算完成后，查看输出轴和套筒接触副的力的扭矩幅值，约为950 N·m。仿真扭矩图如图6所示。

图6 仿真扭矩图

其次，查看冲击锤的位移，图7所示。冲击锤与输出轴在每一次的撞击后，冲击锤的移动距离基本均等（不包含起始撞击的位移），理论上可判断每一次的撞击位置基本相同，不存在错乱撞击的现象。

图7 冲击锤位移图

3.2 样机测试结果

测试使用的SKIDMORE-WILHELM机械式螺栓夹紧力测试仪，如图8所示，其测量值为螺栓夹紧力，通过螺栓和夹紧力之间的换算关系计算出对应的扭矩值。

图8 机械式螺栓夹紧力测试仪

测试前用手拧紧螺帽，测试时扳手冲击3s左右并读取压力表数值，考虑人为误差因素，每台样机测试3次后取平均值为测试结果，样机测试时均使用满电电池。3台样机的测试数据见表2。

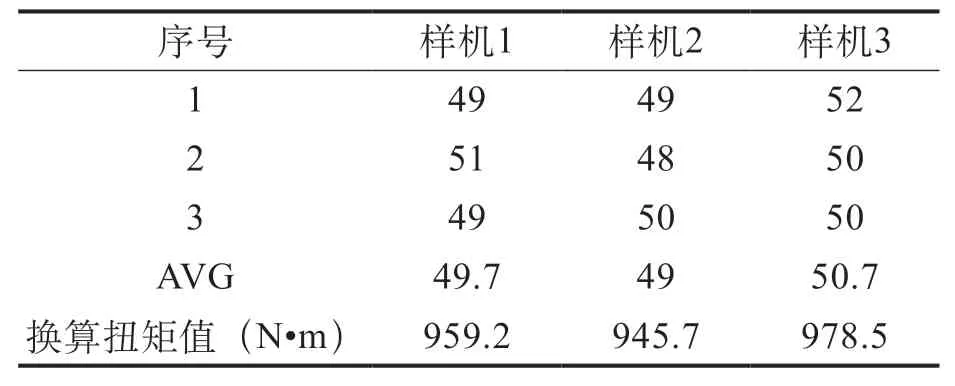
表2 样机测试数据

由表2测试数据可以看出实测扭矩值与仿真扭矩值较接近。为了验证扳手的冲击锤与输出轴撞击的完整工作过程，使用相机的快拍慢放功能对冲击锤的运动轨迹进行了采集。

拍摄前准备：在冲击锤凸台、输出轴两翼的侧面做好白色标识，便于拍摄观察；确保壳体的剖开区域能拍摄到冲击锤的工作状态，拍摄时长需大于一个完整的工作周期。

拍摄的冲击锤实际工作时的运动过程如图9所示。同时，使用示波器测试了样机在实打M24螺栓时的平均工作电流为50.1 A，测试电流值见图10。

图9 冲击锤实际工作的运动过程

图10 样机测试电流值

3.3 冲击锤单次冲击力

根据样机的测试数据和仿真试验结果，检验冲击锤的单次冲击力是否与测试结果接近。

检验前，假设：冲击锤每次撞击瞬间的角度速度相等；冲击锤每次撞击的力的大小、时间相等。

冲击锤角度速度如图11所示，读出撞击时冲击锤最大角度速度为16 500 deg/s。另外，在UG中查询冲击锤的参数：m=0.515kg，r=33.5×10-3m，J=57.8×10-5kg·m2， 从图11可知，冲击频率f=40次，冲击时间t≈0.0125s，根 据 公 式：，计算得出E≈24 J，而，计算得出F≈397.8 N。

图11 冲击锤角度速度

从表2中选取与仿真扭矩值接近的样机2的测试平均值49kN，假设每次冲击力相等的情况下，测试时冲击时间为3s，计算出平均每次冲击力为408.3N，与冲击锤的单次冲击力的计算值较接近。

4 结语

本文以DC20 V冲击扳手为例，利用UG软件仅对冲击机构其中的一种组合进行了简单的分析探索，也验证了UG软件对冲击扳手扭矩分析的可行性。后续的工作中可根据不同的设计需求，通过调整转速或冲击锤的重量、弹簧的弹性系数等参数，进行不同组合的仿真分析，对冲击扳手输出扭矩的合理性进行初步判定，确认该类产品的调整方向，减少不必要的样品制作时间，缩短整机开发周期。