改进的极小极大概率终端学习机
2022-08-22李晓萌代永潇范丽亚
李晓萌代永潇范丽亚
(聊城大学 数学科学学院,山东 聊城 252059)
0 引言
近年来,由Huang等人[1,2]提出的终端学习机(Extreme Learning Machine,ELM)受到学者们的广泛关注并不断加以改进。2017 年,受孪生支持向量机(Twin Support Vector Machine,TSVM)[3]的启发,Wan等人[4]提出了优化约束较少分类性能较好的孪生ELM(Twin Extreme Learning Machine,TELM)。2020年,Yang等人[5]提出了正则化ELM 套袋模型用于南海热带气旋轨道预测。2021年,Yang等人[6]提出了用于网络钓鱼检测的非逆矩阵在线序列ELM,该算法避免了矩阵的反演操作,并引入了在线序列ELM 的思想来更新训练模型。同年,Li等人[7]提出了混合数据径向基函数ELM 算法,实现了对混合数据直接、快速、有效的分类,Ouyang[8]提出了基于ELM 的改进自动编码器结构,通过利用低秩矩阵分解来学习最优低秩特征,Subudhi等人[9]提出了利用ELM 结合优化技术对电力功率质量自动分类。
针对数据分类,极大极小概率机(Minimax Probability Machine,MPM)[10]是指将最大错分率的概率最小化,是利用样本的均值和方差来寻找分类超曲(平)面。MPM 模型常被表述为一个二阶锥规划(SOCPs),通过内点算法进行求解,如SeDu Mi[11]。近年来,MPM 得到了广泛的应用,2014年,Yoshiyama等人[12]提出了拉普拉斯MPM(Laplacian MPM),将MPM 拓展到了半监督问题。2019年,Maldonado等人[13]提出了正则化MPM(Regularized MPM),降低了获得不稳定估计量的风险,提高了算法的泛化能力。2020年,He等人[14]提出了基于加权增量MPM 的汽油混合过程质量预测方法,Song等人[15]利用最小误差MPM 提出了新的奇偶校验空间故障隔离方法,Maldonado等人[16]提出了利用MPM 预测利润流失的方法,该方法最大限度地提高目标函数中的保留活动的利润。
2019年,Yang等人[17]将ELM 与MPM 结合,提出了极小极大概率终端学习机(Minimax Probability Extreme Learning Machine,MPME)框架用于模式识别,2020 年又提出了孪生MPM(Twin MPM,TWMPM)[18]用于模式分类。同年,Ma等人[19]也提出了孪生极小极大概率分类机(Twin Minimax Probability Machine Classification,TMPMC)。2020 年,Ma等人[20]还提出了孪生极小极大概率终端学习机(Twin Minimax Probability Extreme Learning Machine,TMPELM)用于模式识别。
由于在求解二阶锥规划问题的内点算法中,初始点要受到严格可行的限制,而在实际的问题中有时候难以找到严格可行点。本文在文献[10,13,17,20]的基础上,改进了MPM,MPME和TMPELM 算法的理论推导方法,将算法模型从二阶锥规划转化为凸二次规划,避免了初始点严格可行的限制,提出了改进的TMPELM,MPM 和MPELM 算法,并进行了对比实验。本文针对线性不可分数据集Rd×{±1},其中正类样本m1个,负类样本m2个,且m =m1+m2。用I1={i∈{1,…,m}:y i =1} 和I2={i∈{1,…,m}:y i =-1} 分别表示正负类样本的下标集。利用核函数k:Rd ×Rd→R(H是其RKHS,φ:Rd→H是对应的特征映射)可将数据集T转化为映射数据集

1 预备知识
本节简要回顾非线性RELM 算法和非线性TELM 算法,详细内容见文献[2,4]。为表述方便,设l=dim(H)(即H=Rl),其中l为充分大的正整数。将特征映射φ(·)表示为φ(·)=(φ1(·),…,φl(·))T。其中φt(·):Rd→R,记φtk:R→R。
1.1 RELM 算法
取隐层神经元个数为l,并设βt∈R是第t个隐层神经元到输出层(只有1个神经元)的权向量。和y i分别表示样本x i的网络输出和真实输出。记,则XTβ∈Rm。考虑下面的二次规划模型
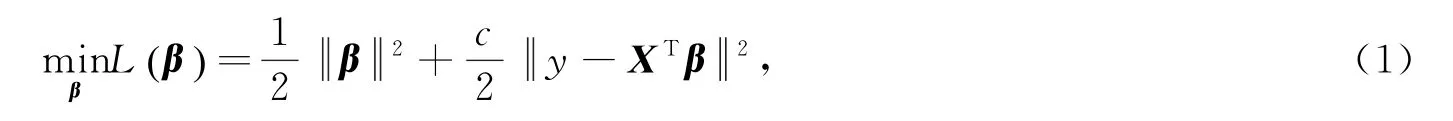
式中c>0为调节参数。由于H=span{φ(x1),…,φ(x m)}且β=[β1,…,βl]T∈Rl,故存在系数向量α∈Rm使得β=χα,于是,模型(1)可转化为
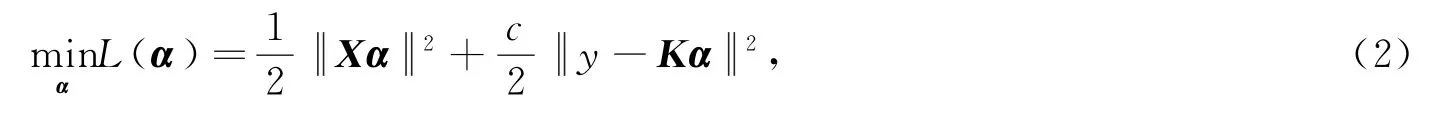
式中K =XTX∈Rm×m为核阵。令dF(α)/dα =0,可得
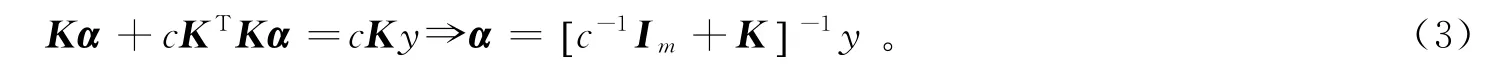
下面给出具体算法。
算法1(RELM)
步2 选择适当的核函数和核参数;
步3 利用(3)式,计算系数向量α*;
步4 对任一输入样本∈Rd,其RELM 输出为*∈R,其中x m)]。
1.2 TELM 算法
设输出层有2个神经元,一个是正类神经元,一个是负类神经元,并设β1t,β2t∈R分别是第t个隐层神经元到正类神经元和负类神经元的权向量。TELM 是通过考虑下面两个二次规划模型

来寻找一对非线性超曲面f1(x)=h(x)Tβ1=0和f2(x)=h(x)Tβ2=0,使得一个超曲面距离一类样本尽可能近,同时排斥另一类样本尽可能远,其中c1,c2>0是模型参数,h(x)是隐层神经元的输出向量。
记β1=[β11,…,β1l]T,β2=[β21,…,β2l]T∈Rl,则存在系 数向量θ1=(θ11,…,θ1m)T,θ2=(θ21,…,θ2m)T∈Rm,使得β1=Xθ1,β2=Xθ2,其中K x =[k(x,x1),…,k(x,x m)]∈R1×m,于是,模型(4)和(5)可分别转化为
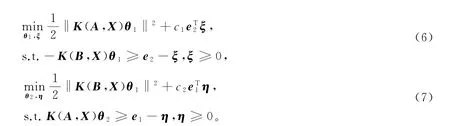
考虑模型(6)和(7)的Lagrange函数

并令∂L1/∂θ1=∂L1/∂ξ =0和∂L2/∂θ2=∂L2/∂η =0,可得

于是,模型(6)和(7)的Wolfe对偶形式分别为
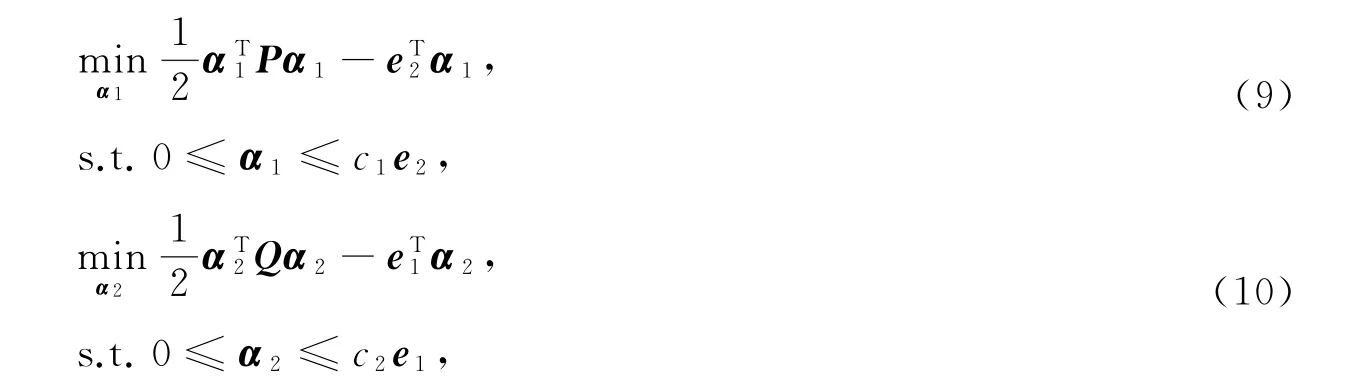
式中P=K(B,X)[K(A,X)TK(A,X)]-1K(B,X)T,Q=K(A,X)[K(B,X)TK(B,X)]-1K(A,X)T,α1∈Rm2,α2∈Rm1为Lagrange乘子向量。下面给出具体算法。
算法2(TELM)
步1 给定数据集T ={(x i,y i)}mi=1∈Rd×{±1},选择合适的模型参数c1,c2>0和正则化参数;
步2 择适当的核函数和核参数;
步3 分别求解对偶模型(9)和(10),得最优解α*1∈Rm2,α*2∈Rm1;
步4 利用(8)式计算系数向量θ*1,θ*2,其中α1=α*1,α2=α*2;
步5 构造分类决策函数f1(x)=K xθ*1和f2(x)=K xθ*2;
步6 对任一输入样本~x∈Rd,其类标签可判断为
2 极小极大概率机(MPM)
本节利用凸二次规划的Wolfe形式对原始MPM 算法进行改进,并提出新的MPM 算法。
设φ(x+)~(μ1,Σ1)∈Rl,φ(x-)~(μ2,Σ2)∈Rl是两个随机向量,其样本取值分别为φ(x+)∈Rl和φ(x-)∈Rl。记


来寻找分类超曲面f(x)=wTφ(x)+b=0,使得两个随机向量的样本取值分列超曲面两侧的最小概率(用概率的下确界表示)越大越好,其中w∈Rl,b∈R,α∈(0,1)。
引理1[21]设x ~(μ,Σx)是随机向量。给定w∈Rd{0},b∈R和α∈(0,1)使得wTμ≤b,则

推论1[21]设x ~(μ,Σx)是随机向量。若存在w∈Rd{0},b∈R和α∈[0,1)使得wTμ +b≥0,则,其中k(α)= α/(1-α)>0。
由引理1和推论1,模型(11)可转化为
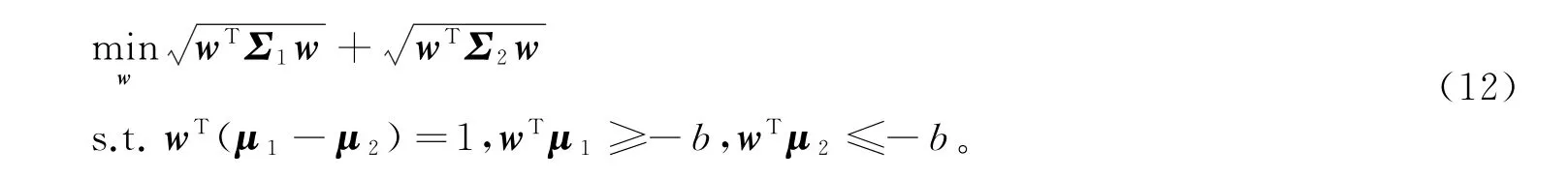
模型(12)可用SeDu Mi算法进行求解,详细内容见[10]。本文提供另一种思路和新的算法。
首先,将模型(12)等价地转化为
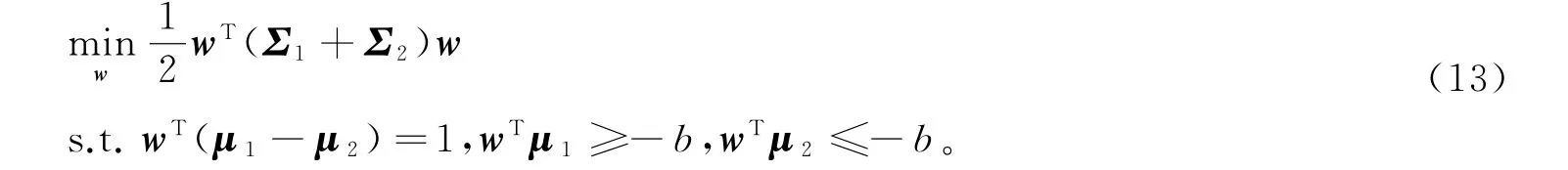
由于w∈Rl,故存在系数向量β=[β1,…,βm]T∈Rm使得w =Xβ。记
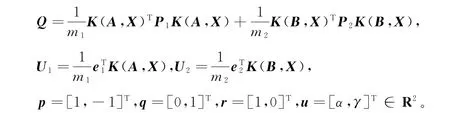
则分类超曲面和模型(13)可分别转化为f(x)=K xβ+b=0和

式中K x =[k(x,x1),…,k(x,x m)]∈R1×m。考虑模型(14)的Lagrange函数
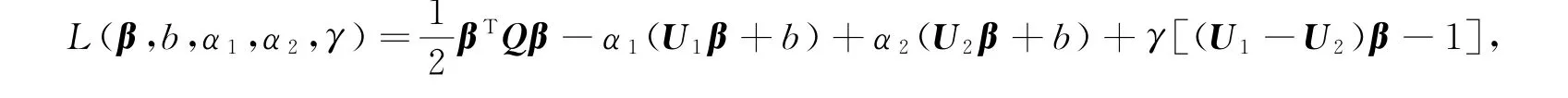
并令∂L/∂β=∂L/∂b=0,可得Qβ+(U1-U2)T(α-γ)T=0,其中,α=α1=α2。不妨设矩阵Q非奇异(否则,将其正则化),则有

根据模型(14)的约束,可取

于是,模型(14)的Wolfe对偶形式为

下面给出具体算法。
算法3(MPM)
步1 给定数据集T ={(x i,y i)}im=1∈Rd×{±1} ,选择合适的正则化参数t>0;
步2 选择适当的核函数和核参数;
步3 计算均值向量(μ1,μ2)和协方差矩阵(Σ1,Σ2);
步4 求解模型(17),得最优解u*∈R;
步5 分别利用(15)式和(16)式计算系数向量β*∈Rm和阈值b*∈R,其中u=u*;
步6 构造分类决策函数f(x)=K xβ*+b*;
步7 对任一输入样本∈Rd,其类标签可判断为
3 极小极大概率终端学习机(MPLEM)

类似于第2节,本节利用凸二次规划的Wolfe形式对原始MPLEM 算法进行改进,并提出新的MPLEM 算法。本文缩写符号均同第2节。不同于MPM,原始MPLEM 算法是通过下面的优化模型来寻找分类超曲面f(x)=wTX=0使得两类样本分列其两侧的最小概率越大越好,且真实输出与网络输出的误差越小越好,其中X=[φ1(x),…,φl(x)]T∈Rl,α∈(0,1),c>0是模型参数。由引理1和推论1,模型(18)可转化为

模型(19)可用SeDu Mi算法进行求解,详细内容见[15]。本文提供另一种思路和新的算法。
首先,将模型(19)等价地转化为

式中y=Xw为网络输出。由于w∈Rl,故存在系数向量β=[β1,…,βm]T∈Rm使得w=Xβ。则分类超曲面和模型(20)可分别转化为f(x)=K xβ=0和

式中K x =[k(x,x1),…,k(x,x m)]∈R1×m。记
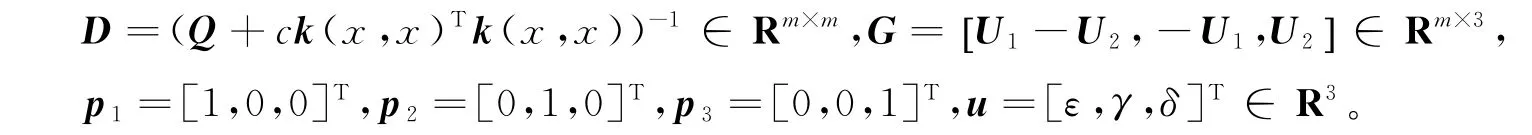
考虑模型(21)的Lagrange函数

令∂L/∂β=0,可得

通过求解模型(21)的Wolfe对偶模型
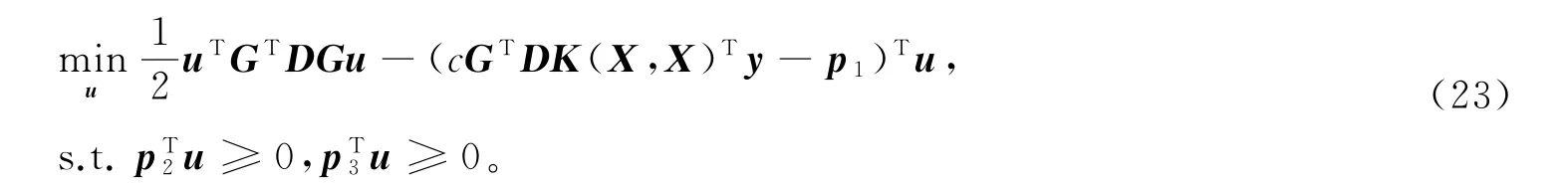
可得最优解u*,代入(22)式可得β*,下面给出具体算法。
算法4(MPELM)
步1 给定数据集T ={(x i,y i)}im=1∈Rd×{±1},选择合适的正则化参数t>0;
步2 选择适当的核函数和核参数;
步3 计算均值向量(μ1,μ2)和协方差矩阵(Σ1,Σ2);
步4 求解模型(23),得最优解u*∈R3;
步5 利用(22)式计算系数向量β*,其中u=u*;
步6 构造分类决策函数f(x)=K xβ*;
步7 对任意一输入样本∈Rd,其类标签可判断为
4 孪生极小极大概率终端学习机(TMPELM)
本节在第3节的基础上进一步改进原始TMPLEM 算法,并提出新的TMPLEM 算法。
原始TMPELM 算法是通过如下优化模型


来寻找正类超曲面f1(x)=wT1φ(x)=0和负类超曲面f2(x)=wT2φ(x)=0,其中w1,w2∈Rl表示超曲面的法向量,c1,c2>0是模型参数,使得正类(负类)样本位于正类(负类)超平面之上(下)的最小概率越大越好,同时排斥负类(正类)样本越远越好。同第2节相似,类似于第3节,模型(24)和模型(25)可用Se-Du Mi算法进行求解。详细内容见[20]。本文提供另一种思路和新的算法。

根据引理1和推论1,可将模型(26)和模型(27)分别转化为

其次,采用第3节的方法,将模型(28)和模型(29)转化为凸二次规划模型
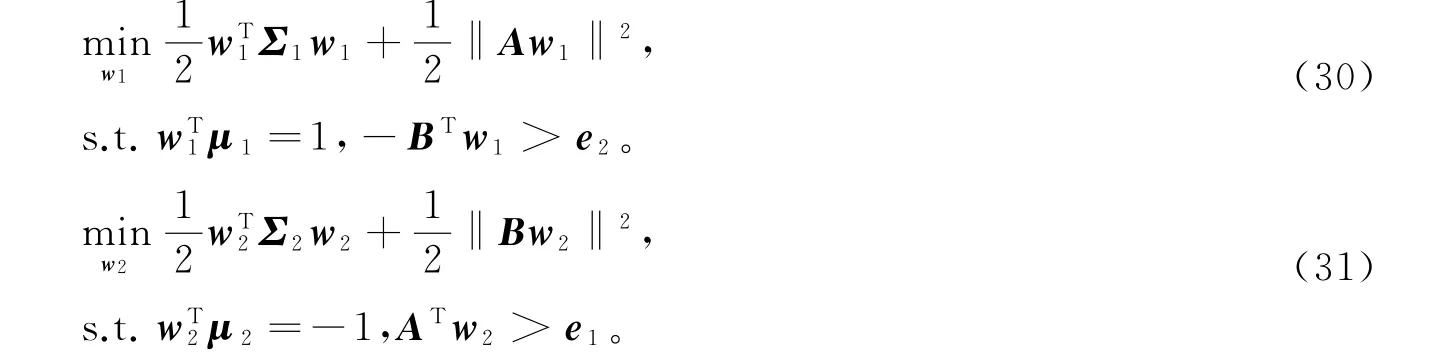
由于w1,w2∈H,存在系数向量θ1=[θ11,…,θ1m]T,θ2=[θ21,…,θ2m]T∈Rm使得w1=φ(X)θ1,w2=φ(X)θ2。于是,分类超曲面,模型(30)和模型(31)可分别转化为f1(x)=K xθ1=0,f2(x)=K xθ2=0和
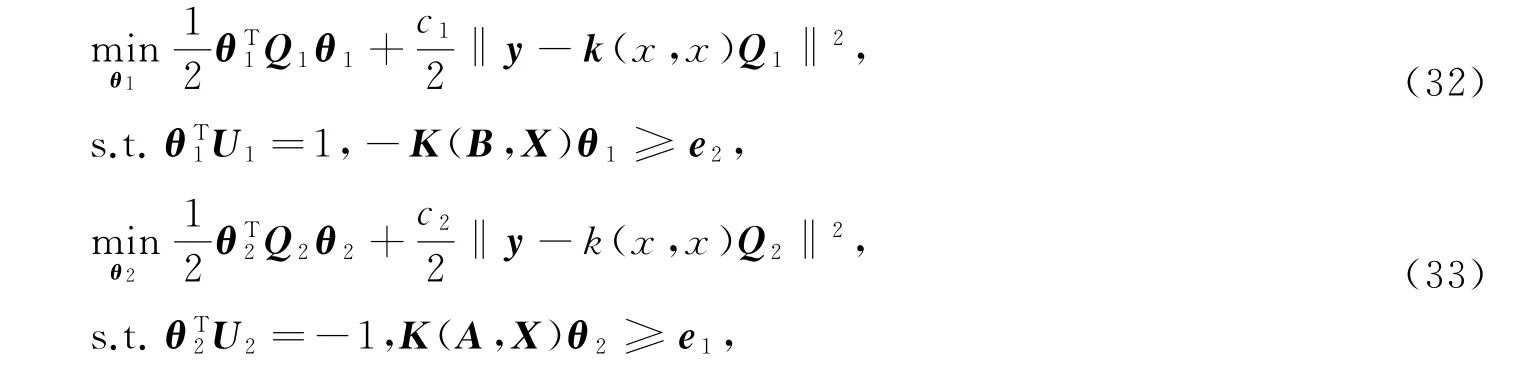
式中K x =[k(x,x1),…,k(x,x m)]∈R1×m,Q1=m-11K(A,X)TP1K(A,X),Q2=m-12K(B,X)TP2K(B,X)。记

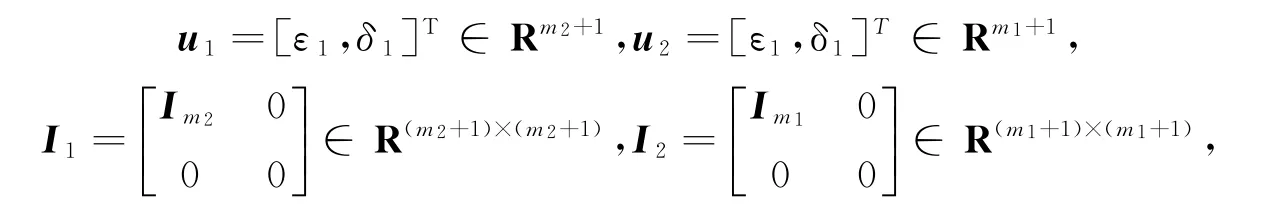
式中,I m1∈Rm1×m1,I m2∈Rm2×m2为单位矩阵。分别考虑模型(32)和模型(33)的Lagrange函数
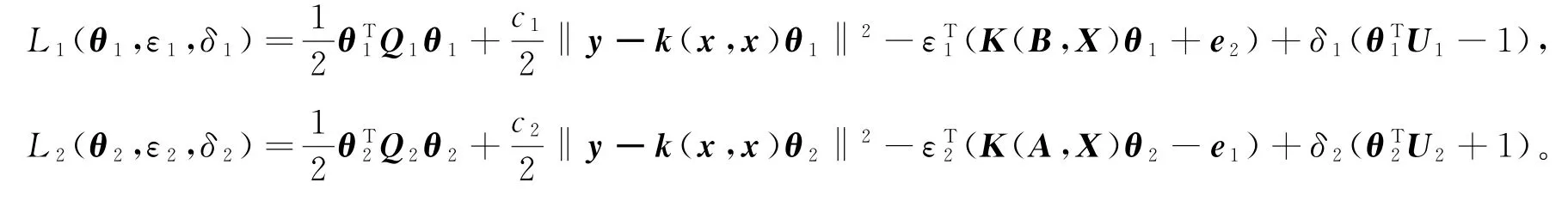
并分别令∂L1/∂θ1=0和∂L2/∂θ2=0可得

进而得模型(32)和模型(33)的Wolfe对偶形式

下面给出具体算法。
算法5(TMPELM)
步2 选择适当的核函数和核参数;
步3 计算均值向量(μ1,μ2),协方差矩阵(Σ1,Σ2)和矩阵G1,G2,D1,D2;
步4 求解模型(35)和模型(36),分别得最优解u*1∈Rm2+1,u*2∈Rm1+1;
步5 利用(34)式计算系数向量θ*1,θ*2,其中u1=u*1,u2=u*2;
步6 构造分类决策函数f1(x)=K xθ*1和f2(x)=K xθ*2;
步7 对任一输入样本~x∈Rd,其类标签可判断为
5 实验与结果分析
本节将文中提出的MPM 算法,MPELM 算法和TMPELM 算法分别与原始的MPM 算法[10,13],MPELM 算法[17]和TMPELM 算法[20]进行准确度、标准差和运行时间的对比实验。采用的部分数据集与运算开销同原始算法,使用十折交叉验证法并重复五次,分别取线性核和RBF核。所涉及的参数均使用网格搜索并取最优结果,搜索范围为10-3~103。实验结果分别见表1~3,其中ACC,S和T分别表示分类准确度,标准差和运行时间。为直观起见,同时提供了准确度对比柱状图。
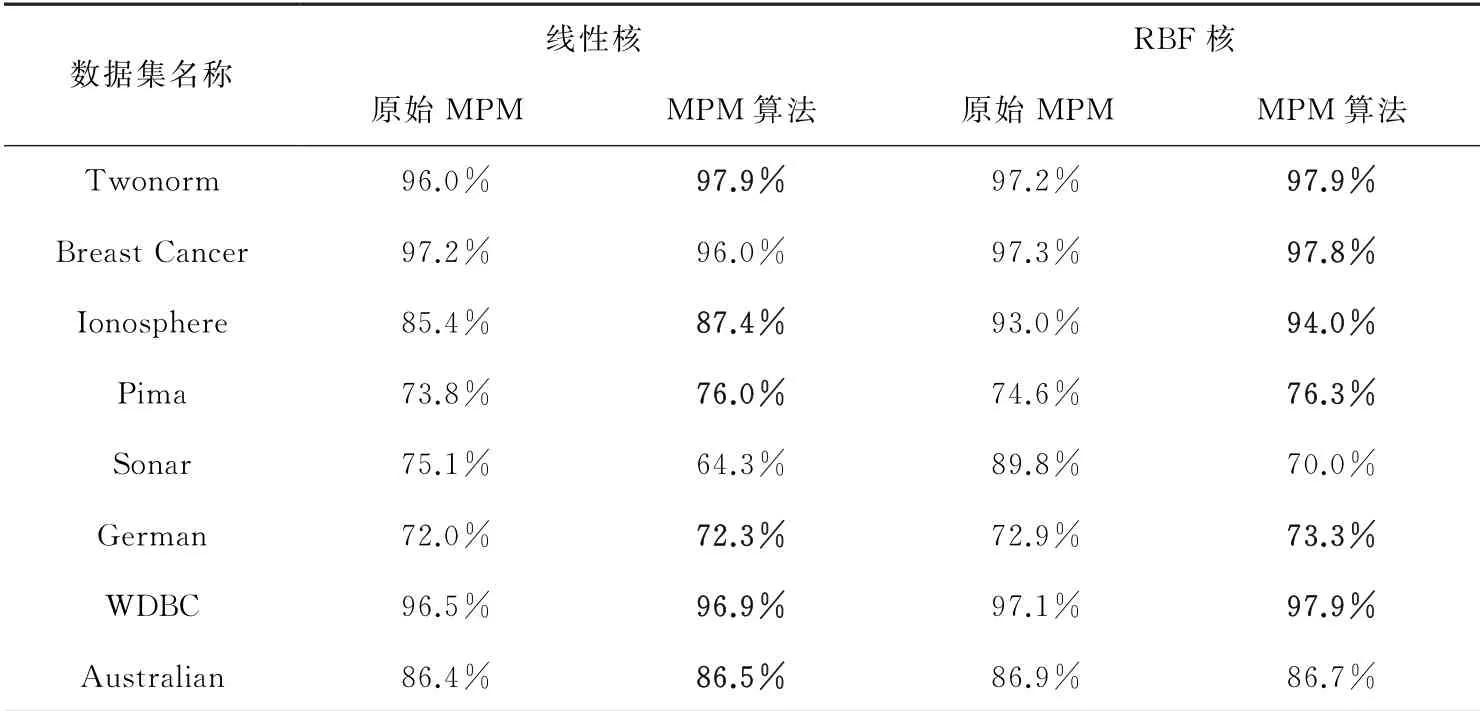
表1 MPM 算法准确度对比实验结果(原始MPM 算法只提供了准确度实验结果)

图1 MPM 算法准确度对比柱状图
从表1中可以看出,本文算法在线性核下有六个优于原始算法,在RBF核下有六个优于原始算法。
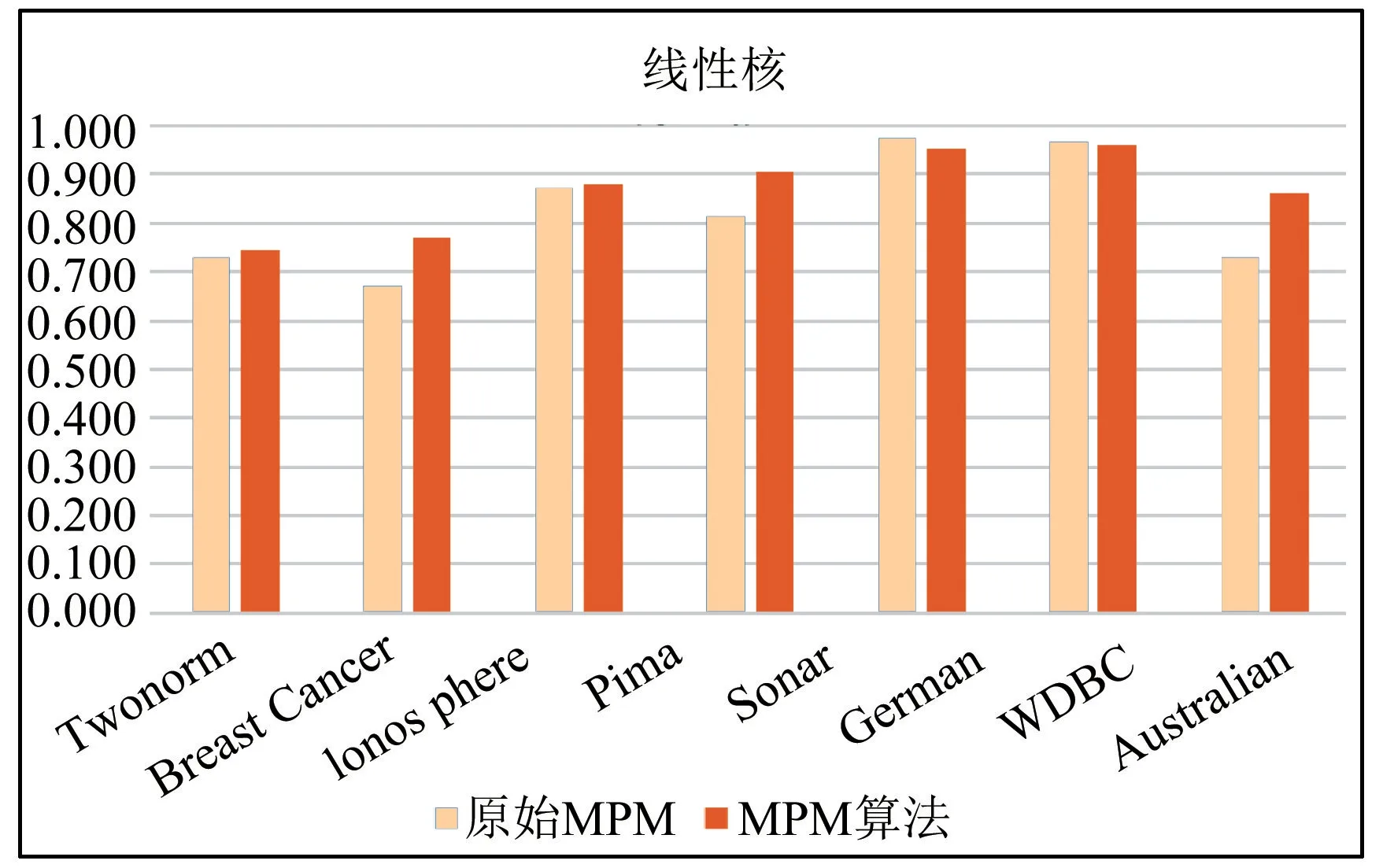
图2 MPELM 算法准确度对比柱状图
从表2中可以看出,本文算法有五个优于原始算法,尤其在数据集Pima,Spam 和Australian上准确度有显著提升,较原始算法分别提高了15.18%,11.59%和17.79%。
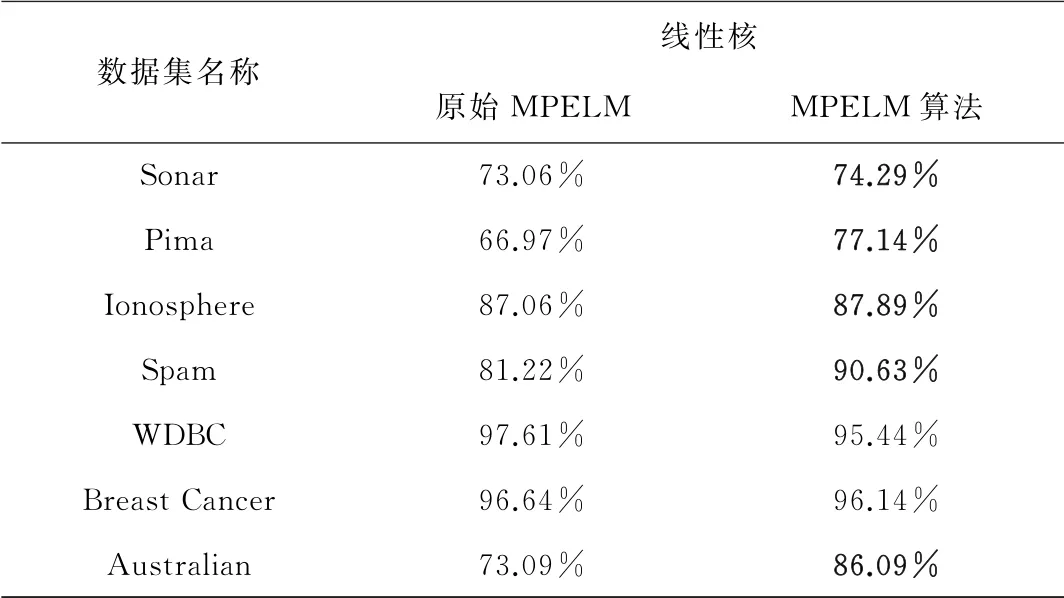
表2 MPELM 算法准确度对比实验结果(原始MPELM算法只提供了线性核下的准确度实验结果)

图3 TMPELM 算法准确度对比柱状图
从表3中可以看出,本文算法在线性核和RBF 核下均有七个优于原始算法,其中在数据集Banknote和Diabetes上准确度有显著提升,线性核下提升了11.25%和17.10%,RBF核下提升了9.87%和8.15%。综上所述,本文所提算法是有效的且具有可竞争性。

表3 TMPELM 算法准确度、标准差、运行时间对比实验结果
6 结论
针对二分类问题,MPELM 具有MPM 和ELM 的优点,但与之不同的是,MPELM 可以提供泛化误差的明确上界,这提供了一个分类精度的可靠性度量,且决策变量比MPM 和SVM 少。目前,MPM 算法,MPELM 算法和TMPELM 算法主要是通过求解二阶锥规划模型的内点算法实现,该算法初始点要受到严格可行的限制,在实际问题中有时难以找到严格可行点。本文利用支持向量机思想和凸二次规划的Wolfe对偶形式,对已有的MPM 算法,MPELM 算法和TMPELM 算法进行了改进,避免了寻找严格可行点,并提出了三个新算法。实验结果表明,本文所提算法是有效和可竞争的。在本文的基础上,可进一研究MPM 算法与其他形式的ELM 算法的有效结合,以期提高数据集的分类准确度,并将研究成果应用于信息的加密与解密领域。
