不平衡大数据阵列的挖掘算法仿真

邱 劲，张昭玉

(苏州科技大学电子与信息工程学院，江苏 苏州 215009)

1 引言

数据挖掘是在大量无规律的数据中挖掘有用信息数据的过程。在数据挖掘过程中，当其中某一个样本数据集的数据量与其他数据集的数据量相差较大时，则认为这个数据集中的数据为不平衡数据。不平衡数据通常维数较其他数据相比要高，样本数量过小，噪声较大，且冗余信息过多以及样本数据分布严重不平衡等，因此对其分析和挖掘难度较大。

目前，许多相关学者已经针对非平衡数据的挖掘问题展开研究。文献[1]提出利用多源数据融合算法实现不平衡数据的融合与挖掘。首先，在算法的聚类结果中引入综合评价指标法，以此来反映聚类结果的优劣性；其次，将多数类数据与少数类数据融合在一起，利用时空特征的位置来挖掘数据所处的位置区域，实现数据的有效挖掘。该算法相较于单源数据挖掘算法来说，具有更为理想的挖掘结果，但是该方法的只对不平衡数据进行了融合处理，导致结果含有较多的不确定因素；文献[2]利用SMOTERF法挖掘由数据不平衡流失的客户隐私信息。首先，对客户信息做平衡处理，引入分类预测方法提高AUC值，减少有效数据的流失；再通过SMOTERF法挖掘数据。该算法对于客户数据流失起到了很好的应对作用，但是对不平衡数据的平衡处理极易出现过度拟合情况，挖掘效果稳定性差。

本文在以上两项研究的基础上，针对已有方法存在的问题，提出了新的基于不平衡阵列判别的大数据集成挖掘方法。首先，针对不平衡数据的特点，采用过采样判定方式使其逐渐趋于平衡状态；通过提取所有不平衡数据的特征量，引入到语义动态分析模型中，实现数据挖掘的自适应寻优。

2 基于不平衡阵列判别的数据过采样处理

对于判别出的不平衡数据，本文通过采样处理使数据达到平衡。采样处理主要分为两种，分别是过采样处理以及欠采样处理[3]。过采样处理，通过在少数类样本中增加一些合理的伪样本，实现与其他类别的平衡；而欠采样处理则主要针对多数类样本，采用某种算法剔除掉包含的噪声和杂质，通过这种操作，来达到与少数类样本平衡的目的。综合比对之下，本文选择过采样处理来使不平衡数据达到平衡状态[4]。

在少数类中增加的伪样本，主要是通过复制正样本来实现的，这种方法具有较低的成本和计算复杂度。但是对于维数高、噪声高的不平衡数据来说，直接过采样处理可能会导致最终结果出现过度拟合的情况，因此，本文使用概率分布[5]判别不平衡阵列进行过采样处理，通过对数据集中每一个样本进行基因上概率分布计算判别，根据计算结果生成与之相对应的伪样本。这样即保证了生成伪样本的合理性，又保证了概率分布前后数据基因的一致性，使得最终生成的伪样本数据集更加合理。

对不平衡阵列中的所有数据进行基因均值和方差计算，获得数据在阵列中的正态分布情况。但是考虑到不平衡数据的特点，在数据样本数量过少情况下，最终结果会存在较多的不确定因素，含有较多的杂质和噪声。因此，本文通过非参数的概率密度估计法剔除噪声杂质。首先，对每个样本设定合理的取值范围，并对其进行离散化处理，划分该范围为若干个等宽但并不相交的区间。假设基因的取值范围在[1，2]之间，按照0.1的宽度进行离散化处理[6]，那么该基因的取值范围可以划分为[1，1.1)，[1.1，1.2)，……，[1.9，2]共十个区间。这十个区间在不平衡阵列中的概率分布情况如图1所示。

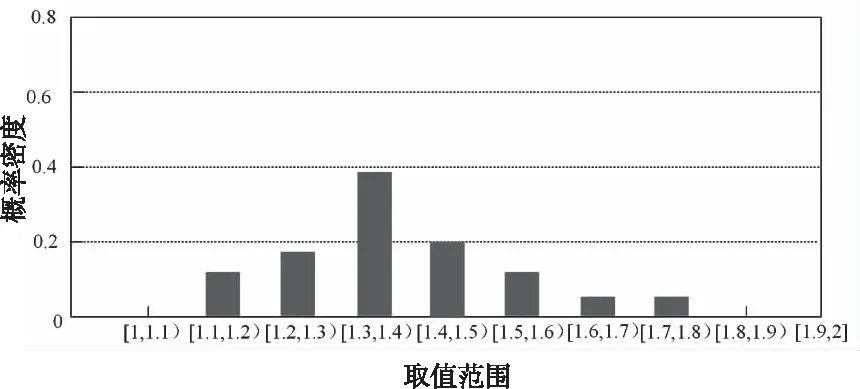
图1 样本数据概率分布评估结果

从图1中可以看出少数类数据集中样本概率的分布情况，本文生成的伪样本也服从这种分布。实现过程为：

1)随机生成一个(1，2)之间的数值；

2)根据图1中各个取值区间内概率的分布情况，计算随机数的取值区间；

3)从该取值区间内，随机选取一个数值作为伪样本在此基因上的表达值[7]。

综上所述，利用阵列判别方式生成的伪样本与原始样本概率分布情况一致，同时又存在一部分的随机性，在一定程度上提高了少数类数据集的质量，使不平衡阵列逐渐趋于平衡。

3 大数据集成挖掘的实现

3.1 大数据聚类分析

利用特征匹配方法实现大数据的模糊特征聚类[8]，并对完成过采样处理后的数据集自适应加权学习计算。大数据模糊特征聚类分布如式(1)所示

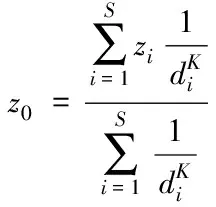
(1)

式中，z0表示不平衡阵列中大数据的关联估计值；zi表示在点i处采集到的大数据集的实测值；di表示点i与点0之间具体的距离值；S表示不平衡阵列中大数据实测点的统计特征量；K表示数据挖掘中的插值权重[9]值大小。

接下来对不平衡阵列进行大数据的自适应加权计算。构建大数据模糊加权学习式，以此来提高自适应挖掘能力。得到的空间聚类模型用式(2)表示为

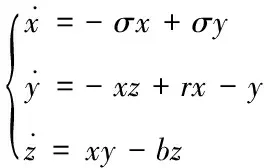
(2)

式中，x、y、z分别表示不平衡阵列中大数据在三维空间内的语义相似度特征量；σ表示大数据的语义本体集；b表示数据挖掘过程中产生的模糊度系数；r表示粗糙特征匹配集。

3.2 大数据特征提取

通过上文计算得到的大数据语义关联特征量，与模糊属性特征检测方法结合使用，实现对不平衡阵列大数据的统计检测[10]。利用统计分析方法进行语义分割，计算公式如下所示

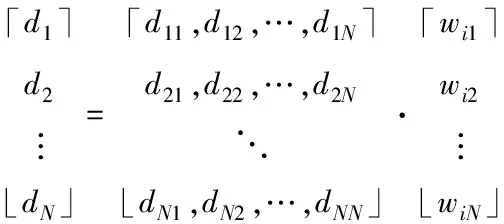
(3)

式中，wij表示点i在大数据集成挖掘中的全局加权值；dij表示数据集中各个样本数据分布节点的聚类中心；N表示大数据集成挖掘节点的维数。

在实现大数据的挖掘之前，要完成特征提取，本文通过构建特征提取模型来实现。在STARMA(1，1)网络模型中，可视化分割大数据，根据数据的输出结果构建自相关特征匹配模型，再引入模糊特征聚类分析方法，完成对大数据的分析与统计。再利用模糊信息对大数据进行特征提取，随机选取一个特征点i，计算其在t时刻下的特征分布集为(w1j，w2j，…wtj)，wtj代表的是t时刻下大数据集成挖掘加权系数值。结合语义特征分析方法，构建大数据模糊语义特征规则集，以此得到自适应加权系数为

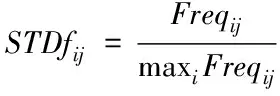
(4)

式中，Freqij表示大数据挖掘寻优的迷糊约束特征量。计算不平衡阵列的信息素浓度，如式(5)所示

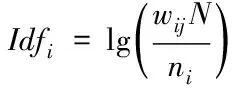
(5)

其中

wij=tfij

(6)

式中，ni表示第i个数据节点信息在挖掘过程中的嵌入维数；fij表示数据节点i与节点j之间的关联程度。

3.3 大数据集成挖掘输出

构建不平衡阵列的语义动态特征分析模型，提取每个样本数据的统计特征量，进行数据挖掘的自适应寻优，计算公式如式(7)所示

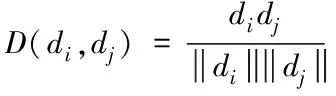
(7)

式中，di、dj分别表示大数据挖掘的模糊规则特征量。利用统计信息分析方法，构建模糊特征分布集，如式(8)所示

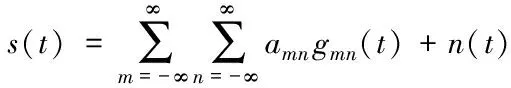
(8)

式中，m、n分别表示样本数据的嵌入维数和分割网格数；amn表示不平衡阵列中所有待挖掘数据的幅值大小；gmn(t)表示不平衡数据经过统计之后所得的平均值；n(t)表示挖掘过程中的干扰因素。综上所述，针对不平衡阵列中大数据集成挖掘模型为

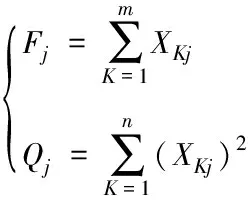
(9)

式中，XKj表示语义分割的关联维数，Fj表示大数据集成挖掘的输出特征量，Qj表示大数据集成挖掘的数据信息分量。

4 仿真研究

为验证本文方法对于不平衡数据挖掘是否合理有效，与引言中提到的多源数据融合算法和SMOTERF法展开对比仿真验证。在实验中，共选取了sonar(声纳)、vehicle(交通工具)、pendigits(数字)三组UCI数据作为数据集(机器学习标准测试数据集，是加州大学欧文分校提出的)，详细信息如表1所示。

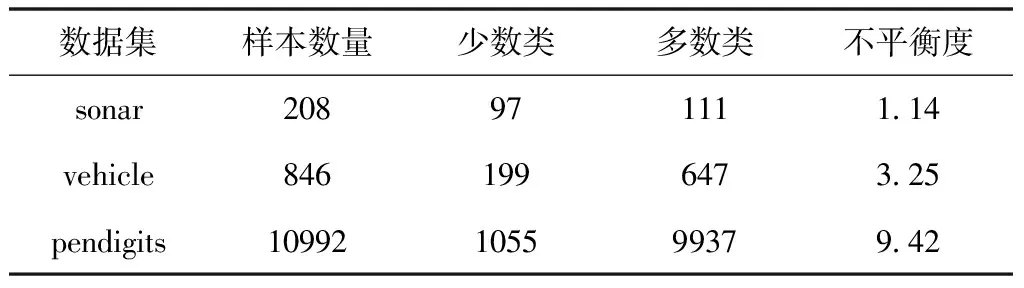
表1 三组UCI数据详细信息

一般情况下，会对不平衡度设定一个取值区间，以此来判定该数据集的不平衡度程度。在区间[1.5，3.5)内的为低度不平衡，[3.5，9.5)内的为中度不平衡，[9.5，+∞)内的为高度不平衡。表1中选取的三组数据集正是处于不同范围内，但是不难发现，sonar数据集并不在设定的取值范围内，所以该数据集也被称为平衡数据集，选取该数据集的目的是为了验证本文方法是否可以在处理平衡数据集时依然有效。

4.1 不平衡阵列判别处理后大数据集均衡效果

首先对本文方法的挖掘效果进行实验测试，实验在Matlab软件中进行，将不平衡阵列中数据采样的节点数设定为120，数据挖掘的根节点设定为12，数据特征聚类划分的类别数为10。数据初期采样频率设定为f1=1.5Hz，末期采样频率设定为f2=2.3Hz。

在上述实验环境下，通过不平衡阵列判别数据中的不均衡个体，去除大数据内噪声和异常信息，实验结果如图2、图3、图4所示。

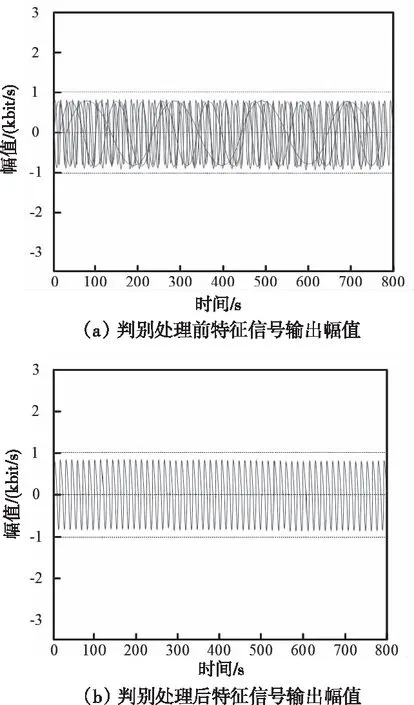
图2 sonar数据集不平衡阵列判别前后

从图2能够看出，处理前sonar数据集的特征信号输出幅值处于一定区间内，是平衡数据集，但是包含过多干扰信息，无法获得清晰有效特征。经不平衡阵列判别后剔除了大量无规则干扰，使数据集特征明显，方便后续集成挖掘处理。

从图3中可以看出，处理前vehicle数据集信号幅值变化没有规律，信号中含有较多的噪声和杂质，无法实现精准的特征识别。而经过不平衡阵列判别处理后，信号幅值呈现出明显的规律，并且消除了噪声和杂质的影响，为后续的数据集成挖掘做好了基础工作。

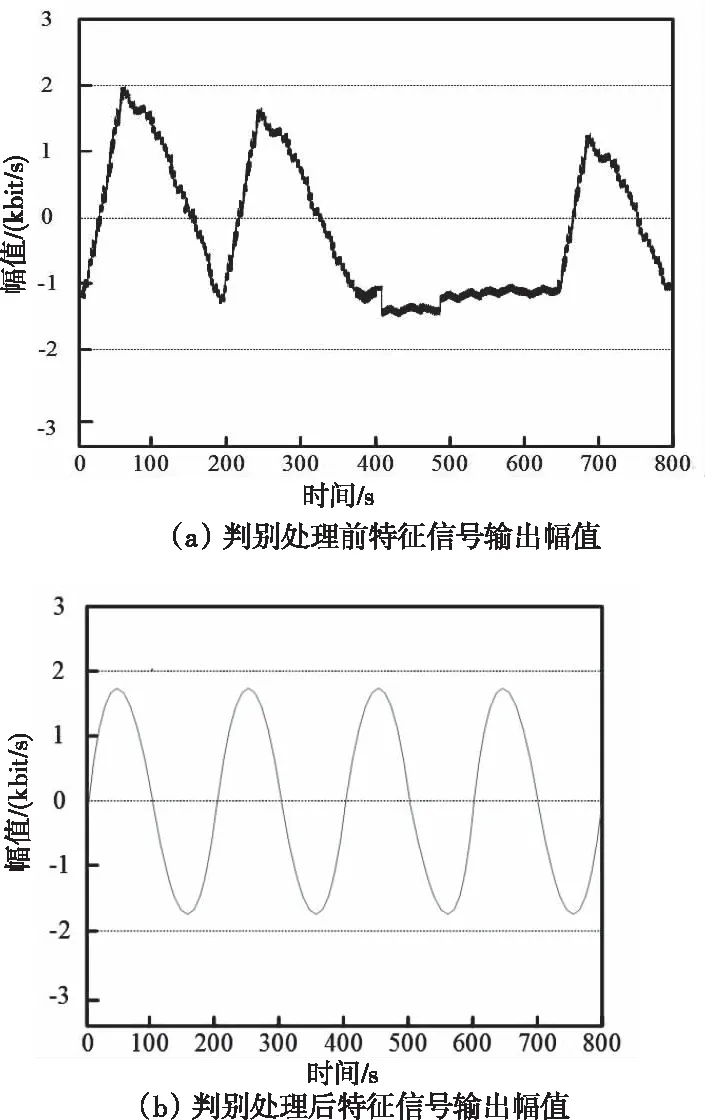
图3 vehicle数据集不平衡阵列判别前后

从图4中可以看出，pendigits数据集在没有处理之前，信号幅值变化幅度非常大，且没有规律可循，要对其进行数据挖掘几乎是不可能实现的。而经过处理后的特征信号开始趋于平衡，幅值的变化也具有一定的规律，有效抑制了不平衡数据的干扰影响，帮助后续精准挖掘挖掘实现有效预处理。

图4 pendigits数据集不平衡阵列判别前后

4.2 F-measure值和AUC值对比

4.2.1 评价指标

接下来对本文方法、多源数据融合算法以及SMOTERF法，在F-measure值和AUC(ROC曲线下方的面积大小)值方面展开对比测试。F-measure值是精确度和召回率的调和值，能够充分验证挖掘结果优劣，其计算结果接近于二者中数值较小的那一个，越高说明集成挖掘方法越有效，精确度和召回率的综合性能越大，可以充分反映出少数类的挖掘情况；而AUC值能够客观地描述不同阈值下的数据挖掘性能。

F-measure的计算公式为

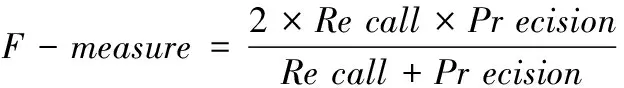
(10)

AUC的计算公式如式(11)所示，AUC的最终结果通常在[0.5，1]区间内波动，数值越大，说明算法的挖掘性能越理想。

(11)

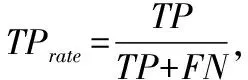
实验中，通过F-measure值和AUC值作为算法挖掘性能的评价指标。

4.2.2 评价结果

根据以上两个评价指标进行实验对比，图5和图6分别为三种算法对于三组数据集的F-measure值和AUC值的计算结果。

根据F-measure的定义，F-measure值越大，说明Recall和Precision的值也就越大，算法的挖掘性能也就越理想。从图5中可以看出，本文方法对于三种不同不平衡度数据集，F-measure值均高于其他两种方法，说明本文方法具有很好的挖掘性能。这是由于本文方法在进行数据挖掘之前，进行了聚类和特征提取，消除了一部分的冗余信息，使得挖掘效果更为理想。

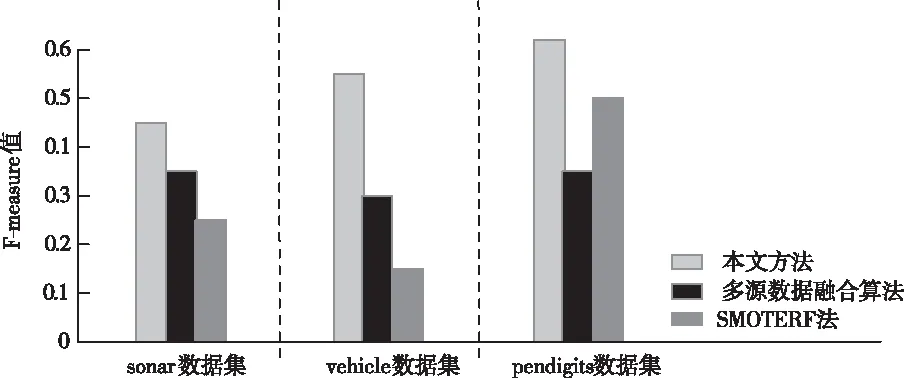
图5 三种方法的F-measure值对比

根据AUC的定义，当结果越接近于1时，说明算法整体的挖掘性能越理想。从图6中可以看出，三种数据集下，本文方法AUC值均高于其他两种方法，说明方法具有的挖掘价值越高。

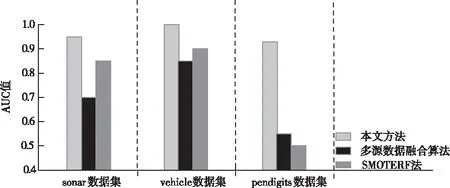
图6 三种方法的AUC值对比

5 结论

考虑到不平衡数据的特点，本文判定并采用过采样处理不平衡阵列，尽可能地去除阵列中的噪声和杂质，使数据趋于平衡状态；然后，对平衡后的数据集进行聚类和特征提取，通过聚类的形式，对不平衡阵列分别进行数据层面和算法层面的调整，以此达到更为理想的挖掘效果。通过进行仿真，结果也验证了所提方法具有优秀的挖掘效果。