多址接入无线传感器网络覆盖控制算法研究

孙晓杰，田 琳

(伊犁师范大学电子与信息工程学院，新疆 伊宁 835000)

1 引言

当多址接入无线传感器网络的运算能力、通讯宽带以及节点能量等均被制约时，运用选择路由或放置传感器节点等方式优化网络各类资源，以此改善网络的通讯、传感及感知等服务水平，此为多址接入无线传感器网络的覆盖控制手段[1，2]。通过恰当的覆盖控制方式，可有效提升网络的服务水平、降低网络整体能耗、均衡各节点能量并延长网络的使用寿命[3]。

感知概率模型下的传感器覆盖算法是通过感知概率模型，确定概率阈值及各节点的感知距离界限，依次排序各节点后，构成概率覆盖实现覆盖控制。该算法可适度均衡各节点能量，但因实际使用中控制精度的制约，降低网络能耗的效果有限[4]；非合作博弈的无线传感器网络覆盖控制算法是通过余下能量及节点覆盖率建立收益函数，并为各节点挑选恰当的运行方式实现网络拓扑的构造，基于此结合非合作博弈理论建立覆盖控制算法实现对网络的覆盖控制。该算法可为网络节点提供恰当的覆盖率，但在降低网络整体能耗方面效果稍差[5]。

基于以上分析，本文研究一种结合布尔感知模型与概率感知模型的多址接入无线传感器网络覆盖控制算法。

2 多址接入无线传感器网络覆盖控制算法

2.1 基于布尔感知模型的冗余节点判别与检测

因多址接入无线传感器网络内的节点部署具有较强的随机性，极易产生存在感知覆盖的重叠区间，因此，需采用冗余节点判别的方式检测出冗余节点，并令此类节点休眠，以此将传感器网络的使用寿命延长[6，7]。在此选用布尔感知模型，实现冗余节点的判别与检查。设定多址接入无线传感器网络内节点i的覆盖区间用D(i)表示，其运算式为

D(i)={E∈A|d(E，Di)≤r}

(1)

式(1)中，检测区间面积与此区间中的点分别以A和E表示；节点i的位置以Di表示；点E与Di之间的欧氏距离以d(E，Di)表示。

如图1(a)所示，节点i、j重叠覆盖区间为图中阴影部分，针对节点i而言，若它的覆盖区间符合下式

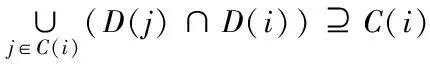
(2)

式中，与节点i相近的邻节点集合用C(i)表示，即与该节点之间的间距不超出节点感知半径r的节点集，该集合可表示为C(i)={j∈C|d(i，j)≤r，j≠i}，所检测区间中的节点集用C表示，节点i、j间的欧氏距离用d(i，j)表示。当节点i的覆盖区间符合式(2)时，那么此节点即为冗余节点，可令其步入休眠状况。

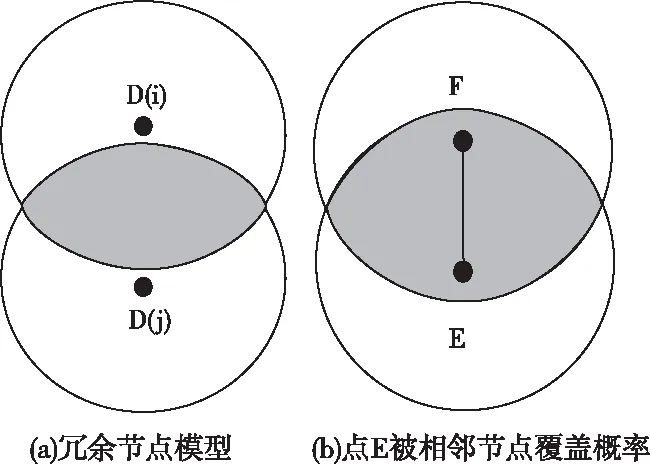
图1 冗余节点判别检测模型

如图1(b)所示，假设节点F覆盖区间中的随机一个点为E，点E与节点F之间的间距以变量X表示，那么其取值区间与概率密度函数分别用0≤x≤r与fX(x)=2x/r2表示。由节点F的相邻节点覆盖点E的期望值运算过程为

1)假设节点F的相邻节点覆盖点E的概率用p(x)表示，若节点F所具备的相邻节点数目为m个，那么此类节点覆盖点E的概率表示为1-(1-p(x))m。

2)图1(b)中阴影区间为半径为r，对图1(b)中阴影区间的面积实施运算：设节点F距离节点E的间距用|FE|=x表示，其中0≤x≤r。运算所得阴影区间的覆盖面积D可表示为

(3)

3)节点F的相邻某节点覆盖点E的概率为p(x)，对p(x)值实施运算

p(x)=D/πr2

(4)

若节点F的相邻节点数量为m，那么此类节点覆盖点E的概率期望值G的运算式为

(5)

在此设置冗余节点的判别规则为当某个节点可以被大于等于三个的相邻节点覆盖时，即可判别此节点属于冗余节点[8]，以此为依据检测无线传感器网络目标区间内的冗余节点，并使此类节点停止运行开始休眠。

2.2 基于概率感知模型的覆盖控制算法

在以上冗余节点休眠的基础上，结合概率感知模型的覆盖控制算法，实现高精度的网络覆盖控制。将经过冗余节点休眠后的网络目标区间作为此部分的目标感知区间。

2.2.1 目标感知概率模型

通过与x轴、y轴平行的一些直线将多址接入无线传感器网络的目标感知区间划分成m×m的网格，则网格点数量为m2个，m2行m2列的矩阵即为传感器感知矩阵，该矩阵用B=[qij]表示，其元素数量为m4个。若无线传感器网络目标感知区间内的节点总数为N(N≤M)个，同时各节点可单独感知目标，那么i网格点目标的被感知概率可表示为

(6)

式(6)中，节点集合数量用a表示；网格点用k表示；M=m2，且i=1，2，…，m。

2.2.2 覆盖控制算法

基于概率感知模型的覆盖控制算法的关键在于构建感知力较强节点覆盖集与不易被感知到节点覆盖集，结合两个覆盖集，实现对多址接入无线传感器网络的覆盖控制。

1)覆盖概率极限

设目标被感知到的最低概率(即概率极限)用Nmin表示，也就是在Hi大于等于Nmin时，即为目标i被感知到。其中多址接入无线传感器网络的现实使用环境、服务质量需求与软硬件条件等均能够影响到Nmin值的确定，用户可指定该值。

2)感知力较强节点覆盖集的构建

此部分主要针对运行次数少，同时感知力强的节点，在各周期内首先将此类节点唤醒，并构建覆盖集以保障传感器网络的覆盖需求。感知力强节点的运用能够将覆盖集节点的数量降低；运行次数少的节点其所拥有的能量更多，唤醒此类节点运行，休眠能量少的节点可实现传感器网络的能量均衡，避免部分能量少的节点功能丧失[9]。使用此覆盖集实施覆盖控制算法所需实现的目标为：以预先设置的规则为依据，将充足数量的节点唤醒，此类节点的覆盖能够达到无线传感器网络的覆盖需求，也就是全部网格点位置的目标被感知到的概率均大于等于Nmin。可表示为

Bi=qi1+qi2+…+qiM

(7)

式(7)中，Bi值越高则节点i的感知力越强，在未执行算法时运算此值，并将其输入到各周期运算内。一个完整周期覆盖集的运算步骤如下：

①将B、Bi、Nmin、M及m(i)(i=1，2，…，N)输入，其中，m(i)代表节点i的运行次数。

②对节点唤醒次序表实施运算：以之前运行周期所提供的各节点运行次数为依据，向某个集合内归类同样运行次数的节点，同时对归类后的各个集合依据运行次数由少至多排序[10]。如果集合数量总计为u个，集合以Ui表示，其中i=1，2，…，u，各集合Ui内的节点均具有统一的运行次数，同时集合Ui内的节点运行次数比Ui+1低。按照由高到低的次序依次排列集合Ui内各个节点的感知力，可表示为Bi1≥Bi2≥…≥Biai，其中，ai代表集合Ui内节点的数量。基于此所获取到的节点唤醒次序表融合了感知力与节点运行次数，可表示为：

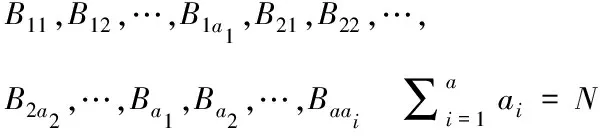
(8)

为方便运算，可简化式(8)为B1，B2，…，BN。

③基于以上两步骤对此部分覆盖集实施求解，求解过程为：a.初始覆盖节点集属于空集，将此部分节点依据次序表依次向此空集内加入；b.以节点i为例，向覆盖集内加入节点i，依据此节点的运行次数，对覆盖集内节点i运行时网格点k位置目标被感知到的概率Hk实施运算；c.如果min1≤k≤M{Hk}≥Nmin，则运算结束，输出此部分节点覆盖集。

3)不易被感知节点覆盖集的构建

此部分重点针对运行次数少，但所处网格点位置不易被感知到的节点，在各个周期内首先将此部分节点唤醒，同时构建此部分节点覆盖集。唤醒不易被感知到的节点运行，能够将无线传感器网络的感知概率快速提升。在感知概率模型式(6)中使qki为0，能够在开启其余节点的前提下将节点i位置目标被感知到的概率获取到。在未执行算法时运算此概率值，并将其输入到各周期运算内。此部分单个周期覆盖集运算步骤为：

①将B、Nmin、M、m(i)(i=1，2，…，N)及qki输入。

②此部分节点唤醒次序表的获取：此部分各节点运行次数集合U′i的归类及排序方式与感知力较强节点覆盖集构建步骤②相同，在此基础上，依据由高到低的次序依次排列集合U′i内各节点网格点位置目标的被感知概率，可表示为qi1≤qi2≤…≤qiai，其中，ai代表集合U′i内节点的数量。综合以上获取到一个将被感知概率与运行次数相结合的节点唤醒次序表，可表示为：

(9)

为方便运算，简化式(9)为Q1，Q2，…，QN。

③在此基础上获得此部分节点覆盖集，获取过程与感知力较强节点覆盖集构建步骤③中覆盖集的求解过程相同。

结合以上两个覆盖集实现对多址接入无线传感器网络的覆盖控制，若传感器网络内各目标所具备的感知极限不统一，仅需对加入节点时各目标分别能达到自身的覆盖概率极限予以考量。

3 实验结果分析

将本文算法应用于某多址接入无线传感器网络内，对其实施覆盖控制，检验实际应用效果与控制下实验传感器网络的能耗情况。由实验传感器网络内选取出a、b两个区间作为实验目标区间，其中a区间位于实验网络的边缘，其尺寸为60m×60m，此区间内的节点数量为80个，b区间位于实验网络的正中，其尺寸为90m×90m，此区间内的节点数量为180个。

3.1 冗余节点休眠效果检验

设定实验网络的节点传感半径为11m，在a、b两个目标区间中通过本文算法判别并检测出冗余节点后实施冗余节点休眠，对比休眠前后两个目标区间的覆盖变化情况，如图2所示。

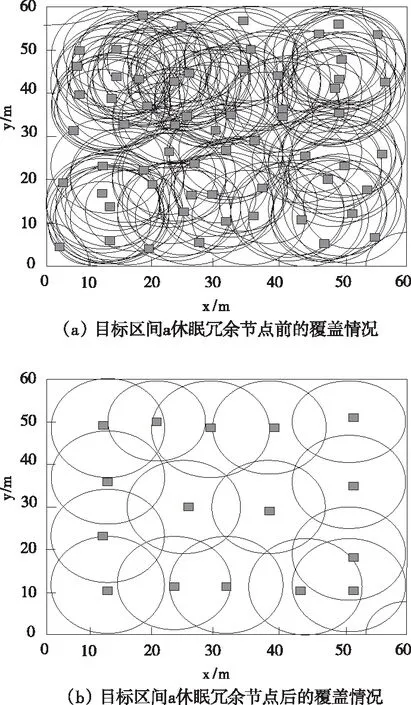
图2 本文算法休眠冗余节点前后各目标区间覆盖情况

由图2可看出，在未采用本文算法休眠冗余节点时，两个不同数量节点的目标区间内的覆盖程度均较高，存在过多的冗余节点干扰，应用本文算法休眠冗余节点之后，明显降低了两个目标区间内的冗余节点数量，且两个目标区间内的覆盖程度均得到显著改善，与此同时保证了两个目标区间均得到覆盖，由此可见，本文算法可通过休眠冗余节点控制无线传感器网络的覆盖程度，控制效果明显。

3.2 目标区间整体能量消耗控制效果对比

此实验中所需用到的对比对象包括感知概率模型的传感器网络覆盖算法(文献[4]算法)、非合作博弈的无线传感器网络覆盖控制算法(文献[5]算法)以及单位时间目标区间的整体能量消耗上限值与下限值。以目标区间b为例，该区间内运行节点的单位时间所消耗能量以We表示，在该区间内全部节点均处于运行状态时，此区间具有最高的单位时间整体能量消耗，由于该区间的节点总数量为180个，则其单位时间整体能量消耗的上限值可表示为180We。下限值的运算过程为：在某个目标仅存在单个节点覆盖的情况下，为了令该目标的覆盖概率达到极限，那么有

e-σ(r2-r1)≥Nmin

(10)

式(10)中，同传感器物理性能相关的可调类别参数以σ表示。该式可改写为

(11)

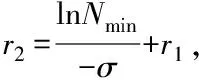
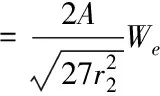
(12)

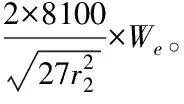
图3 各算法控制下目标区间b的单位时间整体能量消耗

分析图3能够得知，三种算法控制下目标区间b的单位时间整体能量消耗均高于理想下限值，其中非合作博弈算法控制下的能量消耗值最高，且在不同感知概率极限下几乎无变化；本文算法与感知概率模型算法控制下的能量消耗均随着感知概率极限的升高而呈现上升趋势，但本文算法的上升幅度相对更小，且能量消耗更低，原因是本文算法结合了布尔感知模型与感知概率模型，控制更加细腻且精度更高，能够减少节点的唤醒数量，更大的节约了网络能量消耗。

4 结论

本文针对一种多址接入无线传感器网络覆盖控制算法展开研究，通过结合布尔感知模型与感知概率模型，在对网络内冗余节点实施判别检测后，在休眠所检测出冗余节点的基础上，运用感知概率模型覆盖控制算法，分别构建感知力强与不易被感知的两个覆盖集，实现对多址接入无线传感器网络的覆盖控制。实验结果表明，本文算法可有效休眠冗余节点，控制无线传感器网络的覆盖程度，控制效果明显；在本文算法的控制下，网络的目标区间单位时间整体能量消耗较低，达到节约无线传感器网络能耗的效果，为延长多址接入无线传感器网络的使用寿命提供帮助。