基于卡尔曼和最小二乘的抗野值降噪方法研究

朱红运，庞建国，先治文

(中国人民解放军63729部队，山西 太原 030000)

1 引言

在工程测试中，由于测量设备本身误差、随机误差和各种环境因素等干扰，使得测量数据存在噪声，部分测量数据还会包含有严重偏离目标真实值的数据，通常将这些严重偏离目标真实值的数据称为“野值”。根据是否连续，野值可分为孤立型野值和连续型野值[1]，孤立型野值表现形式是孤立的点，而连续型野值则成片出现，也称为斑点型野值。在对测量数据降噪时，野值会给降噪结果带来很大的误差，甚至会使信号严重失真。因此，为获取有效测量数据，需采用鲁棒性强、滤波精度高的降噪方法，对原始数据进行降噪，并将野值剔除或进行必要的修正。

卡尔曼滤波作为线性高斯系统的最优滤波算法，具有理论基础完备、计算简便等优点，已广泛应用于测量数据的降噪处理[2-3]。传统的卡尔曼滤波鲁棒性相对较差[4]，为进一步提高其鲁棒性和滤波精度，许多学者对卡尔曼滤波算法进行了改进。文献[5-7]在传统卡尔曼滤波算法的基础上，通过引入调节因子，设计了一种自适应卡尔曼滤波算法，提高了卡尔曼滤波器的抗野值干扰能力，但上述方法在选取调节因子时还需要依靠经验；文献[8]提出了一种能动态调整抗野值门限的自适应卡尔曼滤波算法，该方法可根据信号变化率自适应调整抗野值门限，有效降低野值的影响；当野值连续出现时，虽然该方法门限能够自适应调整，具有一定的抗连续型野值干扰能力，但由于相邻野值的变化率是随机的，在抗野值门限调整时必然会存在一定的误差；文献[9]提出了一种基于最小二乘和卡尔曼滤波的跟踪定位算法，其首先采用最小二乘法对目标点进行估算，而后使用卡尔曼滤波算法对估算值进一步修正，实现了高精度跟踪定位，但该方法需要对每个观测值进行拟合，随着数据增多，拟合误差会逐渐增大，对连续型野值的抗干扰能力有限。

鉴于此，为有效降低野值对滤波的影响，提高卡尔曼滤波精度，本文提出了一种基于卡尔曼和最小二乘的抗野值降噪方法，该方法在进行卡尔曼滤波过程中，采用最小二乘拟合方法对野值进行修正，并通过引入调节因子降低连续型野值拟合误差的影响，提高其抗连续型野值干扰能力，最后通过仿真验证了该方法的有效性。

2 卡尔曼滤波算法

卡尔曼滤波算法基本原理是求动态系统状态序列的线性最小方差误差估计，利用动态的状态方程和观测方程来描述系统。其在滤波过程中，首先建立描述随机动态变量随时间变化的先验模型，而后在实时观测随机变量基础上，根据前一次估计值即可推导出当前目标状态的最优估计值。

首先，使用系统的状态方程和观测方程来描述需要测量的系统

X(k)=A·X(k-1)+B·U(k)+w(k)

(1)

Z(k)=H·X(k)+y(k)

(2)

式中，X(k)、X(k-1)分别为k与k-1时刻系统的状态；A、B分别为系统状态转移方程和控制方程；w(k)为协方差为Q的系统噪声；Z(k)为k时刻系统的观测值，H为观测状态转移矩阵，y(k)为协方差为R的观测噪声。

预测方程为

X(k|k-1)=AX(k-1|k-1)+BU(k)

(3)

P(k|k-1)=AP(k-1|k-1)AT+Q

(4)

式中，X(k|k-1)为k-1时刻对k时刻系统状态的预测；P为误差协方差，P(k|k-1)为k-1时刻对k时刻误差协方差的预测；AT为A的转置。

而后对状态方程进行修正，具体如下

Kg(k)=P(k|k-1)HT/(HP(k|k-1)HT+R)

(5)

e(k)=Z(k)-HX(k|k-1)

(6)

X(k|k)=X(k|k-1)+Kg(k)e(k)

(7)

P(k|k)=(I-Kg(k)H)P(k|k-1)

(8)

式中，Kg(k)为k时刻卡尔曼增益，e(k)为k时刻残差序列，X(k|k)为滤波后的状态值，至此完成一次完整的卡尔曼滤波。

当滤波达到稳定状态时，e(k)为零均值服从正态分布的随机序列，此时滤波精度较高。假设k时刻前观测值均正常，在k时刻出现野值，则此时观测方程可表示为

Z′(k)=Z(k)+Δ

(9)

式中，Z(k)与Z′(k)分别为叠加野值前后的观测值，Δ为野值分量。

在野值存在时，残差序列可表示为

e′(k)=Z(k)-HX(k|k-1)+Δ

(10)

由式(7)可知，在求滤波后状态值时，野值分量被放大为原来的Kg(k)倍引入到状态估计中，特别是当野值连续出现时，残差得不到及时修正，会严重影响滤波精度，因而，在使用卡尔曼滤波器进行滤波时，必须对野值进行剔除或修正。

3 卡尔曼滤波与最小二乘拟合的联合应用

3.1 野值判别

由于异常数据会在残差中体现出来，因而通过判别残差是否超过了合理范围即可对野值进行辨识。对于一个服从正态分布的序列，根据高斯理论，其测量值落在[-3σ，3σ]以外的概率不超过0.3%(σ为序列的标准差)，可认为落在该区域以外的值为异常值，这就是莱特准则判别方法，也称为3σ方法。因此可以以3σ为野值判断阈值，残差中落于[-3σ，3σ]以外的观测值即可认为是野值。

当判出野值时，需对野值进行适当的处理，目前常用的方法是直接使用预测值代替野值[7]，但该方法未对预测值进行修正，从而降低了滤波精度，特别是当野值连续出现时，滤波效果会受到严重影响。为此，本文采用最小二乘拟合方法对野值进行修正，以提高滤波精度。

3.2 基于最小二乘拟合的野值修正

设存在n+1个点(xk，yk)，k=0，1，…，n，可求一个m次的最小二乘拟合多项式

Pm(x)=a0+a1x+a2x2+…+amxm

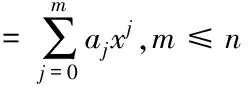
(11)

为求得上式，首先构造满足点(xk，yk)的正交基函数{Qj(x)(j=0，1，…，m)}；其中多项式Qj(x)函数次数不大于m，则Pm(x)可表示为

Pm(x)=q0Q0(x)+q1Q1(x)+…+qmQm(x)

(12)

式中

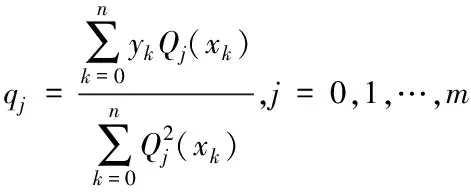
(13)

此时，正交基函数{Qj(x)(j=0，1，…，m)}的递推表达式为

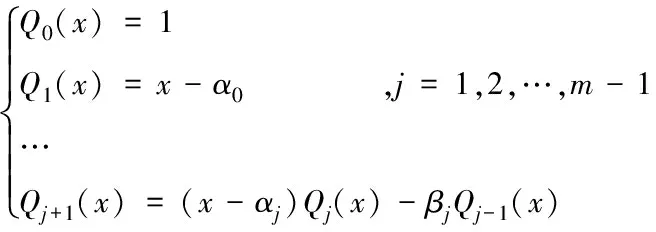
(14)

式中

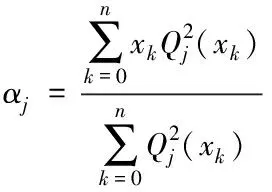
(15)

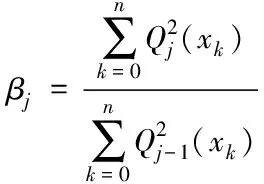
(16)

将m个连续已知的点坐标代入到拟合多项式中，由最小二乘拟合原理得出拟合系数，求得拟合多项式，而后即可利用该拟合多项式外推出下一点的数值。

设k时刻系统的观测值Z(k)为野值，X(k|k-1)为卡尔曼滤波器对k时刻系统状态的预测值，X′(k)为外推拟合值，此时用拟合值代替野值，残差可更新为

e(k)=X′(k)-HX(k|k-1)

(17)

而后将其代入卡尔曼滤波器进行滤波计算，完成单个野值的剔除。

受拟合多项式次数限制，当野值连续出现时，拟合误差会逐渐积累，滤波准确度会随之降低，为保证滤波精度，提高卡尔曼滤波抗连续型野值干扰能力，引入调节因子λ，此时，滤波后状态X(k|k)可表示为

X(k|k)=X(k|k-1)+λKg(k)e(k)

(18)

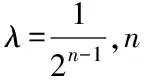
由式(18)可知，随着野值连续个数的增加，λ逐渐减小，即当野值连续出现时，外推拟合值对预测值的修正作用逐渐降低，由此可有效抑制拟合误差带来的影响，提高滤波精度。

综上，本文提出的基于卡尔曼滤波和最小二乘拟合的抗野值降噪方法具体步骤可表述为：

步骤1：对原始信号数据进行卡尔曼滤波计算，求得k时刻残差；

步骤2：采用莱特准则对k时刻残差进行判别，判断该时刻观测值是否为野值；

步骤3：若步骤2中k时刻观测值为正常值，则采用该观测值对卡尔曼预测值进行修正，而后求得最终滤波结果；

步骤4：若步骤2中k时刻观测值为野值，则采用最小二乘方法得出该时刻拟合值；

步骤5：使用步骤4中拟合值代替野值，更新k时刻残差；

步骤6：设计调节因子λ；

步骤7：使用步骤6设计的调节因子对步骤5中更新后的残差进行修正，而后由式(18)求得最终滤波结果。

4 仿真与分析

为检验所提出算法的性能，首先采用传统卡尔曼滤波算法、文献[8]算法、文献[9]算法及本文算法分别对含孤立型野值的含噪仿真信号进行降噪，原始含噪信号及不同算法降噪结果如图1所示。含噪信号信噪比为10dB，其表达式为y(t)=s(t)+n(t)+δ(t)；式中，y(t)为含噪信号，s(t)为幅值为1的原始正弦波信号，n(t)为服从正态分布的噪声序列，δ(t)为孤立型野值，野值分别位于信号第300、500、700及1000个采样点处。

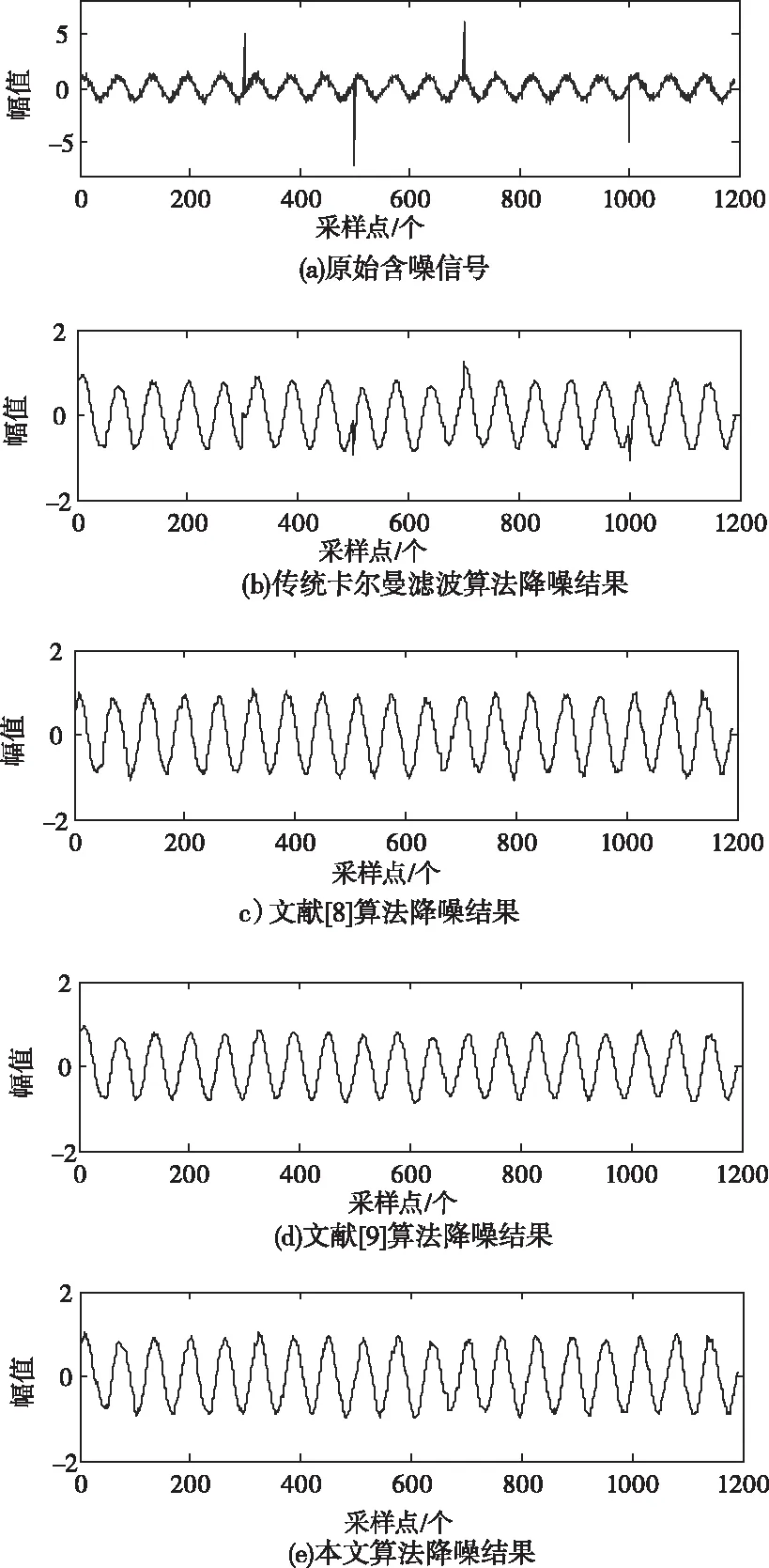
图1 不同算法对含孤立型野值含噪信号的降噪结果

由图1可以看出，上述4种算法对噪声均有一定的抑制作用，但传统卡尔曼滤波算法抗野值干扰能力相对较弱，降噪后信号在野值点处存在一定的失真现象。

为进一步更好的比较各算法的性能，引入噪声抑制率(noise suppression ration,NSR)和信号失真率(signal distortion ration,SDR)两个指标参数进行评估。两指标表达式分别为

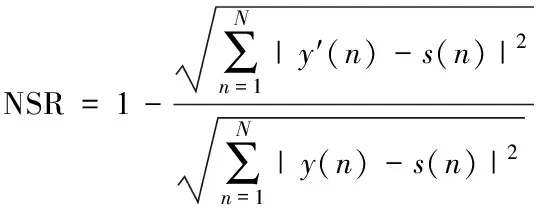
(19)

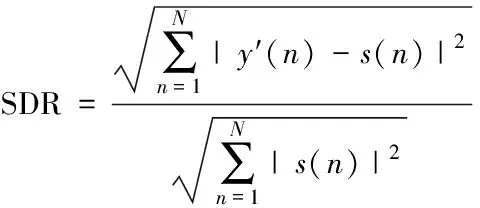
(20)

式中，y′(n)为降噪后信号，s(n)为原始信号，y(n)为含噪信号。

由式(19)～式(20)可知，在采用上述指标评定时，噪声抑制率越大、信号失真率越小，则表明算法的降噪性能越好。不同算法降噪后噪声抑制率(NSR)和信号失真率(SDR)如表1所示。

表1 不同算法降噪后NSR与SDR

由表1可知，与传统卡尔曼滤波算法相比，文献[8]、文献[9]算法对噪声抑制能力更强，但由于文献[9]在进行滤波时，用最小二乘法拟合值代替了观测值，随着数据增多，拟合误差会逐渐增大，导致该方法降噪后信号失真率相比文献[8]更大；本文算法在采用最小二乘拟合时，仅对野值进行了修正，能够有效消除野值的影响，具有最好的降噪性能。

为检验所提算法抗连续型野值干扰能力，在含噪仿真信号中加入连续型野值，而后分别采用上述算法对含噪信号进行降噪处理，原始含噪信号及不同算法降噪结果如图2所示。含噪信号信噪比为10dB，其表达式为y(t)=s(t)+n(t)+δ(t)；式中，y(t)为含噪信号，s(t)为幅值为1的原始正弦波信号，n(t)为服从正态分布的噪声序列，δ(t)为连续型野值(连续6个野值)，连续型野值分别在信号第300、500、700及1000个采样点处开始出现。

图2 不同算法对含连续型野值含噪信号的降噪结果

由图2可以看出，当野值连续出现时，传统卡尔曼滤波算法无法有效降低野值的影响，降噪后信号中仍存在突变点，其余算法降噪后信号在野值对应位置也出现了不同程度的失真。

不同算法降噪后噪声抑制率(NSR)和信号失真率(SDR)如表2所示。

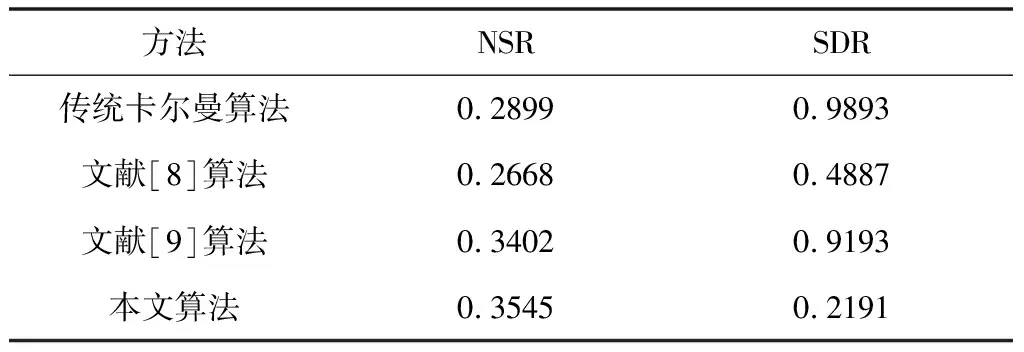
表2 不同算法降噪后NSR与SDR

由表2可知，文献[8]、文献[9]算法降噪性能均优于传统卡尔曼滤波算法，同样由于文献[9]在进行滤波时，用最小二乘法拟合值代替了观测值，随着数据增多，拟合误差会逐渐增大，致使该方法降噪后信号失真率相比文献[8]更大；当野值连续出现时，会对文献[8]设计的自适应抗野值门限造成一定的误差，导致该方法的噪声抑制率低于文献[9]算法；在对连续型野值处理时，本文算法通过引入调节因子，有效降低了拟合误差带来的影响，提高了滤波精度，因而具有最强的抗连续型野值干扰能力。

为进一步验证所提算法的鲁棒性，采用该算法分别对信噪比为10dB、8dB、6dB的含孤立型和连续型野值的含噪信号进行降噪，结果分别如表3、表4所示。

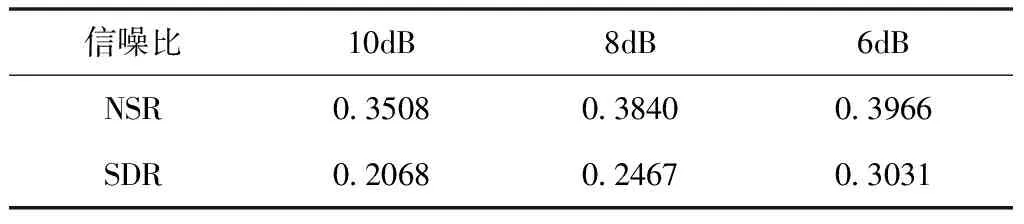
表3 含孤立型野值含噪信号的降噪结果

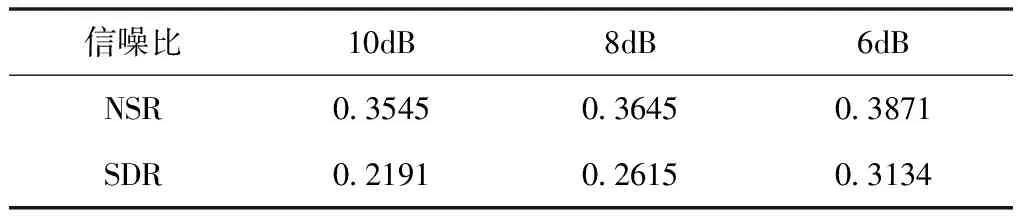
表4 含连续型野值含噪信号的降噪结果

由表3、表4可知，无论野值为孤立型还是连续型，随着信噪比减小，噪声抑制率均逐渐增大，表明本文算法具有较强的鲁棒性，在强噪声影响下仍具有很好的降噪性能及抗野值干扰能力；此外，随着噪声强度增强，由于受噪声影响，降噪后信号失真率缓慢增大，属正常现象，降噪结果表明，当噪声较强时，信号失真率仍可以满足要求。

5 结论

本文提出了一种基于卡尔曼和最小二乘的抗野值降噪方法，该方法在进行卡尔曼滤波过程中，使用最小二乘拟合方法对野值进行修正，有效降低了野值对降噪结果的影响。由实验结果和理论分析可知，在进行卡尔曼滤波时，使用最小二乘拟合值代替测量信号中的野值可有效提高卡尔曼滤波算法性能，降低野值对降噪结果的影响；当野值连续出现时，逐渐减弱野值拟合结果对卡尔曼预测值的修正作用，可进一步提高卡尔曼滤波算法抗连续型野值的干扰能力。