基于DNA随机置换的新型图像加密算法研究

张军朋，向 菲

(1. 河南省网络空间安全应用国际联合实验室，河南 洛阳 471023；2. 河南科技大学电气工程学院，河南 洛阳 471023)

1 引言

随着互联网的快速发展和智能设备的不断普及，人与人之间的交流方式发生了根本性变化。人们可以通过互联网向他人传输文字、图像和视频等文件内容。其中图片具有文字所不能表达的内容，在传输的过程中由于内存比视频文件小，传输速度更快受到人们的喜爱。但是互联网具有开放性和共享性特点，一些需要保密的图片和涉及私人隐私的图片很容易会泄露出去，图像安全越来越受到人们的重视。图像加密技术由来已久，经过长时间的发展，混沌序列加密[1，2]和DNA序列加密[3]等加密方法被提出来。Matthews首次把混沌映射作为加密序列对文本进行加密[4]。Fridrich[5]首次将混沌系统应用到图像加密领域。此后混沌系统经常用在图像加密算法中。常见的混沌加密方式包括利用Logistic混沌系统迭代出混沌序列，对图像矩阵进行置乱、置换和扩散操作。但是低维的混沌系统[6，7]结构简单、空间复杂度低，造成图像加密空间略小，有一定机率会被穷举攻击破解。高维数的混沌系统[8，9]如四维的混沌系统变量更多，空间复杂度更高，用在图像加密中具有更大的空间和更加随机的混沌序列。

DNA分子的并行性和高储存密度具有传统图像加密所不具有的优势，DNA编码技术为图像加密技术提供了新的思路。Adleman[10]提出了关于DNA的计算研究之后为密码学开辟了新的思路，它的并行性、高储存性和低能量损耗受到人们的关注。但是DNA编码运算简单，如果和低维的混沌系统结合，依旧会存在密钥空间较少，安全性不高的缺点。文献[11]提出使用单一的DNA编码规则容易受到选择性明文的攻击。文献[12]设计了一种DNA和混沌系统结合的加密算法，得到的密文相关性较低但是密文和明文的敏感性低。

针对一些加密算法密钥空间较小[13，14]，DNA编码加密方式单一，本文提出了一种基于DNA随机置换的新型图像加密算法，将像素信息和混沌序列改造结合，提高明文与密文的敏感性，得到的序列和明文进行置乱，再利用DNA编码对待加密图像进行随机置换，改变明文像素的位置和本身的数值来隐藏明文信息。最后进行扩散操作最终得到密文图像。混沌系统的初值与明文像素值有关，极大的提高明文与密文的敏感性。通过对图像像素的相关性、直方图、信息熵、差分攻击、密钥空间大小和敏感性进行分析和仿真，结果表明本算法能够抵御统计攻击和差分攻击，具有较高的安全性。

2 混沌系统与DNA编码

2.1 超混沌Lorenz系统

本文采用超混沌Lorenz系统[15]。其动力学方程为

(1)

在上式中a、b、c、r为该系统的控制参数，x、y、z、w为系统的状态变量。当a=10，b=8/3，c=28，-1.52≤r≤-0.06时，系统具有两个正的李雅普诺夫函数，式(1)处于混沌状态。这里取r=-1。

2.2 DNA编码及其运算

DNA主要由四个部分组成：A、G、C、T。它们两两互补，其中A与T、C与G分别互补。将DNA编码互补的原理引入图像加密中，提高图像加密的复杂度。在图像处理的过程中，需要首先将其变成八位二进制的像素矩阵，进而进行处理。二进制中的“0”和“1”互补，由此将“0”和“1”与DNA的两对碱基对应。利用DNA编码的加法运算和减法运算进行图像处理。如表1所示。

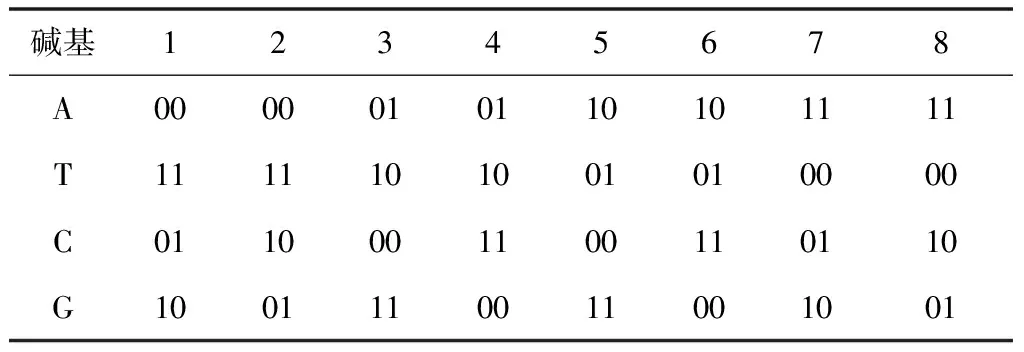
表1 DNA编码规则

由表1可得四个碱基代入到二进制中共有8种编码方式。在进行图像处理时可选取其中一种。图像的像素大小不超过8位的二进制数。8位的二进制数可转化为两对碱基，同理混沌系统经过处理得到的伪随机序列数值最大值也不超过8位的二进制数，将其每个元素也转化为两对碱基。通过DNA的加法和减法运算对图像进行置换操作。

DNA编码的加法和减法规则如表2、3所示。本文选用第2种编码规则进行编码，加法和减法运算均采用规则2进行运算。图像加密所用DNA运算规则和图像解密运算规则相反。

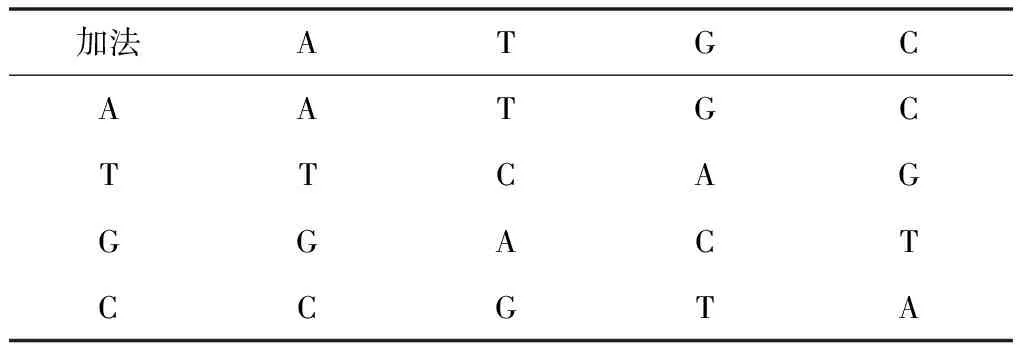
表2 DNA加法运算规则

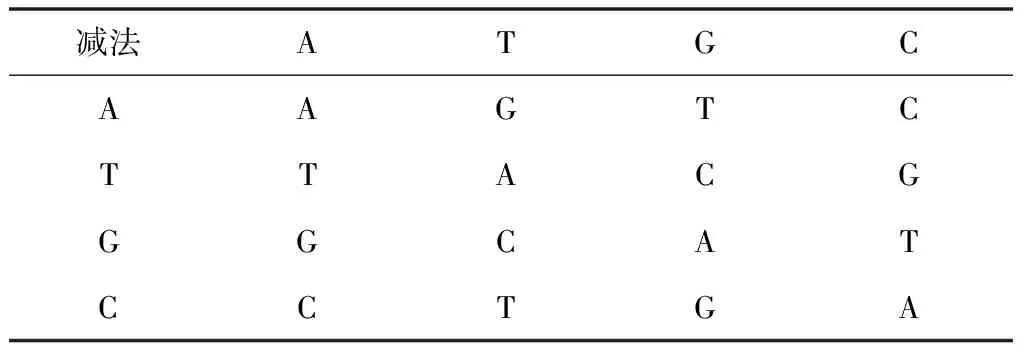
表3 DNA减法运算规则

3 加密过程

本文首先读取目标彩色图片的三个R、G、B三原色像素矩阵。利用混沌系统生成的混沌序列和DNA序列及其加法和减法规则，对目标图像矩阵进行置乱、置换和扩散处理。打乱原图像像素的位置和数值，使密文图像与原图相差甚大，从而保护目标图片传输过程中的安全。具体步骤如下：

1) 使用MATLAB软件读取大小为M×N×3的彩色图像像素矩阵。M为像素矩阵的行数，N为像素矩阵的列数，3为彩色图像的R、G、B分量的三个矩阵。图像位数为8bit，共有256个灰度等级。像素矩阵中的像素值为0-255之间。

2) 将R、G、B三原色像素矩阵按照从上到下从左到右依次排列为一维的行向量，记为R1、G1和B1。

SHT11集成温度和湿度传感器与一体，与单片机结合组成的温湿度测量系统电路简单、体积小，很适合于许多场合下对温湿度的检测。其通过单片机串口输出温湿度及露点数据，经过电平转换器件将数据传送给上位PC机串口上的RS232，再被PC机进行处理，实现远距离对环境温湿度的检测。本系统实现了单点检测，若经过扩展可以实现多点温湿度检测，也可以采用与无线收发射模块将其扩展为无线温湿度检测系统，满足对温湿度无线检测的需要。

3) 设置超混沌系统的初始值x0、y0、z0和w0，利用四阶龙科库塔算法对超混沌系统进行迭代。为了抵消暂态效应，超混沌系统迭代t次后开始取值。得到四个长度为M×N的一维混沌序列。分别为x、y、z和q四个混沌序列。

4) 对得到的四个超混沌序列进行改造，将其变为和原图像素值范围相同的数值。为了加强原文和密文之间的敏感性，将明文像素与混沌系统的初始值关联以增强敏感性。由式(2)得到4个伪随机序列X、Y、Z和Q。由式(3)得到伪随机矩阵U和I。

式(2)

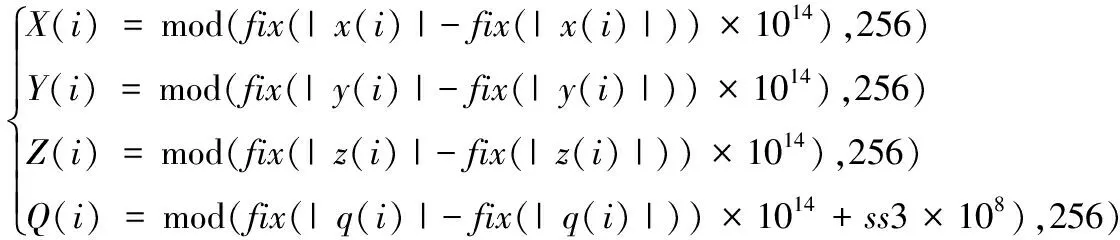
(2)

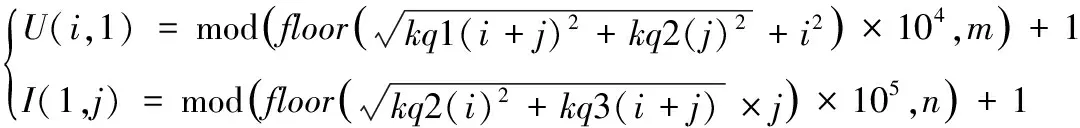
(3)

其中将R1、G1和B1合并为一个向量，并将其分成4段并分别求和对应sx、sy、sz、sq。s是假如明文彩色图像每个像素值为255时像素和。P(i)是明文像素变成一维向量的像素。

mod(x，y)表示x对y的取余运算。fix(x)表示x向0方向取整数。floor(x)表示对x向下取整。

3.1 置乱操作

1) 将Q序列与X序列异或后得到k1，Q序列与Y序列异或后得到k2，Q序列与Z序列异或后得到k3。使用sort(x)排序函数对k1、k2、k3按照从低到高的顺序排序，得到一个新的序列和索引值，将索引值作为置乱的向量分别对R1、G1、B1置乱。

2) 将第一次置乱后的R1、G1、B1向量变为M×N的矩阵。对式(4)的6个变量进行顺序排序，将(rm1，rn1)、(gm1，gn1)、(bm1，bn1)的索引值当做R、G、B分量的置乱向量，进行第二次置乱。得到R2、G2、B2。

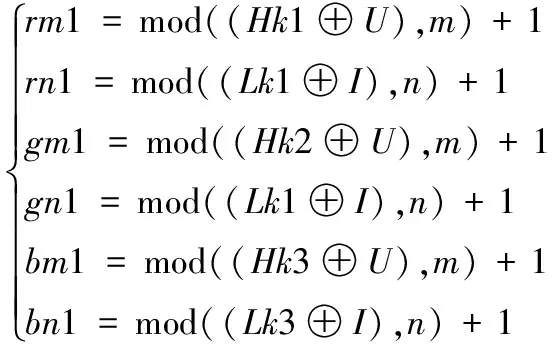
(4)

其中Lk1、Lk2、Lk3分别为k1、k2、k3的列和。Hk1、Hk2、Hk3分别为k1、k2、k3的行和。

3.2 置换操作

1) 将R2、G2、B2三分量分别与k1、k2、k3进行异或，得到R3、G3、B3。此时如果k1为奇数，则对R3分量循环右移k1低三位转化为十进制后的位数。如果为偶数则循环左移k1低三位转化为十进制后的位数。G3分量和B3分量置换方法与R3分量类似。但是G3分量使用k2的数值，B3分量使用k3的数值。

2) 按照DNA编码的规则两对R3、G3、B3分量和kr、kg、kb分量进行DNA编码。先将它们中的每个元素转化为8位的二进制，按从高到底顺序，两两结合为一个DNA的碱基。每个元素得到四个碱基。

3)kr为k1、k2、k3之间的异或。如果kr的最低位为1，将R3分量和kr的碱基按从左向右依次进行相加运算。如果kr的最低位为0，将R3分量和kr的碱基按从左向右依次进行相减运算。将kr和置换后的R分量异或得到kg，对kg的最低位奇偶判断，按照R分量置换原则进行置换。得到的G分量与kg异或得到kb，对kb的最低位进行异或。B分量的置换原则与R分量类似。

R3、G3、B3为DNA规则置换后的R、G、B分量。

3.3 扩散操作

扩散能够加强像素之间的相互影响，当密文图像面对攻击时，攻击者输入稍微与原数据不一样的数据就会得出与原图相差甚远的图像。本文将k1和R3分量按从上到下从左到右变为一维向量。按照式(5)对R3分量进行扩散。R4k是当前像素扩散后的数值，R4k-1是前一个扩散后的数值。R4k-1的初始值r1。其它两个分量扩散方式和R4分量相似。G4k-1初始值r2，B4k-1初始值r3。

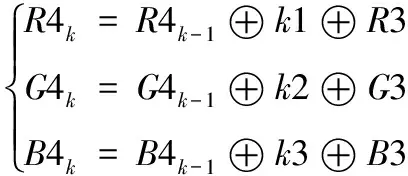
(5)

解密算法是本加密算法的逆过程。

4 仿真结果及安全性分析

4.1 仿真结果

本文加密系统的仿真模拟测试在32位window 7系统，频率为3.40GHz，安装内存为8GB的环境下利用MATLAB 2013a仿真软件对256×256的彩色图像进行加密。混沌系统的初始值为：x0=1.3982×108、y0=9.0634×107、z0=8.4106×107、w0=8.5438×107。混沌系统迭代t=800。扩散中r1、r2、r3的初始值为r1=48、r2=64、r3=48。加密仿真结果如图1所示。明文图像经过加密算法加密后完全掩盖了明文图像，说明加密算法效果良好。

图1 明文与密文图像

4.2 相邻像素的相关性分析

明文图像的像素之间具有很高的相关性，如果密文图像的相关性也很高，攻击者有可能通过像素与像素之间的相关性来破译出明文图像。本文从水平、垂直和对角三个方向检测像素之间的相关性。相关性测试的公式如下。

式(6)

(6)

式(6)中xi，yi为像素的坐标值。ui和vi是相邻的两个像素。rxy为像素相关性的数值。N为选取的像素对数量。由上式对原文图像和密文图像进行测试。图2从像素的行、列和对角三个角度对明文与密文相关性像素进行对比。表4对比了明文图像与密文图像相邻像素相关系数的结果。明文图像的相邻像素的相关系数较大，经过本算法加密之后的密文图像相邻像素的相关性系数数值较小。与文献[16]进行比较，本文算法的相关性更接近零，能够有效降低明文像素之间的相关性。

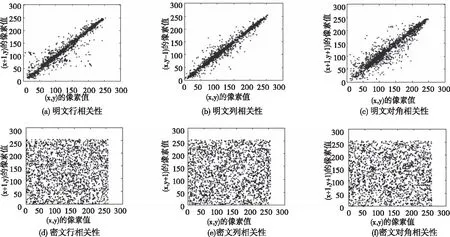
图2 明文与密文相关性对比

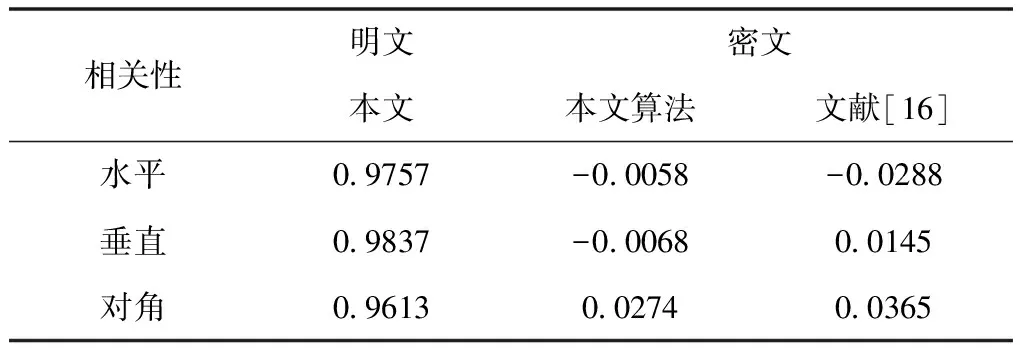
表4 明文图像和密文图像相邻像素相关性数值

4.3 直方图统计分析

图像的直方图是对图像相同的像素值进行统计归纳，以条形图的形式显示出来。一般直方图的横轴为图像像素等级。纵轴为图像像素在每个像素等级的频率。直方图越平稳，图像越能抵御统计攻击。图3为加密前后图像的灰度直方图。由图3可知明文图像的灰度直方图分布很不平稳，而密文图像的灰度直方图分布比较均匀。能够很好的隐藏明文图像的像素信息。

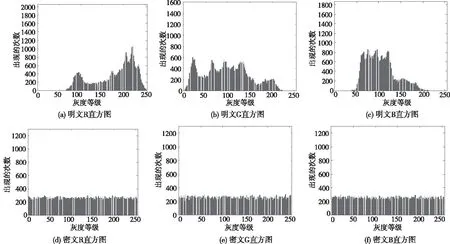
图3 加密前后图像的灰度直方图

4.4 信息熵分析

信息熵反应了图像信息的不确定性[17]。信息熵的值越大，表明图像信息越不稳定。由信息熵公式和本文的图像为8位可知本文的密文和明文图像的信息熵最大值为8[18]。经过本算法加密后的密文信息熵为7.9912，与理想值接近。说明该算法生成的密文图像随机性更好。

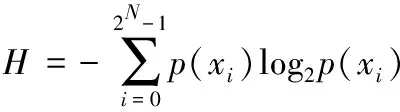
(7)

式中，H为信息熵数值，p(xi)表示灰度值xi在图像全部像素点的比例，N为图像的位数，在本文中N=8。

4.5 差分攻击

差分攻击是通过分析不同的输入对输出的影响进行攻击。一个合格的加密算法要能抵御差分攻击。检测抵御差分攻击的能力主要有两个指标：像素变化率(NPCR，number of pixels change rate)和归一化像素平均改变强度[19](UACI，unified average changing intensity)。这两个指标的计算公式如式(8)式(9)。本文将明文像素的最后一个像素减1，得到新的明文图像，再使用本算法进行加密，得到两个密文图像，并对其进行测试。经测试本算法的NPCR数值为99.60%，UACI的数值为33.45%。对算法的均值做对比，将本算法与文献[20]、文献[21]的NPCR与UACI数值均值的相对误差比较，结果如表5和表6所示，NPCR理想值和UACI理想值的相对误差均为0，本算法的两个数值更加接近理想值，说明本算法具有较强的密钥敏感性，能够有效抵御差分攻击。

表5 NPCR对比分析

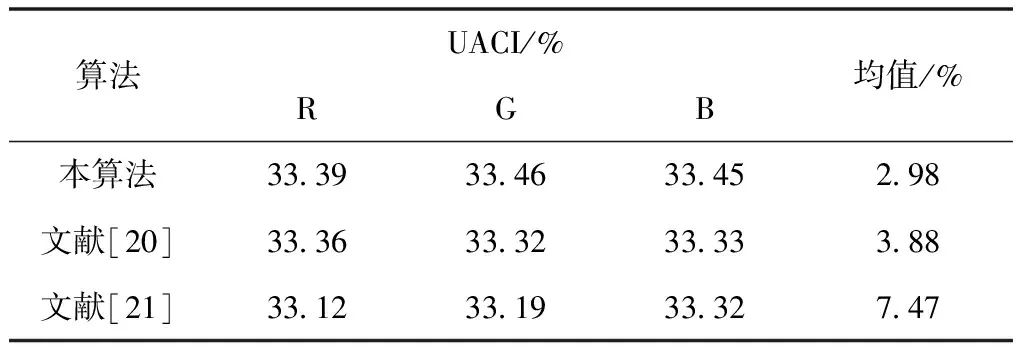
表6 UACI对比分析

(8)

式(8)中M和N为图像矩阵D的行和列，NPCR为像素变化率。

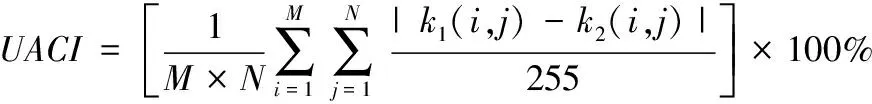
(9)

式(9)中M和N为图像矩阵k1和k2的行和列，k1为改变明文的一个像素点加密后的密文，k2为明文加密后的密文。UACI为归一化像素平均改变强度。NPCR与UACI的理想期望值[22]为99.60%和33.46%。

4.6 密钥空间分析

本文的密钥空间总共由4个混沌系统的初值和4个控制参数组成。其中混沌系统的初值x0、y0、z0、w0和控制参数t为双精度。混沌系统的初值采用精确到小数点后15位的浮点数表示。t为16位无符号整型。3个控制参数r1、r2、r3为8位无符号整型。则本文的密钥空间为1015×1015×1015×1015×216×28×28×28≈1072。对比文献[20]和文献[23]，密钥空间大大提高，如表7所示，该算法能够有效抵御穷举攻击。

表7 密钥空间的对比

4.7 密钥敏感性分析

密钥敏感性分析是对密钥进行微小的改变后，解密算法的敏感性。本算法的密钥精度是双精度，将混沌系统的四个初值分别改动10-15，得到四个明文图像如图4。图a为正确的密钥得出的解密图像，图b为改变x0后的解密图像，图c为改变y0后的解密图像，图d为改变z0后的解密图像，图e为改变q0后的解密图像。图4表明只有正确的密钥才能得到正确的明文图像，说明本加解密算法具有较高的敏感性。

图4 正确密钥和错误密钥解密图

5 结论

本文以混沌序列为基础利用DNA随机编码和DNA随机运算对明文图像进行加密，有效提高了算法的安全性。在求取混沌序列的过程中，利用明文像素值得出超混沌系统的初值，进而得到四个混沌序列，混沌序列贯穿于整个加密算法中，若明文像素改变混沌序列也会相应改变，密文也会改变，提高了密文对明文的敏感性。混沌系统具有随机性，得出的混沌序列也具有随机性，利用混沌序列的随机性对明文进行置乱，能有效打乱原图的像素值位置。DNA算法具有不同的编码和运算方式，使用其中一种方式编码和运算对图像进行置换操作，能够大大提高算法破译的难度。最后在对明文进行扩散，得到一个与明文相差甚远的密文图像。仿真结果表明，该算法密钥空间大，敏感性强，可有效抵抗统计攻击和差分攻击。