一种人机交互执行器的动力学建模及重力补偿

乔 丹，高 阳，倪仕全，田大鹏*

(1. 中国科学院大学，北京 100049；2. 中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；3. 中国科学院航空光学成像与测量重点实验室，吉林 长春 130033)

1 引言

人机交互实现了操作者与机器之间的交互和协作，是当前的一项研究热点[1-2]。在人机交互领域，执行器的设计及其控制问题是影响操作体验的直接因素[3]。为了实现灵活的人机交互，高动态、轻量化、多自由度的执行器设计已成为一项关键问题。

面向人机交互的执行器的机械结构包括串联机构、并联机构、串联与并联混合机构[4-6]。与串联机构相比，并联机构具有结构紧凑、输出能力强的突出优点[7]，在人机交互的执行器设计中得到了广泛应用[8-10]。然而，在现有的设计中，驱动并联机构的运动副通常采用伺服电机结合减速机构来实现，限制了执行器的动态性能。而为了提高动态性能、实现灵活运动的目的，采用电机直驱的方式越来越受到重视。对于直驱方式，执行机构自身的重力会导致外环控制量较大、增益难以提升的问题。对机构的重力补偿控制就成为不得不面对的问题。

并联机构的重力补偿基于对机构进行静力平衡分析[11]，一般有两种方法：机构配重法和基于动力学分析的驱动法。其中，基于动力学分析的方法更加精确，得到广泛的研究。例如，余昆等以Delta并联机构的手控器为研究对象，运用虚位移原理计算出机构在任意位置时的重力补偿力矩[12]。还有将并联机构与串联机构结合的触觉设备为研究对象，采用虚功原理法建立动力学方程，得到重力矩进行补偿[13]。然而，现有的研究多是针对少自由度并联机构开展的，对于采用直驱设计的多自由度并联结构的深入研究十分有限。

本文提出了一种应用于人机交互中动作采集的6-PSS (Prismatic joint-Spherical joint-Spherical joint，移动副-球面副-球面副) 并联机构。该机构采用直线电机直接驱动，避免了减速机构产生的精度损失。采用牛顿-欧拉法对每个构件建立动力学方程，进而得到整个机构的动力学模型。进一步地，从动力学模型中得到重力模型，并基于重力模型建立重力补偿控制器。最后，采用Simulink工具箱对该机构的动力学模型进行了仿真验证。采用弹性阻尼模型模拟人机交互过程，对重力补偿前后的效果进行仿真验证。

2 6-PSS并联机构描述

本文提出的动作采集机构如图1所示。该机构为横置6-PSS并联机构，主要由动平台1、基座6以及六条支链(PSS)组成。每条支链包含上球铰2(S)、连杆3、下球铰4(S)和移动副5(P)。其中，移动副为直驱型直线电机。

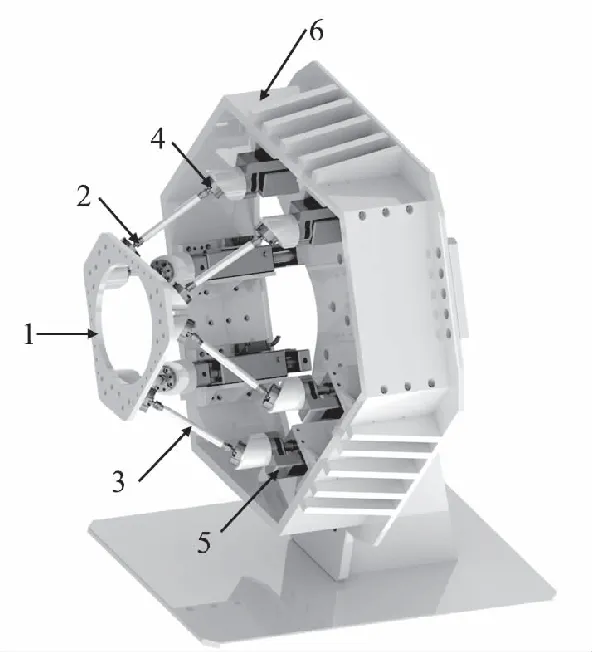
图1 6-PSS并联机构结构图

忽略与动力学无关的几何尺寸，由各运动副中心得到如图2(a)所示的结构示意图。沿连杆方向，以连杆质心作为原点建立各连杆坐标系Si-xsiysizsi。动平台上运动副位置分布如图2(b)所示。其中U1U2U3为等边三角形，以三角形质心为原点建立动坐标系P-xPyPzP，由图中尺寸可确定各上球铰坐标Pi。同理，以图2(c)中等边三角形A1A2A3的质心作为原点建立定坐标系O-xyz，由图中尺寸可确定移动副上的下球铰坐标bi。为了避免移动副所受重力对动力学的影响，本文首次设计了移动副与地面平行的结构。

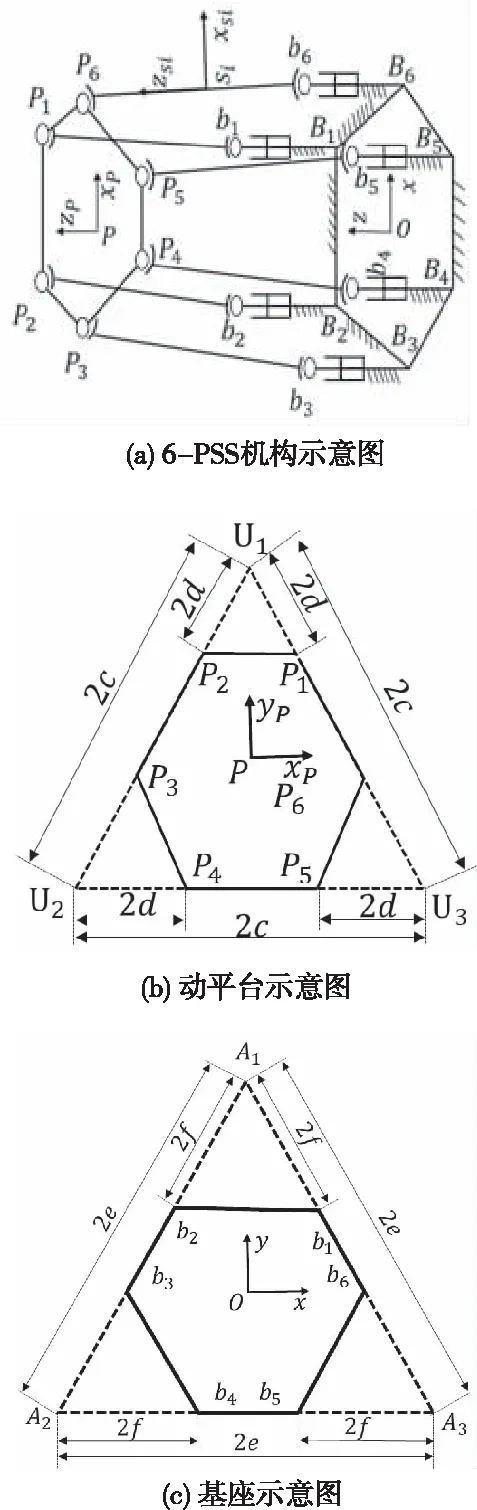
图2 机构位置简图

此外，为了保证机构自由度与运动学可解，动平台与基座的参数设计需满足如式(1)所示条件。

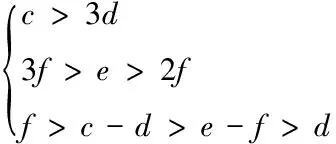
(1)

3 基于牛顿-欧拉法的动力学建模

基于模型的重力补偿需要机构的重力模型。而重力模型包含在动力学模型之中，因此本文首先对机构的动力学模型进行研究。

牛顿-欧拉法建立动力学模型需要对动平台、连杆以及移动副分别建立牛顿-欧拉动力学方程，根据各个构件中力与力矩平衡原则，进而得到移动副驱动力与动平台位姿之间的联系，即逆动力学方程。由于直驱机构的重力远大于摩擦力，因此在分析时忽略摩擦的影响。

3.1 动平台动力学方程

对于本文提出的横置机构，重力沿x轴负方向。动平台承受自身的重力mPg以及第i个连杆的约束力FPi和约束力矩MPi，设动平台受到外力Fext和外力矩Mext。则动平台受力如图3所示。

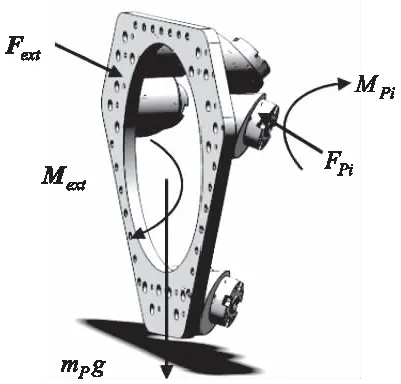
图3 动平台受力图

基于力与力矩平衡，建立动平台的动力学方程为

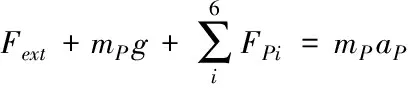
(2)

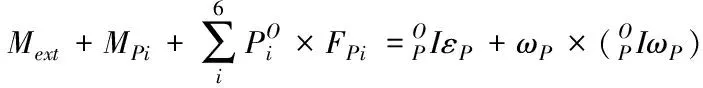
(3)

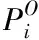
3.2 连杆动力学方程

对于第i个连杆，连杆受到上球铰关节的约束力Fpi和约束力矩Mpi、自身的重力mlg以及安装在移动副的下球铰关节的约束力Fbi和约束力矩Mbi。连杆受力图如图4所示。

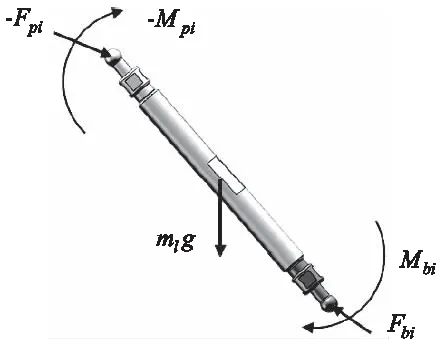
图4 支链受力图

基于力平衡与力矩平衡，建立连杆动力学方程为

-FPi+mlg+Fbi=mlali

(4)

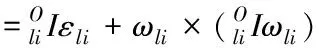
(5)

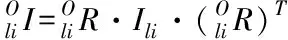
3.3 移动副动力学方程

移动副自身受到下球铰关节的约束力Fbi、自身的重力mbg、基座支撑力FB以及电机对其作用力Fi，见图5。

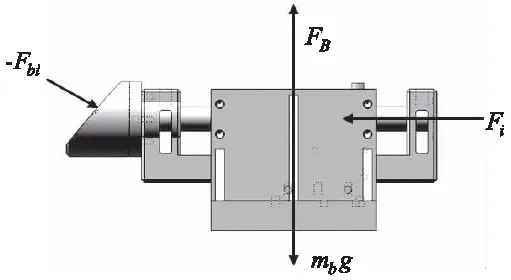
图5 移动副受力图

移动副自由度受到自身的约束，水平方向以外的合力与合力矩均为零。

则水平方向的移动副动力学方程

Fi-Fbi=mbabi

(6)

式中，abi为第i移动副移动的加速度

3.4 整体机构动力学方程

基于文中建立的方程(2)-(6)，在消除各构件的内力后，可建立动平台位姿q=[x，y，z，γ，β，α]T与直线电机驱动力τ=[τ1，τ2，τ3，τ4，τ5，τ6]T之间的动力学关系为

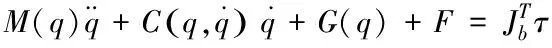
(7)

惯性力的系数矩阵为：

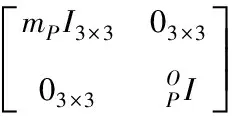
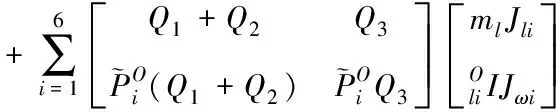
(8)

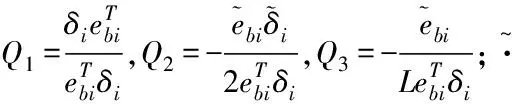
向心力与科氏力的系数矩阵为：

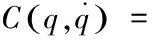
(9)

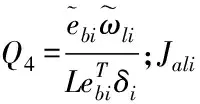
重力项矩阵为：

(10)

完整的动力学模型可用于6-PSS机构的控制方法研究。若仅针对重力补偿问题，式(10)即为目标重力模型。

4 重力补偿

通过逆动力学方程(7)，当机构只受到重力时，保持机构平衡所需的直线电机驱动力为

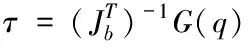
(11)

由此，对移动副设计重力补偿控制器为

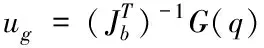
(12)

式中，ug=[ug1，ug2，ug3，ug4，ug5，ug6]T，重力补偿控制器作用于第i个直线电机的控制量为ugi。对每个直线电机设计控制结构如图6所示。

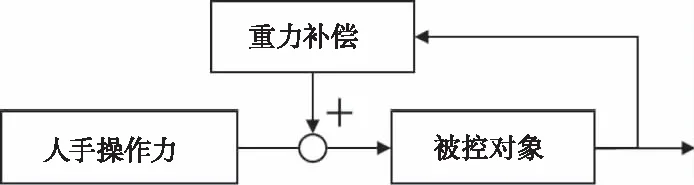
图6 有重力补偿控制结构

得到重力补偿后的系统动力学模型为

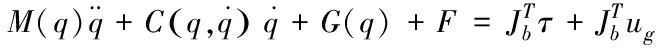
(13)

当动力学模型准确时，存在重力估计值

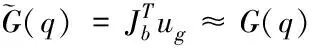
(14)

理想补偿后的动力学模型变为

(15)

因此，在机构操作与控制器设计中，可近似忽略机构横置条件下重力的影响。

5 仿真验证

5.1 动力学模型验证

为了验证机构的动力学，特别是重力模型的正确性，采用Matlab与Simulink对动力学进行验证。在Simulink/SimMechanics工具箱中可以搭建受重力影响的三维机构模型。当给定动平台运动轨迹时，通过逆运动学模型可以得到移动副所需的位移。当移动副模块工作在位置输入、力输出模式下，可解算出移动副到达指定位置时的驱动力。采用上文建立的动力学方程，同样可以计算驱动力。通过对比模型结果与SimMechanics计算结果，即可验证动力学方程的正确性。图7为动力学仿真结构的基本流程图。

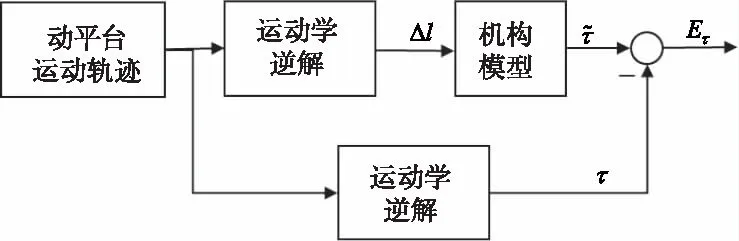
图7 动力学仿真结构

仿真系统中的参数设置如表1所示。动平台中心运动轨迹如式(16)所示。

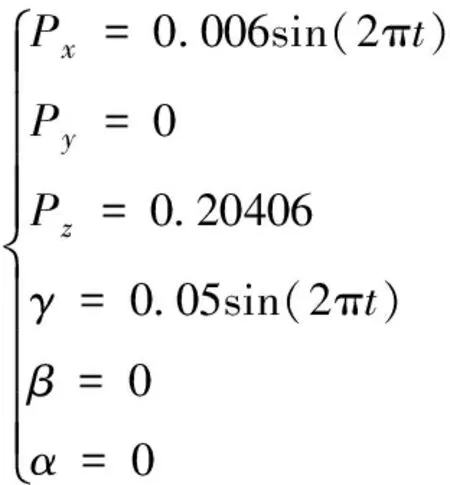
(16)

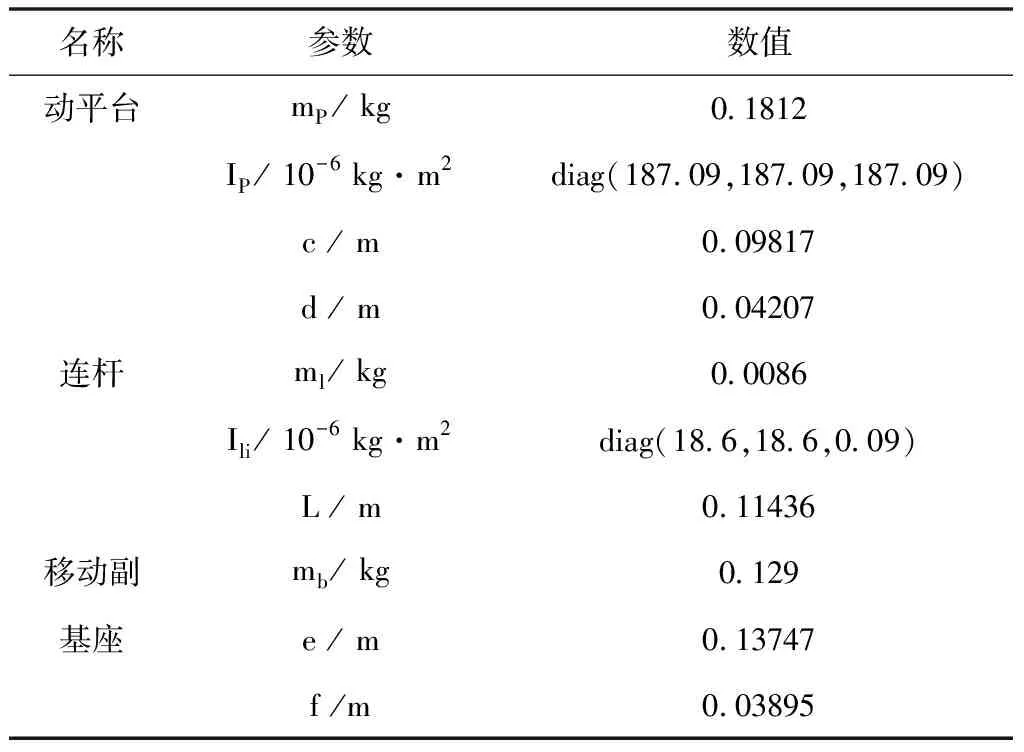
表1 机构的结构参数

为了量化评价模型误差，本文采用相对误差作为动力学模型误差评价标准。相对误差Ei计算如式(17)所示。动平台运动过程中，六个驱动电机的相对误差曲线如图8所示。

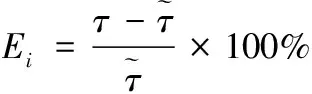
(17)

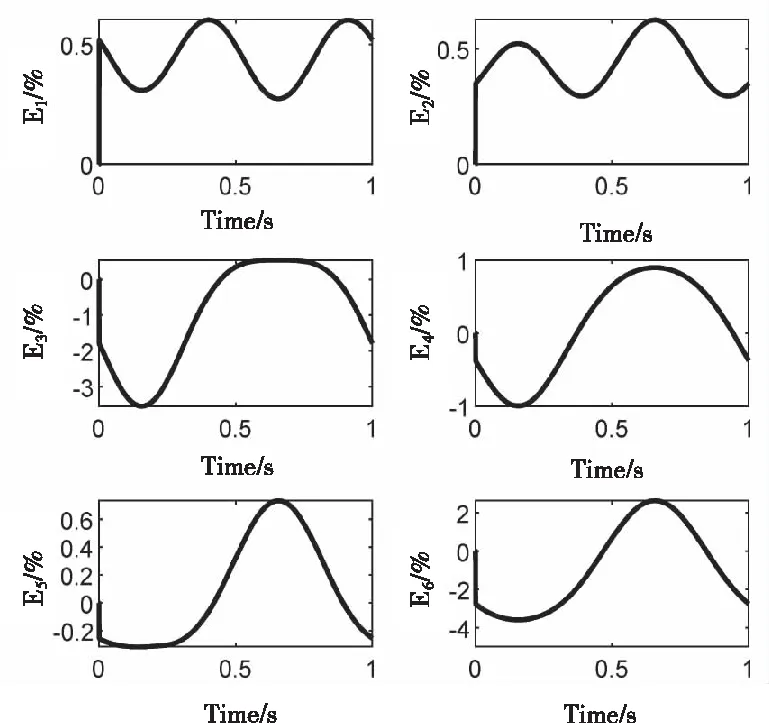
图8 各驱动电机输出力相对误差

仿真结果表明，动力学方程求解结果与仿真结果十分接近，最大相对误差约为3.55%。考虑到模型搭建误差、微分方程解算精度等因素的影响，可认为误差处于容许范围内。基于牛顿-欧拉法的6-PSS并联机构的动力学模型准确有效。动力学中包含的重力模型准确有效。

5.2 重力补偿验证

重力补偿仿真同样在Simulink环境中完成。为了模拟人的操作力，将操作者模型简化为如图9所示的弹性阻尼模型。

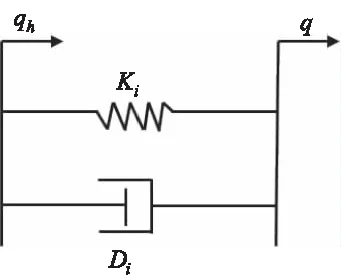
图9 弹簧阻尼模型

在第i个自由度上，由人手操作位姿qh与动平台实际位姿q可以得到人手的操作力为

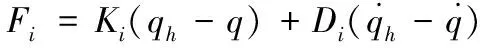
(18)

式中，Ki为第i个自由度的弹性系数，Di为阻尼系数，i=x，y，z，α，β，λ。基于操作者模型，可建立如图10所示的控制系统。

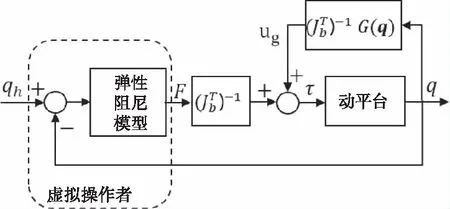
图10 有重力补偿控制系统

采用动平台位姿作为反馈量，在六个自由度分别采用式(18)计算人手控制力与控制力矩。由上文仿真结果可知，动力学模型正确。基于动力学将操作力转换为六个移动副所受到的外力。设置移动副模块工作在力输入、位置输出模式下，可由Simulink得到动平台位姿响应。当仿真程序运行到稳态时，机构姿态q处于操作位姿qh。此时的操作力为克服重力所需的操作力。

仿真选用动平台初始零位作为参考位姿输入。操作者模型参数如表2所示。分别对无重力补偿和有重力补偿的情况进行仿真计算，得到使动平台静止的操作力和力矩如图11所示。

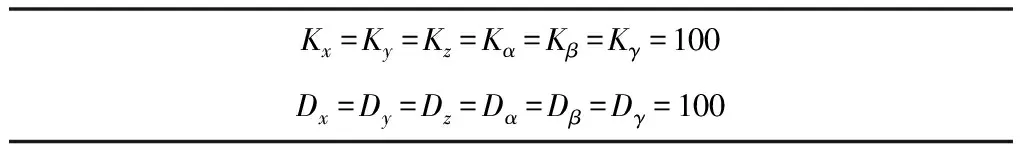
表2 操作者模型参数

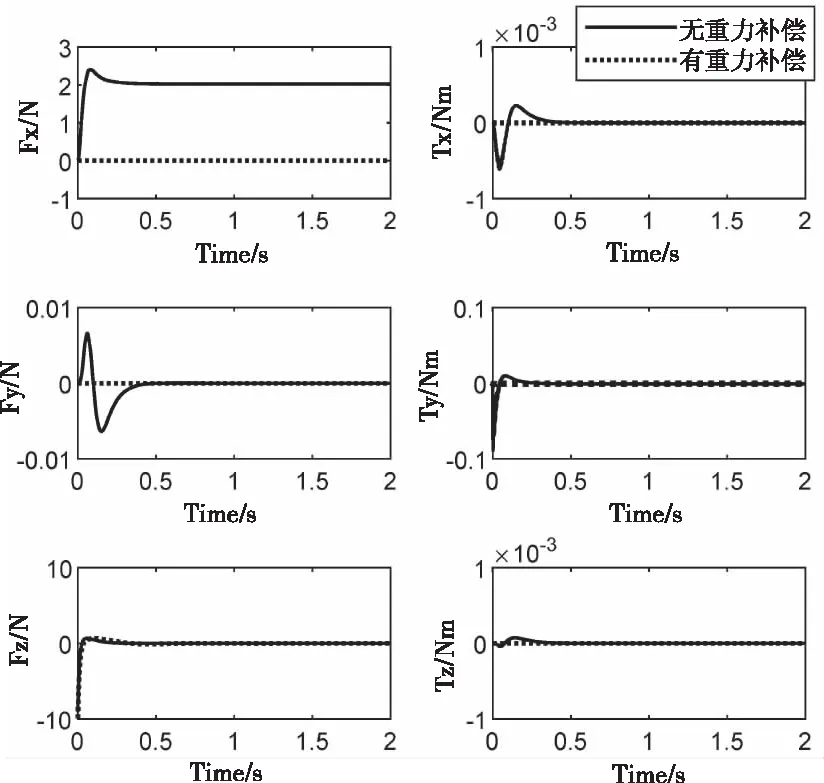
图11 仿真得到的输出力与力矩图

由仿真结果可知：当动平台静止时，在无重力补偿的情况下，操作者需要在x方向施加2N的作用力；而在有重力补偿的情况下，操作力为1.148×10-8N。经过重力补偿后操作力大幅降低，重力补偿有效。

6 结论

本文面向人机交互设计了一种新型6-PSS并联机构。基于牛顿-欧拉法对该机构进行动力学分析，首次建立了横置系统的动力学模型。进一步地，设计了基于动力学模型的重力补偿控制器。仿真验证了所建立的动力学模型的正确性以及增加重力补偿的有效性。为实现高动态灵活人机交互奠定了重要的基础。