基于CHAOS-SVR的COVID-19传播预测模型仿真

刘云翔，肖 岩

(上海应用技术大学计算机科学与信息工程学院，上海 201418)

1 引言

新型冠状病毒肺炎(COVID-19)自2019年年末发现以来，已经夺去了无数人的生命，并产生了巨大的负面经济影响。疫情期间，构建出一个科学的传播预测模型对疫情的防控和政府的统筹是非常重要的[1-3]。

传染病预测模型的研究和分析对理解疾病传播机制发挥着重要作用。疫情发生以来，众多研究人员集中他们的专业知识来开发预测模型，利用共享的数据来分析疫情的流行情况[4，5]。目前预测模型主要集中在传染病动力学及机器学习等人工智能预测模型。动力学模型通过分析传播过程中的相互作用来确定数学公式[6]。汪剑眉[7]等通过改进经典的传染病模型SIR，优化了模型的初始参数、提高了模型精度。改进后的模型分析了干预成效，为后续的防控策略提供了参考意见。范如国[8]等在SEIR模型的基础上使用复杂网络理论对不同状态下的模型参数进行了仿真分析，通过实验对3种不同情形下的新型冠状病毒疫情进行了预测分析并给出了防控建议。人工智能模型利用历史数据进行学习训练。洪彬[9]等在传统动力学模型基础上，使用长短期记忆人工神经网络构建混合模型提高了疫情预测模型的精度，在波动的疫情数据中学习干扰因素。

随着人们对新型冠状病毒肺炎的认知的逐步提高和外界因素的干预，传染病动力学模型需要不断更新模型参数，很难形成一个具有其方程的确定模型。在实际应用中传染病动力学模型对预设参数要求较高且通常求解较为困难，当疫情发生变化时不能及时更新模型参数，影响了预测效果。传染病数据与普通统计数据不同，感染者会将传染病传染给其他个体，因而存在极高的相关性，使得大量基于独立性假设的人工智能预测模型精度降低。此外人工智人工智能预测模型对训练数据的数量和质量要求较高且容易陷入过拟合。疫情发展是一个动态变化的过程，外界的干预甚至会出现重大变化。目前，传统的预测模型，泛化能力差，受其它因素如防控措施、疫苗等外界因素影响大，不能很好的应用在动态变化的新型冠状病毒肺炎疫情的预测中。本文充分考虑到各种外界干预对疫情的影响，提出引入混沌理论进行研究，从整体、变化的角度来分析和预测疫情的发展，将新型冠状病毒肺炎疫情传播预测看作一个长期且动态变化受多种因素共同影响的时间序列预测问题。通过相空间重构技术，在重构的相空间利用支持向量回归推知整个系统的变化，从而提高模型在外界干预情况下的预测精度。基于此，本文提出一种使用混沌理论(chaos theory)结合支持向量回归(support vector regression，SVR)的新型冠状病毒肺炎的传播预测模型(CHAOS-SVR)，实现对动态变化的疫情发展趋势更准确地预测，并且为新型冠状病毒肺炎传播预测模型提供一种全新的思路。

2 CHAOS-SVR预测模型

大量研究表明，传染病的传播是一种混沌现象[10]。混沌是一种无序的，非周期的现象。混沌不是非线性系统简单的无序,本质是确定的，因此存在短期预测的可行性[11，12]。新型冠状病毒肺炎具有非常复杂的传播过程，该传染病具有混沌和振荡的特性[13]。可以使用混沌理论进行研究。

2.1 疫情数据处理

本文使用国家健康卫生委员会公布的数据，建立每日新增确诊人数的时间序列。实验选取新疆2020年7月16日到8月16的疫情数据。选取的新疆疫情从一开始就受到国家的高度关注，有关人员迅速被隔离并及时治疗。因此，该疫情传播过程更加复杂，外界干预和不确定的因素更大。因此选取这次疫情中的数据进行实验。实验以2020年7月16日作为统计的第一天，以一天为时间尺度构建每日新增确诊人数时间序列。新增确诊人数的原始时间序列为ti：i=1，2，…，n,i表示天数，n表示时间序列总长度，ti代表第i天新增确诊人数。

2.2 相空间重构

为了定量地估计系统的复杂性，并估计观察到的动态行为，需要进行相空间重建。从一维时间序列中，可以利用嵌入定理构造一个相空间。设时间序列为{ti：i=1，2，…，n}，时间序列总长度为n，以延迟时间τ为间隔，构成一个m维的向量。其中m=n-(d-1)τ。重构的相空间中的状态向量可表示为：

xi=(ti，ti+τ，ti+2τ，…，ti+(d-1)τ)T

(1)

其中:xi是一个m维矢量，i=1，2，…，m，代表重构相空间的状态序列，d表示嵌入维度。τ是延迟时间。对于一个m维时间序列，重构成的相空间可表示为：

(2)

其中X是d×m的矩阵。d表示嵌入维度。τ是延迟时间。对于实验中延迟时间τ需要进行合理的选取，不能随意假设。如果延迟时间τ选取的过大，会导致疫情数据之间的相关性很小，如果延迟时间τ选取过小，会导致疫情数据相关性较强，淹没其中的隐藏的信息。过大过小的延迟时间都会造成信息丢失。本文使用自相关法来估计疫情数据的延迟时间τ。自相关函数可表示为

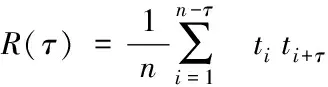
(3)

其中τ是延迟时间，R(τ)表示自相关函数，揭示了相邻两个时刻的相互关联程度。嵌入维度d的选取决定了实验的成败。为了获得更准确的实验效果，本文使用虚假最近邻法计算每日新增确诊人数时间序列的嵌入维度d。吸引子上的轨迹点在相空间中有邻点。这些邻居的行为为了解邻居的演化提供了有价值的信息，以便产生预测方程。另一方面，根据相空间中的邻居的行为能够开发一个简单但有效的算法来确定最优的嵌入维数。

在d维相空间中，状态点xi=(ti，ti+τ，…，ti+(d-1)τ)T，i=1，2，…，n-dτ，和xj=(tj，tj+τ，…，tj+(d-1)τ)2,j∈{1，2，…，n-dτ}之间的欧式距离的平方可以表示为：

Rd，i=‖xi-xj‖2

(4)

其中Rd，i代表相邻状态点之间的欧式距离，不断增大d的值，从最小值开始计算，存在比值Sd。

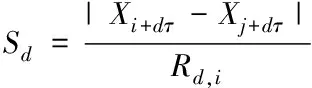
(5)

其中Sd表示嵌入维度增加后到伪最近邻点的比值，当小于百分之五或者不再减少可认为此时的嵌入维度就是最合适的嵌入维度。

2.3 建立CHAOS-SVR预测模型

完成相空间重构后，可以根据重构后的轨迹推导整个系统的变化。可以有效避免复杂系统中未知因素的影响。重构的相空间中，相邻时间依然存在非线性映射关系，实验得到重构相空间中的状态序列{xi：i=1，2，…，m}，存在单步演化规律为

Xi+1=F(xi)

(6)

可改写为

(ti+1，ti+1+τ，ti+1+2τ，…，ti+1+(d-1)τ)T

=F((ti，ti+τ，ti+2τ，…，ti+(d-1)τ)T)

(7)

F(xi)代表非线性映射函数，使用SVR可以很快的学习这个非线性映射。对于给定的训练样本Dtrn={(xi，yi)：i=1，2，…，m}，目标得到一个非线性映射，这就是实验建立的CHAOS-SVR单步预测模型

f(x)=wTx+b

(8)

通过最小化目标函数来优化问题，原目标函数可表示为：

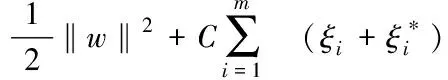
(9)

约束条件为：

(10)

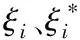
(11)

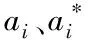
ti+1+(d-1)τ=f(xi)=f((ti，ti+τ，ti+2τ，…，ti+(d-1)τ)T)

(12)

其中f(x)代表相空间中存在非线性映射，SVR模型需要从训练集中学习得到最优的f(x)。对于时间序列{ti：i=1，2，…，n}，n为训练集中样本个数。设置L为待预测天数，CHAOS-SVR模型多步预测算法为

输入：疫情时间序列={ti：i=1，2，…，n}

待预测天数L

算法流程为：

1) 对输入的疫情时间序列进行相空间重构

2) 根据相空间重构结果，建立CHAOS-SVR单步预测模型G：

4) end for

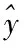
图1 CHAOS-SVR预测模型流程图

3 仿真结果与分析

3.1 实验环境和对比实验

本文所用的编译环境Windows 10 下的python 3.7版本和MATLAB 2014版本。为了更好地比较干预状态下预测模型的精度。本实验设置2组对比实验并进行结果分析，考虑到疫情发展趋势在干预状态下变化大、数据量小，预测模型变得更复杂，传统基于数据的主流预测模型会淹没少数数据，人工智能预测模型和传染病动力学模型分别选择预测效果较好的曲线拟合预测模型和SEIR模型。设置两个规模大小不同的数据集：Set＿15、Set＿20。其中Set＿15 为前15天数据为训练集，Set＿20 划分规则同理。

3.2 实验结果与分析

为避免陷入过拟合，曲线拟合预测模型拟合函数使用3次多项式。图2至图5给出的是不同大小训练集下曲线拟合预测模型和CHAOS-SVR预测模型的仿真结果。

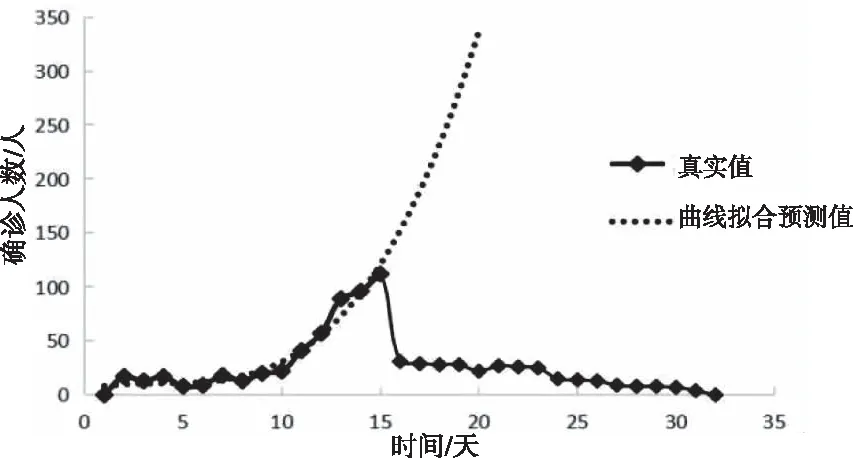
图2 基于曲线拟合预测模型的预测结果(训练集为Set＿15)

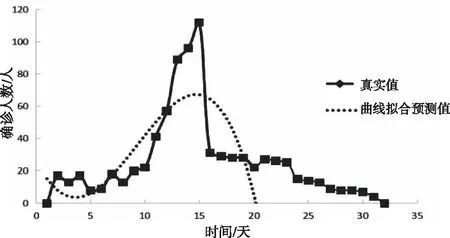
图3 基于曲线拟合预测模型的预测结果(训练集为Set＿20)

图4 CHAOS-SVR预测模型的预测结果(训练集为Set＿15)

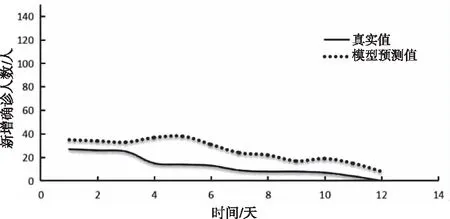
图5 CHAOS-SVR预测模型的预测结果(训练集为Set＿20)

由图2和图3可看出，曲线拟合预测模型能迅速拟合数据，但不能精准预测外界干预状态下疫情的新增确诊人数和走势。这是因为曲线拟合预测模型只是单纯对训练集数据的拟合。当疫情发生重大变化时，曲线拟合预测模型预测精度迅速下降，容易陷入过拟合，甚至出现相反的预测趋势。曲线拟合预测模型与实际误差大与数据集中疫情受到外界干预发生重大变化有关，曲线拟合预测模型陷入对历史疫情数据趋势的过拟合，没有充分考虑到外界因素的影响。由图4和图5可以观察到本文提出的CHAOS-SVR预测模型，在训练集分别为15天和20天的情况下曲线走势都与真实情况大致相同，数值也更接近，这与CHAOS-SVR预测模型充分考虑到干预状态下多种因素的共同影响，以整体、连续的眼光看待疫情的发展有关。

动力学预测模型SEIR模型和CHAOS-SVR预测模型对比结果如图6至图7。

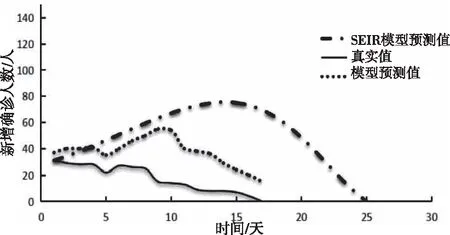
图7 SIR模型和CHAOS-SVR模型对比结果(训练集为Set＿15)

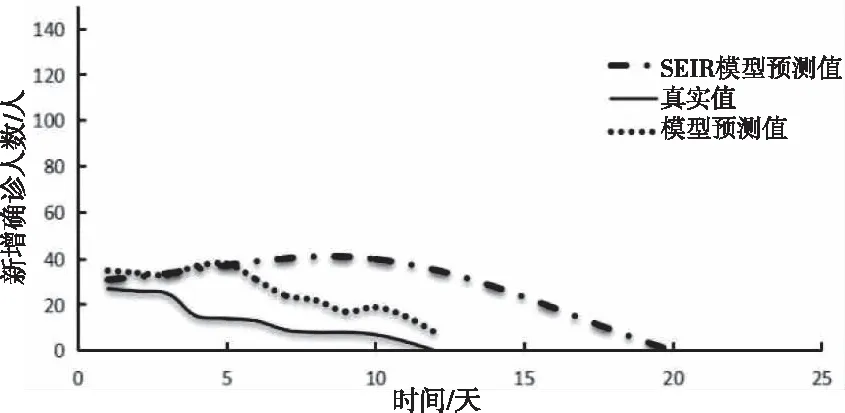
图8 SIR模型和CHAOS-SVR模型对比结果(训练集为Set＿20)

由图6和图7可以看出，在外界干预状态下，本文提出的预测模型预测结果比SIR模型更接近，且在疫情趋势预测曲线上与实际疫情走势基本吻合。而传统的SEIR传播预测模型预测效果误差很大，在训练集为15天和20天都有较大误差。这与疫情发展过程中，模型初期设置的参数发生变化有关。如在SEIR传播预测模型中，参数β代表疾病的传染能力，受外界因素影响很大，随着疫情的不断发展会逐渐变化甚至趋近于零，从而对预测精度造成重大影响。使用均方根误差(RMSE)作为评价指标，3种预测模型的RMSE如表1。本文所提出的CHAOS-SVR预测模型比曲线拟合和SEIR传播预测模型在干预状态下的预测效果更好，在预测数值水平上更接近，均方根误差更小，趋势预测更准确。

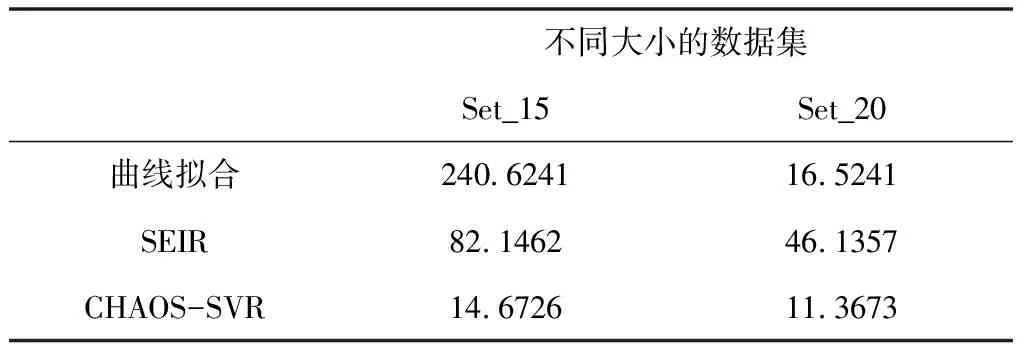
表13 种预测模型的RMSE

4 结语

干预状态下的疫情更加难以预测，其受其它因素影响更大更难预测。基于此，本文提出了一种新的流行病预测模型来预测新型冠状病毒肺炎的传播。引入混沌理论，建立CHAOS-SVR模型进行预测，不断进行递归单步预测从而实现多步预测效果。并和传统预测模型在相同的数据集和干预状态下进行了比较分析，结果表明，本文提出的预测模型在相同干预状态下的疫情数据上具有更好的泛化能力和预测效果，在疫情的防控中具有一定的参考价值，并且为新型冠状病毒肺炎传播预测模型提供一种全新的思路。尽管本文所提出的基于机器学习的新型冠状病毒肺炎传播预测模型较其它模型在相同干预条件下的疫情数据集上的预测效果有了较大的提升，但与真实疫情数据还有一定差距，这与递归进行单步预测造成误差堆积有关，后续将进一步重点研究优化模型，提高单步预测精度，减小多步预测产生的误差堆积。