大型板翅式换热器出口温度均匀性的数值分析

雷 乐，李 楠，赵 波，陶文铨

(1. 西安交通大学能源与动力工程学院，陕西 西安 710049；2. 中国空气动力研究与发展中心设备设计及测试技术研究所，四川 绵阳 621000))

1 引言

板翅式换热器具有结构紧凑、轻巧、传热强度高的优点，被认为是最有发展前途的新型热交换设备之一，因此被广泛应用于石油化工、空分、航空、动力机械和低温领域[1]。随着数值仿真的发展，越来越多的学者[2-6]利用数值模拟的方法对板翅式换热器进行研究。，李新禹[7]等人采用FLUENT软件研究了空气在三角形翅片和不同结构参数的矩形翅片表面的传热与流动性能；王臣[8]等人，对水-空气换热的板翅式换热器典型单元进行了数值模拟，研究了不同的翅片高度对传热性能的影响，得到了优化模型；Liu[9]等人将数值模拟与多目标优化方法相结合，对某液压缓冲器用的板翅式换热器翅片结构参数进行优化，得到了翅片的最优结构参数；Du等人[10]、Aydn等人[11]及Wan等人[12]利用多孔介质方法，建立了全尺寸板翅片换热器的数值模型，研究了全尺寸板翅片换热器的流动传热特性。但所有上述研究中的板翅式换热器都是常规的尺度，本文研究的是一个迎风面积为21m×24m的超大型板翅式换热器，而且对于换热器出口温度场及流场均匀性要求极高。因此，数值模拟成为了唯一的研究手段。本文采用一种基于热校核计算得到的热边界条件，对该超大型板翅式热交换器典型单元进行流动与传热的数值分析，研究其出口段内流场及温度场的均匀性。

2 物理模型

图1为超大型板翅式换热器的组装示意图(迎风面积为504m2)，该换热器是空气和水的交叉逆流换热，其结构分为上下两层共48个板翅式换热器单元(每个单元迎风面积为10.5m2)。

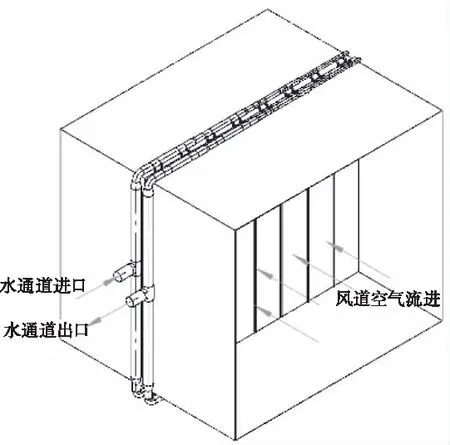
图1 超大型板翅式换热器三维模型

图2所示为包括数个单元的局部组装图。该换热器典型的换热结构是两层空气加一层水，相较于文献中常见的换热器，尺寸十分大，对于这样的结构进行数值仿真会产生十分巨大的网格量，使得仿真无法进行。因此需在整个换热器中选择出代表性单元进行模拟，选取空气侧的典型单元结构，如图3所示。其中包括两层空气翅片，翅片型号为120PZ42055[13]。为便于研究热交换器出口段温度场均匀性，在出口段增加500mm长的延长段。

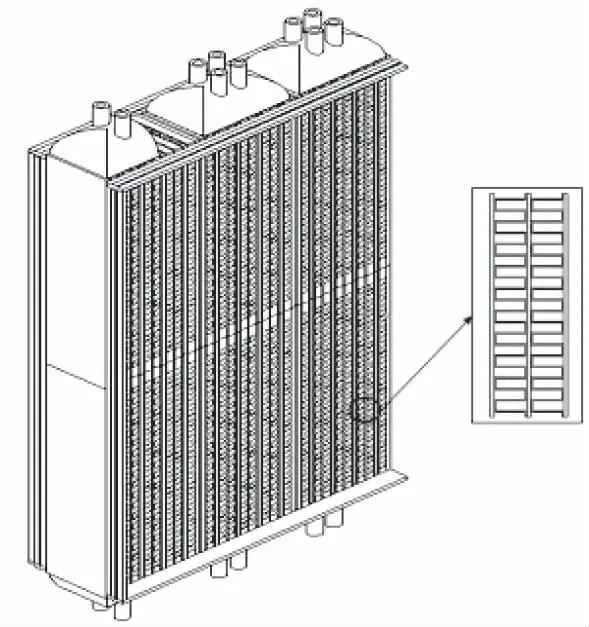
图2 板翅式换热器单元局部组装示意图

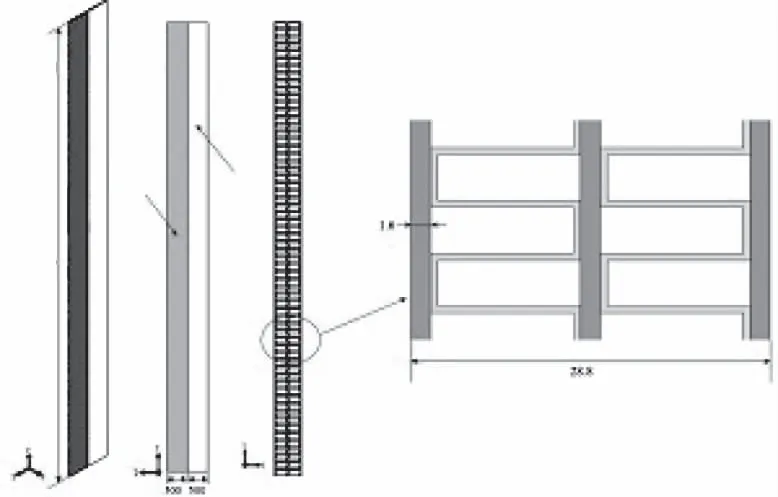
图3 典型单元结构图

3 数值模型

根据空气进口流量和空气翅片的水力直径，计算出雷诺数约为4500，因此采用湍流模型进行数值分析。

3.1 控制方程

数值模拟中选用k-ε湍流模型及标准壁面函数，数值模型的控制方程如下：

连续方程

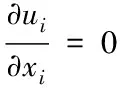
(1)

动量方程

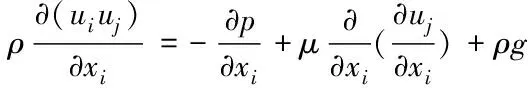
(2)

能量方程

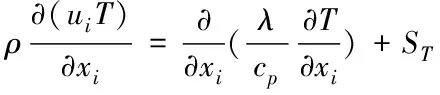
(3)

湍动能方程

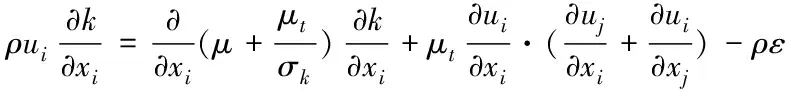
(4)

湍动能耗散率方程

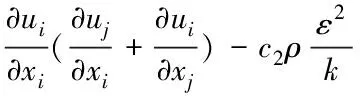
(5)

上述公式中：x为坐标，其中i,j=1，2，3；u为速度分量，m/s；T为温度，K；ρ为密度，kg/m3；λ为导热系数，W/(m·K)；cp为比热容，J/(kg·K)；p为压力，Pa；μ为动力黏度，Pa·s；k为湍动能，J/kg；ε为湍动能耗散率，m2/s3；g为重力加速度，m/s2；μt为涡黏度Pa·s；c1=1.14；c2=1.92；σk=1.0；σε=1.3[14]。

3.2 边界条件

由于本文研究的热交换器是一种空气和水的交叉逆流换热，传热过程的热阻绝大部分在空气侧，为减少数值仿真的网格量，笔者简化掉了水侧的翅片结构，只对空气侧的结构进行建模，因此需要设定一个温度分布函数作为水侧的换热边界条件。其确定方法如下：

1)首先对两层空气和一层水的换热单元进行换热器的传热校核计算。已知空气进口温度Tin，a、水进口温度Tin，w、空气进口流量qs，a、水进口流量qs，w，迭代求解出空气侧和水侧的出口平均温度。其中水侧和空气侧的传热系数计算公式[1，15]如下所示

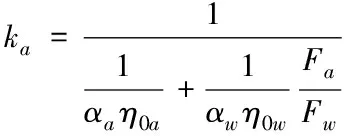
(6)

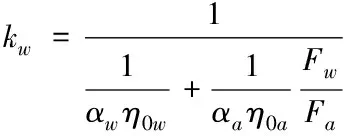
(7)

上述公式中：ka、kw分别为以空气侧、水侧总传热面积为基准时的传热系数；αa、αw分别为空气和水与壁面之间的换热系数，其计算方法如式(8)所示；η0a、η0w分别为空气侧和水侧的翅片壁面总效率；Fa、Fw分别为空气侧和水侧的总传热面积。

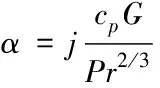
(8)

其中：j为传热因子；cp为比定压热容；G为单位面积质量流速；Pr为普朗特数。

传热校核计算时，根据冷热流体的流动布置，引入互不混合的一次交叉流对数温差修正系数ψ，根据文献[1]，可以获得相应的数值。

2)将换热单元分别沿着x和y方向划分为40份，如图4所示。划分后所得的每一个小单元被认为是一个交叉流的小换热器，同样可以进行相应的传热校核计算。最终通过迭代可以求解出40×40=1600个水侧出口温度值，对这些温度值在x和y方向上分别取节点平均值(如式(9)所示)，得到最终的水侧温度值。

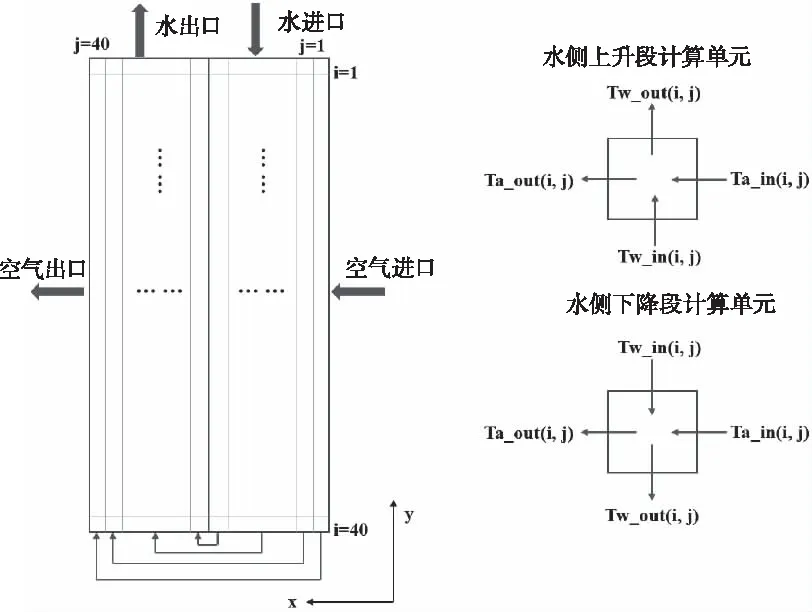
图4 换热单元划分示意图

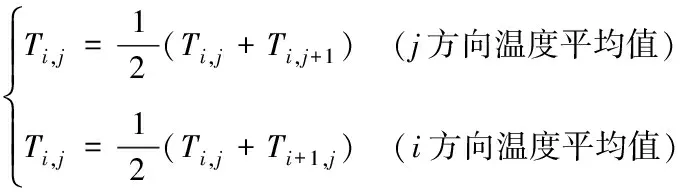
(9)

3)为了将水侧的温度值变换成随坐标变化的函数，将这些数据进行多项式拟合，采取5次多项式拟合以保证拟合精度和拟合结果的准确性。

本文数值模拟所采用的空气进口参数为：空气进口流量3.86 kg/s，进口压力为102.5 kPa，进口温度为344.6K。

拟合得出水侧温度随坐标变化关系如式(10)所示。由于水侧换热系数远大于空气侧的换热系数，可以足够准确的认为水侧的平均温度就是水侧隔板壁面上的温度，故在模拟中将上述所得的温度函数设置为隔板边界上的温度。

T=315.4-28.16x-0.1872y-176.3x2-9.096xy

-0.1738y2+1755x3+29.94x2y-1.229xy2

+0.09814y3+1607x4+102.1x3y-2.206x2y2

+0.2367xy3-0.01699y4-2.205×104x5

-203.7x4y+1.697x3y2+0.1537x2y3

-0.01324xy4+0.0009217y5

(10)

3.3 数值方法验证

为验证数值方法的正确性，对换热器所采用的翅片(型号为120PZ42055)单独进行流动与换热的数值模拟，研究其阻力系数和传热因子随雷诺数的变化。

在Fluent中选用k-ε湍流模型，计算不同雷诺数下的空气进出口压降，计算出阻力系数f与j因子，并将结果与实验值进行比较。在所计算的雷诺数范围(4887-17023)内，阻力系数f的平均偏差为-9.95%；传热因子j的平均偏差为8.25%，证明了数值方法的可靠性。

3.4 换热器典型结构网格系统

对上述典型结构选用Hypermesh软件划分网格。由于翅片厚度只有0.55mm厚，隔板厚度为1.6mm，要在10.5m高度方向上划分较精细的网格，会产生巨大的网格量，因此在翅片厚度方向上划分一层网格，在隔板厚度方向上划分2层网格，最终共计4200万网格。一个周期结构(一个翅片高度方向上的结构)网格及截面网格如图5所示。

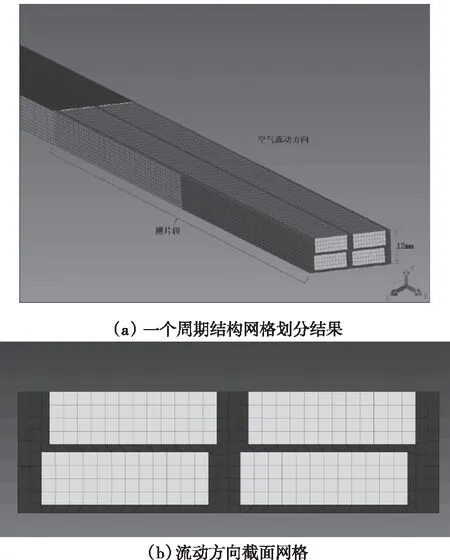
图5 数值模拟用网格系统

4 数值模拟结果与讨论

为了研究不同截面上的温度和湍流度的变化情况，笔者对计算模型选取从空气进口到出口之间的120个截面以及出口截面上Y截线和X 截线(图6所示)进行数据分析。

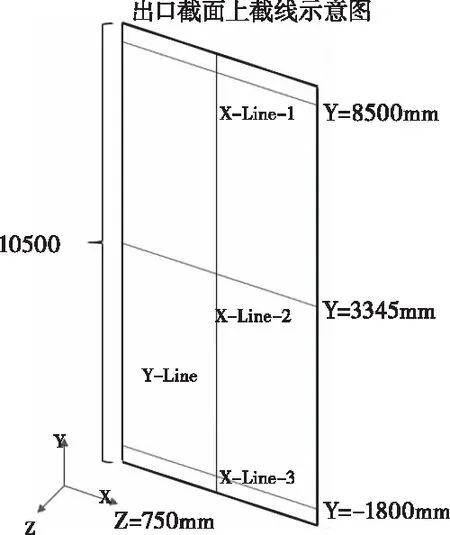
图6 出口截面上X与Y截线示意图

图7为出口截面上Y截线与X截线上的温度分布。从图7(a)中可以看出，在每一个Y高度上空气温度很均匀且呈现左右对称的变化；图7(b)为Y方向上的温度变化，可以看出空气温度虽然沿高度方向空气温度有所变化，但变化范围很小。经过统计，空出口平均温度为316.98K，进出口温度差为26.36K。空气出口的最大温度为319.19K，最小为317.10K，温度场不均匀性(最大与最小温度之差)为2.07K。

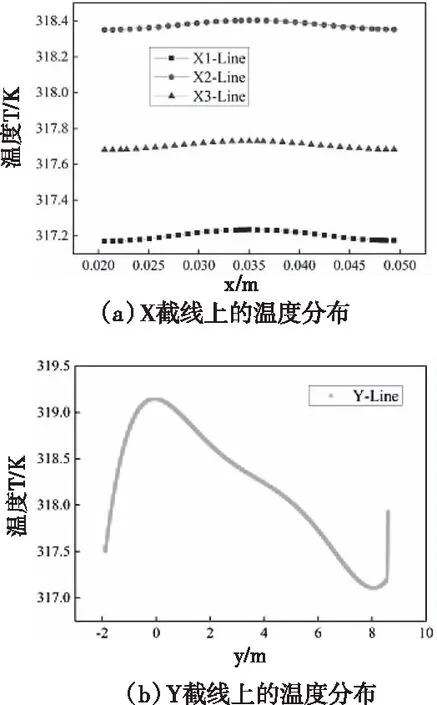
图7 X截线和Y截线上的温度分布

图8为沿流动方向不同截面上空气温度不均匀性变化与平均温度变化。从图8(a)可以看出，温度不均匀性在翅片段内先增大后减小，在出口延长段区域逐渐减小；从图8(b)中可以看出温度在翅片换热段内剧烈变化，在出口段基本不变。

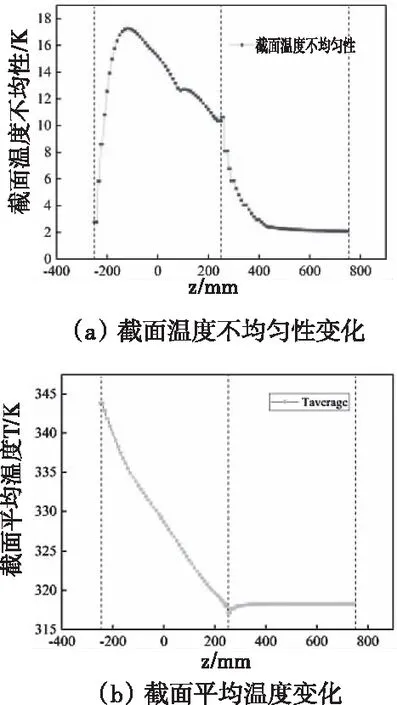
图8 流动方向不同截面温度不均匀性及截面温度变化

图9为各截面上平均压力、平均速度和平均湍流度的变化。从图9(a)中可以看出，压降主要发生在翅片通道段内，经过统计翅片段沿程压降为417.97Pa，出口延长段压力略有回升；从图9(b)可以看出出口段内速度变化很小；从图9(c)可以看出有两次增大的过程，这是由于进入和流出翅片通道造成的，之后平均湍流度迅速衰减，最终出口截面上的平均湍流度为2.93%。

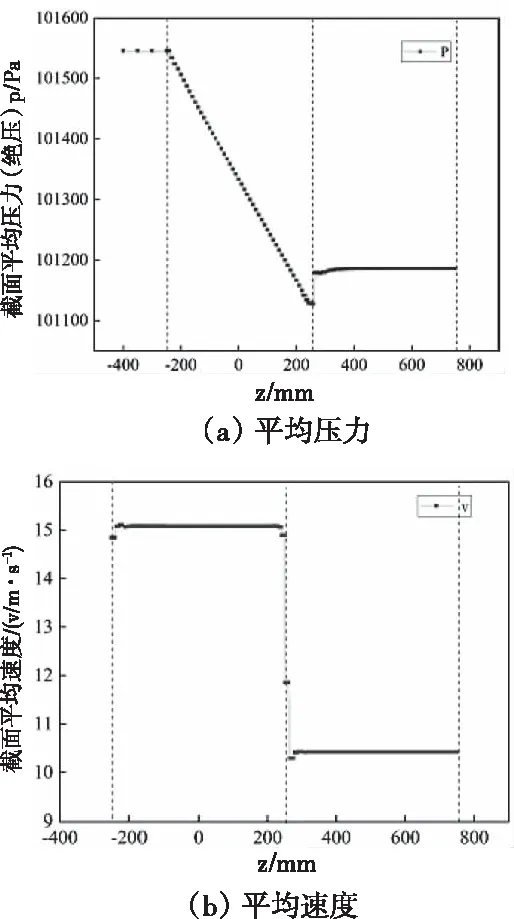
图9 流动方向不同截面平均压力、平均速度和平均湍流度的变化

图10为出口截面上Y截线上的速度和湍流度变化，从中可以看出速度和湍流度都只在靠近顶面和底面附近有急剧变化。图11为出口截面上X截线的速度和湍流度的变化，同样可以看出基本呈现左右对称的分布，且顶部(X1截线)和底部(X3截线)的速度较中间部分(X2截线)速度大，反之平均湍流度中间部分(X2截线)的数值较大。

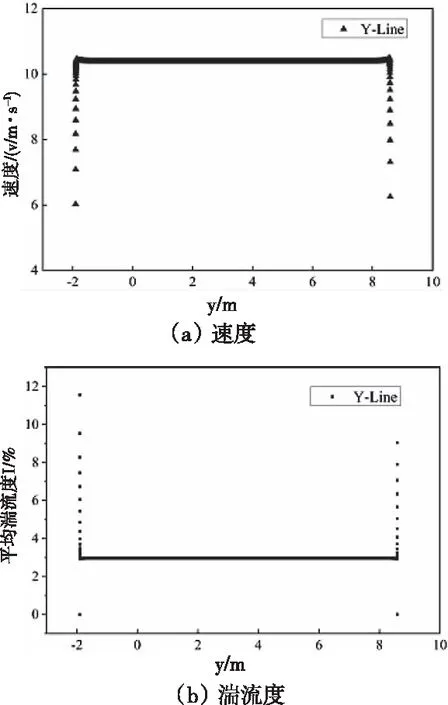
图10 出口截面Y截线上速度和湍流度分布

图11 出口截面X截线上速度和湍流度分布

MUSE 软件是国际上通用的板翅式热交换器设计软件[16,17]，可以进行板翅式换热器的设计和校核。采用MUSE软件对该超大型板翅式换热器进行计算，得到的出口截面温度不均匀性为1.26K与数值模拟的出口截面温度不均匀性2.07K比较接近，能满足该超大型板翅式换热器的设计和使用要求(出口截面温度不均匀性小于等于3K)。

5 结语

本文对一个超大型板翅式热交换器的典型换热结构(两层空气翅片结构)进行了数值模拟，采用了基于传热校核计算的温度分布函数边界条件，研究了出口段温度场不均匀性和平均湍流度变化。结果表明，出口段内温度不均匀性和平均湍流度沿流动方向逐渐减小，出口截面上的温度不均性为2.07K，平均湍流度为2.93%，数值模拟的结果与MUSE 计算值接近，能满足工程设计的需求。