基于达朗贝尔原理的车桥耦合振动模型仿真

2022-08-22刘宏伟沈世鑫

计算机仿真 2022年7期

刘宏伟，沈世鑫

(青海民族大学土木与交通工程学院，青海西宁 810007)

1 引言

达朗贝尔原理表明，对于任意一个物理系统来讲，其内部惯性力或是施加的外力，经过符合约束条件的虚位移处理，力所做的虚功数值之和为零[1]。根据该原理可知，在一个结构完整的动力系统内部，约束力做的虚功能够产生自动抵消过程，系统内其它力并不会受到约束力做功的影响。车桥能够将悬架与车架相连，车桥能够承载汽车的整体载荷，保证汽车在道路上的行驶安全。根据驱动方式的不同，可将车桥种类划分为转向桥、驱动桥、转向驱动桥以及支持桥等四个种类，不同种类的车桥有着不同的驱动功能。耦合处理能够将车桥与车辆其它部分建立起连接，形成一个缝隙整体，保证桥体的稳定。

最早对车桥耦合振动的研究从上个世纪初开始，以车辆和桥梁的实测数据为基础，在计算机技术的参与下逐渐仿真出实际的振动模型。近年来，相关学者也对车桥耦合振动模型做出了分析。文献[2]提出基于车桥耦合振动信号的桥梁结构损伤识别方法，以简支梁桥为研究对象，将桥梁的强迫振动响应作为扩展卡尔曼滤波算法的观测值，通过迭代更新完成桥梁结构损伤参数修正，据此构建桥梁耦合振动模型，完成结构损伤识别。该方法对桥梁损伤的识别较为准确，但计算过程较为繁琐；文献[3]提出基于路面激励空间效应的车桥耦合振动模型，通过虚拟激励方法构建车桥耦合随机振动模型，并分析了相干效应、时滞效应对车桥振动的的影响。该方法的分析结果较为准确，但对车桥耦合振动频率的控制效果较差。

针对上述方法存在的问题，本文在达朗贝尔原理下，仿真车桥耦合振动模型，并设计仿真验证所设计模型的有效性。

2 基于达朗贝尔原理的车桥耦合振动模型仿真

2.1 构建车桥振动响应关系

车桥耦合产生振动过程中，车辆的荷载与桥梁在形成一个时-空分布，在利用构建车桥振动响应关系时，首先构建车辆荷载时-空分布识别框架。采集车辆荷载的动态地形监测数据和车辆空间监控数据后，运用计算机视觉方法标记车辆的荷载信息[4]，结合交通设备的位置信息，划定两个车辆荷载目标区域。在区域1的动态地秤处安置一个探测区域，在区域2内选取车辆子图，利用子图识别和粒子滤波方法处理车辆经过全桥时的时-空位置信息[5]，构成如图1所示的时-空识别框架。

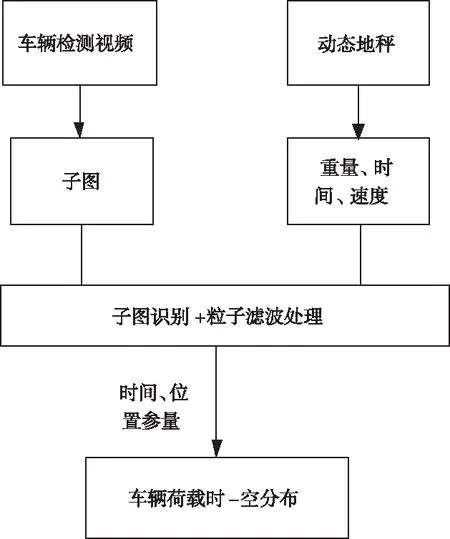
图1 构建的车辆荷载时-空识别框架

在图1所示的识别框架内，采用灰度背景减除法探测车辆的运行过程，将承载车辆的彩色帧图像处理为三个颜色通道，根据颜色通道表现出的强度值，采用达朗贝尔原理转化为处理灰度化数值，处理过程可表示为

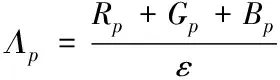
(1)

其中，Rp，Gp，Bp分别表示颜色通道的强度值，p表示车辆处理图像，ε表示达朗贝尔参数，Λp表示转换得到的灰度数值。灰度化处理后，根据车桥间的行驶图像，构建以行驶速度与车辆荷载重量为标准的指示图像[6]，根据计算机视觉方法体现出的桥梁接触点的竖向挠度和桥面的不平整度数值，计算车辆在桥面上的耦合位移，计算公式为

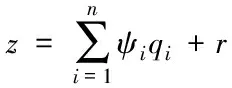
(2)

其中，z表示耦合位移数值，ψi表示接触点i的自由度，qi表示车辆与接触点间的面积，r表示桥面不平等参数。在上述耦合位移控制下，车桥之间形成一个耦合作用力，根据桥梁的各项参数，构建桥梁与行驶车辆作用力间的关系如式(3)所示

{Fv}=[c]{z}+[k]{z}

(3)

其中，c表示车辆的振动状态，k表示桥梁的振动状态，Fv表示桥梁与车辆之间的作用力。结合上述作用力关系，计算得到每个车轮在桥面上形成的荷载数值，可表示为

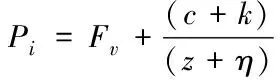
(4)

其中，η表示车辆与行驶车辆间的摩擦系数，其余参数含义不变。根据上述车桥间的耦合振动响应关系，建立车桥耦合振动模型。

2.2 利用达朗贝尔原理建立车桥耦合振动模型

在上述车桥耦合振动响应关系控制下，假定车辆与桥面始终保持接触[7]，设定行驶车辆模型由车轮质量和载体弹簧质量组成，在桥梁平衡状态下，构建如下图所示的车桥耦合模型：

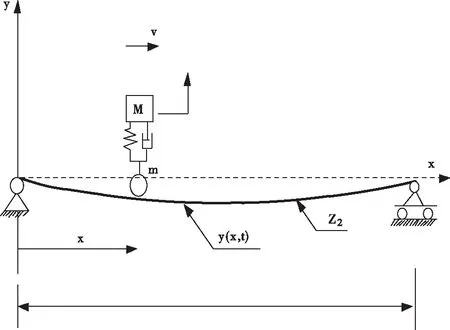
图2 模拟得到的车桥耦合模型

在如图2所示的耦合模型下，根据达朗贝尔原理构建图2耦合振动模型的方程

mz+c[z1-y(x，t)]+k[z2-y(x，t)]=0

(5)

其中，m表示车轮质量和载体弹簧质量总和，z1表示车轮产生的耦合位移，z2表示弹簧产生的耦合位移，y(x，t)表示桥梁产生的梁位挠度函数，其余参数含义不变。在上述振动方程控制下，使用计算式(2)得到的车轮与桥梁间的位移，划定耦合振动模型为不同节点，在不同跨径长度桥支梁的影响下[8]，模拟移动载体弹簧产生的耦合位移可表示为

x=vtk-xk

(6)

其中，v表示移动载体弹簧，tk表示车载时间，xk表示弹簧产生的耦合数值。在上述计算公式的控制下，不同的位移数值产生的弹簧耦合数值变化如图3所示。

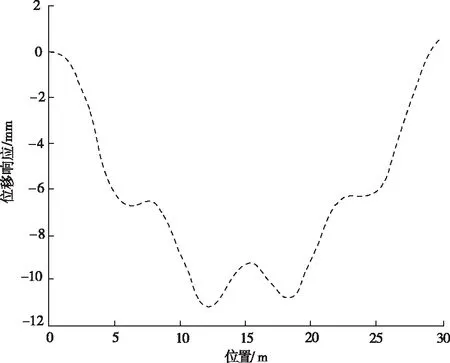
图3 弹簧耦合数值响应变化

在图3所示的响应变化下，选取位置响应最小的点作为模型构建点，根据上述计算式(3)中的荷载数值，在桥面接触间设定一个插值函数NT，整合为一个模态正交分解式的耦合振动方程，可表示为

(7)

其中，M表示车桥耦合振动模型中的广义坐标向量，C表示车辆的位移向量，u表示自由度，K表示模型节点，F1，F2分别表示车桥间的荷载力。为了消除桥面不平顺产生的随机荷载影响，设定一个桥面不平顺随机过程，提取慢变调制函数，在模型空间内的空间域转化为时间域[9]，采用脉冲函数处理上述计算式(7)，将处理后的振动模型作为最终的振动模型。以得到的振动模型为作用对象，仿真处理车桥耦合振动模型。

2.3 完成车桥耦合振动模型的仿真

仿真处理车桥耦合振动模型时，以上述处理得到的节点作为处理对象，将耦合振动响应过程转化到模型阶段上，转化过程可表示为：

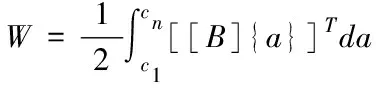
(8)

其中，W表示转化参数，c1～cn均表示车桥间主振动与内振动联合参数，B表示耦合振动模型，{a}表示激励集合，T表示转化周期。转化处理后，根据耦合振动模型振动单元功能[10]，仿真模拟车辆平动动能和转化动能，可表示为

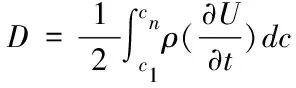
(9)

其中，ρ表示振动线密度，U表示振动惯量参数，其余参数含义不变。在平动动能和转化动能的控制下，构建的耦合振动模型侧向加速度峰值较大，一旦扭振频率与侧向模态频率接近，车桥之间就会产生共振，破坏已构建振动模型的牢固性[11]。计算耦合振动模型在共振时产生的动态变化量

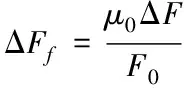
(10)

其中，ΔF表示侧向加速度产生的弹性力，μ0表示车桥间的刚度系数，F0表示桥梁轧制力的稳态值。平稳处理上述动态变化量后，为了减少仿真过程中所需的计算量，整合上述处理过程为一个振型函数，可表示为

(11)

其中，L表示桥梁的长度，m表示车桥质量，x表示耦合振动位移，n表示车辆加速度峰值。形成的仿真过程如图4所示。

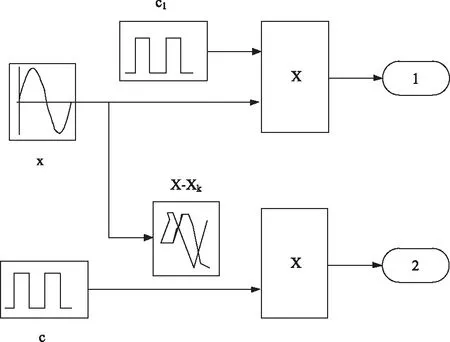
图4 耦合振动模型的仿真过程

不断更新车辆加速度中的峰值后[12]，最终完成对基于达朗贝尔原理的车桥耦合振动模型的仿真过程研究。

3 实验分析

3.1 实验准备

利用结构加载系统来模拟车辆在桥梁上形成的加载力，使用温度量程在100～600℃的温度控制系统，在计算机内安装一个数据采集软件后，连接一个最大荷载值为1000kN的计算机控制电子万能实验机，设定实验机的加载控制精度为1%，采用测量标距为45mm、量程在0～30mm、精度为0.01mm的电子引伸计，搭建实验环境结构如5图所示。

图5 搭建的实验环境

在图5所示实验环境下，采用低合金高强度钢作为桥梁制作材料，设定模拟桥梁厚度为30mm，标距长度为1m，平行段的长度为1.2m，控制各个桥梁间连接处的误差数值小于0.05mm后，调试实验环境中的设备，将制作的模拟桥梁构建放置在实验机上，保持桥梁构件处于垂直方向，使用温度加载装置加载模拟构件后，在计算机数据采集软件中输入试验车的参数，输入参数如表1所示。

表1 实验车辆参数

以表1所示的各项参数作为车辆在桥梁上形成的固定参数，当计算机内结构加载软件各项数值显示正常时，分别使用文献[2]方法、文献[3]中的仿真方法以及文中设计的仿真方法进行实验，对比三种仿真方法的性能。

3.2 结果及分析

基于上述实验准备，调用计算机程序对仿真结果进行对比验证，以车桥处的横向位移作为处理对象，以实验车辆参数作为标准位移参数，设定仿真时间为200s，以20s作为一个时间统计点，以表1设定的各项数值作为参考，运用计算式(2)计算得到位移数值，并将其作为标准车桥位移，统计车桥耦合过程中产生的误差，误差结果如表2所示。

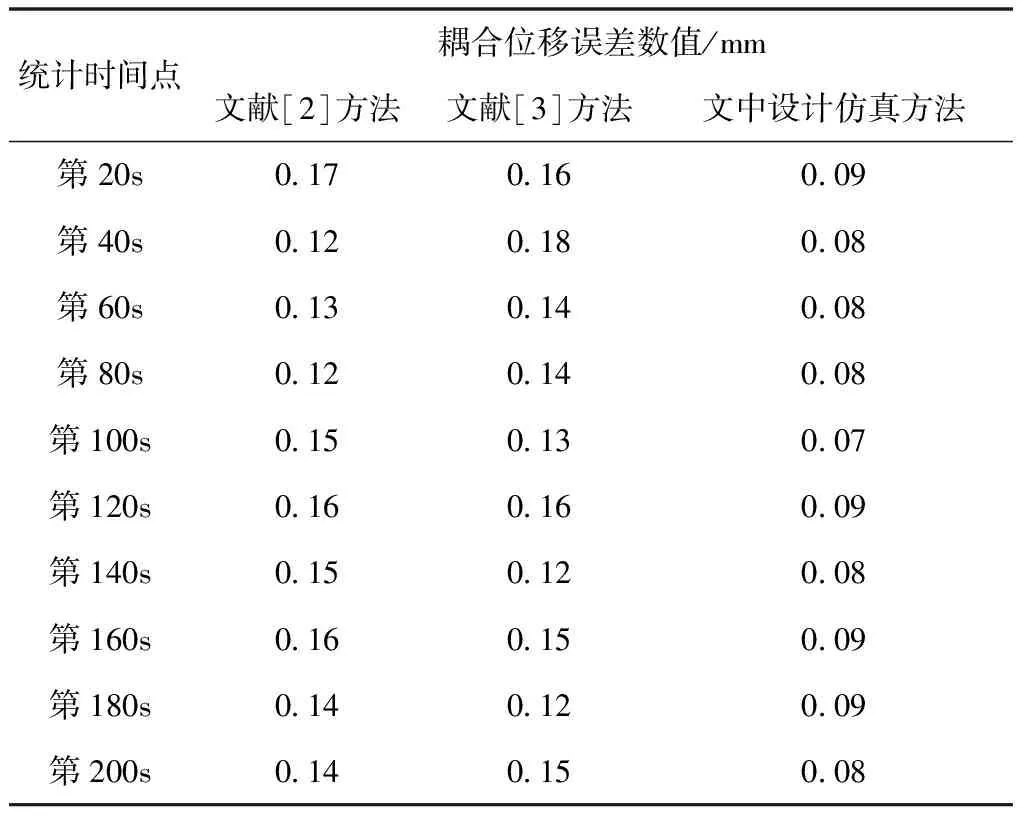
表2 三种仿真方法得到的耦合位移误差

由表2所示的各项位移误差数值结果可知，在相同的时间统计点下，文献[2]方法产生的平均位移误差数值在0.144mm左右，耦合位移误差数值较小，文献[3]中产生的平均位移误差数值在0.145mm左右，耦合位移误差数值最大，而文中设计的仿真方法实际产生的耦合位移误差最小，数值在0.083mm之间。

在上述实验环境下，采用傅里叶变换处理上述得到的耦合位移后，将统计时间点处理为五阶振动频率，采用有限元程序Bmode处理这五阶振动频率，得到的参数数值结果如表3所示。

表3 三种仿真方法产生的振动频率数值

由表3所示的振动频率数值变化可知，以相同的阶段横向作为对比指标，在三种仿真方法的控制下，文献[3]方法得到的耦合振动频率最大，文献[2]方法方法得到的耦合振动较小，而所设计方法的耦合振动频率最小。由此可见，所设计方法对振动频率的控制效果较好，能够在一定程度上抑制车桥之间共振作用对桥梁结构产生的冲击。

设定三种仿真方法的操作数据数量为10组，定义仿真方法的训练参数R为表示仿真方法计算量的参数，训练参数R的计算公式可表示为

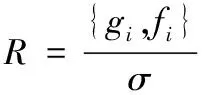
(12)

其中，σ表示各项数值的高斯算子再生核，gi表示车桥的各项数据集合，fi表示精度参数。计算并统计三种仿真控制下，仿真车桥耦合振动模型的训练参数大小，结果如表4所示。

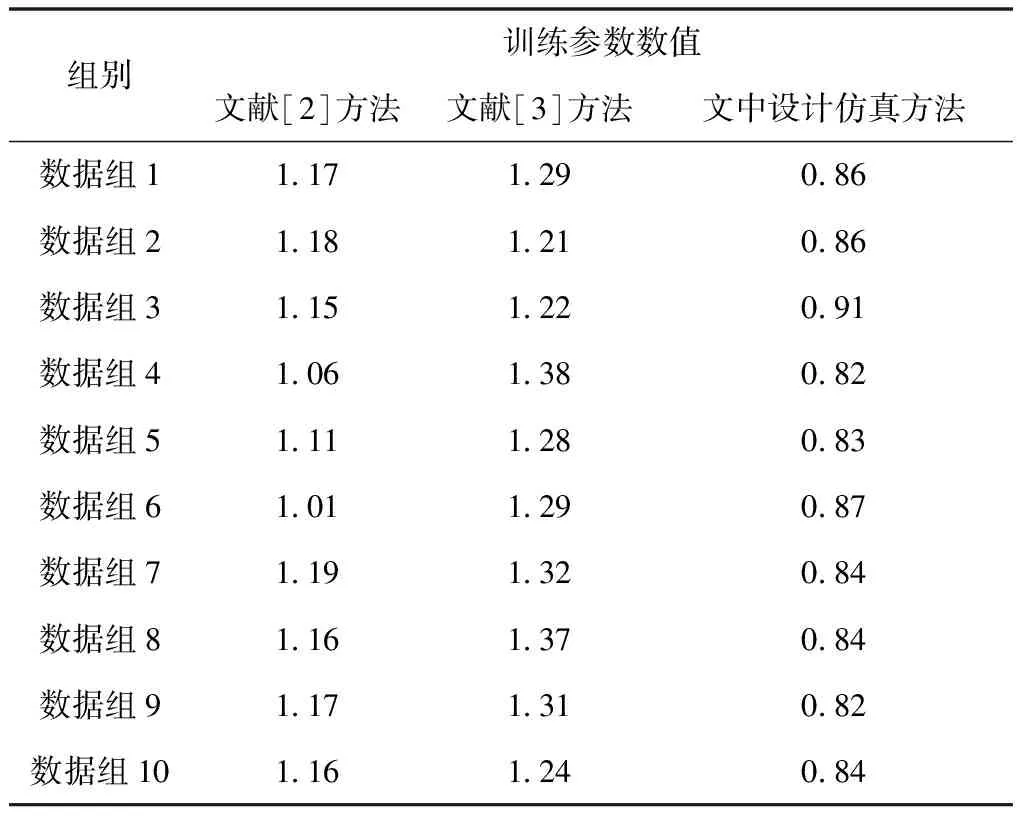
表4 三种仿真方法得到的训练参数数值

定义训练参数R数值大于1表明该种仿真方法产生较大的计算量，R的数值小于1时，表明该种仿真方法计算量较少。由上表所示的训练参数数值结果可知，文献[2]方法与文献[3]方法产生的训练参数数值大于1，表明两种仿真方法产生的计算量较大，而文中设计的仿真方法得到的训练参数数值小于1，表明该种仿真方法最终产生的计算量最少。