基于相似日PSO-SVM的机场流量预测
2022-08-22王兴隆石宗北
王兴隆,石宗北,贺 敏
(中国民航大学空中交通管理学院,天津 300300)
1 引言
随着我国民航业的飞速发展,航班量与日俱增。在有限的机场容量以及管制员配置的情况下,进行航班流量的有效预测将对机场动态容量评估、保障航班正常性以及辅助管制决策等均有很重要的意义。
进离港的航班流量往往受地面保障、天气、空域情况等多种因素影响,因而较难对航班流量进行准确预测。相似日作为一种基于历史数据的方法,有较好的表现效果,相似日预测在工业以及实际生产生活中有着广泛的应用。基于相似日的衍生预测模型也在许多行业有着较好的实现效果。莫维仁[1]等最早提出了数据波动产生的趋势相似日以及形状相似日的概念并基于相似日对短期负荷模型预测进行了探讨;牛东晓[2]等提出相似日聚类方法并通过自适应权重组合预测模型对电力系统负荷进行预测;陈昕、唐湘璐[3]等采用相似日聚类与时间段划分的二步聚类过程,对温室中温度的调控进行了预测,在农业生产中取得了较好的效果;张平,潘学萍[4]等通过将相似日数据序列进行离散化小波变换,结合神经网络模型实现了短期负荷预测。在民用航空领域,Sreeta Gaorripaty等人以纽约肯尼迪机场(JFK)及新泽西纽瓦克机场(EWR)为例进行了相似日选择的研究,验证了相似日方法在民用航空中的可行性[5]; Shon Grabbe和Banavar Sridhar从气象角度对机场的相似日进行了研究,对于2011年的所有美国机场进行聚类,得到在不同气象条件下机场实施的地面等待程序(GDP)的集划分[6]。
然而相似日聚类方法同时间序列分析、分形理论等民航运输领域常用的流量预测方法一样[7-8],其得到的结果源于对系统本身的合理外推,缺乏对不确定影响因素的考虑。神经网络虽然可以很好地刻画非线性关系,但存在网络结构难以确定、过拟合、局部极值等问题,难以保证预测精度[9]。支持向量机(SVM)通过最小化结构风险同时解决了以上存在的问题。
基于以上情况,利用相似日方法善于对历史运行模态进行挖掘的特点及SVM预测精度表现良好的特性建立机场相似日聚类支持向量机回归模型。同时,通过粒子群算法进行参数寻优,以达到实现航班流量准确预测的目的。
2 相似日聚类
知识挖掘可以从大规模的数据库和历史信息中挖掘提取隐含、不确定的变化信息,具有广泛的应用价值[10]。因此,从历史数据寻找相似日,利用相似日信息与航班流量之间的映射关系,推测待预测日的航班流量情况。通过知识挖掘确定相似日常用的方法有模式识别、聚类方法和相关性分析等。
对一给定样本集合A,有:tij∈A,i∈[1,2,…,n],i∈[1,2,…,m]。其中i为A中的样本个数;j为样本的特征。对于样本集中的每个样本,均可由m个特征描述。即对于特征集B有:ti=[ti1,ti2,…,tim]。因此,衡量相似日的样本数据可由n*m维矩阵表示。即
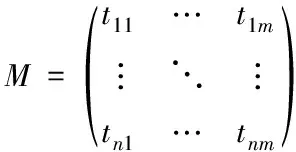
(1)
基于历史统计数据,根据民航情报服务中心发布的气象数据进行相似日粗选,选择与目标机场气象条件相似的日期,然后提取粗选集中相似日的特征向量对机场进行灰色聚类。过程如下:
1) 基于气象信息的相似日数据粗选
首先从影响机场本场运行的气象条件的角度进行相似日粗选以达到对数据集进行清理的效果。由民航情报服务中心发布的通告可知天气现象对机场运行造成的影响可分为雷雨、对流、低能见度、降雪、大雾等,因此可以根据历史数据中的不同天气类型先筛选出部分数据作为粗选样本集。
2) 历史数据处理
对于同一样本数据中的不同指标,各自指标代表着不同的物理含义,而且数据分布区间不均,为了保证后续训练效果的精确度与准确性,需要对粗选集中的数据进行进一步处理。无量纲化可以抵消指标间不同物理意义带来的影响。无量纲化方法如下
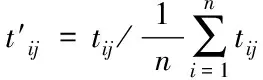
(2)
3)历史数据聚类
比对待预测日与历史运行日的关联度,对机场的运行历史数据进行分类。本文选取衡量机场运行状态的信息包括通行保障能力C、当日计划航班总数P、单位小时最大航班量R、风速W、能见度V等5类。其中,通行保障能力数据来源于民航情报服务中心发出的机场运行通告,计划航班数、及高峰小时航班数数据来源于飞常准业内版,气象数据采自METAR报报文。因此任意一天θ的机场运行数据可以表示为由五种指标构成的行向量,即
tθ=[tθC,tθP,tθR,tθW,tθV]
(3)
对于待预测日,其第j个特征(j∈[1,2,3,4,5])与所选取的历史运行日θ之间有如下关系:
σθ(j)
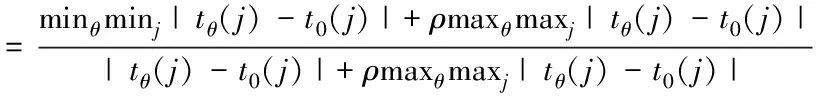
(4)
其中,σθ(j)为待测日第j个特征与历史相似日的关联系数;ρ是分辨系数,一般取0.5;t0(j)是代表待预测日的第j个特征。
计算历史相似日θ与待测日特征向量的关联度γθ。
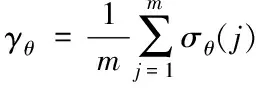
(5)
根据筛选并处理过的相似日特征集逐一与待预测日的运行条件进行比较并计算二者的关联度。将关联系数较高的数据作为新的样本集。
3 粒子群优化的支持向量回归模型(PSO-SVM)
3.1 支持向量机原理
支持向量机(SVM)具有在小样本下仍有较好的学习效果的优点。在通过引入核函数将样本数据映射到高维空间后可以进行非线性化处理,作为一种泛化能力较好[11]的有监督的学习算法被广泛使用。
对于筛选出的训练样本集{(x1,y1),(x2,y2),…,(xk,yk)},t为样本总数,其中xk为k维空间Rk中的输入向量;yt是输出值。引入回归函数f(x)=ω·φ(x)+b。其中,ω为权重向量,且有ω∈Rk。φ(x)为可以将原数据映射到高维空间的核函数。SVM作为一种监督学习方法对数据进行预测的根本思想是在决策集空间F中寻找一种决策使损失函数期望最小化。
Rexp(f)=EP[L(Y-f(X))]
(6)
其中,L是用于表征预测值与实值之间差异的损失函数。Rexp的引入表表征了支持向量机模于数据分布P(X,Y)平均意义下的损失,但由于P(X,Y)未知,为了解决这个问题引入结构化风险函数Rsrm。
Rsrm≤Remp+λJ(f)
(7)
其中,Remp为经验风险函数,J(f)为决策空间上表征模型复杂度的泛函。由Rsrm最小化,回归函数最小化等价于求解有约束的代价泛函如式(8)示。
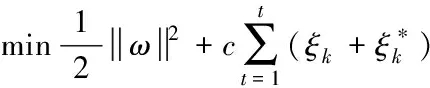
(8)
其约束条件满足如下条件
ω·φ(x)+b-yt≤ξk+L
(9)
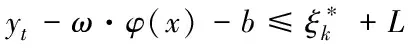
(10)

3.2 粒子群优化模型
粒子群优化(Particle Swarm Optimization,PSO)算法是通一种基于群体智能的全局随机搜索算法[12]。它的基本核心是利用群体中的个体对信息的共享从而使得整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的最优解,每个优化问题的解称之为“粒子”。粒子群算法通过不断移动的粒子来进行迭代寻优,粒子具有两个属性:速度和位置,速度代表移动的快慢,位置代表移动的方向。将粒子位置信息代入适应度函数,得到适应度值。在寻优过程中,粒子通过自己的个体极值pbest和群体极值gbest来更新速度和位置[13]。
D维空间内第u个粒子的位置和速度向量表示如下:
Xu={xu1,xu2,…,xuD}
(11)
首个粒子在D维空间的速度向量表示为:
Vu={vu1,vu2,…,vuD}
(12)
第一个粒子到目前为止搜索的最佳位置为:
Pbest={pbest1,pbest2,…,pbestD}
(13)
整个粒子群搜索到的最优位置为:
Gbest={gbest1,gbest2,…,gbestD}
(14)
在迭代过程中,粒子的速度与位置由下式确定
vα,β(s+1)=ωvα,β(s)+c1r1(pbestα,β(s)-xα,β(s))
+c2r2(pbestα,β(s)-xα,β(s))
(15)
xα,β(s+1)=xα,β+vα,β(s+1),
α=1,2,…,N,β=1,2,…,n
(16)
其中,s是迭代次数;N为粒子个数;c1和c2分别为粒子的认知系数与社会学习系数;r1和r2为[1,2]之间的随机数;惯性权重ω为一个定值。
在支持向量机回归模型中,参数的选择对预测结果有着很大的影响,利用粒子群快速全局优化的特点对SVM的参数进行优化可以提高预测精度的同时并减少试算的盲目性。本文选取SVM预测结果的均方误差(MSE)作为粒子群的适应度函数。针对惩罚系数c和核函数参数g进行优化,即搜索空间D=2。
4 机场流量预测流程
结合上文所提相似日聚类及PSO-SVM预测模型,实现机场流量预测。基于机场相似日的PSO-SVM预测流程如图1所示。
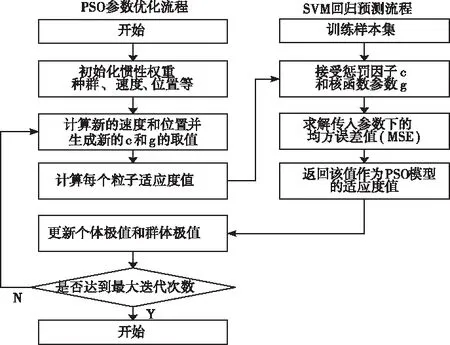
图1 PSO-SVM机场流量预测流程图
1)通过灰色聚类对机场的历史运行情况进行相似日筛选,得到相似日数据集。
通过对目标机场在不同天气下的运行情况进行历史数据统计,采用通行保障能力、计划航班数、单位小时最大航班量、风速、能见度等信息进行组合,构建相似度矩阵建立机场相似日灰色聚类模型,选取与待预测日关联度较高的数据构建样本集。
2)将筛选出的相似日数据集作为样本集,并对样本集进行归一化处理。对样本集进行划分,其中将25%作为测试集,75%作为训练集构建支持向量回归模型。
3)通过粒子群算法对支持向量回归模型中的惩罚系数c及核函数参数g进行寻优。
以支持向量机中的惩罚系数c和核函数半径g的取值作为粒子,设置迭代次数,初始化粒子群P,随机初始化粒子位置和速度,并按式(15)和式(16)更新速度和位置,生成新的c和g的值,得到此时支持向量机中的均方误差MSE作为每个粒子的适应度值。对每个粒子,比较它的适应度值和它经历过的最好位置的适应度值pbest,如果更好,更新pbest;储存个体极值pbest和群体极值gbest。直至达到迭代次数停止,输出最优适应度值和此时的c与g的值。粒子群优化支持向量机参数的流程如图2示。
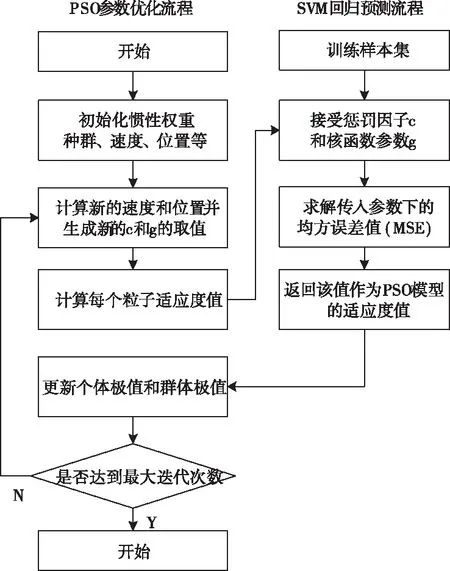
图2 PSO-SVM算法流程
设定惯性权值ω=0.9,学习因子c1=1.6,c2=1.2,种群粒子数n=50,最大迭代次数N=100,c和g的速度边界设定为[0.001,10]。
4) 用经过PSO算法寻优的SVM模型对机场待预测日的运行情况进行预测,获得待预测日的机场流量情况。
5 算例验证
基于2018年全年的民航情报服务中心的气象通告结合飞常准平台的机场准点率数据对2018年广州白云机场的进离港航班情况进行研究,以验证本预测模型的可靠性。以雷雨天气情况下的运行情况为例,对2018 年9月7日雷雨天气运行情况下广州白云机场机场每小时服务航班的航班流量进行预测。
以2018年8月为例,将机场运行数据结合民航情报服务中心发布的气象通告以及当日运行的METAR报进行相似日筛选,得到信息如表1所示。
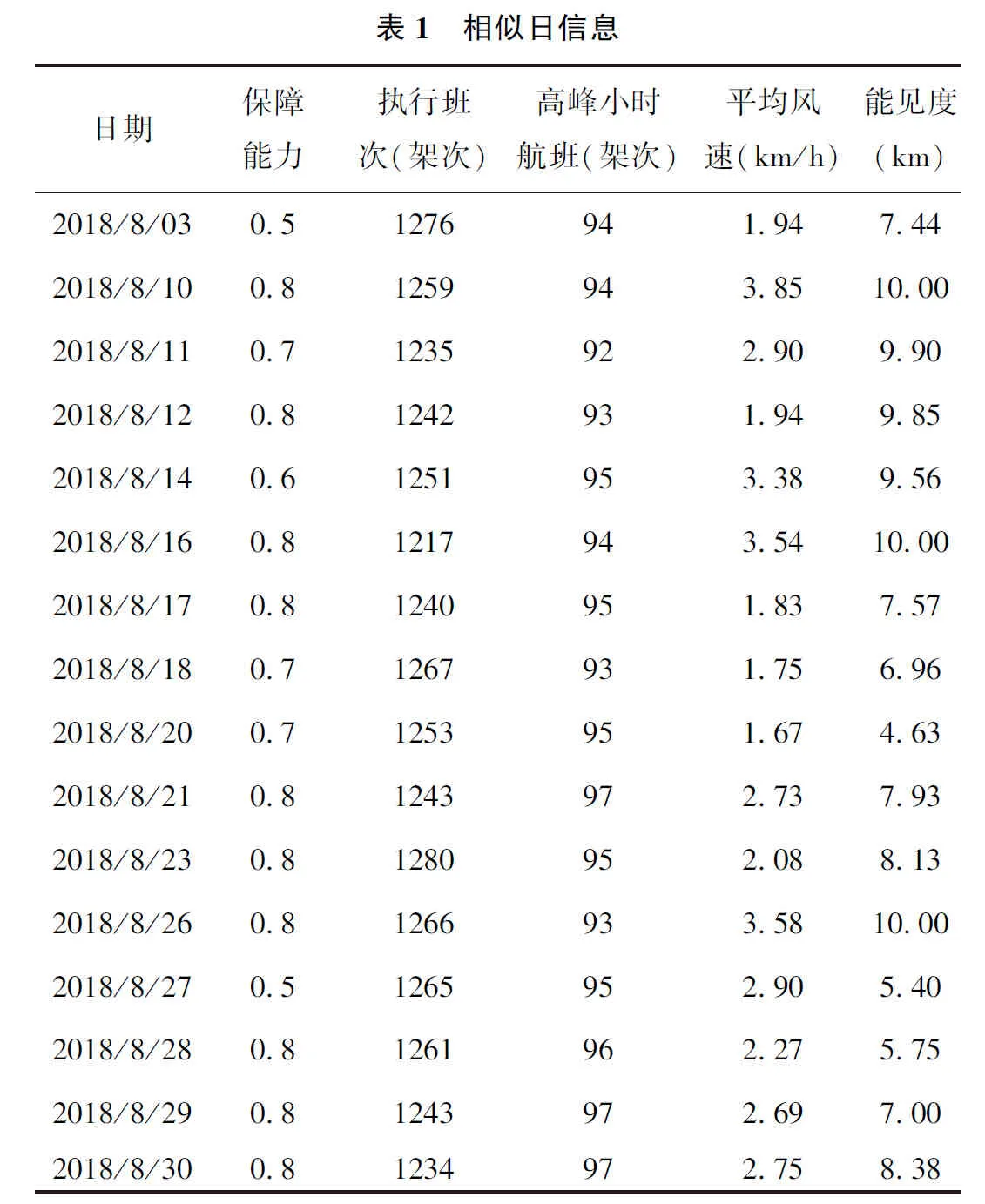
首先,对表1中的信息进行无量纲化处理得到灰色聚类数据样本;然后依据关联度公式对收集到的数据进行计算,选取相似度较高的日样本数据作为支持向量机模型的训练样本如表2所示。在本文中,以2018年9月7日为待预测日,因此选取计算后与待预测日关联度在0.85以上的7个运行单位日作为最终训练集。

表2 相似日关联度
将样本日数据以及待预测日的数据输入,用PSO算法训练SVM获得参数。其中,本文选取的核函数为多项式核函数,多项式次数d=3。由于夜间进离港航班数量较少不具有代表性,因此本文用参数寻优后的模型对白云机场2018年9月7日早06:00至晚23:00的航空器进离港情况进行预测,并与实际结果进行比较。适应度变化曲线如图3示。
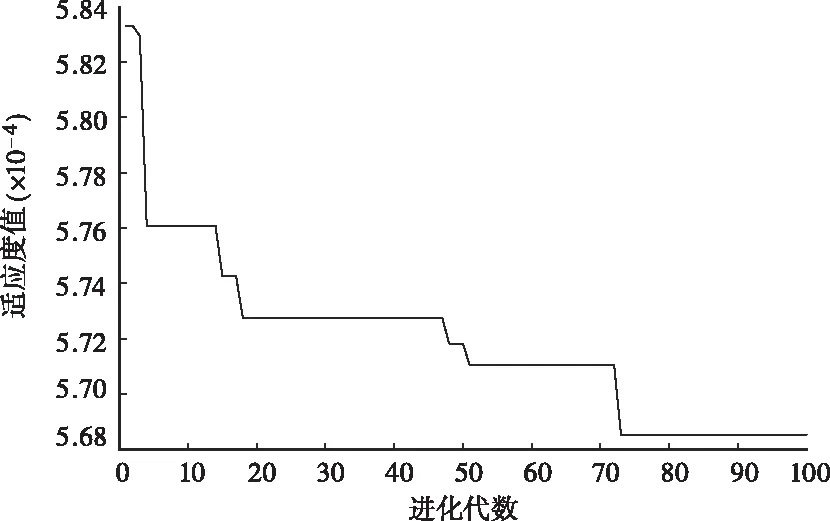
图3 适应度变化曲线
由图3可知,在46代左右算法快速收敛,在75代左右达到最优值。经多次迭代寻优后得到的惩罚系数c=3.44,g=0.17。在最优参数的基础上对待预测日航班流量进行预测,实际值与预测值的相对误差绝对值最大值7.14%,最小值为0,平均相对误差为3.26%,均方根差(RMSE)为6.61。
分别采用相似日-BP神经网络模型与不进行相似日处理的传统PSO-SVM模型数据进行比较。各算法预测值与实际值的比较结果如表4示。真实值与预测值的折线图如图4示。

表4 BP神经网络预测结果
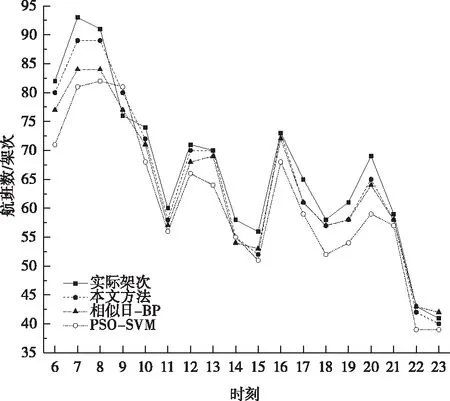
图4 预测结果对比图
在相似日-BP神经网络回归算法得到的预测结果中,相对误差绝对值最大值为9.68%,最小为0,平均相对误差为4.30%,均方根误差为3.82。而在未经相似日处理的PSO-SVM算法中,相对误差绝对值最大为14.49%,均方根误差为6.61。由表4可知本文所提方法有着较好的预测精度。相似日聚类粒子群优化的支持向量机模型对每小时实际服务的航班量预测具有较好的效果。
对广州白云机场进行航班量预测的基础上,本文进一步对我国两个千万级机场,上海浦东机场及成都双流机场进行了航班量预测。分别采用本文所提方法及相似日-BP网络和传统的PSO-SVM方法预测2018年7月27日上海浦东机场及2018年7月15日成都双流机场降雨条件下的运行情况。各预测方法在不同数据集上的均方根误差如图5所示。
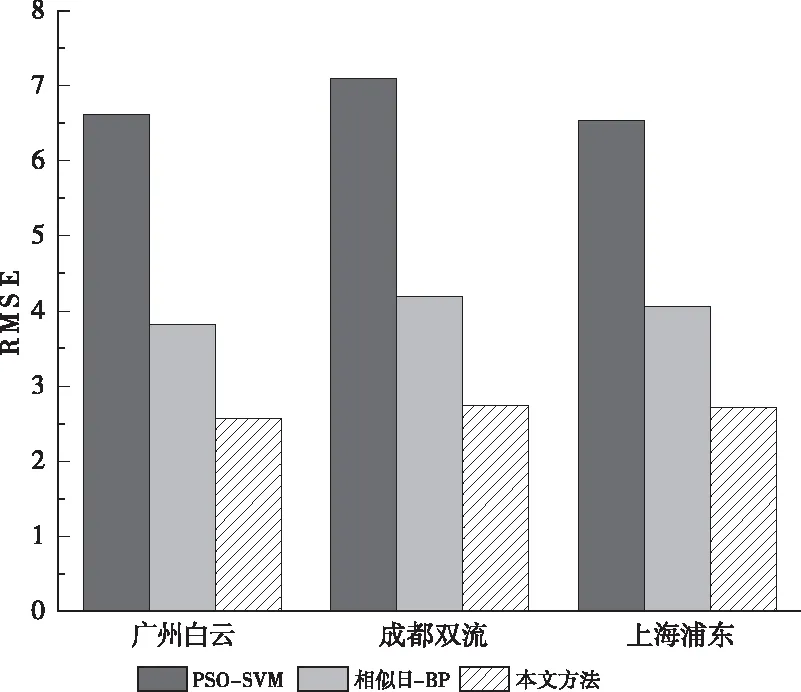
图5 算法误差对比
如图5所示,本文所提预测方法在不同数据集上均有较好表现,且对不同机场的预测误差波动范围较小,有着较好的稳定性。而未采用相似日处理的传统PSO-SVM方法有着较大的预测误差。
6 结论
通过相似日PSO-SVM的方法,对机场每小时航班量进行了预测。通过基于数据驱动的相似日选取方法,在大量历史数据中提取与待预测日关联度较高的运行单位日作为相似日,提取出的数据特征相似、适于进行预测;通过支持向量机对机场每小时航班量进行预测,对机场动态容量评估、管制员战术决策均具有较大的实际应用价值。最后应用广州机场的实际运行数据进行了分析,以2018年9月7日雷雨天气情况下的运行情况为例进行了航班流量预测,在相似日PSO-SVM模型中平均累计预测误差为3.40%。取得了较好的训练成果,证明了方法的可行性。
