中轨道Walker导航星座备份策略分析SS设计

王许煜，胡 敏，赵玉龙，李玖阳

(1. 航天工程大学研究生院，北京 101416；2. 中国人民解放军32024部队，北京 100094)

1 引言

导航星座运行过程中，卫星由于受到可靠性、维护操作以及太空环境的影响会发生长期、短期或维护故障[1]，从而导致星座服务性能下降。因此，需要根据星座实际状况采取相应的备份策略，以便在卫星发生故障时，尽可能在短时间内恢复星座的性能[2]。中轨道Walker导航星座备份策略分析仿真软件能评估不同备份策略对星座服务性能和运行成本的影响，可实现备份策略的最优化，对星座连续稳定的运行和星座管理者的管理决策有着重大的意义。

目前，对于星座备份策略仿真软件的研发已经取得了一定的成果。Jean-Franqois Ereau等人[3]采用软件MISS-RdP对星座建模和评估，利用Petri网描述星座备份的逻辑行为，并对输入参数进行敏感性分析，从而评估星座可用性和备份策略。GMA公司开发了ORION软件，其结合了数据库、优化程序和蒙特卡洛仿真，能分析星座每个阶段的最佳策略，该软件通过考虑卫星可靠性和星座服务可用性来评估备份策略[4-5]。G. Salgado等人[6]利用基于Petri网和蒙特卡洛仿真开发的软件计算星座可用性，该软件考虑星座确定事件和随机事件，提供瞬态和稳态的周期性结果，可用于分析星座的备份策略。Deimos航天公司开发了一款随机模拟软件，从服务性能、发射次数和所需卫星数等方面评估不同条件下的星座备份策略[7]。

本文以中轨道Walker导航星座为研究对象，开发了一套中轨道Walker导航星座备份策略分析仿真软件。目前该仿真软件已推出1.0版本，重点研究了卫星可靠性模型的建立，同时具备对不同备份策略进行分析评估的能力以及对备份策略中在轨备份星轨位优化设计的能力。本文阐述了该仿真软件的设计和实现，并给出了应用实例。

2 软件设计思路

软件的设计思想为：首先综合考虑卫星的随机故障和损耗故障，建立卫星可靠性模型，并将其作为星座模型的重要输入，然后利用蒙特卡洛方法评估不同备份策略对星座运行参数的影响，最后对在轨备份星轨位进行优化设计。其主要解决了以下三个方面的问题：

1)卫星可靠性模型的建立

现有软件大多采用简单的指数分布模型模拟卫星可靠性，而该模型假设卫星故障率为常数无法准确描述卫星早期故障和损耗累积的过程，本文通过分析卫星系统的动态逻辑关系建立动态故障树模型，然后对其分析得到卫星随机故障模型，并结合损耗故障建立卫星可靠性模型。

2)星座备份策略的分析评估

星座模型的建立面临着状态空间爆炸和资源分配等问题，而现有方法为了便于问题分析都对星座模型进行简化，同时对于备份策略的评估也多采用单一指标，这不利于备份策略的优化设计。本文利用随机时间Petri网(STPN，Stochastic Timed Petri Nets)的结构化分析优势对星座进行建模，并建立可用性和运行成本模型以评估备份策略。最后，通过比较不同的备份策略获得最优备份策略。

3)在轨备份星轨位的优化设计

现有软件大多只分析备份策略中的备份卫星数，而对于备份星轨位的设计则少有研究，本文考虑星座运行期间在轨备份星与工作卫星存在短时间内共同提供服务的情况，通过建立轨位优化模型，利用多目标算法对其进行仿真计算获取备份星优化轨位。

3 软件设计

3.1 框架结构

软件主要包括界面与仿真程序两大部分，界面用于输入参数，仿真结果以仿真图和数据文件的形式输出。采用模块化的设计原则，将软件分成独立的功能模块，各模块之间通过输出结果进行连接，从而形成链式的软件结构，总体框架如图1所示。

图1 中轨道Walker导航星座备份策略分析仿真软件总体框架

软件以 Windows 系统为操作平台，采用Matlab编程语言设计开发软件系统架构，仿真程序及软件界面，预先留好输入和输出接口，从而使软件具有高度的开放性和通用性，易于编写、修改、使用和二次开发[8]。

3.2 功能模块设计

3.2.1 卫星可靠性分析模块

卫星可靠性分析模块根据输入的底事件失效率参数对卫星可靠性进行仿真计算。其相关技术包括：动态故障树建模、动态故障树分析、卫星可靠性模型建立。

3.2.1.1 动态故障树建模

根据卫星在轨故障统计结果显示，卫星中电源、姿轨控和推进3个分系统在轨故障所占比例最高[9]。因此，重点分析这三个分系统进而建立卫星的动态故障树模型。图2为卫星的简要故障树。

图2 卫星简要故障树

3.2.1.2 动态故障树分析

采用马尔可夫链和二元决策图相结合的方法对动态故障树进行分析得到卫星的随机故障模型，该方法结合了传统故障树分析方法和马尔可夫链的优点，能实现对动态系统的可靠性和安全性分析[10]。

具体过程包括：首先利用线性搜索算法对动态故障树进行模块化分解，得到动态子树和静态子树。然后利用二元决策图对静态子树进行求解,而动态子树则转化成马尔可夫链进行求解[11]。最后依据各子树求得的故障概率获得顶事件的发生概率，并结合其它分系统的失效率，进一步得到卫星的随机故障模型。

3.2.1.3 卫星可靠性模型建立

考虑卫星的损耗故障，利用正态分布模型模拟卫星损耗故障[12]，并将其与随机故障模型相乘得到卫星的可靠性模型

(1)

式中：R(t)随机故障为随机故障模型可靠性，μ为均值，σ为标准差，t为卫星的工作时间。

3.2.2 星座备份策略分析评估模块

星座备份策略分析评估模块主要包括以下四项内容：建立导航星座STPN模型、建立可用性模型、建立运行成本模型、仿真评估不同备份策略。

3.2.2.1 导航星座STPN模型

中轨道Walker导航星座由24颗卫星组成，星座参数为24/3/1，轨道高度为21528km，倾角为55°。考虑在轨和地面备份两种策略，利用库所表示系统状态，变迁表示系统事件，构建单星、轨道面STPN模型，进而建立星座STPN模型，该模型模拟了星座确定因素和随机因素，包括卫星故障、故障修复、替换卫星以及地面生产和发射卫星等过程，能详细描述星座运行的逻辑结构特性以及备份过程。

3.2.2.2 星座可用性模型

为了便于星座可用性的评估，根据星座中故障卫星数对星座进行状态等级的划分：

1)P1：星座中无故障卫星；

2)P2：星座中有1颗故障卫星；

3)P3：星座中有2颗故障卫星；

4)P4：星座中有3颗故障卫星；

5)P5：星座中故障卫星数大于3颗；

选取星座CV值(Constellation Value)作为评估不同星座状态性能的指标[13]，该值能衡量星座在服务区内的覆盖性能，其定义如下

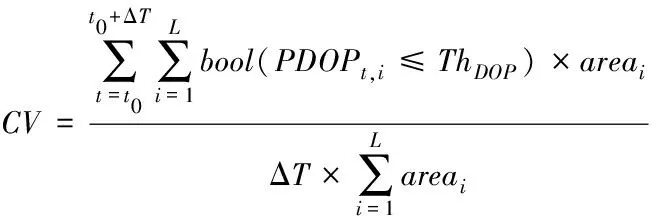
(2)

式中，t0为初始时刻，ΔT为仿真时间，PDOPt，i为t时刻第i个网格的PDOP值，ThDOP为精度因子阈值，bool()为布尔函数，L为网格总数，areai为第i个网格的面积。

由于在同轨道面上出现三颗或更多卫星发生故障的概率较低[14]，且星座中出现多颗卫星故障的概率也很小，因此只计算P1、P2、P3以及P4状态下的星座CV值，如表1所示。

表1 不同状态下的导航星座CV值

之后结合星座状态概率和星座CV值提出星座平均服务可用性的计算公式，其中星座状态概率为星座处于不同状态等级的时间占运行时间的比例，具体计算公式如下

(3)

式中，k为星座状态的第k种，N为星座状态总数，Pk为星座处于第k种状态的发生概率，CVk为星座处于第k种状态下的星座CV值。

根据导航星座服务可用性标准，对可用性指标提出设计要求：导航星座在全球区域内PDOP≤4的平均服务可用性≥95%[15]。由于P1、P2、P3状态的星座CV值≥99%，因此将其统称为S1状态，同时将S1或P4状态称为S2状态，并根据各状态的CV值提出备份策略的最低要求：星座达到S2状态的概率优于95%，星座达到S1状态的概率优于93%。

3.2.2.3 星座运行成本模型

星座成本模型包括：固有成本、补给成本、储存成本和短缺成本。固有成本是指星座组网阶段的成本。补给成本是指星座补网的成本。储存成本是指库存储存备份星的成本。短缺成本是指故障卫星未能及时替换而造成的经济成本。星座运行成本模型如下所示

(4)

式中：Q为固有成本，R为补给成本，v为每小时单星的储存成本，c为每小时单星的短期成本，Kk为tk时刻地面备份星数，n为卫星生产和发射事件的总数，Mi为ti时刻星座故障卫星数，j为卫星替换和故障事件的总数，T为运行时间。

3.2.2.4 备份策略仿真评估

将数据库中的卫星可靠性数据导入星座备份策略分析评估模块，并输入其它时间变迁参数和成本参数，然后选择星座备份策略，包括：地面备份星数、每个轨道面在轨备份星数和备份星发射方式，通过设置仿真条件对其进行评估以获得相应的星座性能参数。最后，利用可视化功能对不同星座备份策略的评估结果进行可视化处理，并选出最优的备份策略。

3.2.3 在轨备份星轨位设计模块

在轨备份星轨位设计模块通过建立轨位优化模型，利用多目标优化算法对备份星轨位进行优化设计，以实现对星座性能的增强效果。

在轨位优化模型中，优化变量为每个轨道面上备份星的轨位fi，j，其中i为轨道面编号，j为在轨备份星编号，轨位范围为[0°，360°]。以PDOP值和可见卫星数作为评价指标，采取网格分析法[16]，对导航星座的服务区域进行网格划分，并统计每一时刻下所有网格点的PDOP值和可见卫星数，从而可得到服务区域内PDOP值和可见卫星数的平均值，分别用FP(X)和FM(X)表示。因此，轨位优化模型的目标函数为

(5)

然后采用NSGA-Ⅱ算法对备份星轨位进行优化求解，该算法采取快速非支配排序法，通过定义拥挤距离来计算各层中点之间的拥挤度[17]，主要包括初始化、选择、交叉和变异等步骤。

3.3 软件界面设计

软件采用 Windows 界面程序标准，菜单和快捷按钮相结合，具有载入、保存、编辑修改、输出等功能。图3为软件启动界面。

图3 中轨道Walker导航星座备份策略分析仿真软件启动界面

通过软件启动界面中卫星可靠性分析、备份策略分析评估以及备份星轨位设计按钮进入相应的功能模块，各功能模块界面如图4-6所示。在软件模块程序的运行过程中，利用Matlab的GUI界面实现参数的输入、输出，用对话框的命令方式进行操作和控制，通过数据库和访问服务实现数据库和外部信息的交换，实现了良好的人机交互功能[18]。

图4 卫星可靠性分析模块界面

图5 星座备份策略分析评估模块界面

图6 在轨备份星轨位设计模块界面

4 应用实例

4.1 卫星可靠性分析

假设卫星工作时间为105小时，工作寿命末期为8.76×104小时。在卫星可靠性分析模块中输入电源系统底事件的失效率，如表2所示，得到电源系统的可靠性曲线如图7所示。

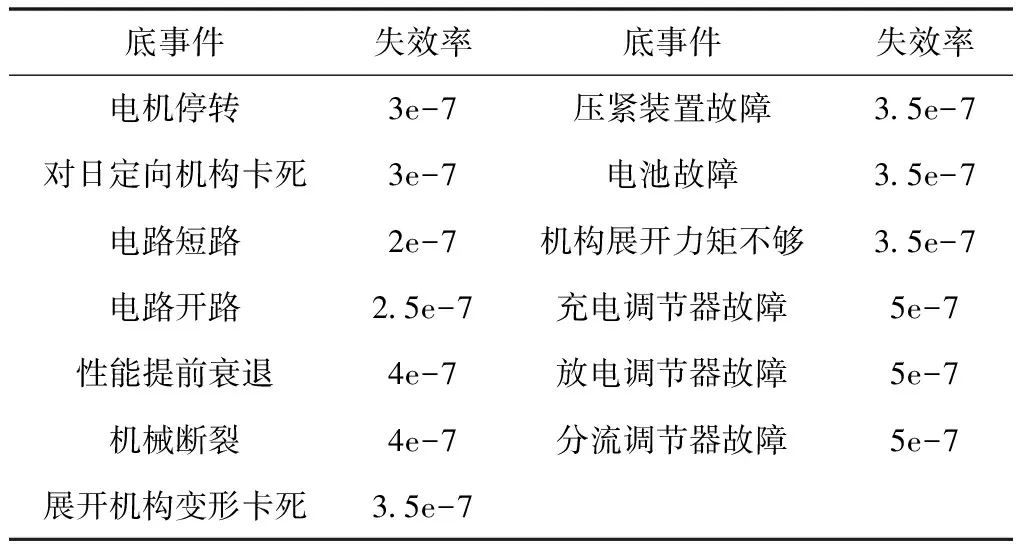
表2 电源分系统各底事件失效率

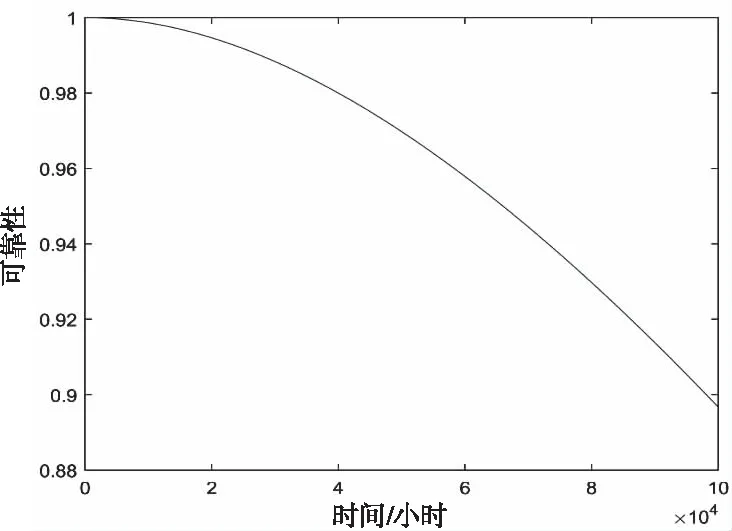
图7 电源分系统的可靠性曲线

同理，可对姿轨控和推进分系统进行分析，并结合其它系统得到卫星随机故障模型的可靠性曲线如图9所示。由图8可知，随着工作时间的增加，卫星及其分系统的可靠性在逐渐下降，同时电源系统对卫星可靠性的影响在逐渐增大，到寿命末期时成为三个分系统中最为薄弱的环节。

图8 卫星随机故障模型的可靠性曲线

最后，输入损耗故障模型参数，其中期望为9.3×104，标准差为104，从而得到卫星可靠性模型如图9所示。

图9 卫星可靠性模型

由图10可知，在早期阶段，卫星可靠性下降较为缓慢，当到达6×104小时时，卫星可靠性开始迅速下降，损耗累积的作用逐步显著，到达寿命末期8.76×104小时时，卫星的可靠性为0.59，此时损耗累积已成为影响卫星可靠性的主要因素，至工作时间105小时时，卫星可靠性仅为0.2。由此可得，该软件能实现对卫星早期故障和损耗累积过程的描述，从而建立更为准确的卫星可靠性模型。

4.2 星座备份策略分析评估

通过导入卫星可靠性模型获得单星STPN模型中长期故障变迁的参数。其它时间变迁参数和成本参数如表3-4所示。

表3 星座STPN模型时间变迁的速率参数

表4 成本模型中的成本参数

假设星座运行时间为10年，火箭发射成功率为0.97，利用蒙特卡洛方法对不同备份策略进行103次仿真。针对每个轨道面在轨备份1颗，地面备份0～8颗，备份星采用一箭一星发射方式的备份策略进行可用性和成本分析，结果如图10-11所示。

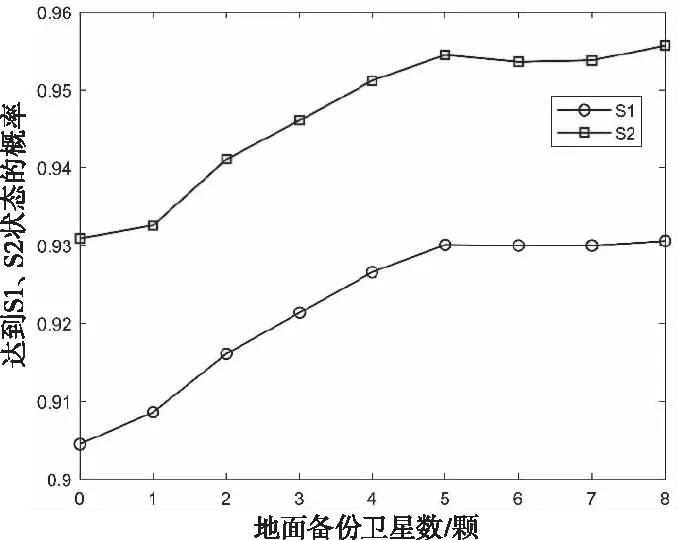
图10 每个轨道面备份1颗时备份策略的可用性对比分析图

从图10可得，对于每个轨道面在轨备份1颗的备份策略，随着地面备份星数的增加，星座服务可用性也逐渐增加，当地面备份星数达到5颗时，概率趋于平稳，此时达到S1和S2状态的概率分别为93.01%和95.45%，满足备份策略的设计要求。

图11 每个轨道面备份1颗时备份策略的运行成本对比分析图

从图11可得，随着地面备份星数的增加，成本也会随之增加。因此，通过比较不同备份策略的评估结果，可以选择地面备份星数为5颗的备份策略，该策略不仅能满足服务可用性的设计要求而且能使运行成本最小化。

同理，通过改变备份策略中在轨备份星数以及备份星发射方式，可对其它备份策略进行评估分析，最终得到星座的最优备份策略。

4.3 在轨备份星轨位设计

依据优化模型及算法对每个轨道面在轨备份1颗的备份策略进行轨位设计，以5°×5°的网格对全球区域进行划分，仿真时间为一个星座回归周期，数据统计步长为600s。优化算法的种群个数N为50，最大进化代数G为50，交叉因子为1，变异因子为0.16。在轨备份星轨位优化结果如图12所示。

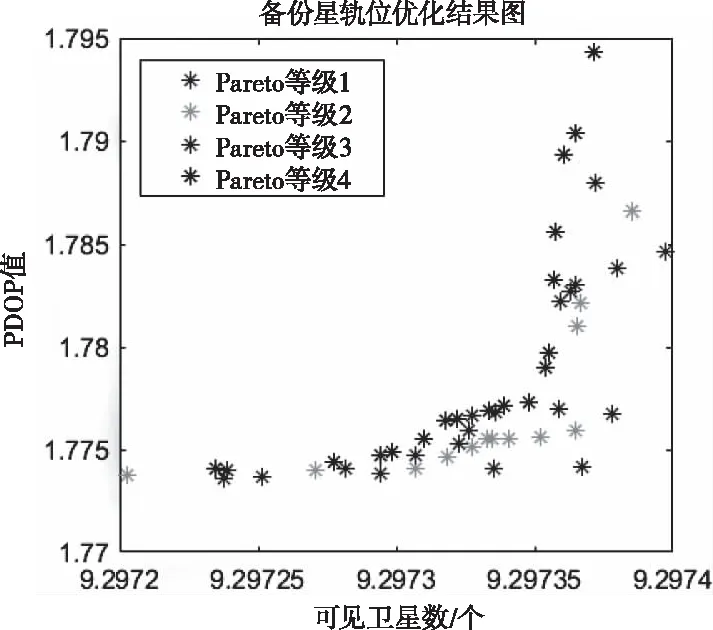
图12 在轨备份星轨位优化结果

从图12可得，对于优化解集中不同的解，其可见卫星数的变化范围较小，而且在这小范围内，PDOP值随着可见卫星数增大而增大。最终，从优化解集中筛选出非支配解集，即图中的Pareto等级1，并按照PDOP值进行升序排列，如表5所示。

表5 在轨备份星轨位的非支配解集

从表5可得，可见卫星数变化范围较小，因此选择非支配解集中PDOP值最小的解作为最优解，即f1，1=70.1°，f2，1=172.9°，f3，1=274°，最优解的在轨备份星轨位空间示意图如图13所示。

图13 在轨备份星轨位空间示意图

由仿真结果可得，在轨备份星轨位设计模块能实现对备份策略中在轨备份星轨位的优化设计，从而提高导航星座的服务性能。

5 总结

本文开发了中轨道Walker导航星座备份策略分析仿真软件，实现了卫星可靠性分析、星座备份策略分析评估和在轨备份星轨位设计等基本功能。该软件能有效地模拟卫星随机故障的动态行为，描述卫星早期故障和损耗累积过程，有利于分析卫星的薄弱环节，进而建立更为准确的卫星可靠性模型，为星座备份策略的分析评估提供数据支持。同时，该软件可以评估不同的备份策略，具有较好的灵活性，所得的最优备份策略不仅能满足星座可用性的设计需求，而且能实现运行成本的最小化，并且还能对备份策略中的在轨备份星轨位进行优化设计，从而提高星座的服务性能，可为其它卫星星座备份策略的设计提供借鉴。