基于杂波频谱统计的平台与目标速度估计方法
2022-08-22黄晓红邓振淼
黄晓红,赵 焱,邓振淼
(1. 华北理工大学人工智能学院,河北唐山 063200;2. 华北理工大学电气工程学院,河北唐山 063200;3. 厦门大学信息科学与技术学院,福建厦门 361001)
1 引言
毫米波雷达具有体积小、质量轻和空间分辨率高的特点。与红外、激光等相比,毫米波雷达穿透雾、烟、灰尘的能力强,具有全天候(大雨天除外)全天时的特点,此外,毫米波的抗干扰、反隐身能力也优于其它微波。毫米波雷达是测量被测物体相对距离、速度、方位的高精度传感器,早期被应用于军事领域,随着雷达技术的发展与进步,毫米波雷达传感器开始应用于汽车电子、无人机、智能交通等多个领域。
冀振元等学者在1999年就LFMCW信号在高频雷达中的应用作了具体分析,在此基础上,利用二维快速傅里叶变换(Two-Dimensional Fast Fourier Transform,2D-FFT)处理技术对目标回波信号的信息提取进行了仿真,并对实验结果作了分析,得到了较好的性能[1]。王月鹏等学者在2005年,针对LFMCW在动目标检测上存在一定难度,利用2D-FFT处理技术对目标回波信号相位信息进行提取,可有效地抑制固定杂波,并对2D-FFT的具体应用约束和算法的复杂度作了分析[2]。刘文彬等学者在2015年针对LFMCW检测动目标存在一定难度,利用2D-FFT技术对目标信息进行提取,详细说明了数据的缓存、实数序列FFT的算法等,最后测试结果表明,2D-FFT算法能很好的提取出目标的距离和速度[3]。以上文献都是针对LFMCW雷达在动目标检测上存在一定困难这一问题,提出了通过2D-FFT或者频谱分析、动目标检测等算法实现目标距离和速度的估计,但是这些算法都有一定缺陷,就是当雷达处于运动平台时,若平台的速度未知,这些目标检测算法都会出现虚警现象导致雷达无法正常工作。
本文提出了一种基于杂波频谱统计的非平稳平台雷达与目标速度估计算法,通过CFAR提高目标检测性能的同时,对雷达接收到的目标和周围环境的回波进行分析,判断回波中是否存在杂波,并估计杂波的速度,在平台运动的情况下,杂波速度近似为雷达运动平台的速度。通过对杂波速度所在的速度维度进行统计得到杂波频谱的阈值,对阈值进行判断处理,来滤除一定范围内的杂波,得到被探测目标的速度。
2 D-FFT目标参数估计算法
对于目标的检测是雷达最基本的工作,为了得到更多的工作带宽,实际应用中常使用频率或相位调制,在毫米波雷达中常使用LFMCW对回波信号从距离维和速度维两个维度进行参数估计[4]。
在一个周期T内雷达发射信号的表达式可以写为
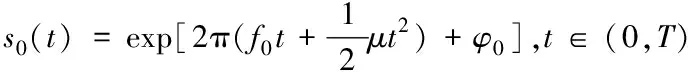
(1)
其中,f0为信号的中心频率;μ为信号的调频斜率;φ0是信号的初始相位。
若存在运动目标距离雷达为r,速度为v,回波时延τ为

(2)
其中,c为光速。接收信号sr(t)的表达式为
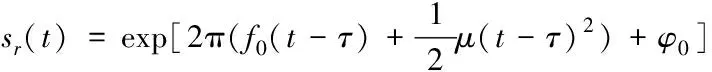
(3)
去斜处理后的差频信号sb(t)的表达式为
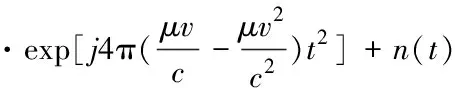
(4)
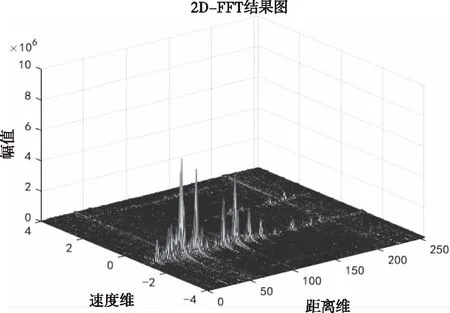
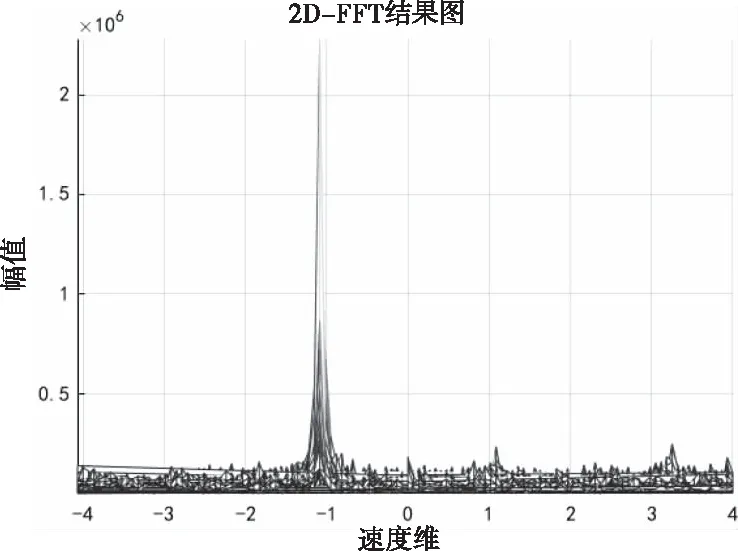
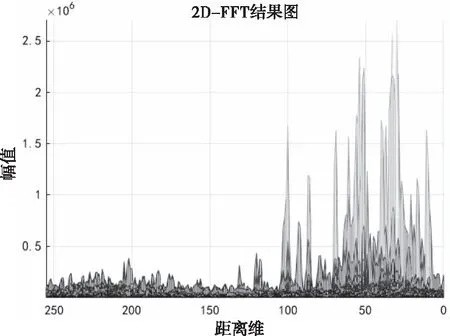
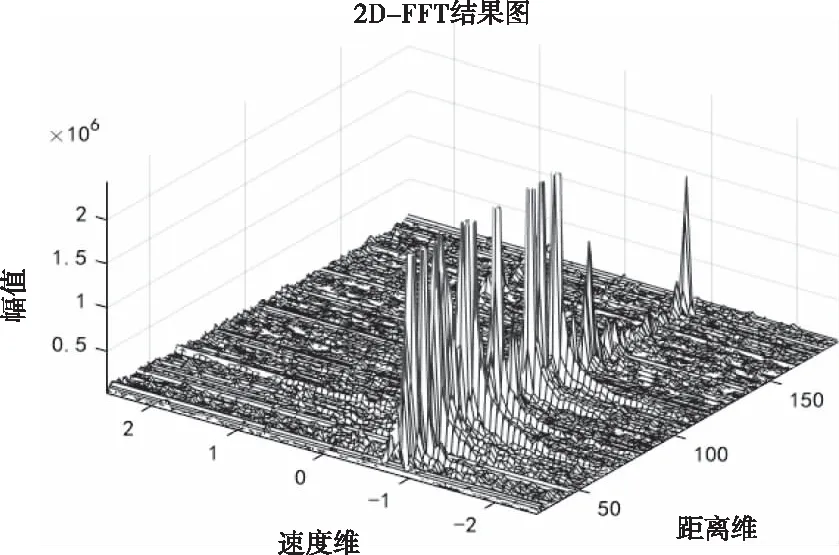
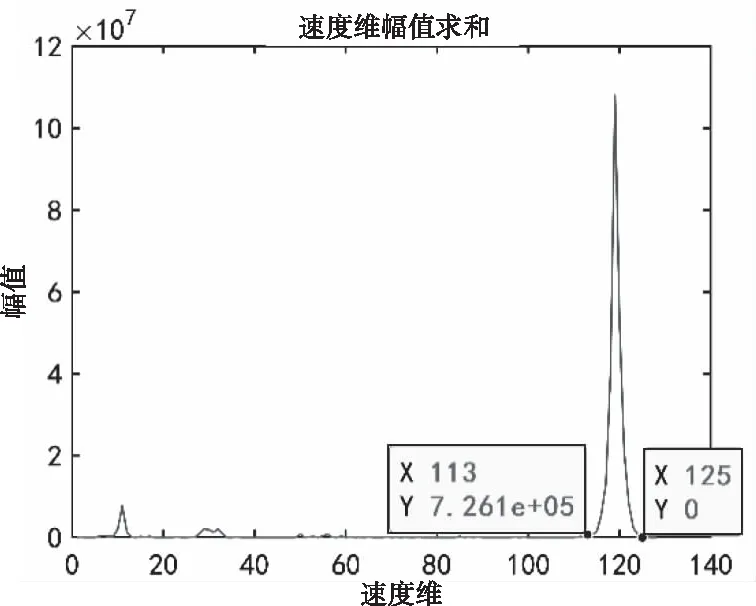
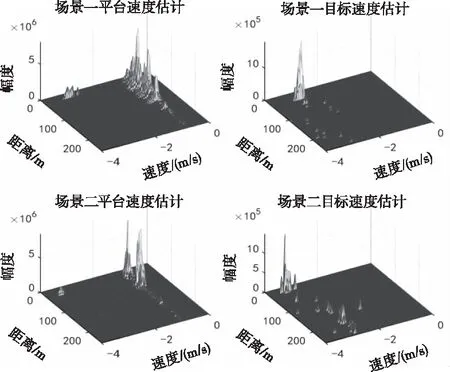
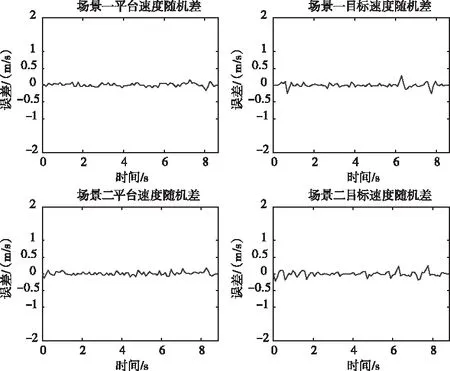
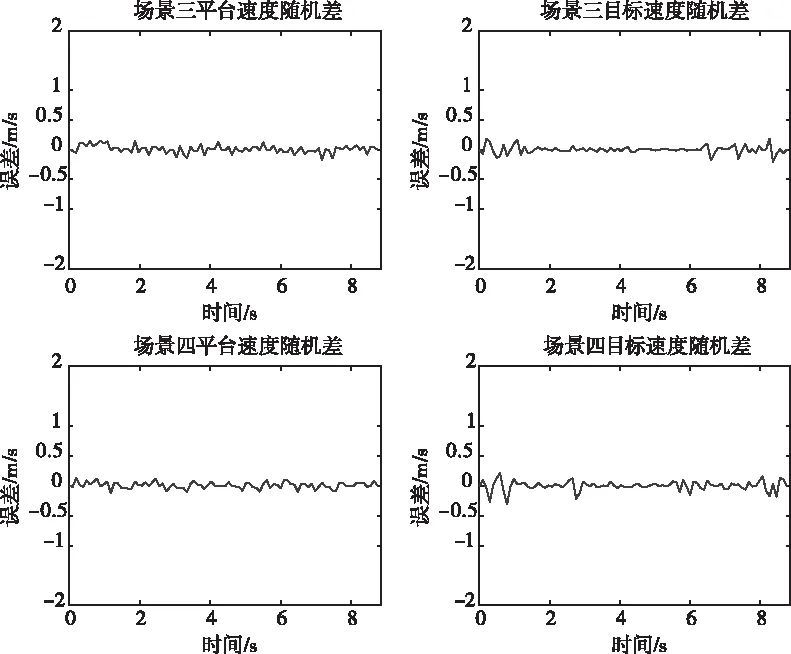
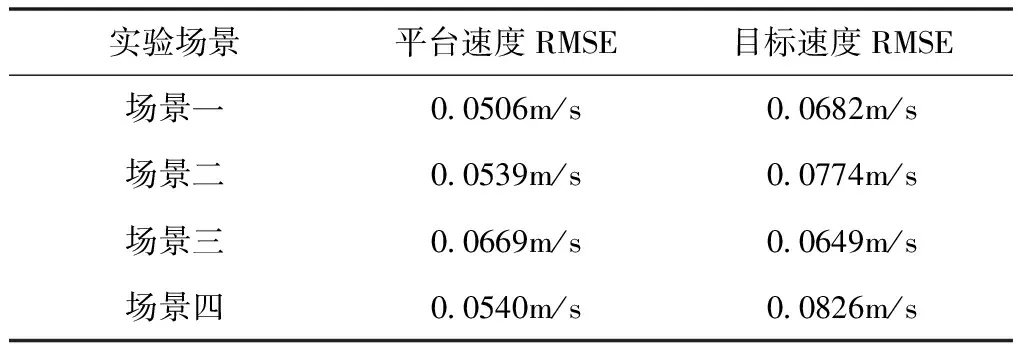
其中,n(t)为噪声,并且2μrv< sb(t)=Aexp[j(2πfbt+φb)]+n(t) (5) 其中,A为频谱幅度。φb为 (6) fb为求得的差频频率为 (7) 观察式(7),可知fb是由目标的距离和速度决定的,需要同时知道fr和fd才可以得到目标的距离和速度。 假设雷达采样频率为fs,由式(4)可知,单周期T内的差频信号为 (8) 其中,w(n)为窗函数;n为快时间维的采样点数。对M组差频信号进行积累,表示为 (9) (10) 对M×N的矩阵进行2D-FFT处理后的表达式为 (11) (12) (13) 目标在距离维频谱上的位置p为 (14) 对积累的周期M做处理后可得目标速度产生的fFFTv为 (15) (16) 最后,通过2D-FFT算法产生的距离多普勒(Range Dopple Matrix,RDM)图上得到目标的谱峰位置(p,q),则目标的距离和速度信息为 (17) 雷达接收的杂波,由多方面原因所造成,同雷达本身的工作状态(入射角、载频、极化方式、波束宽度等)和雷达工作的背景情况(障碍物数量、障碍物反射强度、天气等)都有关系。一般能够将杂波分为两类:固定杂波和运动杂波,雷达运动状态下产生的杂波为运动杂波,这类杂波的多普勒频移不为零[5]。 若雷达处在运动状态下时,即使检测区域内没有运动的目标,但因为此时检测范围内的静止目标相对雷达也有了速度,因此能够在频谱上看到存在目标尖峰,而目标的速度值就是雷达相对于静止目标的径向速度。图1是当检测区域内没有真实运动目标情况下,雷达运动状态下的2D-FFT结果图。可以看到即使没有真实运动的目标,在2D-FFT的频谱图上依旧可以看到大量尖峰,这些尖峰在经过一维CFAR后都会被当作目标检测出来。图2是从速度维观察雷达运动状态下的频谱图,运动后的雷达使得杂波相对于雷达有了一个相对的速度,并且杂波的峰值在速度维上是比较一致的。图3是从距离维观察雷达在运动状态下的频谱图,在整个距离维上,都有高低不同的尖峰,这是因为在整个探测范围内的固定目标都有了相对速度,有的目标反射强,有的目标反射弱。在CFAR处理后,这些尖峰都会被当成目标检测出来,但真实情况下并没有真实的运动目标,传统的二维检测算法在平台运动速度未知的情况下,在运动平台上的目标检测容易出现大量虚警的问题,给雷达工作造成极大的干扰,而本文提出的算法,就是通过雷达在运动状态下杂波频谱图展现出来的特性,分析处理后,滤除固定目标和杂波造成的干扰。 图1 雷达运动状态下的2D-FFT图 图2 雷达运动状态下的2D-FFT速度维视图 图3 雷达运动状态下的2D-FFT距离视图 当雷达运动状态下,2D-FFT产生的RDM图在某一个速度单元上有长度持续整个距离维的一段尖峰,并且这个速度将随着雷达的运动速度不断变化,由相对运动可知,这个速度的值就是雷达本身的运动速度。但从频谱上看,速度维的峰值虽然集中,但也存在一定的扩散现象,因为雷达检测到的速度为目标的径向速度,所以除了目标相对于雷达的径向速度,还与目标和和雷达波束的夹角及雷达波束宽度有关[6]。图4是雷达运动状态下2D-FFT局部放大结果图。在频谱上放大看,速度维上的整条尖峰并不是在一个速度维上分布,而是略有发散的[7]。 图4 雷达运动状态下2D-FFT局部放大视图 在这种情况下,需要得知雷达的速度,即杂波的速度,然后在进行运动目标检测时,滤掉一定范围内的杂波,才能滤除固定目标和杂波,检测出真正运动的目标。因此本文通过对杂波的特性分析后,检测出雷达运动平台的速度,并通过寻找阈值来滤除固定目标和杂波造成的虚警。 基于杂波频谱统计的非平稳平台雷达与目标速度估计算法的重点是如何判断是否是杂波并较精确地估计杂波速度,假设速度维需要检测的速度单元个数为N,距离维需要检测的距离单元个数为M通过对杂波频谱的观察,杂波所在的速度单元都集中在一定阈值内,且回波数据中杂波所在的区域峰值远大于目标[8][9],通过对杂波数据的分析得到 (18) 其中,Aj为同一速度单元上每个目标回波的幅值,Ak为每个速度单元上目标幅值的总和,A为所有速度单元上幅值最大的值。 图5 滤波前速度维幅值求和图 如图5所示,统计得到速度维上杂波的幅值都集中在113-125之间的速度单元内,由于杂波速度在速度维上存在扩散现象,因此应该对估计得到的多次杂波速度取均值,即 (19) 其中,v为最后估计得到的杂波速度即雷达运动平台的速度,m为可能的杂波速度的个数,A为最大幅值所在的速度单元,vres为雷达速度分辨率。 因为杂波的频谱都集中在一定的范围内,将一定阈值内的杂波滤除,即可得到目标峰值的位置,即目标的速度[10]。 (20) 其中,f′(Ak)为相邻速度单元目标幅值总和的斜率,Ak(i)为每个速度单元幅值总和所在的速度单元。判断幅值所在速度单元两侧的波谷,即可得到杂波频谱所在的范围,即在波峰左侧寻找杂波频谱所在的范围时, (21) 其中,ε为所允许的检测误差,在波峰右侧寻找时,需要判断是否存在f′(Ak)>0的位置即 (22) 如图6所示,在滤除杂波后,最大峰值所在的速度单元的位置即为目标的速度,即 V=A1·vres (23) 图6 滤波后速度维幅值求和图 其中,V是估计得到的目标的速度,A1是滤除杂波后所有速度单元上幅值最大的值。 本实验算法流程如图7所示。对回波数据进行2D-FFT和一维CFAR运算,得到目标和杂波所在速度维的阈值,对杂波频谱进行统计得到杂波峰值,取多次估计结果的平均值即为杂波的速度,即雷达运动平台的速度。判断杂波频谱阈值的范围的边界,若为杂波频谱的边界则输出杂波所在的范围,滤波后,输出运动目标的速度值。 图7 算法流程图 为了进一步测试雷达信号处理算法的准确性和稳定性,笔者选取了四个杂波环境不同的场景来进行外场试验。本次实验使用的是24GHz交通雷达,工作带宽为150MHz,积累周期数为128,单周期的采样点数为256,距离分辨率为1m,速度分辨率为0.06m/s,本次实验中利用两个人体对象来模拟两个同时运动的目标,将雷达固定在一个人体对象胸前保持匀速直线运动来模拟雷达运动平台,在雷达前方约5米处,另一个人体对象与雷达平台同时朝同一方向做匀速直线运动来模拟被探测的运动目标。四个不同场景如图8所示,基于杂波频谱统计的测速算法如图9,10所示。 图8 实验场景一(左上)实验场景二(右上)实验场景三(左下)实验场景四(右下) 图9 第一、二场景平台和目标速度估计 图10 第三、四场景平台和目标速度估计 在图9、10中观察到四个不同场景下,目标运动速度约在3m/s,平台的速度约在1m/s,杂波随着雷达速度变化而变化,由相对运动可知,这个速度就是雷达平台的速度,只是方向不同。经过本文算法之后,可以看到杂波的峰值及峰值左右发散部分已经被完全滤除掉,只剩被检测目标的峰值以及周边一些峰值较小的回波,目标的速度可以精确的估计出来。 如图11、12所示,通过随机差来判断四个不同场景估计得到的速度值,可以观察到,不同场景估计得到的结果,均在正负0.5m/s之间波动,不同场景估计结果的RMSE的值如表1所示,雷达运动平台四个场景估计得到的平均RMSE为0.056m/s,被探测目标四个不同场景估计得到的平均RMSE为0.073m/s。实验结果表明:在不同的场景下,运动平台和目标速度的结果与真实结果误差较小,验证了算法的稳定性和准确性。 图11 一、二场景平台和目标速度估计随机差 图12 三、四场景平台和目标速度估计随机差 表1 四个不同场景速度估计值的RMSE 本文针对雷达目标检测算法只适用于雷达在静止情况下对运动目标的检测,若雷达处于运动平台上,在平台速度难以得知的情况下,会给雷达的目标检测工作造成很大干扰这一问题,提出了一种基于杂波频谱统计的非平稳平台雷达与目标速度估计的雷达信号处理算法,通过分析杂波频谱特性实现对雷达运动平台和目标速度的估计,通过外场试验验证了在不同场景下该算法的有效性,该算法可以为雷达运动平台下的目标检测算法提供参考。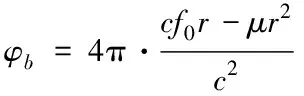
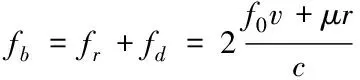

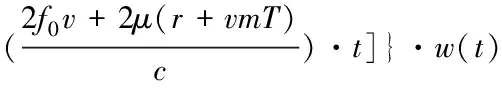
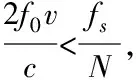


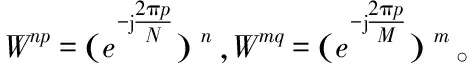
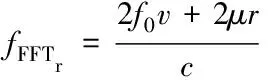

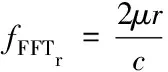

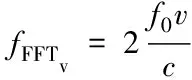
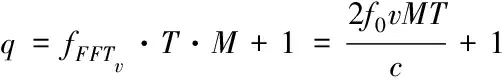
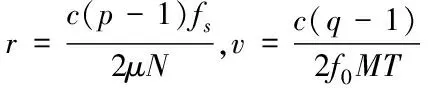
3 雷达平台运动下的2D-FFT
4 基于杂波频谱统计的速度估计算法
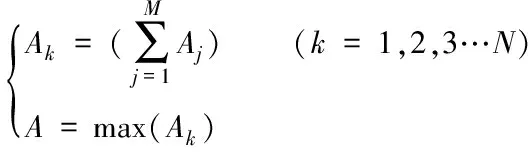
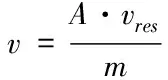
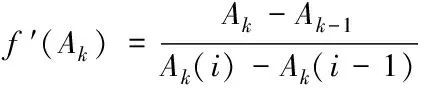




5 实测数据分析


6 结束语
