河流砂碎屑统计方法的对比实验研究

2022-08-20董小龙胡修棉郭荣华赖文

沉积学报 2022年4期

关键词：碎屑粒径偏差

董小龙，胡修棉，郭荣华，赖文

1.南京大学地球科学与工程学院，南京 210023

2.南京大学地理与海洋科学学院，南京 210023

0 引言

碎屑统计是确定砂或砂岩的物质组成、判定其物源的重要研究方法。通常选取具有代表性的砂或砂岩样品磨制成薄片，在显微镜下进行定量统计。统计方法大致可分为点记法和面积法两类，其中点记法最为常用。

一般而言，点记法就是通过获得各类型颗粒的点数来代表其相对含量，分析岩屑的成分和比例，并通过Q/F/L 三角图来展示[1-5]。早期地质工作者采取统计薄片中所有或某个区域内的颗粒来获得整个样品的物质组成和相对含量[6-7]。然而该方法统计工作量大，而且统计的结果不能转化为碎屑组分的面积比[8]。Glagolev[9]和Chayes[1,10]提出用网格节点计数法来统计碎屑颗粒，并由Galehouse[8]系统总结形成完整的Glagolev-Chayes 统计方法，该方法获得的统计结果能够转化为相应的面积比[11]。随后，以Basu[2]和Suttner[3]为代表的学者提出，通过筛选出中粒砂来进行碎屑统计才具有意义。这种方法影响了后续的许多学者[12-14]，然而，这种“窄粒径”范围受等效沉降作用的影响较大，不同粒径的选择性统计会对结果造成较大的偏差[11,15]。随后由Gazzi[16]和Dickinson[17]提出、Ingersollet al.[4]对其系统总结的Gazzi-Dickinson统计法，对“窄粒径”碎屑统计方法提出了质疑，并明确指出Gazzi-Dickinson 统计法不需要对样品粒径进行筛选，对同一样品不同粒径的颗粒进行统计，结果更集中，而传统方法更分散。Gazzi-Dickinson法在基于以薄片为研究对象的碎屑物源分析中发挥了重要作用，被后续研究者的广泛接受和采纳[5,18-19]，成为砂或砂岩碎屑统计分析的主流方法。然而，也有学者指出Gazzi-Dickinson 统计法仅适合用于构造环境分析而不适于气候、搬运历史和成岩作用的解释[4,20-21]，无法改变水动力分选对统计结果的影响[22]。

面积法早期采用标准对比来近似估计颗粒的面积[23-25]，然而这种方法受个人因素影响太大，所估计的结果也不够准确。近年来，随着图像分析技术的迅速发展，一些地质工作者利用ImageJ 和Photoshop等图像分析软件精确计算显微图片中各颗粒类型的面积[26-27]，使得获得颗粒面积成为了可能。

以上两类方法面临的共同问题是，需要统计多少个颗粒才具有代表性。Ingersoll[28]提出的统计数量为500颗，而随后Ingersollet al.[4]又提出统计数量300颗能够达到统计要求。而现今大多数学者统计400颗以上[5,18-19,29]。目前，在碎屑统计中没有一个定量的标准，也缺乏实例的验证和模拟。另一方面，在统计过程中影响统计结果的因素有哪些？是否需要考虑粒径的大小，分选程度对统计结果有何影响。四种不同的统计方法对同一样品的统计结果有何差异性？点记法所得到的统计结果能够代表颗粒的真实面积比吗？这方面的研究和报道也极少。

本次实验以青藏高原雅鲁藏布江干流的河流砂为研究对象，采用薄片实际统计和Matlab 模拟统计两种方法，以期明确不同的统计方法统计结果的差异性，评估颗粒分选程度和颗粒含量对统计结果的影响。用实验统计结果验证统计数量需要达到多少颗时才能够达到统计学要求，以及在统计中应该注意的事项，并针对不同应用场景给出建议统计方法。

1 样品和统计方法

1.1 样品

本次研究选用2016年6月采集于雅鲁藏布江干流心滩位置的河流砂样品16A063（日喀则市附近，GPS 坐标：29°19′13.5″N，88°51′28.4″E）和16A064（拉萨贡嘎机场附近，GPS 坐标：29°16′50.00″N，91°10′29.00″ E）（图1），用63 μm 和2 000 μm 的筛网干筛获得粒径在63～2 000 μm的砂样，两个样品在该粒径范围内的质量分别为：16A063为89.3%；16A064为91.5%，代表了主要的物质组分。用分样器均分得到4 份样品，每份约2 g。每个样品各磨制标准光学薄片4张供碎屑统计分析。

1.1.1 样品粒度和分选

利用Nikon NIS Elements图像分析软件测量颗粒面积，同时计算每个颗粒的周长、长轴粒径和短轴粒径。本次研究采用长轴粒径作为颗粒粒径，根据公式Ф＝-log2D 进行单位换算，其中“D”是以毫米为单位的颗粒直径，粒度分选计算公式为：δΦ=（Ф84-Ф16）/4+（Ф95-Ф5）/6.6，分选可描述为：1)δΦ＜0.35 分选很好；2)δΦ=0.35～0.50 分选好；3)δΦ=0.50～0.71 分选中等偏好；4)δΦ=0.71～1.00 分选中等；δΦ=1.00～2.00 分选差；δΦ＞2.00 分选极差[30]。计算得出δΦ（16A063）=0.79，δΦ（16A064）=0.64。样品16A063 共测得粒径个数2 511 颗，粒度范围主要为2～4 Ф，粒度中值为3 Ф，以细粒和极细粒为主（图2a）；样品16A064共测得粒径个数2 252 颗粒度范围主要为1～3 Ф，粒度中值为2.6 Ф，以中细粒为主（图2b）。可知样品16A063分选中等，样品16A064分选中等偏好。

1.1.2 样品均匀性

利用IBM SPSS Statistics 26.0软件进行卡方检验来判断样品是否分布均匀。将每张薄片统计的颗粒随机分成不同容量的不同组别，以50 为公差递增统计，从0 至500 颗共11 个不同容量的组别，在每个容量内统计出不同类型颗粒百分比，比较各组之间同一类型颗粒的含量百分比变化情况。卡方检验计算得到P 值（显著性），当P 值均大于0.05，则认为该容量下的颗粒均匀分布。

样品16A063 的组别容量达到150 时，该样品内的所有颗粒类型均匀分布（图3a1，b1）；样品16A064的组别容量达到200时，该样品内的所有颗粒类型均匀分布（图3a2，b2）。当颗粒容量仅有150颗时，仅有Q/F/L 三大类呈现均匀分布。两个样品随机选取的颗粒大于200 颗时，该容量内的7 小类颗粒均匀分布。因此，从统计的角度来看，只要统计的颗粒数大于200颗，这两个样品都达到均匀分布的要求。

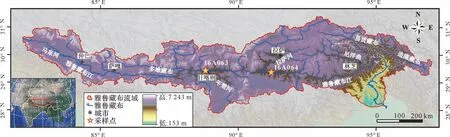
图1 雅鲁藏布江流域及本文河流砂样品位置图Fig.1 Simplified map of the Yarlung Tsangpo River drainage basin showing locations of studied river sand samples

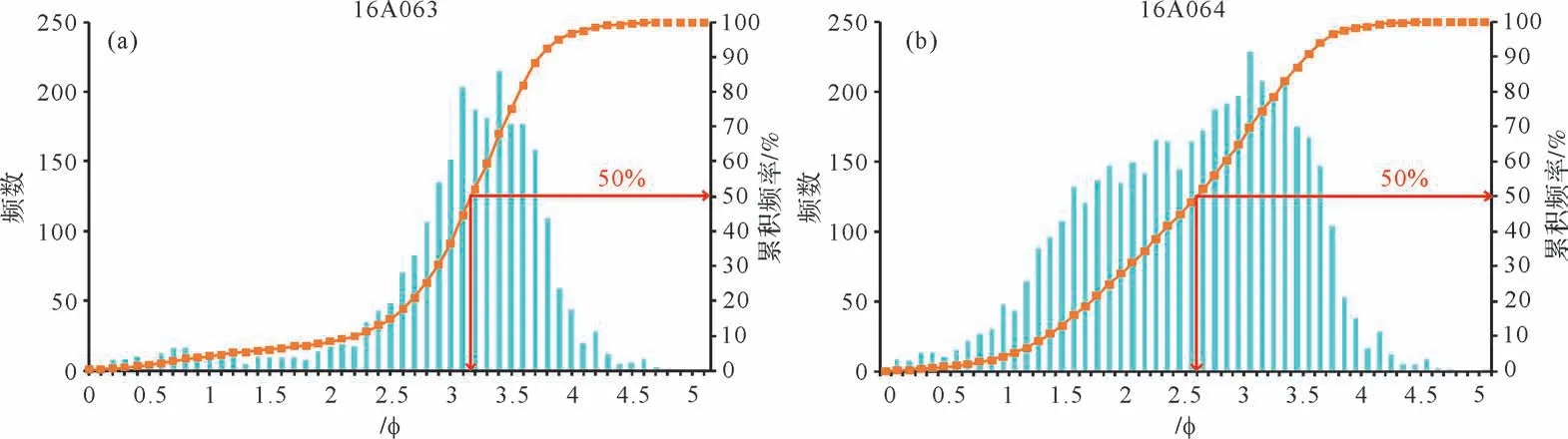
图2 两个河流砂样品的粒径概率累积曲线与频率直方图Fig.2 Cumulative grain size probability curves and frequency histograms for two studied samples

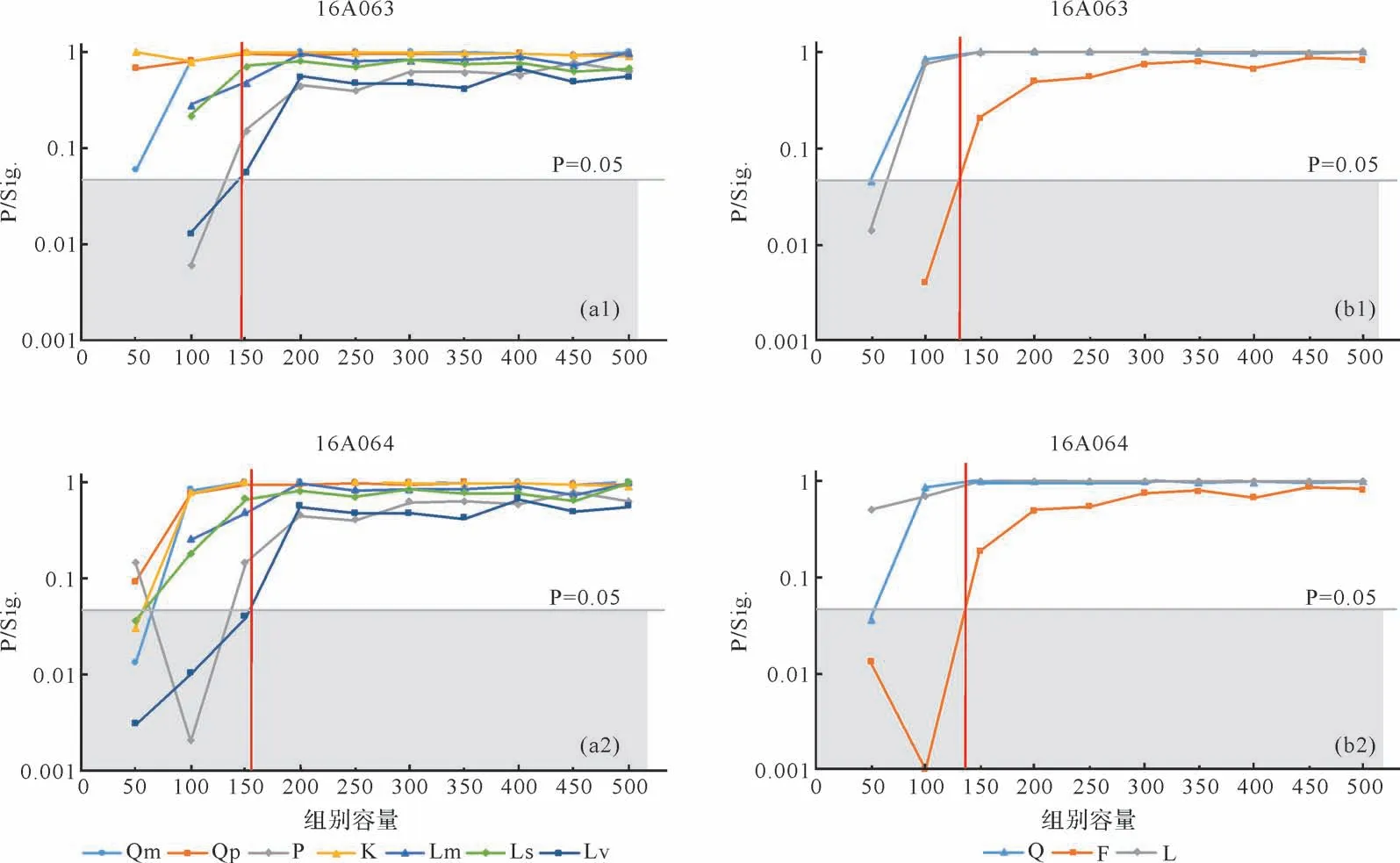
图3 SPSS 卡方检验颗粒分布均匀性纵坐标P（Sig.）为显著性，当P值大于0.05时则认为该容量下的颗粒均匀分布；横坐标为不同的容量从0至500，间距为50递增；Qm.单晶石英；Qp.多晶石英；Q.石英；P.斜长石；K.钾长石；F.长石；Lv.火山岩岩屑；Ls.沉积岩岩屑Fig.3 SPSS chi-squared test of uniform grain distributionThe vertical coordinates P(Sig.)represent the significance of chi-squared test.The grains are considered as uniformly distributed if P＞0.05.The horizontal axis represents volume of grains from 0 to 500 with a tolerance of 50; Qm. monocrystalline quartz; Qp. polycrystalline quartz; Q. total quartz; P. plagioclase feldspar; K. potassium feldspar;F.feldspar;Lv.volcanic rock fragments;Ls.sedimentary rock fragments;Lm.metamorphic rock fragments

1.2 统计方法

挑选混合均匀的薄片16A063和16A064各一张。对同一薄片采用具有代表性的四种统计方法（全颗粒法、全面积法、Gazzi-Dickinson 法和Glagolev-Chayes法）进行统计，具体方法介绍如下。

1.2.1 颗粒统计法

颗粒统计法包括全颗粒统计法和Gazzi-Dickinson法。

全颗粒统计法：在偏光显微镜下，对载玻片上一定区域内的所有颗粒逐一进行鉴定并统计，然后将统计的各类型的颗粒的数量换算后，得到各颗粒类型的百分含量（图4a）。

Gazzi-Dickinson 统计法：需要选择合适的栅格，栅格间距大于最大砂粒直径以避免重复计数。对落在栅格结点上粒径大于62.5 μm 的颗粒进行鉴定并计数，落在基质或胶结物上不计数。若一个大于62.5 μm 的矿物颗粒包含在岩屑中则单独计数。例如，玄武岩岩屑中>62.5 μm 的斜长石斑晶位于栅格结点上时，则需要标记为长石而不是岩屑[4]（图4c）。

图4 四种不同的碎屑统计方法示意图Fig.4 Four different detrital statistical methods

1.2.2 面积统计方法

面积统计法包括全面积统计法和Glagolev-Chayes法。

全面积统计方法：利用Nikon NIS Elements 图像分析软件进行统计，对颗粒类型进行鉴定，然后手动描出每一个颗粒边界，获得每个颗粒的类型和对应的面积，最终得到薄片中每种颗粒类型的总面积，然后换算成百分比（图4b）。

Glagolev-Chayes 统计法：同样是选择合适的栅格，将网格间距设置成小于颗粒的平均粒径，对落在粒径大于62.5 μm的碎屑颗粒上的网格节点均计数。落在基质或胶结物上的点则不计数。用于重矿物统计则根据实际粒径大小，选取合适的网格（图4d）。如Garzantiet al.[11]对粒径15～500 μm 的重矿物统计时选取的网格间距为125 μm。这种方法统计的节点数与颗粒的大小成正比，用节点数的多少来代表面积的大小，统计的结果能够转化为相应的面积百分比。

为了定量描述全颗粒法、Gazzi-Dickinson 统计法、Glagolev-Chayes统计法和全面积法统计结果的差异性，采用这四种方法对同一样品进行统计，对比统计结果。

1.2.3 Matlab模拟统计方法

为了更好地评估以上两类统计方法，基于Matlab编写的程序（附件），模拟显微镜下的碎屑统计过程。在Matlab 中随机生成颜色不同的圆或任意多边形，设置颗粒随机分布，调整不同颗粒间面积的相对比例和粒径大小等参数，来模拟在已知面积或者颗粒比例的情况下，用Gazzi-Dickinson统计法和Glagolev-Chayes统计法分别进行统计（图5），评估不同因素对抽样统计结果和实际情况的偏差。

设置等粒径等面积、等粒径不等面积、不等粒径等面积和不等粒径不等面积四种情况，模拟采用全颗粒法和Gazzi-Dickinson 法同时对这四种不同情况下的红、绿、蓝三色小球进行统计，以及模拟全面积法和Glagolev-Chayes 法同时在这四种情况下的统计。

2 河流砂碎屑组分统计结果

采用全颗粒法（颗粒法）、全面积法（面积法）、Gazzi-Dickinson 法（G-D 法）和Glagolev-Chayes 法（G-C法）统计的结果显示，样品16A063的Q/F/L比例分别为：45∶12∶44；29∶26∶45；41∶18∶41；31∶23∶46；Ls/Lv/Lm 的比例分别为：19∶14∶11；10∶28∶7；13∶19∶9；11∶27∶8（图6a，b、表1）。样品16A064 的Q/F/L比例分别为：45∶12∶44；29∶26∶45；41∶18∶41；31∶23∶46；Ls/Lv/Lm 的比例分别为：34∶7∶59；28∶9∶63；36∶9∶55；29∶9∶62（图6c，d、表1）。

2.1 全颗粒法与Gazzi-Dickinson方法的对比

同时采用人工统计和模拟统计，用全颗粒法与Gazzi-Dickinson方法统计的结果进行对比，比较这两种方法的差异性。

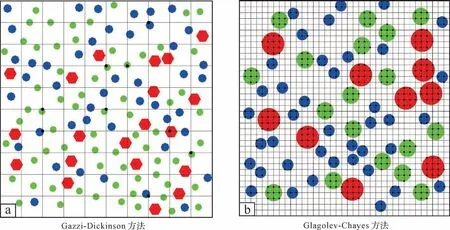
图5 Matlab 模拟Gazzi-Dickinson 法和Glagolev-Chayes 法统计Fig.5 Matlab simulation of Gazzi-Dickinson and Glagolev-Chayes statistical methods

图6 雅鲁藏布江干流河流砂典型显微照片（a，b）样品16A063正交偏光镜下显微照片；（c，d）样品16A064正交偏光镜下显微照片；Q.石英；P.斜长石；K.钾长石；Lv.火山岩岩屑；Ls.沉积岩岩屑；Lm.变质岩岩屑；S.蛇纹岩岩屑Fig.6 Photomicrographs illustrating the variation in the composition of sand from the Yarlung Tsangpo River(a,b) sample 16A063; (c,d) sample 16A064; Q. quartz; P. plagioclase feldspar; K. potassium feldspar; Lv. volcanic rock fragments; Lsm. mudstone rock fragments;Lsc.carbonate rock fragments;S.serpentinite rock fragments

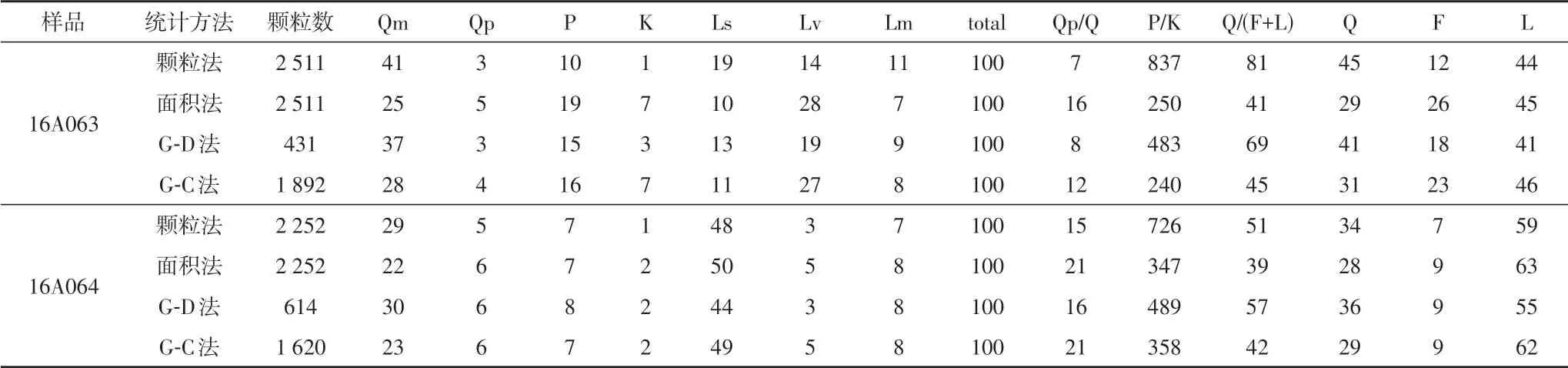
表1 样品16A063和16A064采用四种不同的统计方法得到的结果（%）Table 1 Statistical results for samples 16A063 and 16A064 using the four methods (%)

2.1.1 人工统计

采用全颗粒法与Gazzi-Dickinson 法对两个样品分别进行统计，样品16A063中两种方法的偏差范围为-83%～92%，样品16A064 两种方法的偏差范围为-52%～27%（图7a1，a2、表2）。两个样品无论是大类还是小类均表现出较大的偏差，说明Gazzi-Dickinson法统计结果并不代表该区域内的所有颗粒的统计结果，是由于两种方法本身的差异所造成的，如将含有大于62.5 μm斑晶的岩屑进行分解。

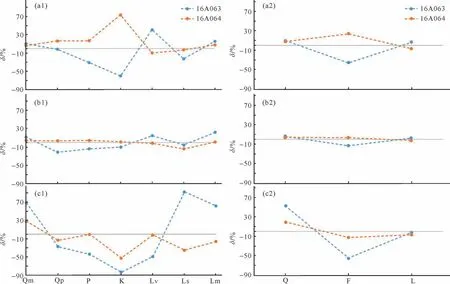
图7 四种不同的方法差异对比图（a1，a2）δ(%)=(G-D法-颗粒法)/颗粒法，表示以全颗粒法统计结果为标准，用Gazzi-Dickinson 方法与全颗粒法统计结果作标准偏差；（b1，b2）0δ(%)=(G-C法-面积法)/面积法，表示以全面积法统计结果为标准，Glagolev-Chayes法与全面积法统计结果作标准偏差；（c1，c2）δ(%)=(颗粒法-面积法)/面积法，表示以面积法统计结果为标准，全颗粒法与全面积法统计结果作标准偏差。全颗粒法=颗粒法，全面积法=面积法，Gazzi-Dickinson方法=G-D法，Glagolev-Chayes方法=G-C法Fig.7 Deviation of the four statistical methods(a1) grain method; (a2) Gazzi-Dickinson method; (b1,b2) Grain method taken as standard; (c1) Deviation between area method and Glagolev-Chayes method when area method is taken as standard;(c2)deviation between area method and grain method when the area method is taken as the standard (G-D=Gazzi-Dickinson method;G-C=Glagolev-Chayes method)

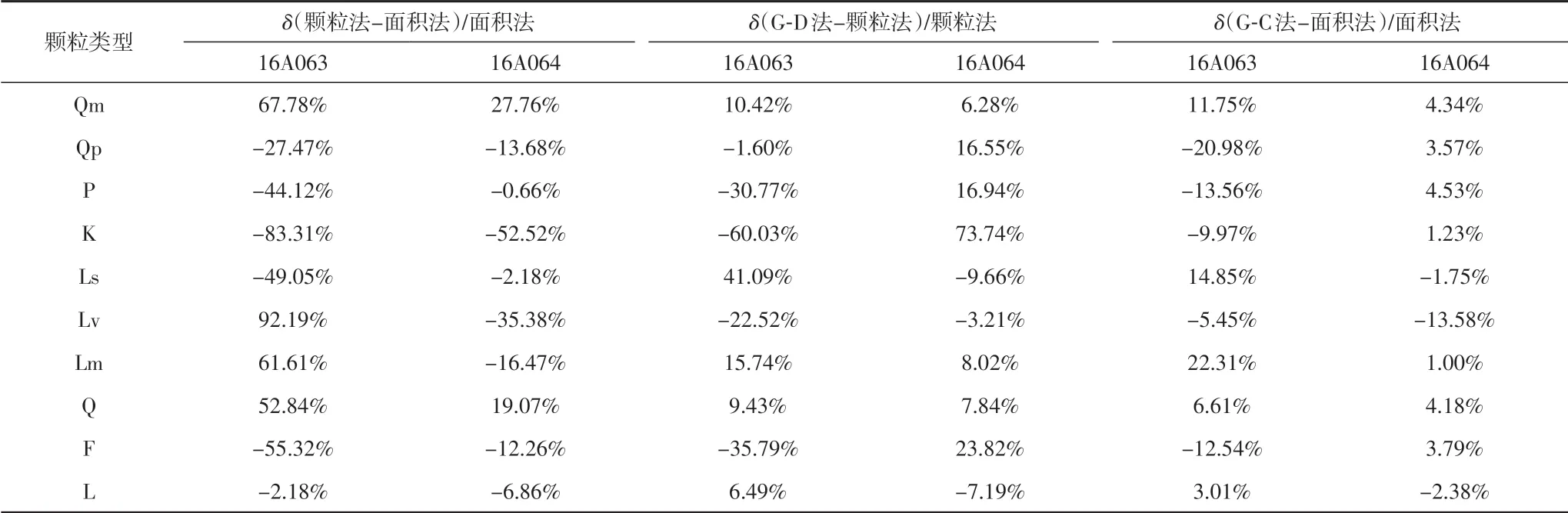
表2 四种不同的方法统计偏差表Table 2 Deviations of the four different methods

2.1.2 模拟统计

用Matlab 模拟采用全颗粒法与Gazzi-Dickinson方法对等粒径等面积、等粒径不等面积、不等粒径等面积和不等粒径不等面积四种情况下的红、绿、蓝三色小球进行统计，在等粒径的条件下两种方法的统计结果相近，偏差最大为15%，其他均小于5%；在不等粒径的条件下两种方法的偏差最大可达333%（图8）。说明在分选较好时，全颗粒法与Gazzi-Dickinson方法统计结果相近，在分选较差时，两种方法的统计结果偏差较大，Gazzi-Dickinson方法统计结果并不能完全代表全颗粒法统计结果。

实际统计表明Gazzi-Dickinson 法与全颗粒法存在一定的偏差，这种偏差是由于统计方法本身的差异所造成的，而模拟统计均表明在等粒径条件下Gazzi-Dickinson方法与全颗粒法统计结果偏差较小，在不等粒径条件下两种方法的统计结果偏差较大。

2.2 全面积法与Glagolev-Chayes方法的对比

2.2.1 人工统计

两个样品中，全面积法与Glagolev-Chayes 方法的统计结果相近，样品16A063 的偏差范围为-21%～22%，样品16A064 的偏差范围为-14%～5%（图7b1，b2、表2）。两个样品均表明无论是大类还是小类，两种方法的统计结果较为相近。

2.2.2 模拟统计

模拟采用全面积法与Glagolev-Chayes 方法统计，无论是等粒径还是不等粒径，两者的统计结果相近，偏差小于2%（图8）。

实际统计和模拟统计都表明Glagolev-Chayes 方法和全面积法的偏差较小，可以认为Glagolev-Chayes方法是全面积法的等效替代。

图8 不同情况下两类不同的统计方法的差异性（红、绿、蓝分别代表三种不同类型的颗粒）Fig.8 Deviations of the two statistical methods for different scenarios (red, green and blue=three grain types)

2.3 全颗粒法与全面积法的对比

两个样品均表现出全颗粒法与全面积法的统计结果有较大的差异，样品16A063 的偏差范围为-83%～92%，样品16A064 的偏差范围为-52%～27%。样品16A063 的分选较差，相较而言，样品16A063 采用全颗粒法和全面积法统计的偏差更大。说明样品的分选越差，全颗粒统计法和全面积法统计结果的差异性越大（图7c1，c2、表2）。

3 碎屑统计数量

将碎屑统计认为是抽样统计，对于随机分布的总体，按照绝对精度决定样本量n的公式为：

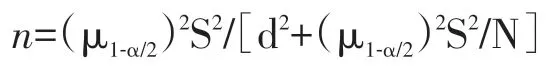
式中α为显著性水平；μ1-α/2是N（0，1）分布的1-α/2分位数；S2为总体方差，S2≈P（1-P）；d 为绝对精度（绝对误差）；N为样品总数，P为颗粒百分比[31-32]。

当α 取0.05 时，达到置信度为1-α=95%，此时μ1-α/2=1.96；当P 取0.5 时，有最大总体方差0.25，d 为绝对精度即绝对误差，一般取5%。可得到随着颗粒百分比的含量的增加，以及总体数量N的增加，所需抽样的样本容量曲线（图9）。

当样品总数N不断增加时，所需抽取的样本量n也不断增加。当N 趋于无穷大时，抽样数n为定值，此时：

n≈（μ1-α/2）2S2/d2

代入上式得：

n≈（1.96）20.5（1-0.5）/0.052≈384

所以对任意的样品，抽取的样本量达到384以上时，达到95%的置信度。

这个理论计算的数量是否符合实际样品的统计呢？我们将实际统计的两个样品进行验证。将面积法统计结果按照100 为公差累积统计，进行三角投图。从图10 中可以看出，对于样品16A063 来说，前400颗的统计偏差较大，而超过400颗后统计结果偏差相对较小，落点均位于同一岩性内。样品16A064投点均比较集中。

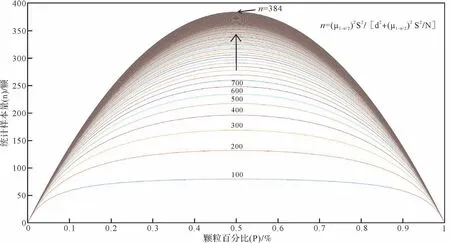
图9 碎屑统计数量参考图不同颜色的曲线为样品碎屑颗粒总数，以100为公差递增；横坐标P为某种颗粒类型的百分含量，纵坐标n为需要统计的数量Fig.9 A reference chart for the number of detritus statisticsThe curves in different colors indicate the total number of grains in the sample,incremented by 100 tolerances;The horizontal coordinate P is the percentage of one type of grain,the ordinate n is the quantity that must be counted

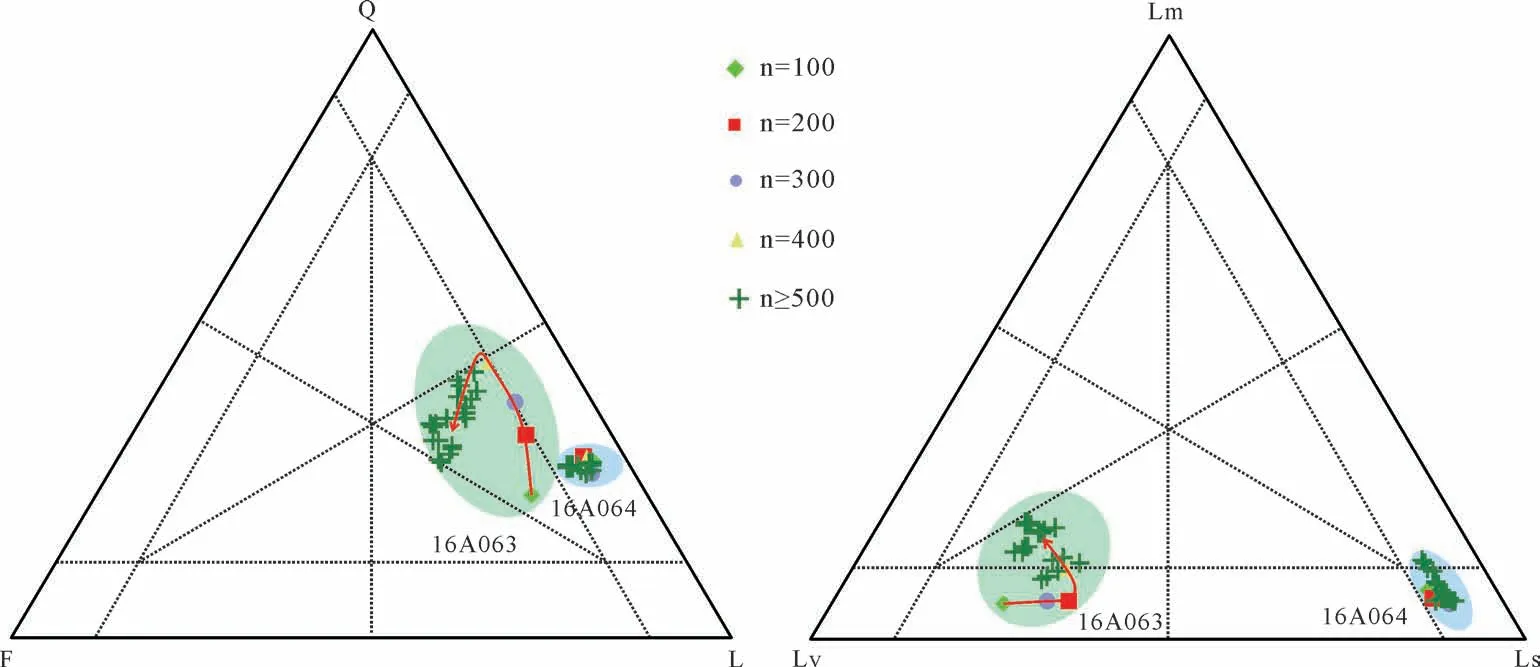
图10 以100 颗为公差递增统计投图Fig.10 Incrementing statistical cast with 100 tolerances

将样品16A063 和16A064 采用颗粒法和面积法统计的统计结果以10 为公差的累积计算，将含量＜5%的颗粒类型与相似参数进行合并，共分为5 类。以最终统计的结果作为标准，将其他各数量的统计结果与该标准求偏差。采用颗粒法统计时，样品16A063 前200 颗的偏差范围最大为-100%～92%，当统计数量达到390 颗时，各类型颗粒偏差范围降低至-30%～6%。样品16A064的统计结果与16A063相似，统计390 颗以上F/Lm/Lv 偏差依然较大，是由于颗粒本身的含量较低导致的（图11a1，a2）。采用面积法统计时，样品16A063 总体偏差范围较大为-100%～158%，是由于样品分选较差所造成的。统计390 颗以上偏差范围减小至-25%～55%，样品16A064的统计结果与16A063相似（图11b1，b2）。

总体而言两个样品在统计390颗以上时，各类型的统计结果与最终统计结果的偏差较小，且较为恒定，个别偏差依然较大的与颗粒含量较低有关。所以理论计算出的384颗与实际统计结果相一致，且该统计数量不受颗粒分选的影响，是一个可行的统计数量。

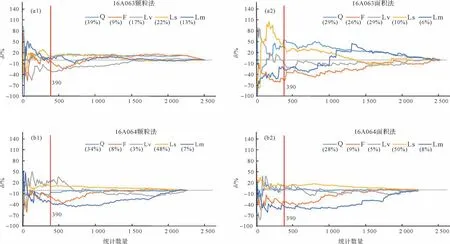
图11 样品16A063 与16A064 同时采用颗粒法和面积法统计结果，以10 为公差累积统计Fig.11 Samples 16A063 and 16A064 using the area method and the point-counting method with tolerance of 10 for cumulative statistics

4 碎屑统计结果的影响因素

4.1 颗粒分选对统计结果的影响

4.1.1 实际样品

两个样品统计结果表明，全颗粒法与全面积法的统计结果有较大的偏差，且样品的分选越差，两种方法统计结果的偏差越大。样品16A063 的分选程度差于样品16A064，颗粒法与面积法统计的偏差前者大于后者（图7c1，c2）。

4.1.2 模拟统计

设置红（r）绿（g）蓝（b）三种不同颜色的球，分为三种不同的粒径组合和含量，分别为：1）等粒径不等面积，粒径比r∶g∶b=4∶4∶4；2）等面积不等粒径，粒径比r∶g∶b=6∶2∶4；3）等面积不等粒径，粒径比r∶g∶b=8∶2∶4。三种不同分选的情况分别采用四种不同的统计方法统计1 900颗以上，将统计结果进行三角投图比较。随着颗粒分选由好到差，四种方法的统计结果的投图分散程度变大（图12）。

说明利用不同的方法对不同的分选程度的样品进行统计时，碎屑颗粒分选越差，由此造成的面积法和颗粒法统计结果的差异性也会更大，所得到的统计结果差异性越大，投点也更分散。

图12 Matlab 模拟颗粒分选对不同方法统计结果的影响Fig.12 Simulation of the different results affected by grain sorting

4.2 颗粒含量对统计结果的影响

4.2.1 实际样品

当某种颗粒类型的面积百分含量或者颗粒百分含量小于样品的10%时，则将该类型颗粒认为是“短板”，既可以是大类，也可以是小类。

采用颗粒法和面积法两种方法所得的统计结果中，含量小于10%的颗粒类型的统计值偏差波动范围变化大，如采用颗粒法统计时样品16A063中的长石颗粒（F），样品16A064 中的F/Lv/Lm（图10a1，a2、表2）；采用面积法统计时样品16A063中的Ls/Lm，样品16A064 中的F/Lv/Lm（图10b1，b2、表2）。其他类型的颗粒也有较大的偏差，但其波动范围较小。

4.2.2 模拟统计

设置等粒径和不等粒径两种情况，以验证在这两种情况下“短板”现象是否均存在。采用Gazzi-Dickinson 法对等粒径颗粒统计，设置绿球的面积百分含量为3%，所得到的统计结果与已知面积求得相对偏差，绿球偏差达10%～20%；对不等粒径统计时，即R（r）∶R（g）∶R（b）=2∶4∶3，颗粒比为n（r）∶n（g）∶n（b）=11∶70∶19，令红球的面积百分含量为10%，含量相对较少的红球和蓝球均有较大的偏差达5%～25%（图13a，b）。

采用Glagolev-Chayes 法统计，设置等粒径，令蓝球的面积百分含量为9%，所得到的统计结果与已知面积求得相对偏差，蓝球的统计含量相对偏差为2%～12%。设置不等粒径即R（r）∶R（g）∶R（b）=8∶2∶4，颗粒比为n（r）∶n（g）∶n（b）=10∶160∶1，设置蓝球的面积百分含量为2%，蓝球统计相对偏差为10%～40%（图13c，d）。

采用Gazzi-Dickinson 法和Glagolev-Chayes 法统计均存在“短板”现象，且含量越低偏差越大。当统计数量少于500颗时，这种现象更为显著。

在展示结果时，要把这些“短板”非常明显的颗粒类型进行重点考虑，如果统计的颗粒为384 颗时，则不能将这些短板的参数直接使用，例如对于Q/F/L三个参数来说，如果L＜10%，则L 不宜再细分，不应进行Ls/Lm/Lv 分析。可与相类似的参数进行合并，以避免“短板现象”的出现。如果重点关注这种短板类型的颗粒，则需要统计更多的数量才能得到较为准确的比例。

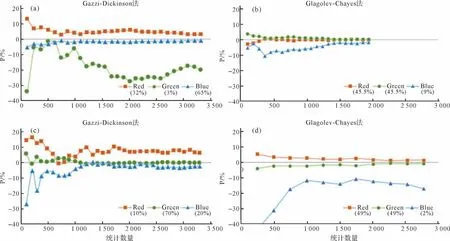
图13 Matlab 模拟Gazzi-Dickinson 法和Glagolev-Chayes 法对不同比例不同粒径的颗粒进行统计时的“短板”现象Fig.13 Simulation of the“short board”phenomenon for Gazzi-Dickinson method and Glagolev-Chayes method