连续时间Markov 工业互联网安全测度研究

李明杰

（安徽财经大学，安徽 蚌埠 233030）

近年来随着信息技术快速的发展，以美国先进制造、德国工业4.0 等为代表。世界上越来越多的国家都在加快推进生产设备数字化、网络化和智能化，全球越来越多的设备接入到互联网。传统相对封闭的工业生产环境与外界互联网连接在一起，也面临着各种各样的网络攻击，网络安全威胁与日俱增。

从2015 年到现在，大型的工业互联网安全事件接连不断，每年都至少有300 起［1］。如2016 年黑客对美国主要的DNS 服务商发动了网络攻击，导致亚马逊、GitHub、Twitter 等大公司的网站出现了长时间无法登陆现象，使许多人觉得整个互联网都瘫痪了；2017 年爆发的“Wanna Cry”总共感染了三十多万台主机，波及了150 个国家，许多企业被迫停产，如雷诺（Renault）和日产（Nissan）等，还有能源、通信等行业都遭受了巨大的损失；2018年GlobeImposter 勒索病毒入侵山东省房地产注册系统，导致数据丢失、无法显示和无法存储等诸多问题，十多个城市发布了终止房地产登记的通知；2019 年，委内瑞拉的电力系统遭到网络攻击，导致委内瑞拉首都加拉加斯等多个城市的灯光突然熄灭，还有一些地区的网络通信和供水系统出现中断。由此可见，工业互联网络关系到工业、能源、交通以及市政等各个领域。一旦出现安全问题，将会对社会的各个方面带来严重的灾难，因此工业互联网的安全已成为阻碍社会发展的关键问题［2］。

1 工业互联网系统安全测度分析

工业互联网是一种特殊的网络，目前大部分工业生产都逐渐融入其中。工业互联网是由许多工业生产设备和网络设备共同构成的，其中工作内容不同的网络节点都具有不同的功能。工业互联网中最为核心的关键基础设施具有一定的实时性和可持续性。这就要求对工业互联网安全性进行测度的时候必须具有一定的可度量性。必须对整个网络的多个属性进行合理的分类整合，最终得到一个合理的、准确的、可靠的工业互联网安全测度方法。工业互联网的运行是动态的，如何确保在工业互联网络运行中分析测度工业互联网的安全，最终获取到准确有效的数据是一个难点。

工业互联网安全性测度是在综合多种影响系统网络安全的因素基础上，通过科学合理的方法或模型，量化计算得到整个网络系统整体上的安全风险状况。相比于传统的静态评估方法，基于马尔科夫模型的安全测度方法，可以刻画出工业互联网系统中每个节点的安全风险状态。该模型高效实时，能够时刻反映整个系统的网络安全态势。对整个系统安全风险的计算方式，传统的方法是采用简单的各个节点风险直接相加，无法区分不同节点在整个系统结构中的位置和作用，并且节点和状态过多的时候会发生“状态爆炸”的情况，计算繁琐，效率较低。针对上述方法的不足，本文通过自上而下的方式先充分了解整个工业互联网的结构调整，构建结构方程，然后通过自下而上逐步求解子系统安全风险值，利用生成函数导出上层直至整个系统的安全风险值。该方法不仅深刻揭示了整个系统的结构特征，还降低了计算的复杂度，解决了由于系统组件和状态过多引起的“状态爆炸”问题［3］。

2 基于连续时间Markov 模型测度方法

工业互联网存在的外部网络攻击威胁以及系统内部的自身脆弱性导致的设备故障等是网络系统产生安全风险的关键因素。因此，要对工业互联网系统进行安全性测度就需要收集整个网络系统的状态信息。确保安全分析的内容涵盖整个工业互联网系统［4］，依据连续时间Markov 理论建立安全测度模型，分析计算系统的安全状况，给出相应的建议和修复措施，优化网络系统结构。具体流程如下：

（1）通过入侵检测系统对外部网络攻击进行检测扫描收集数据，对于内部系统自身安全通过收集历史数据并诊断验证一段时间各个组件出现的故障概率和故障类型。

（2）确定状态表，并依照一定的标准来进行状态划分。

（3）生成马氏链的状态表，并对所有节点的状态转移情况进行统计分析，并生成状态转移强度矩阵P［5］。

（4）根据系统中节点所处的位置与系统结构构建结构方程，通过生成函数z 变换求得整个系统的状态概率，最终求解系统的安全风险值。具体内容如图1 所示：

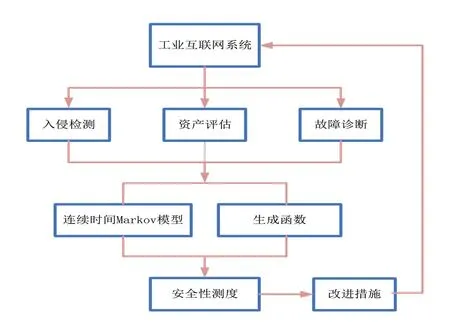
图1 工业互联网系统安全性测度流程

3 建模与风险值计算

3.1 连续时间Markov 模型

连续时间Markov 模型是一种随机模型，可以表示为一个3 元组（S，P，ð ），在将其应用于工业互联网安全性测度，本文对模型的各个参数进行定义，为便于描述，关于系统中的各个组件设备称为一个节点［6］。

（1）S 为状态空间集合，S={S1，S2，…，S N}，其中N 表示安全状态的总数，系统中的节点在不同的安全事件（如病毒传播、黑客攻击中会处于不同的安全状态。用随机过程{X t,t≥ 0}来表示，其中Xt表示节点在时刻t的安全状态。通过对历史数据的分析，本文将目标节点的安全状态集合空间划分为四个状态［7］。如表1 所示，当节点的状态分别用H，C，R，F 表示，那么状态集合S={H，C，R，F}。

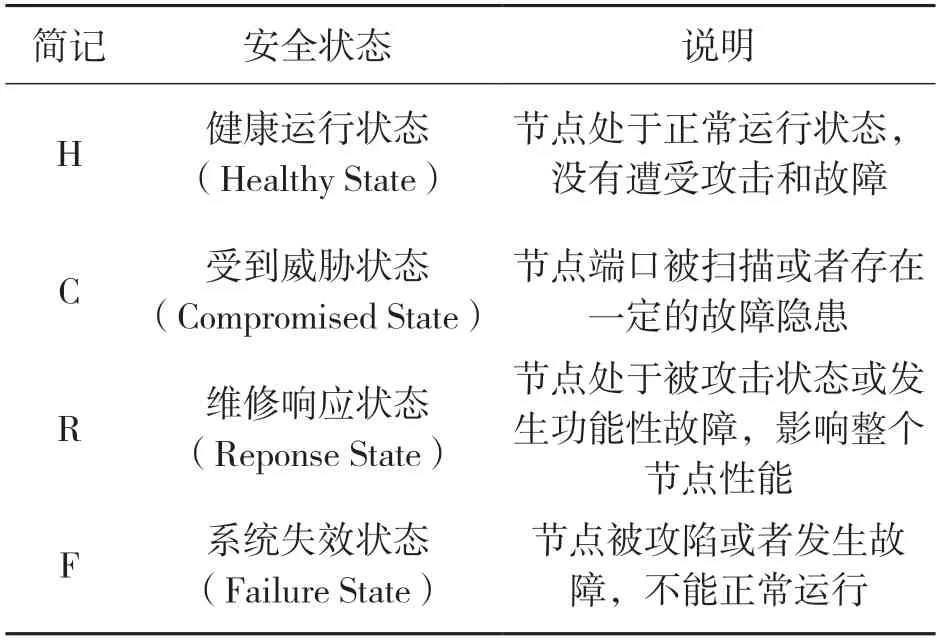
表1 节点安全状态集合

（2）P 为状态转移概率矩阵。P=［pij］，p ij=P（Xt+At=sj|Xt=si），1≤i，j≤N。且存在对于任意i，1≤i≤N，满足(t,t+Δt)=1,O≤pij(t,t+Δt) ≤ 1，1≤j≤N。由于整个系统中存在一定的防御措施，所以当节点遭遇不同的安全事件而出现危害的时候，系统中会做出相应的防御措施从而降低这些安全事件对节点的威胁程度，因此节点的安全状态可以相互转移，这种转移过程都存在一定的概率关系，这就符合马尔科夫特性，安全状态转换如图2 所示［8］。

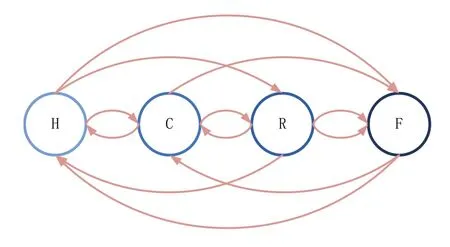
图2 节点安全状态转换图

关于计算状态转移强度矩阵P，矩阵中每一个元素pij对应的是节点从安全状态i 转移到安全状态j 的概率。一般Markov 链在进行预测时候是通过确定一步转移概率矩阵P，然后结合当前状态计算Markov 链在达到稳态时的状态概率矩阵。传统的Markov 模型是假设状态概率转移矩阵P 在达到稳态的情况。在现实中状态转移概率不容易求得，因此需要求得节点的转移率pij，通过转移率来求得节点在未来时间处在不同状态的概率，在进行数据处理计算的时候采用频率近似概率的原理，，其中nij表示一个节点从安全状态i 转移到安全状态j 的样本数。如节点1 在一年内从健康运行状态转移到受到威胁状态的次数是5，那么转移率PHC=5 次/年。如果有新的检测数据加入的时候，将历史统计数据和当前新加入的数据一起统计，计算得到状态转移强度矩阵，使得最后安全值的计算更加时效。状态转移强度矩阵如下：

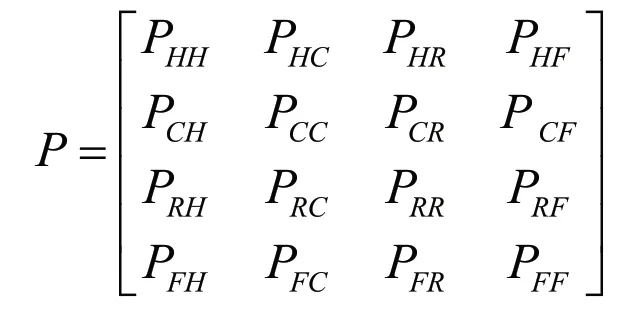
（3）π={π1，π1…πn}表示系统中节点在初始时刻的状态概率分布。πi=P（X0=si），1≤i≤N表示在初始时刻t=0 节点处于状态si的概率，且满足。连续时间Markov 链的未来的概率行为完全是由初始的概率向量π（0）和转移概率矩阵Pij来决定的。

3.2 系统安全风险值的计算

3.2.1 节点安全值计算［9］

首先针对节点所处的安全状态定义节点的安全风险向量C={c1,c1,…cN}，与节点所处的安全状态向量集合相对应，表示节点在每一个安全状态的风险值。与上文所描述的四种安全状态相对应，设定安全风险向量C={1、10、20、100}，表示节点在状态H、C、R、F 下的安全值分别为1、10、20、100。可以认为一个节点的安全值在1～5 之间表示该节点处于一个安全的状态，安全值在5～15 之间表示该节点可能被外部网络扫描端口或者自身长期运行可能出现硬件故障，安全值在15～50 之间，表示该节点已经遭受了网络攻击或者自身出现了轻微的硬件故障，安全值超过50 表示该节点已经被外部网络或者自身硬件故障导致不能正常运行从而影响整个系统的工作。

对系统中的任意节点k，将其在时刻t 的安全值计作Rk（t），依据节点在时刻t 的状态概率分布，以及主机安全风险向量C=（c1,c1,…c1N），求得安全值：

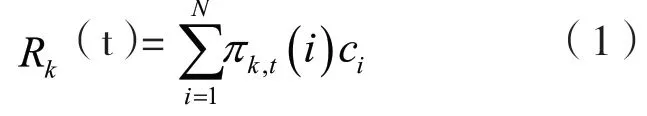
3.2.2 系统安全值计算

假设系统中有L 个节点，分别为1、2、…L，相应的节点安全值计作Rl（t），1≤l≤L。传统的系统安全值的计算方式是各个节点安全值直接相加求和，然后计算算数平均值，最终得到整个系统在t 时刻的平均安全风险值［10］。这样求得系统的安全风险值没有考虑系统中各个节点在系统中所起的作用不同和相互之间的结构关系。

为解决上述问题，依据通用生产函数的理论，首先充分了解分析整个工业互联网系统的结构特征，构建结构方程。根据生产算子Ωf求出代表整个系统的联合生成函数f{L1，L2,…Ll}，1≤l≤L。定义整个系统的安全状态变化的随机变量函数Y=f{L1，L2,…Ll}，通过每个节点所代表的离散型随机变量L1，L2,…Ll中的Z 变化多项式可以确定代表系统的随机变量函数Y=f{L1，L2,…Ll}。

4 实验仿真

4.1 实验环境

为验证提出的工业互联网安全度量方法的有效性和可行性。搭建实验环境，具体的系统网络拓扑结构如图3。系统内部传输由三个交换机组成，分别为组件1、组件2 和组件3，通过防火墙可以与外网互联。

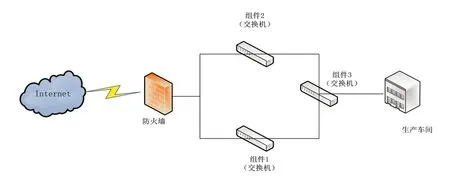
图3 网络系统拓扑图

首先对历史数据进行分析归纳，三个交换机都具有三种安全状态，分别对应的安全风险向量C={0，10，50}，安全向量越小表示系统的安全风险越低，系统运行过程中组件对应的安全风险值分别表示为：

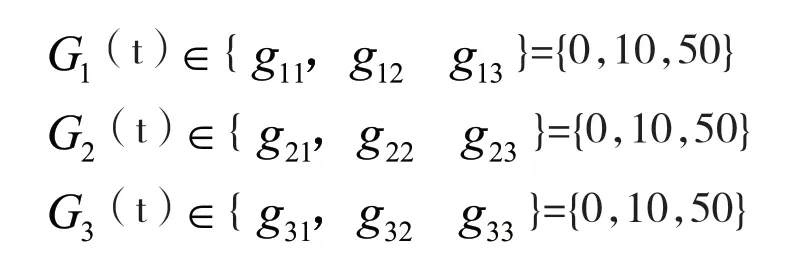
组件的安全状态转换如图 4，λ表示组件从安全性较高的状态转移到安全性较差的状态，μ表示组件从安全性较差的状态转移到安全性较高的状态。λ和μ分别表示状态之间的转移率。

4.2 实验数据求解过程

首先根据检测到的历史数据通过分析研究得到各个组件状态之间转移率，转移率以次/月为单位，求得各个组件的状态转移率矩阵分别为：

组件1：

由网络系统拓扑图可知，三个组件之间的结构是组件1 和组件2 并联，然后再和组件3 串联，因此整个系统的结构函数为：

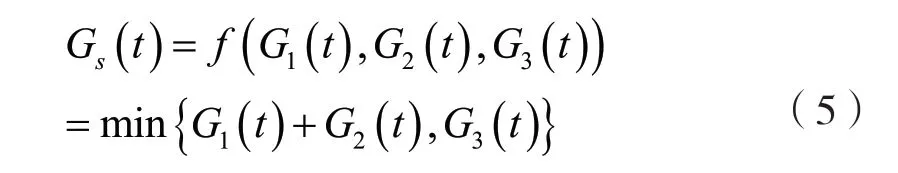
根据组件之间的状态转移率，根据Markov 理论为每个交换机组件构建微分方程求解组件在任意时刻t 处在各个状态的概率P：

组件1：

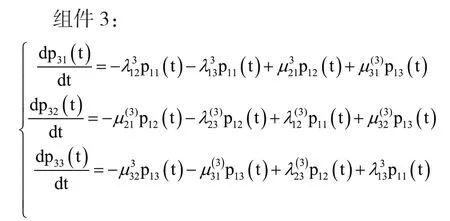
初始条件是：p31(0)=1，p32(0)=0，p33(0)=0

通过MATLAB 软件编程求解上述微分方程组，得到组件1 在各个安全状态的概率表达式如下所示：

因此可以得到每个组件在时刻t 的安全状态概率分别为：

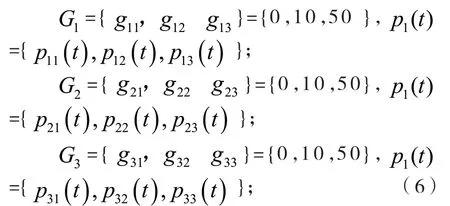
求解整个系统的安全风险具体数值，以组件的安全状态概率分布根据系统组件结构来构建通用生成函数，得到整个系统的状态概率分布，最后系统的安全风险数值R（t）=。列出每个组件的通用生产函数分别为：

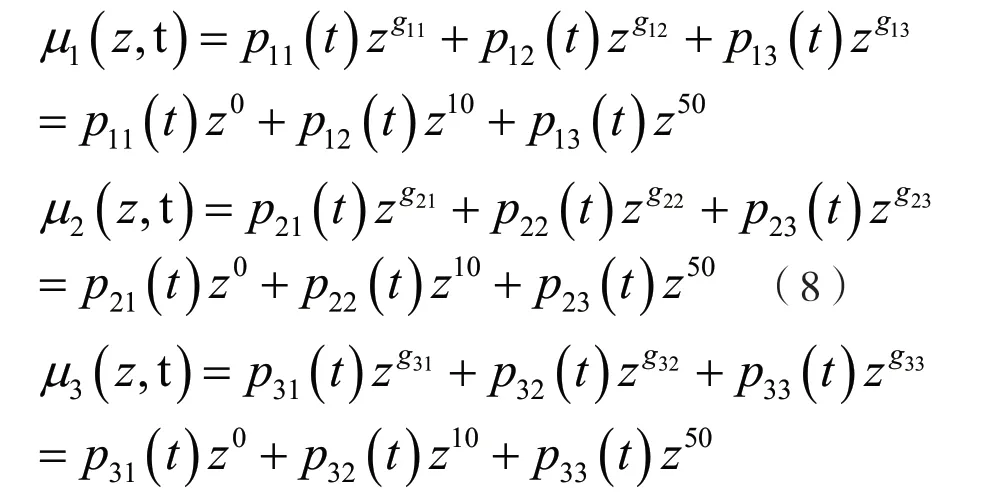
由系统的拓扑结构图可知，组件1 和组件2是并联结构，安全风险值可以取两个组件的最小值，组合算子为：，并联以后再和组件3 串联起来，安全风险值要相加，组合算子为，因此整个系统的通用生产函数为：

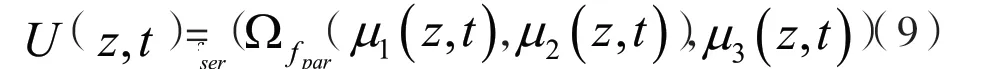
设组件1 和组件2 并联结构的通用生产函数为U12(z,t)：

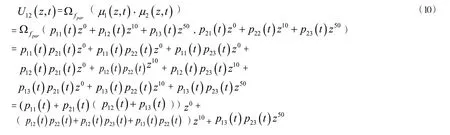
因此整个系统的通用生产函数为：

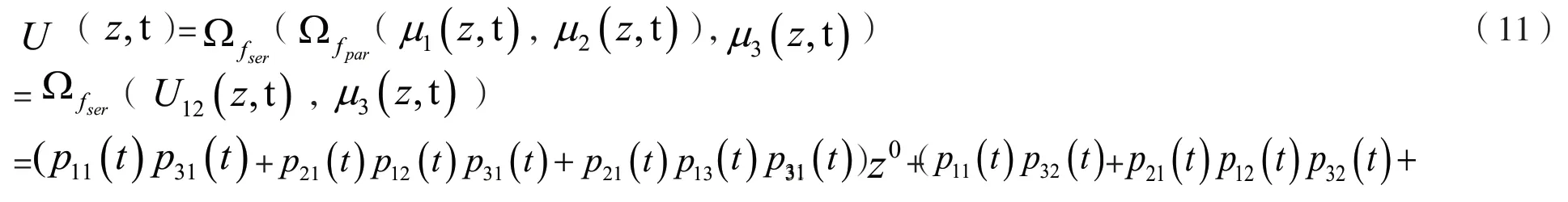
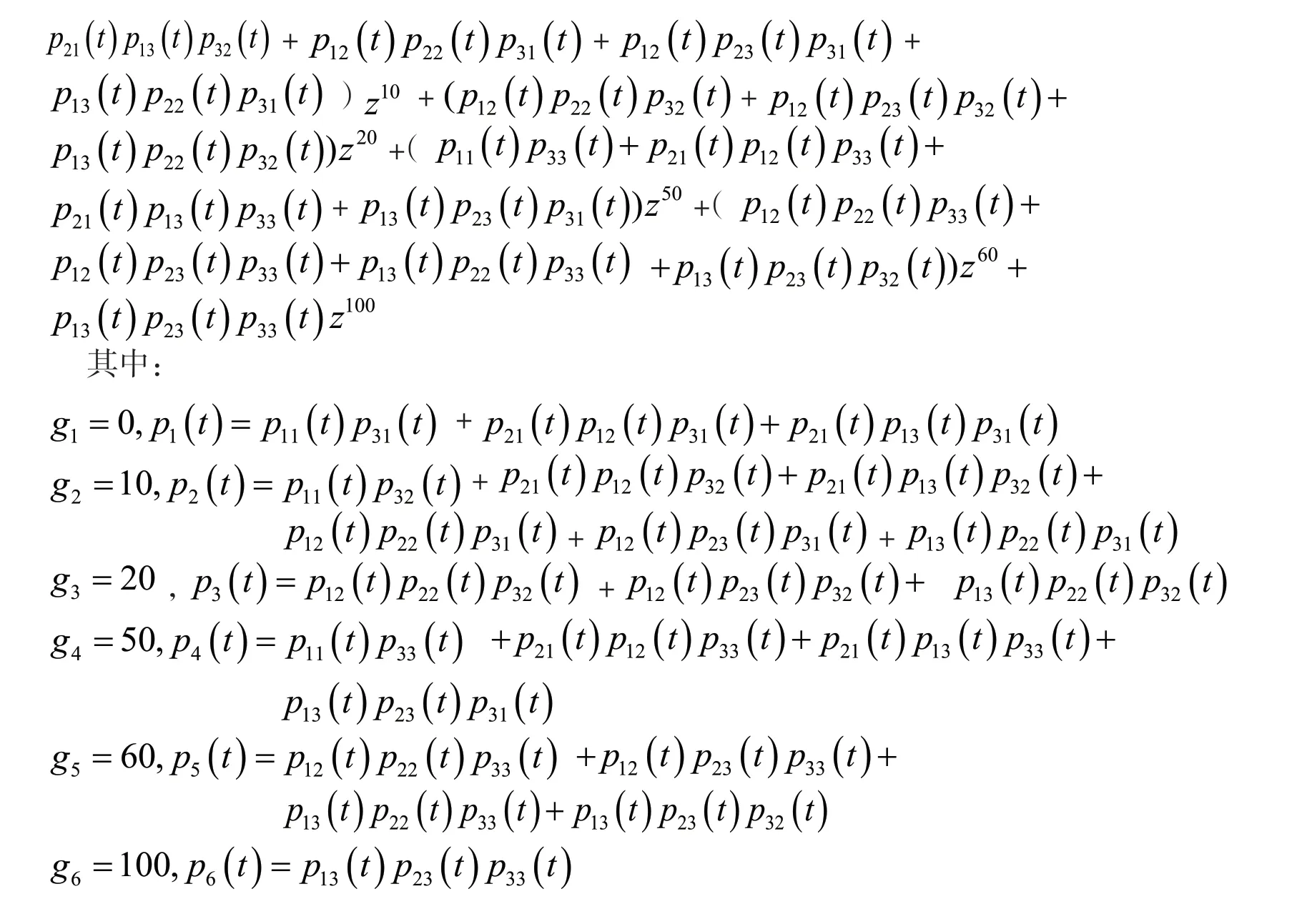
通过MATLAB 软件编程计算可以得到整个系统处于6 种状态的概率变化情况。

计算得到系统处于6 种状态的概率变化如图5 所示：

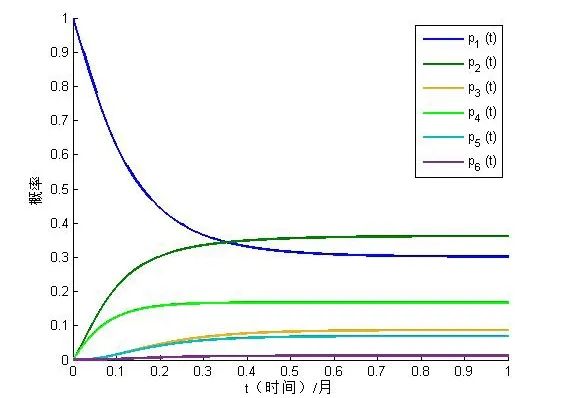
图5 系统状态概率变化图

由图5 可知，处于稳定状态以后，系统在各个状态的概率分别为：

用集合表示为：

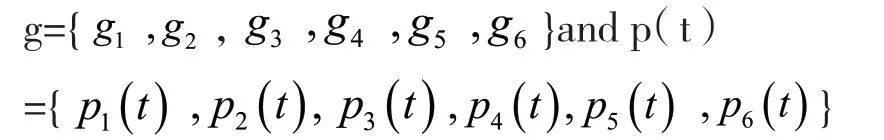
最后计算整个系统的安全风险值：

通过MATLAB 编程得到整个系统的安全性能变化情况如图6 所示：

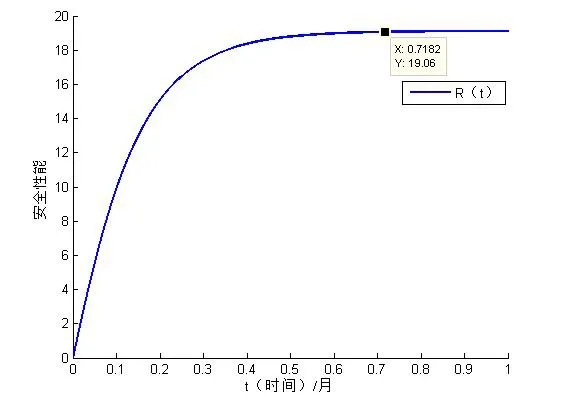
图6 系统风险值变化图

通过图6 可知，系统在未来一个月内，风险值逐渐上升，到大约21 天趋于稳定，安全性能为19.06。这样系统的管理人员可以根据风险值的变化来确定系统什么时段的安全风险急剧增加，可以在这个时刻来对系统进行安全维护，保证整个网络系统的风险处于一个较低的水平，这样就可以时刻保持工业生产的正常运行。

5 结语

工业互联网的快速发展带动了社会经济增长与时代的进步，与此同时工业互联网打破了传统工业生产系统相对可封闭的环境，各个控制系统和生产设备与外界互联网相连，使其不可避免地面临传统的网络威胁，各种工业安全事件呈现爆发式的增长，对社会造成了恶劣的影响。工业互联网的安全问题已成为当下亟待解决的问题。本文基于连续时间Markov 模型对工业互联网安全量化评估领域进行了研究，提出了基于连续时间Markov 模型对工业互联网安全性进行度量，并引入通用生成函数降低了模型计算的复杂度，建立了完善的工业互联网安全性测度模型。