基于同步失效准则的新型双吊点取料臂研究1)
2022-08-19刚宪约
孟 朋 刘 梦 于 明 刚宪约
(山东理工大学交通与车辆工程学院,山东淄博 255000)
近年来,随着我国经济的蓬勃发展,散料货物运输量迅猛增长,半门式刮板取料机作为散料装卸重要设备之一,已广泛应用于电力、建材、化工、矿山、码头、煤炭等众多国民经济行业[1]。目前市场上半门式刮板取料机结构形式大都如图1所示,其中取料臂的尾端与固定端梁铰接,另一侧通过卷扬提升系统吊挂在半门架下,与刮板、链条、链轮、驱动装置等部件共同完成取料作业[2-3]。对于中小型的刮板取料机,取料臂跨距小、自重轻,这种单吊点取料臂尚能满足结构的安全性能要求。但随着取料机大型化的发展趋势,取料臂的跨距越来越大[4],再采用单吊点取料臂可能会造成部分结构应力集中或结构变形不合理等情况,增加取料臂的安全隐患。

图1 半门式刮板取料机Fig.1 Semi-portal scraper reclaimer
为了改善单吊点取料臂的不足,本文提出一种等力双吊点取料臂,并对其进行力学性能分析,研究双吊点悬吊位置对取料臂结构强度和刚度的影响。基于同步失效准则与等弯矩峰值设计原理建立等力双吊点取料臂最优悬吊位置设计模型,推导最优悬吊位置及最优位置系数。最后结合具体实例,对比验证等力双吊点比单吊点取料臂的应力分布更优。
1 等力双吊点取料臂力学性能分析
如图2所示,在单吊点取料臂的基础上,于半门架和取料臂之间增加一套悬吊装置及滑轮组。将取料臂吊挂在半门架下(图中省略刮板、链条等零部件),并保证取料臂两悬吊位置上钢丝绳对其拉力相同。与旧方案相比,新方案增加的制造成本与操作难度并不高,大大增加了方案的可行性。
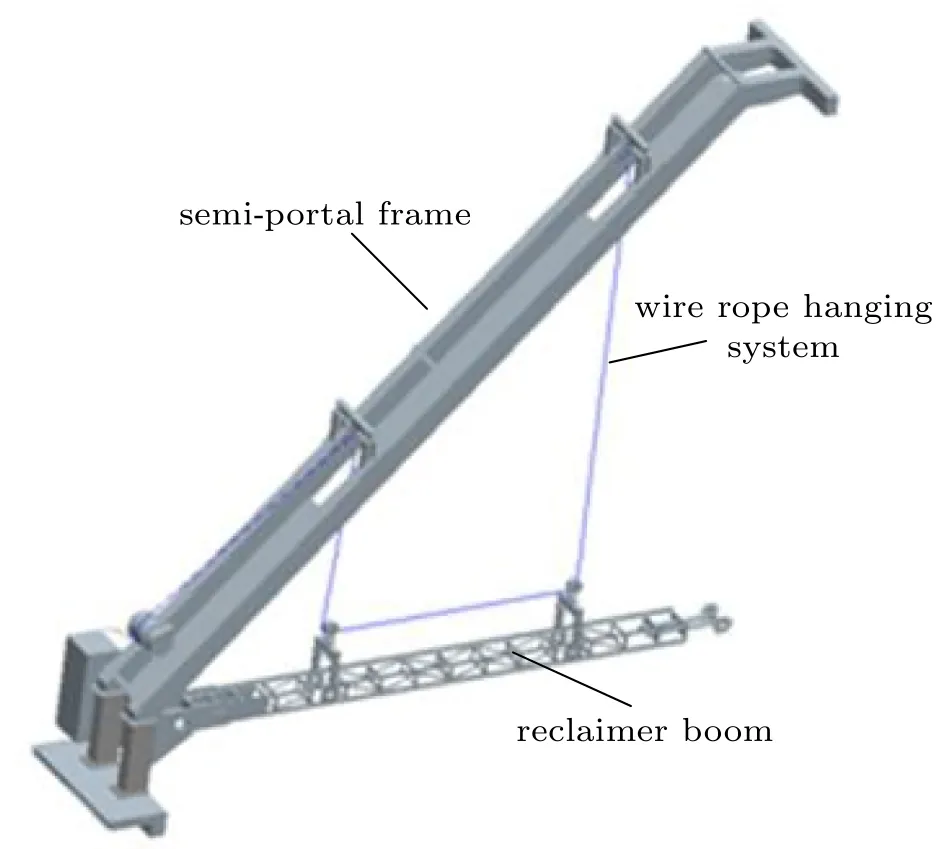
图2 桁架式双悬吊点取料机结构示意图Fig.2 Truss-type dual hanging point scraper reclaimer structure diagram
取料臂在竖直方向上主要承受自身结构重力、部分物料重力、销轴的约束力及钢丝绳的拉力等[5]。大型取料机取料臂的跨度在20 m以上,长度远远大于宽度,可以近似等效为一端铰接、双点悬吊的细长梁结构,如图3所示。图中,OC代表整根取料臂,长度为L;O点为取料臂尾端的销轴中心;靠近销轴中心O的A点为取料臂的第一个悬吊点,距销轴中心的距离为l1;B点为取料臂的第二个悬吊点,距销轴中心的距离为l2;A和B两悬吊位置上钢丝绳在竖直方向的拉力均为F;q代表由取料臂自重和部分物料重力等效成的均布载荷。
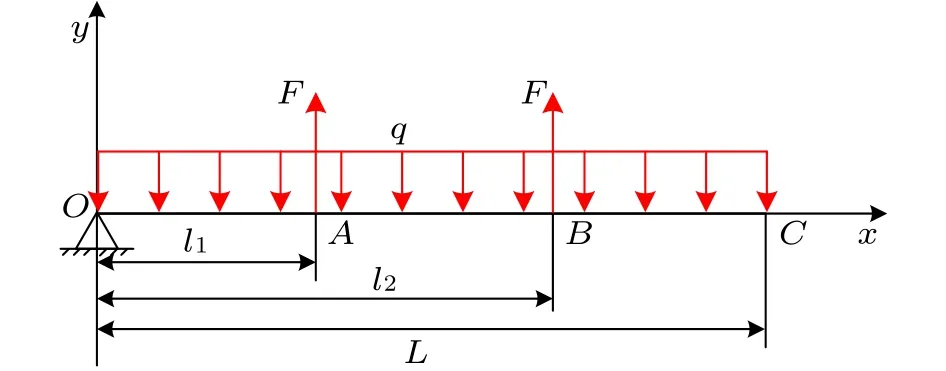
图3 等力双悬吊点式取料臂受力分析图Fig.3 Forces applied on a reclaiming boom with dual equal-force hanging points
根据力与力矩平衡关系建立方程
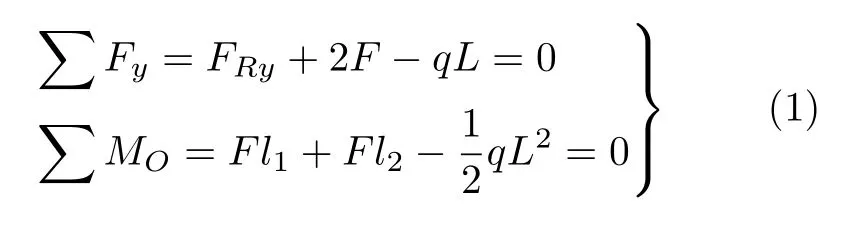
式中,Fy代表力系在竖直方向上的分力,FRy代表取料臂尾端O点销轴在竖直方向上的支反力,MO代表力系对点O的力矩。
由平衡方程求得销轴在竖直方向上的支反力FRy和取料臂两个悬吊位置上钢丝绳的拉力F分别为
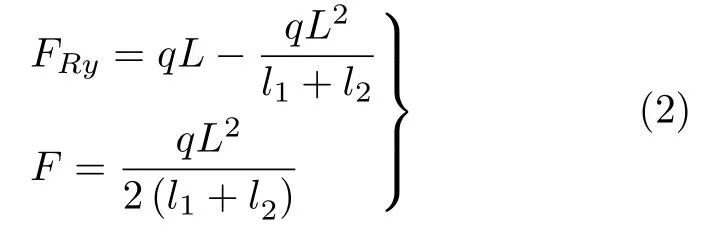
正常情况下,取料臂末端销轴处的竖直约束力FRy为正(向上),因此有l1+l2>L。
等力双吊点取料臂的弯矩方程为
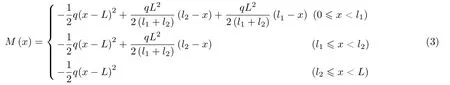
式中,M表示弯矩。
根据式(3)绘制出等力双吊点取料臂的弯矩示意图,如图4所示。图中,MP1,MP2,MP3和MP4分别为等力双吊点取料臂弯矩的四个峰值,lP1,lP2,lP3和lP4分别为四个弯矩峰值所对应的截面位置,其中lP1和lP2正好对应两个悬吊位置,即lP1=l1,lP2=l2。
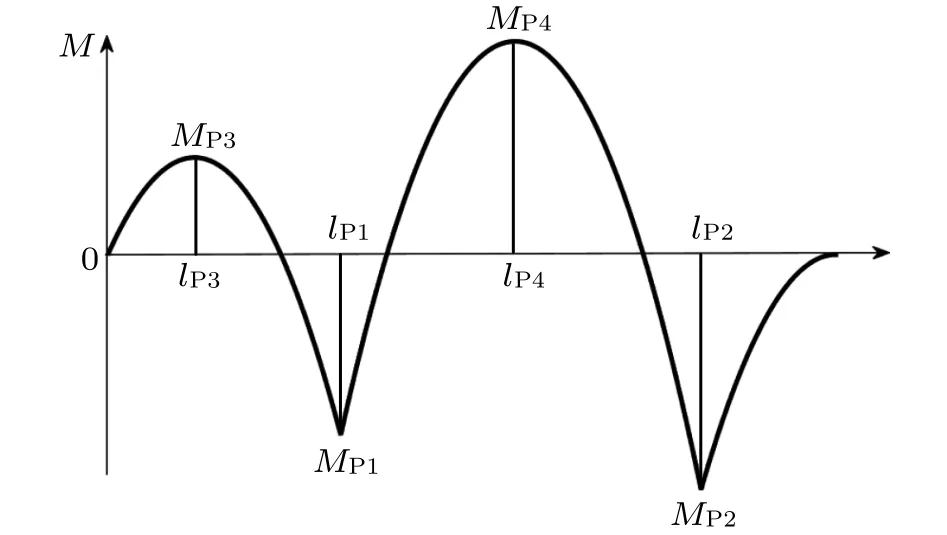
图4 等力双吊点取料臂弯矩示意图Fig.4 Bending moment of reclaiming boom with dual equal-force hanging points
根据数学极值原理,结合取料臂的弯矩示意图,将式(3)对坐标x求导并令导数为零,获得弯矩峰值MP3和MP4所对应的截面位置。
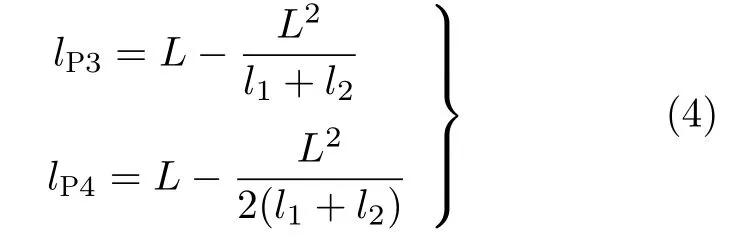
将四个弯矩峰值所对应的截面位置代入式(3),即可求解出弯矩峰值MP1,MP2,MP3和MP4的大小
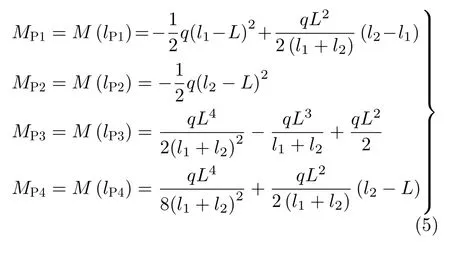
将等力双吊点取料臂近似看为等截面梁结构,则取料臂在四个弯矩峰值的位置处会产生四个相对应的弯曲正应力峰值。根据等力双吊点取料臂的弯矩公式及示意图可知,当取料臂的长度L和均布载荷q一定时,取料臂的弯矩分布情况仅与取料臂的两个悬吊位置l1和l2有关。
2 等力双吊点取料臂最优悬吊位置设计模型
对于等截面梁结构的支点或悬吊点位置的优化设计,采用同步失效准则提供的设计公式方便有效。同步失效准则,就是构件的各个组成部分同时抵达许用强度或失稳安全限度,由此得出一组联立方程,其解析解提供了构件的最佳优化设计尺寸[6-7]。本文基于同步失效准则,对取料臂悬吊位置进行优化设计,采用等弯矩峰值设计原理[8],选取最优的悬吊位置,令取料臂的各个弯矩峰值的绝对值相等,即应力峰值绝对值相等,从而使得整根取料臂的弯矩和应力分布最优,达到构件各组成部分同时抵达许用强度或失稳安全限度的目的。建立双吊点取料臂最优悬吊位置的设计方程
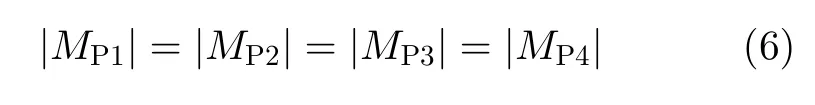
其中,比较|MP1|和|MP2|的大小,建立其关系表达式
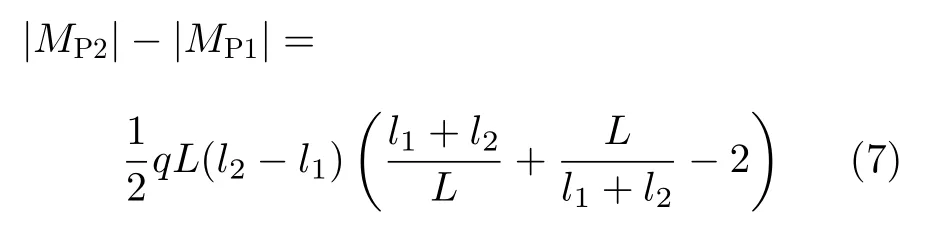
由上文可知l2大于l1,因此|MP2|>|MP1|始终成立。等力双吊点取料臂最优悬吊位置的设计方程可以简化为
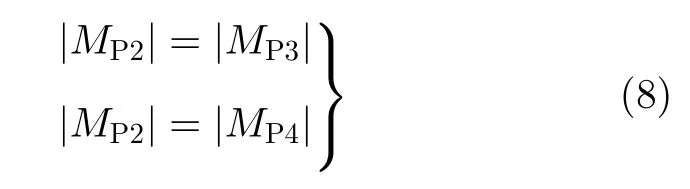
即
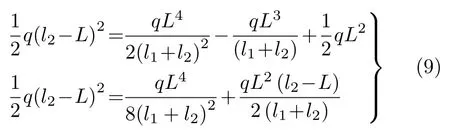
求解方程(9)获得等力双吊点取料臂的最优悬吊位置l1*和l2*为
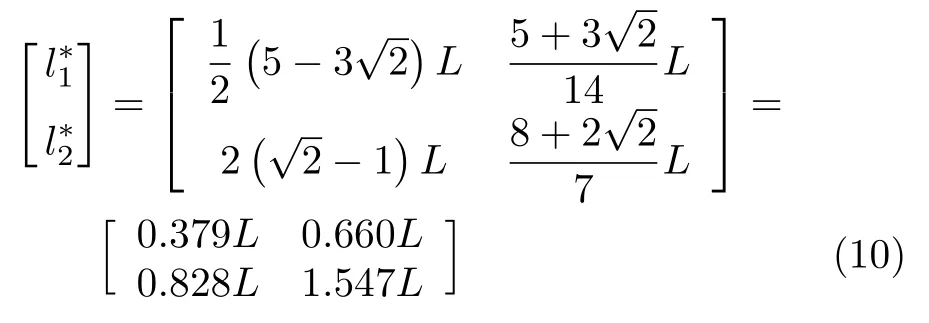
根据实际情况,取料臂的悬吊位置l1和l2都不能大于取料臂的长度L,所以仅剩一组最优解

令μ1= 0.379,μ2= 0.828为等力双吊点取料臂的最优悬吊位置系数,该系数与取料臂的实际长度无关。
将式(11)中最优悬吊位置l1*和l2*代入式(5),可以求解出等力双吊点取料臂在最优悬吊位置下的各个弯矩峰值分别为
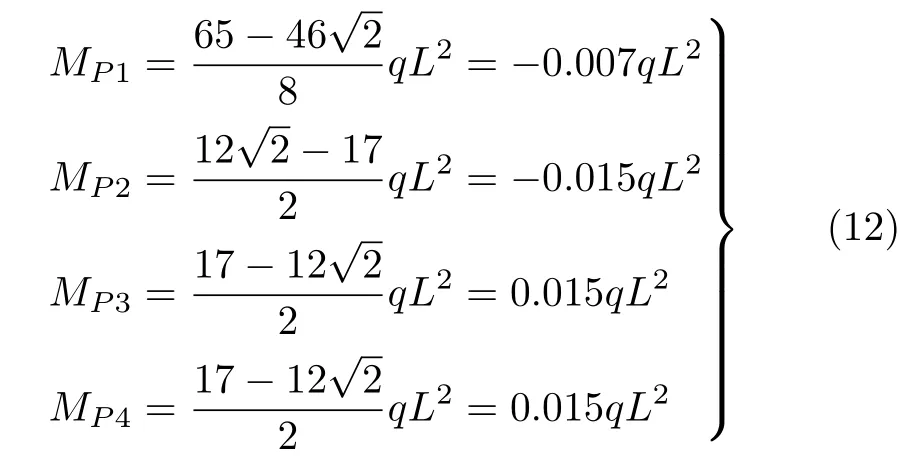
相同规模下的单吊点取料臂[9],其悬吊点的最优位置为0.707L,计算出的最大弯矩峰值为0.043qL2。等力双吊点取料臂在最优悬吊位置情况下的最大弯矩峰值为0.015qL2,比单悬吊点取料臂小65.12%。
结合式(12),令在最优双悬吊位置下取料臂最大弯矩峰值的绝对值为1,绘制出等力双吊点取料臂最大弯矩峰值绝对值随双悬吊点位置变化的关系示意图,如图5所示。由上文可知悬吊位置l1和l2应满足

根据式(13),图5中有效区域显示为三角形。
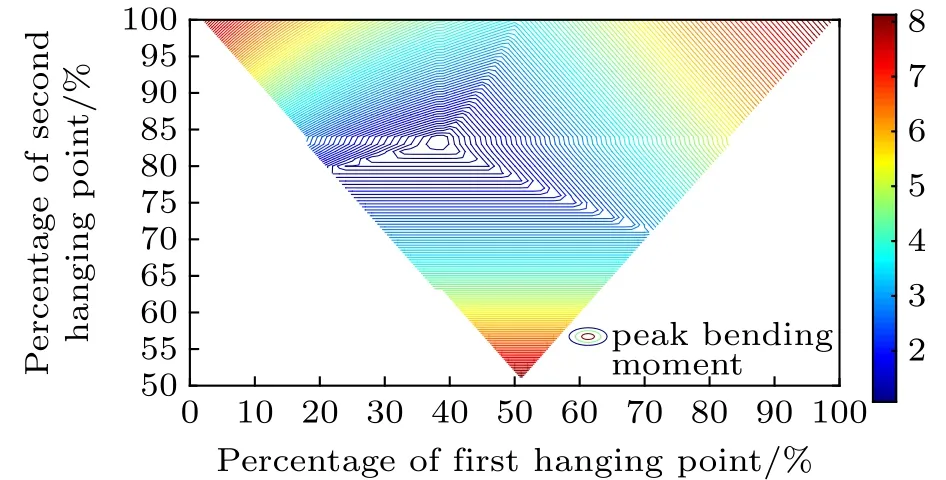
图5 等值线图Fig.5 Contour plot
3 实例对比分析
3.1 静力学分析
某型号半门式刮板取料机的桁架式取料臂总长20 935 mm,取料臂臂架结构总重为2 776 kg,链条、链轮、刮板等其他零部件的重量及部分物料的重量共计1 792 kg,由取料臂自重和部分物料重力转换成的均布载荷为2.182 N/mm。经计算得单吊点取料臂的最优悬吊位置是14 801 mm;等力双吊点取料臂的最优悬吊位置为l1= 7 934 mm,l2= 17 334 mm。根据取料臂的弯矩方程绘制出两种悬吊方式的弯矩图,如图6所示。由图6可以直观地看出,相同规模的等力双吊点取料臂最大弯矩远小于单吊点取料臂最大弯矩且分布更加合理。
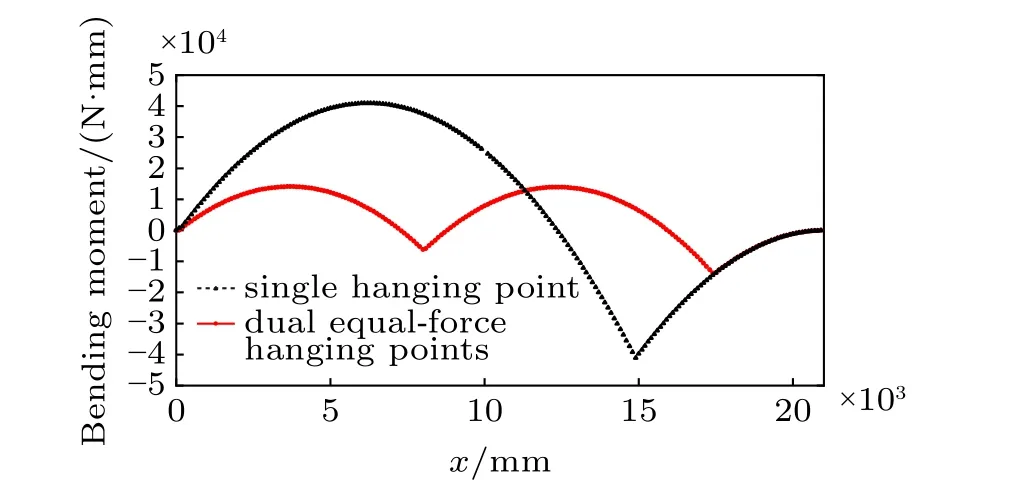
图6 两取料臂弯矩图Fig.6 Bending moment of two reclaiming booms
针对两种悬吊方案的取料臂,在有限元分析软件ABAQUS 中分别建立最优单吊点取料臂、最优等力双吊点取料臂有限元模型,并进行相同工况的有限元分析。材料为Q235,弹性模量E=210 GPa,半门式刮板取料机整体结构的安全系数取n= 1.5,材料许用应力为[σ] = 157 MPa。取料臂整体受弯矩影响,但局部变形不一定是弯曲变形,即取料臂最大应力主要受弯矩影响但并不与弯矩完全成正比[10]。本文主要研究的是取料臂悬吊位置对取料臂整体的影响,因此在分析有限元计算结果时,忽略掉内部斜撑焊接部位以及梁单元与板壳单元连接部位的复杂应力,主要选取取料臂架的四根主纵梁作为目标进行分析。计算结果如图7和图8所示,图中Mises等效应力单位为MPa,位移单位为mm。
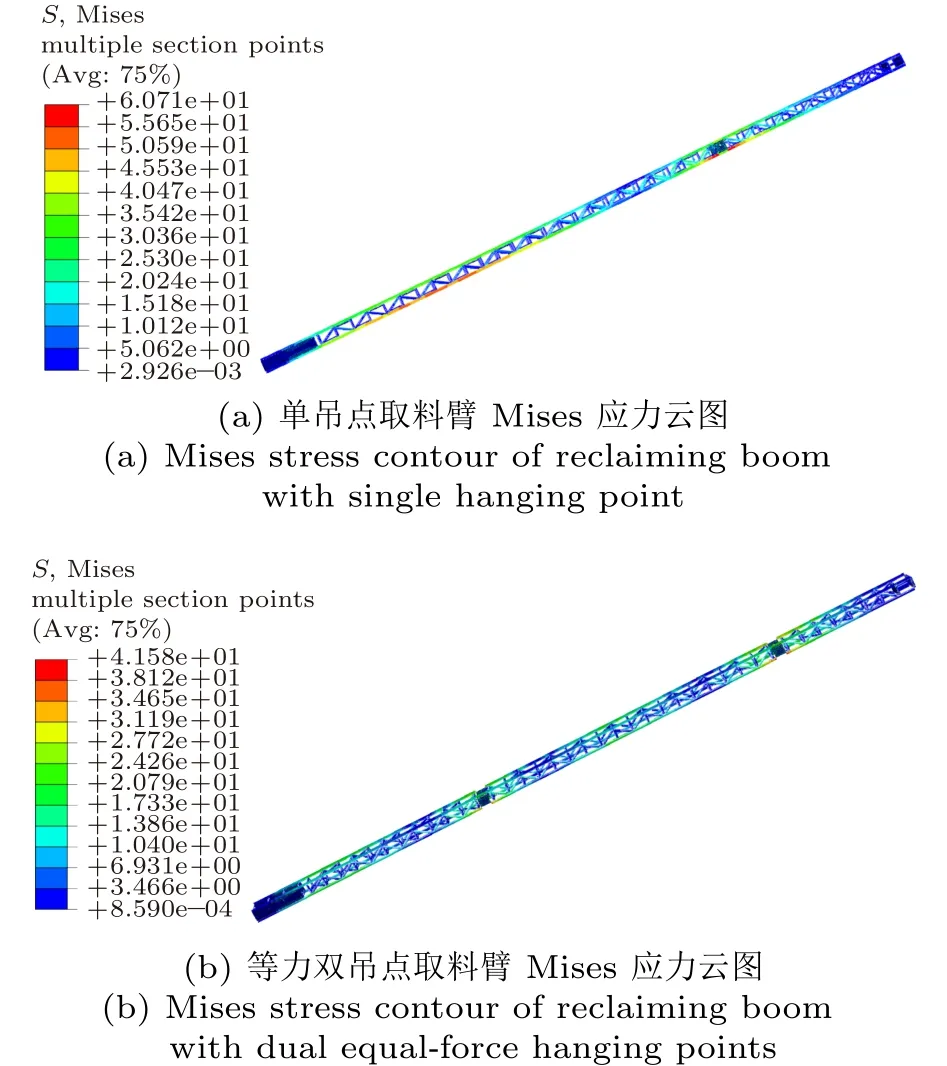
图7 两取料臂Mises应力云图Fig.7 Mises stress contour of two reclaiming booms
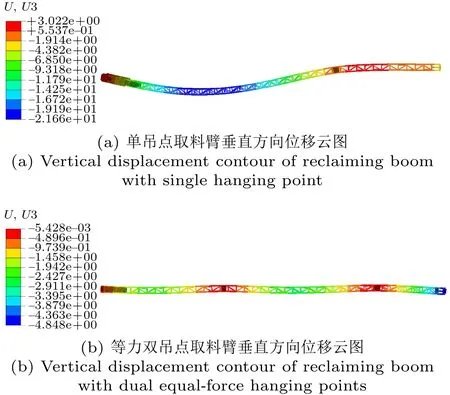
图8 两取料臂垂直方向位移云图Fig.8 Vertical displacement contour of two reclaiming booms
将有限元计算结果汇总到表1中,表中峰值位置均为距离取料臂轴销中心的长度。最优悬吊位置下的等力双吊点取料臂比单吊点取料臂的应力峰值减小三分之一左右且应力分布更优。单吊点取料臂垂直方向位移最大峰值为21.66 mm,等力双吊点取料臂垂直方向位移最大峰值为4.85 mm,优化效果十分明显。最大应力位置与理论计算结果十分接近,虽然应力峰值由于斜撑等结构产生了一定影响,但应力优化效果十分明显,可以证明等力双吊点最优悬吊位置设计模型及所求得最优悬吊位置系数的合理性。

表1 取料臂有限元计算结果Table 1 The computer aided engineering results of reclaiming boom
3.2 突然启动瞬态响应分析
沿用静力学的模型,取料机工作时突然提起取料臂使其从静止瞬间加速至最大速度,并保持最大速度继续提升,模拟实际工作中取料臂受到冲击情况。已知电机最大速度为6 m/min。最大应力点的应力随时间变化的曲线如图9所示。
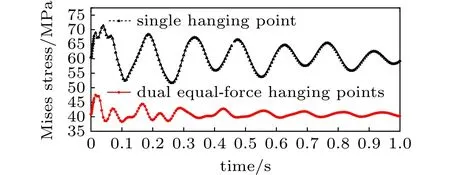
图9 应力变化曲线Fig.9 Stress curve
两取料臂最大应力点分别出现在14 450 mm处与17 730 mm处,最大应力点位置与静力学结果相对应。两取料臂最大应力值分别为71.3 MPa与47.4 MPa,最大应力处于许用应力范围内。与单吊点取料臂最大应力相比,双吊点取料臂的最大应力减小了三分之一左右,应力分布更合理。
4 结论
本文针对传统单吊点取料臂应力分布不合理等问题,基于同步失效准则,提出了一种等力双吊点取料臂的悬吊方案,通过理论推导与实例分析得到以下结论。
(1)当取料臂可以近似看作等截面细长梁时,求解出最优悬吊位置系数为0.379和0.828。该系数与取料臂的实际长度无关,因此可以适用于各种等力双吊点结构。该方案具有良好的通用性。
(2)对比优化前后的分析结果发现,优化后取料臂的应力及变形分布更加均匀合理,安全性更高,证明了其有效性。
(3)新方案仅仅增加了一套悬吊装置与滑轮组,制造成本与操作难度没有增加太多,具有很高的可实现性。
(4)通过对等力双吊点取料臂悬吊位置的优化研究,不仅能够改善取料臂的受力情况,提高设备安全可靠性,还可为同类型悬吊结构的设计优化提供新的改进思路。