基于频率安全约束与临界惯量计算的分时段限制风电出力方法
2022-08-19李世春田冰杰李惠子黄森焰徐松林
李世春,田冰杰,李惠子,罗 颖,黄森焰,徐松林
基于频率安全约束与临界惯量计算的分时段限制风电出力方法
李世春,田冰杰,李惠子,罗 颖,黄森焰,徐松林
(三峡大学电气与新能源学院,湖北 宜昌 443002)
高比例风电接入导致系统等效惯量降低,增加了电网引发频率失稳的可能性。为保障日内频率安全稳定运行,同时避免大面积切除风电的不合理操作,提出了基于频率安全约束与临界惯量计算的分时段限制风电出力方法。通过引入频率最低点和最大频率变化率约束指标,并考虑日内运行方式变化,分时段求解电网临界惯量及对应的最大风电并网容量。结合电网实际惯量判定小于临界惯量的时段,对这些时段依据最大风电并网容量确定风电切除量,从而在日内各时段消除频率安全隐患。最后通过算例系统证明:所提方法能准确筛查电网日内存在频率安全风险的时段,求解的风功率分时段切除量可有效消除频率安全隐患。
高比例风电;频率安全约束;临界惯量;最大风电并网容量;风电切除量
0 引言
在国家碳达峰、碳中和的目标引领下,风电大规模、高比例接入电网[1-3],将会导致电力系统等效惯量持续降低、频率稳定运行能力显著削弱[4-6]。目前,在应对大规模风电并网引起的潜在电网安全稳定问题时,主要采取限制风电出力的方法[7-9],通过对风电场直接解列的“一刀切”方式来实施,往往会造成大量弃风,牺牲不必要的发电效益。鉴于此,当面临频率安全威胁时,制定合理的风电切除方案、通过准确计算频率安全约束下的风电最大并网容量来确定切除量,对于科学指导风电并网、保障电网频率安全具有重要意义。
关于风电最大并网容量的计算问题,一些学者从不同角度开展过相关研究。文献[10-11]考虑风速的随机性,应用机会约束规划理论,在满足系统潮流约束下,将风电接入容量最大化作为优化目标来求解风电穿透功率极限。文献[12]在考虑风电时空分布特征和功率平衡条件下,通过引入切负荷量和弃风量等风险指标,建立受限风险阈值下的多变量、非线性优化模型,求解了风电准入容量。上述研究从规划或稳态优化运行角度研究风电最大并网容量,未涉及电网安全稳定约束因素。随着风电渗透率不断提高,电网频率安全稳定水平已经成为限制风电并网容量的主要因素之一。
近年来,也有学者基于频率稳定约束研究风电最大并网容量计算问题。文献[13]基于风电参与调频的前提条件,考虑稳态频率偏差和频率变化率约束求解风电穿透功率极限,但该研究方法不能适应电网运行方式变化下的计算和应用。文献[14]通过对澳大利亚电网设置不同的风电渗透率,进行多次动态仿真试验,选择满足频率变化率和频率最低点约束的场景,以此求得系统的风电穿透功率极限,但该文献缺乏理论计算过程。文献[15]在分析不同风电渗透率对电力系统的等效惯量和发电机单位调节功率影响的基础上,计算评估了考虑最大频率跌落值和稳态频率偏差稳定约束的风电并网接纳能力。文献[16]建立了包含常规电源和可再生能源的电网频率响应综合模型,通过设置不同风电渗透率,分析扰动后频率变化率和最大频率偏移量,直至满足频率安全约束条件,最终确定可再生能源可接纳容量。上述研究通过计及频率稳定约束来求解风电最大并网容量,其计算过程和结果是粗略的。实际上,在1天24 h的各时段,电网惯量具有时变特征,风电等可再生能源出力也具有波动性,因此日内各时段的频率安全裕度存在差异,需要按时段确定最大风电并网容量,以精细化指导电网日常安全稳定运行。
综上所述,现有文献从规划或稳态优化运行角度研究风电最大并网容量,一部分文献虽然也考虑频率稳定约束求解风电最大并网容量,但存在理论计算过程缺乏和计算太粗略的问题,无法科学细致地指导电网日常频率安全稳定运行的具体操作。鉴于此,本文提出基于频率安全约束与临界惯量计算的分时段限制风电出力方法,以下详细论述其理论计算过程。
1 基于频率安全约束的风电最大并网容量计算
1.1 频率安全约束指标


1.2 计算风电最大并网容量的基本原理
若将电力系统等效为一个整体,其等值转子运动方程[17]可表示为

根据式(2)可求得最大频率偏差和频率变化率。
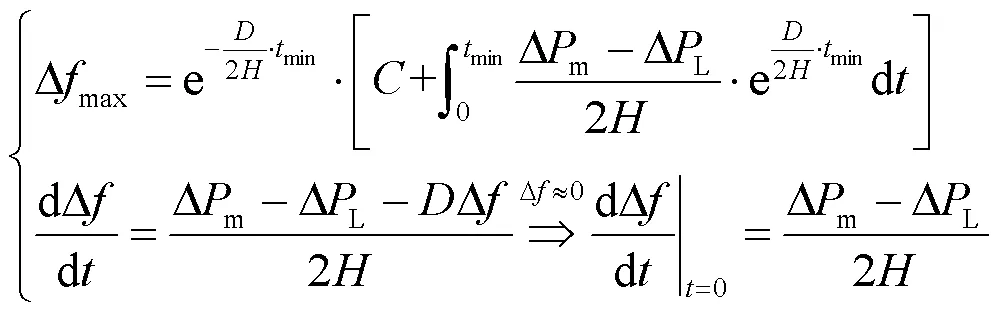

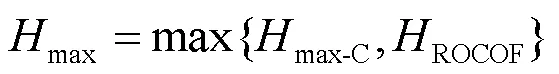
若电网包含台同步机组和个风电场,日内时段的等效惯量[13]为
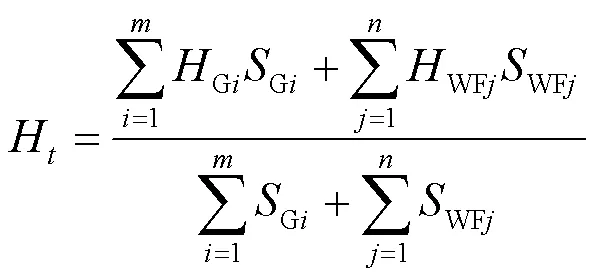

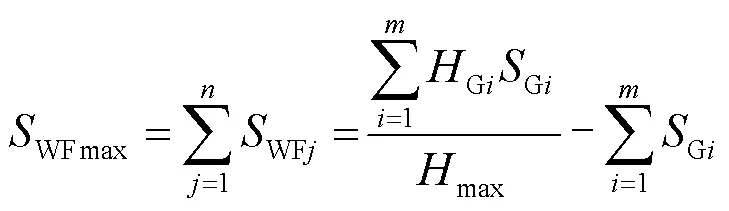
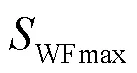
2 临界惯量和电网实际惯量计算
在式(7)中,若要求解WFmax,须先计算得到电网临界惯量和低于临界惯量的时段。因此,电网分时段实际惯量和临界惯量计算是本文研究的核心问题,以下详细论述其过程。
2.1 电网惯量计算
由式(5)可知,计算次日电网分时段实际惯量,需知次日同步机组启停状况和风电并网容量。从调度中心获取次日发电计划,可获得机组组合及其对应的惯性时间常数。短期风电功率预测可以预测次日零时起3天内的风电输出功率[18],预测点时间分辨率为15 min。短期风电功率负荷预测技术在电网调度应用方面比较成熟,且可用超短期风电功率预测值、实时风电功率滚动修正风电功率出力曲线。本文默认已得到风电功率出力曲线。
2.2 基于频率安全指标求解临界惯量
2.2.1频率最低点约束的临界惯量
可采用平均系统频率(Average System Frequency, ASF)响应模型[19-21]来描述包含多台同步机组的电力系统频率响应特性,并可将各机组调速系统模型采用一阶惯性环节来近似反映其响应过程[22],如图1所示。

图1 多机系统的频率响应闭环传递函数模型
图1中同步机组一次调频响应的机械功率增量可表示为

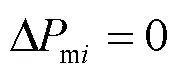
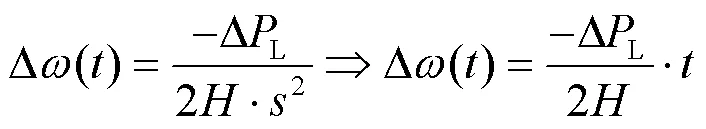
由式(9)可见,系统频率偏差由初始功率缺额和系统惯量决定,并与时间t呈线性比例关系,在该时间段内、易于求解。另一方面,频率跌落最低点通常在功率缺额扰动后3~5 s到达,此刻一次调频响应即开始动作。因此,可将频率跌落最低点到达之前、经式(9)计算的频率偏差作为计算频率跌落最低点时刻的同步机组一次调频机械功率增量的输入,这实际上是将图1的闭环传递函数模型打开为如图2所示开环模型,可简化求解。
根据图2所示的传递函数模型,将式(9)的时域表达式代入式(8),并进行拉式反变换后可得

在研究电网频率降到最低点的过程中,可对同步机组的机械功率增量进行线性化处理,用常系数一次函数近似表达其机械功率增量。对于典型系统,C可取频率最低点时刻对应的值[22]。
设系统频率最低点时刻为min,则同步机组对应的机械功率增量为
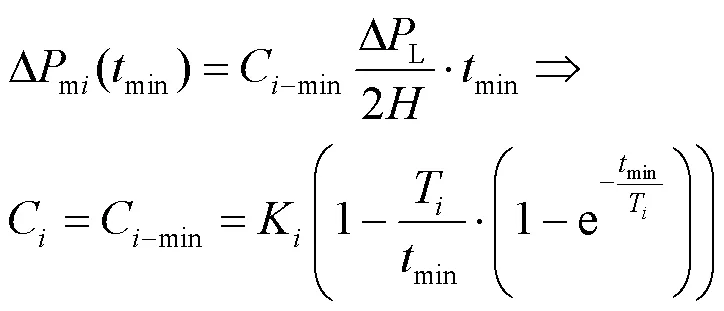
根据上述分析并结合图2可知,受扰后整个系统的动态频率方程为
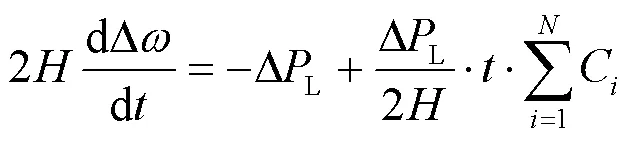
式中,表示同步机组的台数。
对式(12)两端积分并整理后可得
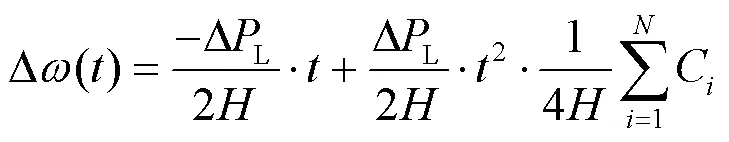
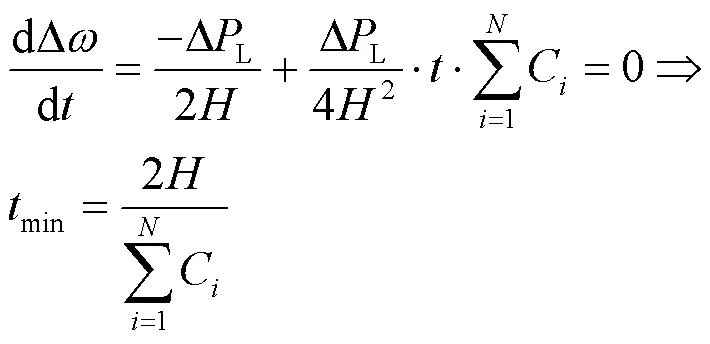
将式(14)代入式(13),计算频率最低点对应的最大角频率偏差为
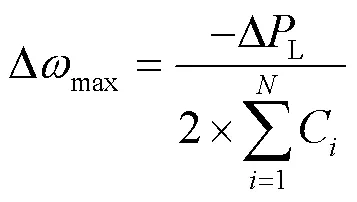
再转换为最大系统频率偏差的有名值,如式(16)所示。


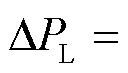
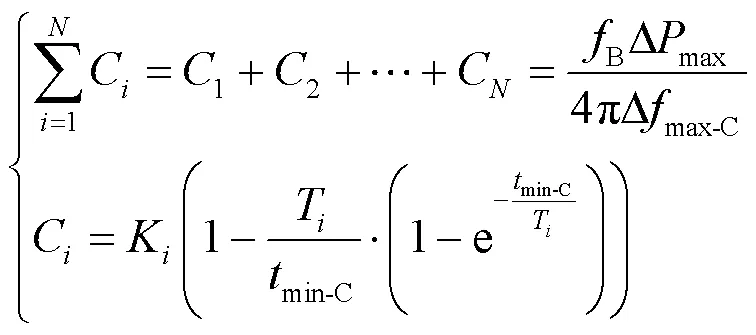
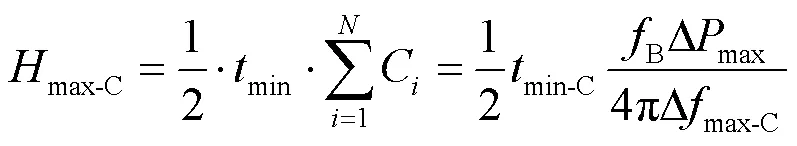
2.2.2频率变化率约束的临界惯量
系统最大频率变化率出现在扰动发生后瞬间,同步机组机械功率增量和等值阻尼系数都可忽略,根据式(3),最大频率变化率[23]可等效为
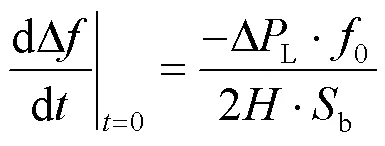
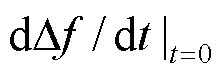

由前述分析可知,电网临界惯量应取式(18)和式(20)中较大值。

3 风电最大并网容量计算
将电力系统各时段电网实际惯量H与其对应临界惯量进行比较。如果H<max,表明此时段的电网惯量不满足临界惯量要求,需要切除部分风电出力,以消除频率安全隐患;如果H≥max,则电网惯量满足临界惯量要求,电网无频率安全隐患,基于文中前述理论分析过程,风电最大并网容量计算流程图如附图A1。
系统大功率缺额分为负荷突增和同步机组脱网两类,以下分别探讨两者对应的风电最大并网容量。
3.1 负荷突增下的风电最大并网容量计算
根据上述公式计算各时段的电网惯量H和电网临界惯量1max。对于电网惯量低于临界惯量时段,令切除风电后的电网惯量恰等于此时的临界惯量,根据式(7)可求得风电最大并网容量为
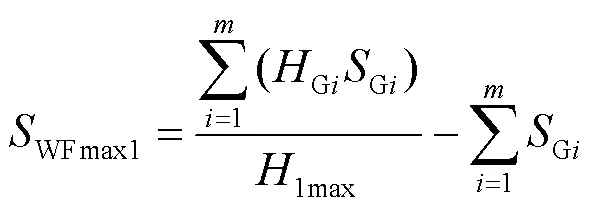
3.2 同步机组脱网下的风电最大并网容量计算
同步机组脱网会造成电网损失掉一部分惯量,从而呈现和负荷突增扰动不同的频率响应过程。因此,此类型故障下临界惯量应有所提高,保证电网在损失一部分惯量后仍满足动态频率安全约束。计算得到各时段的电网惯量H和同步机组脱网故障下的电网临界惯量2max。对于电网惯量低于临界惯量时段,令切除风电后的电网惯量恰等于临界惯量,根据式(7)可求得风电最大并网容量为

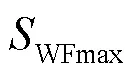

4 算例分析与验证
采用如图4所示IEEE-39算例系统,在Matlab/ Simulink下验证计算方法和结果的正确性、有效性。同步机组参数(发电机惯性时间常数、功频特性系数、调速器响应时间常数)如附表A1所示,同步机组各时段发电计划如附录表A2所示。
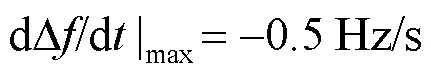
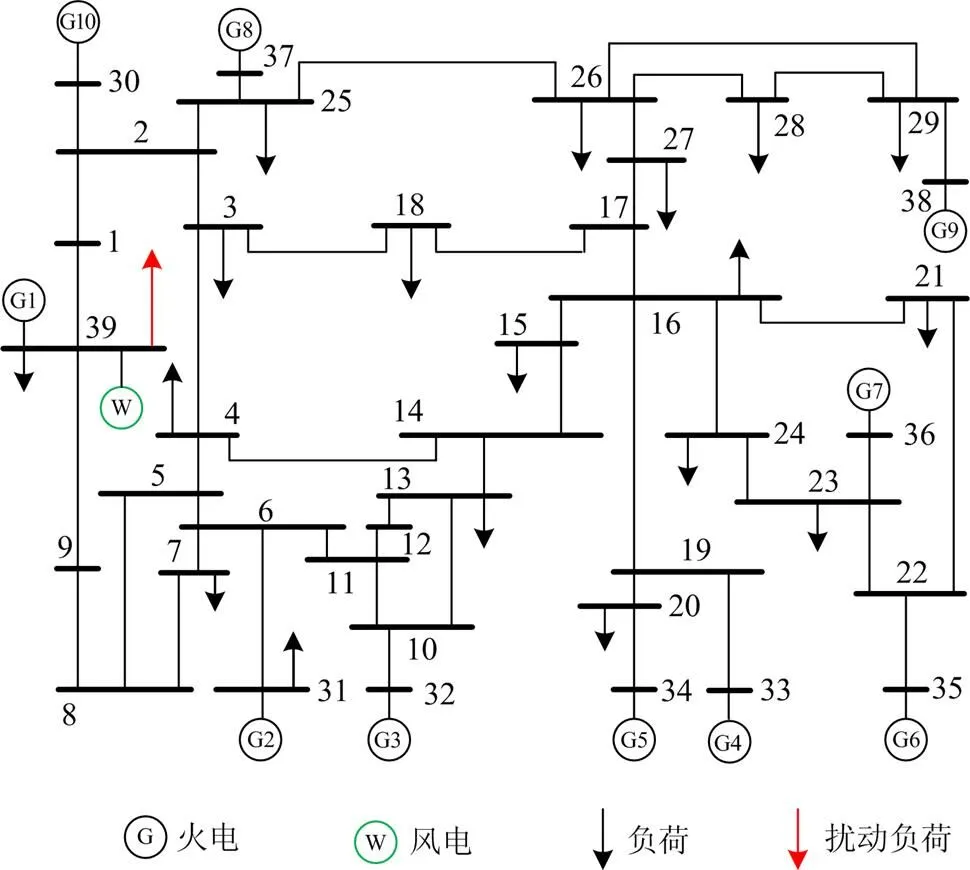
图4 算例系统

图5 各时段风电功率值
以下分别针对负荷突增和同步机组脱网两种典型功率缺额状况,求解对应的临界电网惯量和风电最大并网容量,并进行仿真计算与分析。
4.1 负荷突增时的计算分析
考虑较严重的实际情况,设置突增负荷占总负荷的15%。根据附表A2的同步机组各时段发电计划和风电功率预测结果,利用式(5)计算得到算例系统1天24 h的电网惯量,并通过式(21)求解电网临界惯量,如图6所示。

图6 负荷突增时的电网惯量与临界惯量
由图6可知,电网惯量和临界惯量均具有时变特征,使得一天中某些时段电网惯量小于临界惯量,如01:00—02:00、18:00—22:00时段。因此,需对这些时段限制风电功率,以消除频率安全隐患。
可利用式(22)求得上述时段对应的风电最大并网容量及其切除量,具体结果如附图A2和附表A3所示。在不同时段需切除对应的风电功率,例如在19:00—21:00时段需切除较大风电功率,来满足电网临界惯量要求。
为验证上述风电最大并网容量及其切除量的正确性和准确性,分别在01:00—01:15和19:00—19:15时段150 s处设置突增15%额定负荷,两个时段风速分别为12 m/s和10 m/s。对比仿真切除/不切除风电的系统频率受扰曲线,具体如图7—图10所示。
在01:00—01:15时段发生负荷突增功率缺额时,由图7、图8可知:1) 当不对风电出力限制时(不切除),频率跌落最低点达到48.86 Hz,低于最低频率跌落安全值49 Hz。通过限制风电出力,切除408 MW风电功率,可使频率跌落最低点恰好满足49 Hz的频率安全值要求;2) 无论是否限制风电功率,系统频率变化率均可满足-0.5 Hz/s安全值要求,这说明在该状况下,通过式(21)计算临界惯量和利用式(22)计算最大风电并网容量时,系统频率跌落最低点约束指标是主导因素。
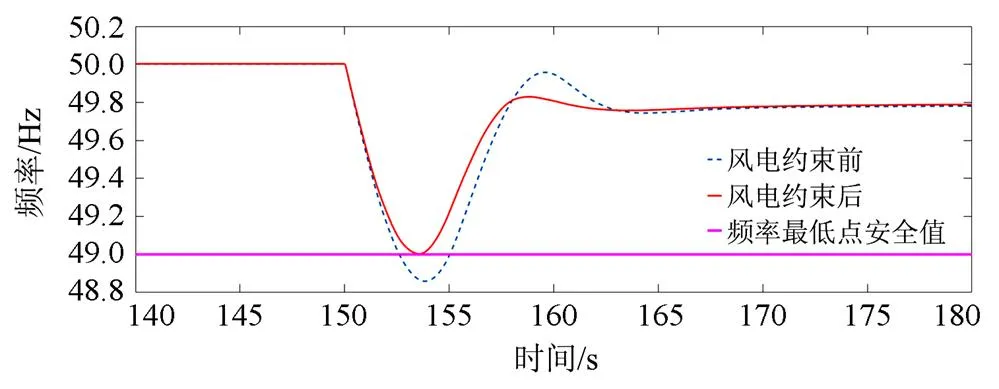
图7 01:00—01:15时段负荷突增的频率受扰曲线

图8 01:00—01:15时段负荷突增的频率变化率曲线

图9 19:00—19:15时段负荷突增的频率受扰曲线
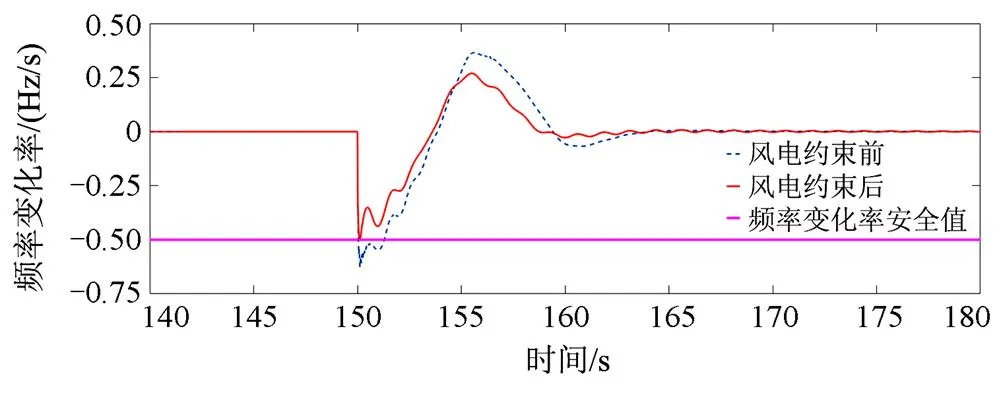
图10 19:00—19:15时段负荷突增的频率变化率曲线
在19:00—19:15时段发生负荷突增功率缺额时,由图9、图10可知:1) 当不对风电出力限制时(不切除),频率变化率最大值达到-0.625 Hz/s,超过了频率变化率安全值-0.5 Hz/s。通过限制风电功率,切除489 MW风电功率,可使频率变化率最大值满足-0.5 Hz/s安全值要求。2) 另一方面,当不限制风电功率时,系统频率跌落最低点低于最低频率跌落安全值49 Hz。当限制功率时(切除489 MW),系统频率最低点显著高于49 Hz。这说明在该状况下,通过式(21)计算临界惯量和利用式(22)计算最大风电并网容量时,系统频率变化率约束指标是主导因素,为了保证该约束指标,切除了489 MW风电功率,而实际上该切除量足以保证系统频率跌落最低点安全约束。
上述仿真计算与分析表明,在突增负荷时,本文对于风电最大并网容量及其切除量的计算结果能非常准确地控制在最大频率跌落最低点约束指标值或最大频率变化率约束指标值范围内,证明了本文计算方法的正确性和计算结果的准确性。
4.2 同步机组脱网时的计算分析
在此设置算例系统中机组G9脱网,由于同步机组脱网会影响到系统惯量,因此电网惯量和临界惯量计算结果与负荷突增的情况存在一定差异。此时,同样根据附表A2的同步机组各时段发电计划和风电功率预测结果,利用式(5)计算得到算例系统1天24 h的电网惯量,并通过式(21)求解临界惯量,如图11所示。
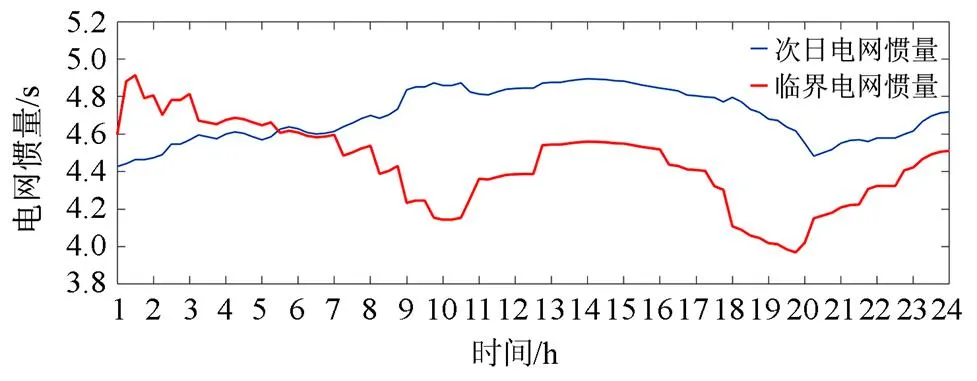
图11 同步机组脱网时的电网惯量与临界惯量
由图11可知,电网惯量小于临界惯量的时段主要在01:00—05:00。同样地,需对这些时段限制风电功率,以消除频率安全隐患。
可利用式(23)求得上述时段对应的风电最大并网容量及其切除量,具体结果如附图A3和附表A4所示。在01:00—05:00时段切除一定量的风电功率,即可满足临界惯量的要求。
为验证上述风电最大并网容量及其切除量的正确性和准确性,考虑算例系统中较大容量机组脱网情况,分别在01:00—01:15和02:00—02:15时段150 s处设置G9脱网,两个时段风速分别为12 m/s和10.8 m/s。对比仿真切除/不切除风电的系统频率受扰曲线,具体如图12—图15所示。

图12 01:00—01:15时段机组脱网的频率受扰曲线
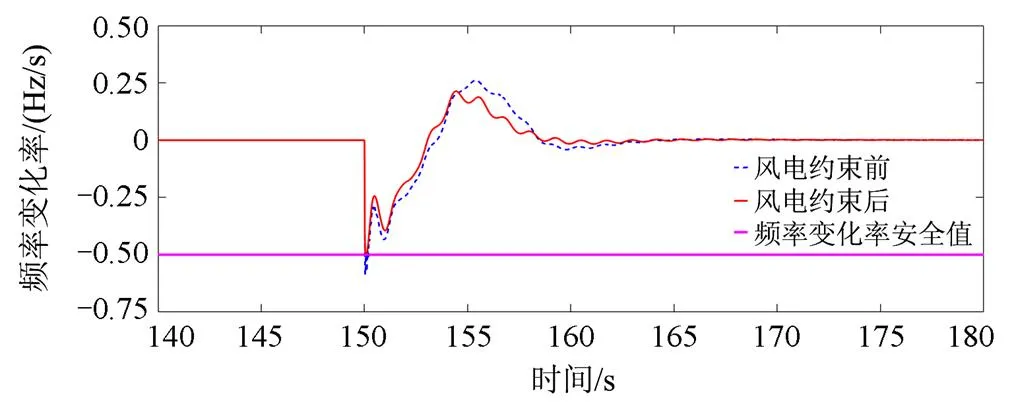
图13 01:00—01:15时段机组脱网的频率变化率曲线
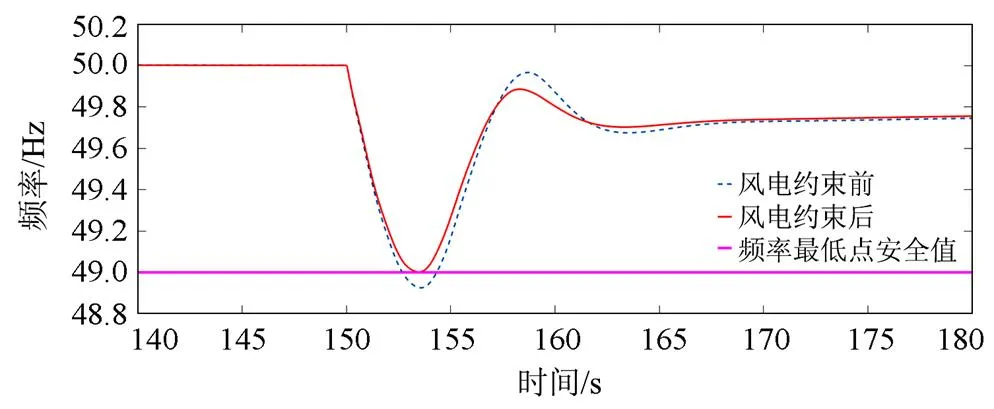
图14 02:00—02:15时段机组脱网的频率受扰曲线

图15 02:00—02:15时段机组脱网的频率变化率曲线
在01:00—01:15时段发生机组G9脱网时,由图12、图13可知:1) 当不对风电出力限制时(不切除),频率变化率最大值达到-0.58 Hz/s,超过了频率变化率安全值-0.5 Hz/s。通过限制风电出力,切除363 MW风电功率,可使频率变化率最大值满足-0.5 Hz/s安全值要求。2) 另一方面,当不限制风电功率时,系统频率跌落最低点超过最低频率跌落安全值49 Hz。当限制出力时(切除363 MW),系统频率最低点显著高于49 Hz。这说明在该状况下,通过式(21)计算临界惯量和利用式(23)计算最大风电并网容量时,系统频率变化率约束指标是主导因素,为了保证该约束指标,切除了363 MW风电功率,而实际上该切除量足以保证系统频率跌落最低点安全约束。
在02:00—02:15时段发生机组G9脱网时,由图14、图15可知:1) 当不对风电功率限制时(不切除),频率跌落最低点达到48.93 Hz,低于最低频率跌落安全值49 Hz。通过限制风电出力,切除335 MW风电功率,可使频率跌落最低点恰好满足49 Hz安全值要求。2) 无论是否限制风电功率,系统频率变化率均可满足-0.5 Hz/s的安全值要求,这说明在该状况下,通过式(21)计算临界惯量和利用式(23)计算最大风电并网容量时,系统频率跌落最低点约束指标是主导因素。
上述仿真计算与分析表明,在同步机组脱网时,本文对于风电最大并网容量及其切除量的计算结果能准确地控制在最大频率跌落最低点约束指标值或最大频率变化率约束指标值范围内,证明了本文计算方法的正确性和计算结果的准确性。
综上可知,在负荷突增和机组脱网两种典型功率缺额状况下,切除一定量的风电后,可保障频率变化率和频率最低点均在安全值内,证明了本文所提风电最大并网容量及其切除量计算方法的正确性和计算结果的准确性。
4.3 风电功率预测误差对本文风电切除方案影响分析
对风电出力实际值和经超短期风电功率滚动修正后平均绝对误差为5%的预测值[26-29]进行对比,如图16所示。
分别对风电功率实际值和预测值对应的风电切除量进行计算,可得图17。
由图17可知,图中风电切除量最小误差仅为0.8%,最大误差为9.2%,其主要原因在于风电功率预测误差为11.1%。次日风电切除量平均绝对误差仅为3.8%,整体误差较小。由此可得超短期风电功率预测滚动修正下的风电切除方案精确度较高。在工程实际操作运行时,可通过超短期风电功率预测、实时风电功率对次日风电功率预测值进行滚动修正求解,从而提高风电功率切除的精确性。
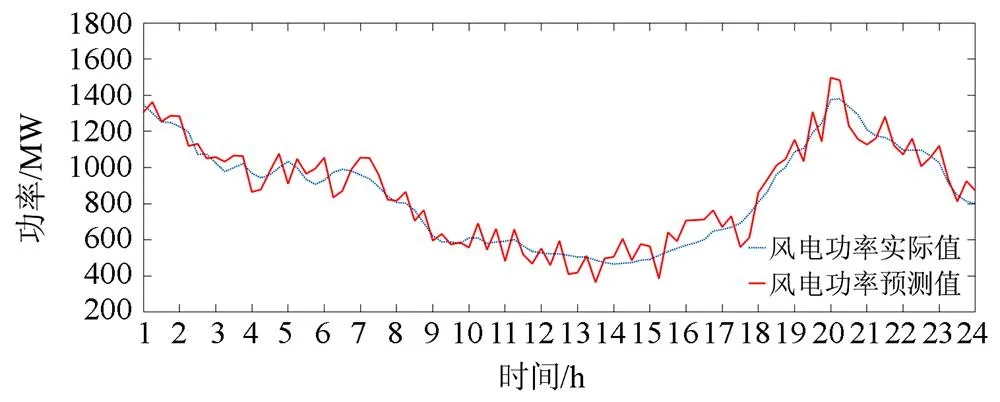
图16 风电功率预测值和实际值的对比
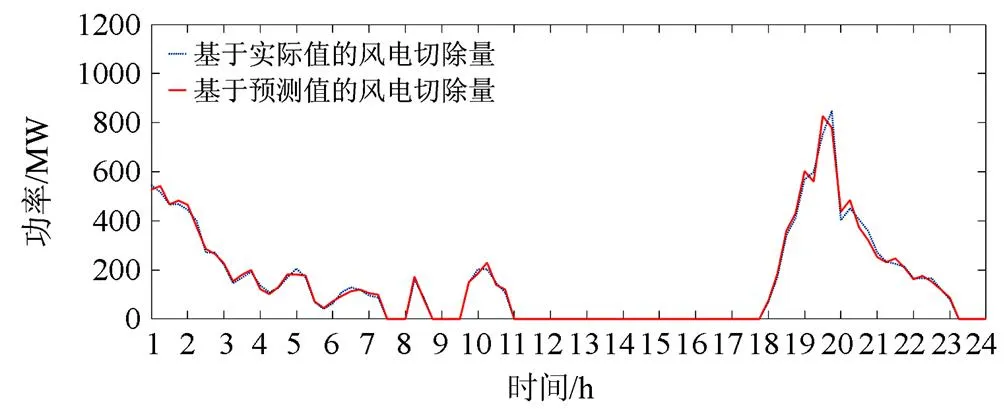
图17 风电功率预测值和实际值对应的风电切除量
4.4 风电最大并网容量及切除量的确定
上述部分验证了两种功率缺额场景下风电最大并网容量及其切除量计算方法的正确性和计算结果的准确性,并针对风电功率预测误差下的风电切除方案进行相应修正处理。在实际取值时还须根据式(24)取两种场景下、各时段的风电并网容量较小值和切除量较大值,据此得出如图18所示结果。
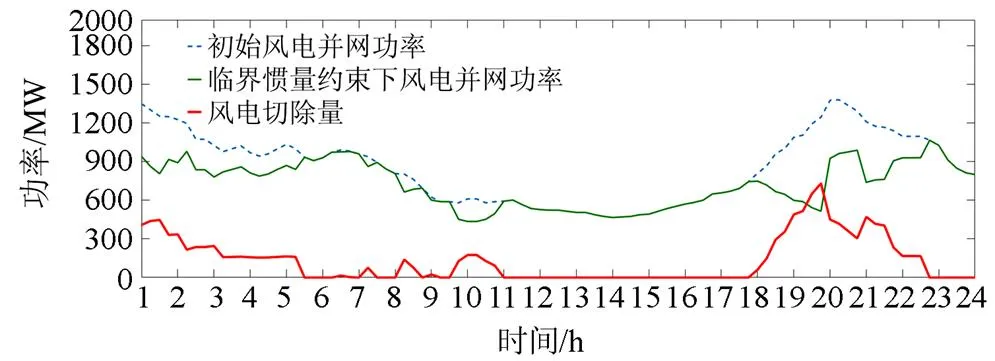
图18 一天中风电最大并网容量及切除量
5 结论
本文应用频率安全约束和临界惯量,对风电场最大并网容量及其切除量进行计算,得出如下结论:
1) 根据频率跌落最低点和最大频率变化率约束指标分时段求得的临界惯量,可快速准确地判断电网存在频率安全隐患的时段。
2) 电网惯量和临界惯量均具有时变特征,对于电网实际惯量小于临界惯量时段,应用本文计算方法可对风电场并网容量进行定量切除,从而保证电网故障下的频率安全。
3) 随着风电虚拟惯性控制和储能技术的进一步发展,未来风电场将会具备一定的惯性响应能力。在动态频率安全约束下的风电并网能力将会发生改变,这将是下一步研究的内容。
附表A1 发电机组参数
Attached Table A1 Generator set parameters
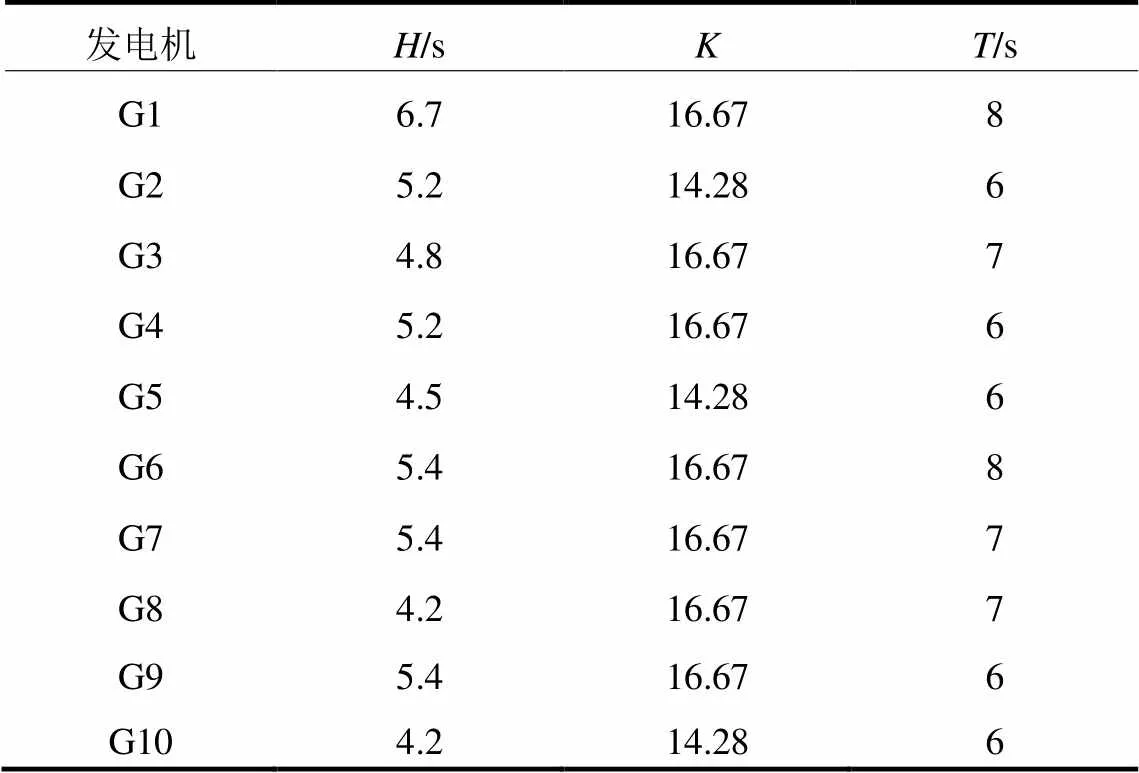
发电机H/sKT/s G16.716.678 G25.214.286 G34.816.677 G45.216.676 G54.514.286 G65.416.678 G75.416.677 G84.216.677 G95.416.676 G104.214.286
附图A1 次日分时段风电最大并网功率计算流程图
Attached Fig. A1 Calculation flow chart of the maximum grid-connected capacity of wind power in different periods of the next day
附表A2 各时段发电计划
Attached Table A2 Power generation plan for each time period
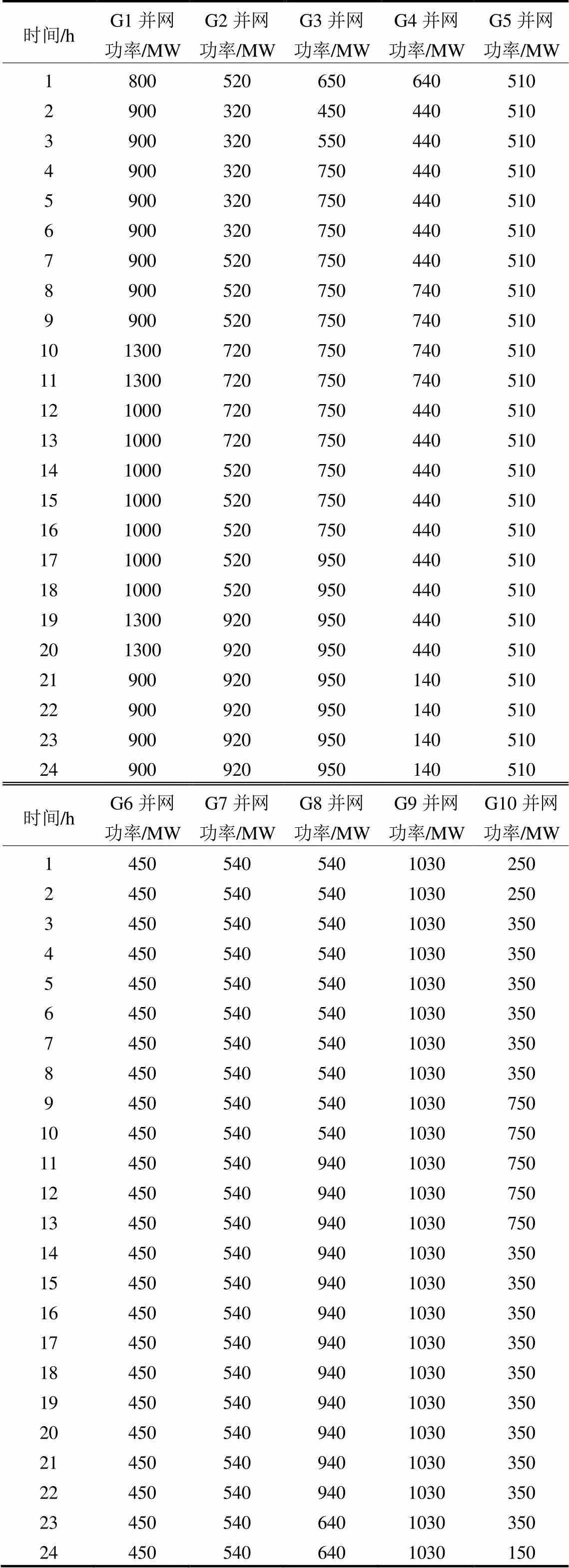
时间/hG1并网功率/MWG2并网功率/MWG3并网功率/MWG4并网功率/MWG5并网功率/MW 1800520650640510 2900320450440510 3900320550440510 4900320750440510 5900320750440510 6900320750440510 7900520750440510 8900520750740510 9900520750740510 101300720750740510 111300720750740510 121000720750440510 131000720750440510 141000520750440510 151000520750440510 161000520750440510 171000520950440510 181000520950440510 191300920950440510 201300920950440510 21900920950140510 22900920950140510 23900920950140510 24900920950140510 时间/hG6并网功率/MWG7并网功率/MWG8并网功率/MWG9并网功率/MWG10并网功率/MW 14505405401030250 24505405401030250 34505405401030350 44505405401030350 54505405401030350 64505405401030350 74505405401030350 84505405401030350 94505405401030750 104505405401030750 114505409401030750 124505409401030750 134505409401030750 144505409401030350 154505409401030350 164505409401030350 174505409401030350 184505409401030350 194505409401030350 204505409401030350 214505409401030350 224505409401030350 234505406401030350 244505406401030150
附图A2 负荷突增下的风电最大并网功率和风电切除量
Attached Fig. A2 Maximum grid-connected capacity and removal of wind power under sudden load increase
附A3 负荷突增下的风电最大并网功率和风电切除量
Attached Table A3 Maximum grid-connected capacity and removal of wind power under sudden load increase
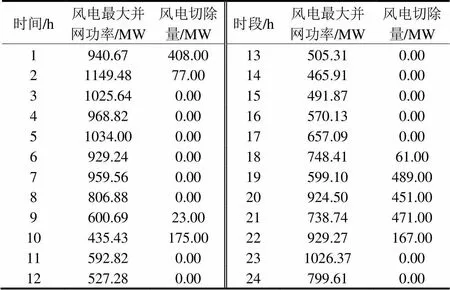
时间/h风电最大并网功率/MW风电切除量/MW时段/h风电最大并网功率/MW风电切除量/MW 1940.67408.0013505.310.00 21149.4877.0014465.910.00 31025.640.0015491.870.00 4968.820.0016570.130.00 51034.000.0017657.090.00 6929.240.0018748.4161.00 7959.560.0019599.10489.00 8806.880.0020924.50451.00 9600.6923.0021738.74471.00 10435.43175.0022929.27167.00 11592.820.00231026.370.00 12527.280.0024799.610.00
附图A3 同步机组脱网下风电最大并网功率和风电切除量
Attached Fig. A3 Maximum grid-connected capacity and cut-off amount of wind power when synchronized generators are off-grid
附表A4 同步机组脱网下风电最大并网功率和风电切除量
Attached Table A4 Maximum grid-connected capacity and cut-off amount of wind power when synchronized generators are off-grid

时间/h风电最大并网功率/MW风电切除量/MW时段/h风电最大并网功率/MW风电切除量/MW 1985.67363.0013505.310.00 2891.48335.0014465.910.00 3780.64245.0015491.870.00 4811.82157.0016570.130.00 5870.00164.0017657.090.00 6929.240.0018809.410.00 7959.560.00191088.100.00 8806.880.00201375.500.00 9623.690.00211209.740.00 10610.430.00221096.270.00 11592.820.00231026.370.00 12527.280.0024799.610.00
[1] 赵福林, 俞啸玲, 杜诗嘉, 等. 计及需求响应的含大规模风电并网下电力系统灵活性评估[J]. 电力系统保护与控制, 2021, 49(1): 42-51.
ZHAO Fulin, YU Xiaoling, DU Shijia, et al. Assessment on flexibility of a power grid with large-scale wind farm integration considering demand response[J]. Power System Protection and Control, 2021, 49(1): 42-51.
[2] 李德鑫, 宗崇林, 黄大为, 等. 大规模风电汇聚外送的区域送端电力系统两级优化调度[J]. 电力系统保护与控制, 2021, 49(11): 35-44.
LI Dexin, ZONG Chonglin, HUANG Dawei, et al. Two-level optimal dispatching of regional transmission end power system for large-scale wind power convergence and external transmission[J]. Power System Protection and Control, 2021, 49(11): 35-44.
[3] 孙伟卿, 罗静, 张婕. 高比例风电接入的电力系统储能容量配置及影响因素分析[J]. 电力系统保护与控制, 2021, 49(15): 9-18.
SUN Weiqing, LUO Jing, ZHANG Jie. Energy storage capacity allocation and influence factor analysis of a power system with a high proportion of wind power[J]. Power System Protection and Control, 2021, 49(15): 9-18.
[4] 孙华东, 许涛, 郭强, 等. 英国“8•9”大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192.
SUN Huadong, XU Tao, GUO Qiang, et al. Analysis on blackout in Great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192.
[5] ERDIWANSYAH, MAHIDIN, HUSIN H, et al. A critical review of the integration of renewable energy sources with various technologies[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 37-54.
[6] 刘英琪, 谢敏, 韦薇, 等. 高比例风电接入的电力系统灵活性评估与优化[J]. 电力建设, 2019, 40(9): 1-10.
LIU Yingqi, XIE Min, WEI Wei, et al. Assessment and optimization for power system flexibility with high proportion of wind power[J]. Electric Power Construction, 2019, 40(9): 1-10.
[7] 陈赟, 陈得治, 马世英, 等. 风光火打捆交直流外送系统的高频切机方案研究[J]. 电网技术, 2016, 40(1): 186-192.
CHEN Yun, CHEN Dezhi, MA Shiying, et al. Studies on high-frequency generator tripping strategy for wind-photovoltaic-thermal-bundled power transmitted by AC/DC system[J]. Power System Technology, 2016, 40(1): 186-192.
[8] 丁剑, 邱跃丰, 孙华东, 等. 大规模风电接入下风电机组切机措施研究[J]. 中国电机工程学报, 2011, 31(19): 25-36.
DING Jian, QIU Yuefeng, SUN Huadong, et al. Consideration of wind generator tripping under large-scale wind power integration[J]. Proceedings of the CSEE, 2011, 31(19): 25-36.
[9] 岳涵, 邵广惠, 孙铭泽, 等. 含大规模新能源集中外送型电网高频第三道防线配置方法[J]. 电网技术, 2019, 43(5): 1766-1771.
YUE Han, SHAO Guanghui, SUN Mingze, et al. A configuration method of high frequency third defensive line for power-integrated-exporting grid with large-scale renewable energy[J]. Power System Technology, 2019, 43(5): 1766-1771.
[10]王锐, 顾伟, 孙蓉, 等. 基于概率最优潮流的风电接入能力分析[J]. 电网技术, 2011, 35(12): 214-220.
WANG Rui, GU Wei, SUN Rong, et al. Analysis on wind power penetration limit based on probabilistically optimal power flow[J]. Power System Technology, 2011, 35(12): 214-220.
[11]汤雪松, 殷明慧, 邹云. 考虑风速相关性的风电穿透功率极限的改进计算[J]. 电网技术, 2015, 39(2): 420-425.
TANG Xuesong, YIN Minghui, ZOU Yun. An improved method to calculate wind power penetration limit considering wind speed correlation[J]. Power System Technology, 2015, 39(2): 420-425.
[12]曲正伟, 王京波, 王云静, 等. 考虑运行风险约束的风电场群准入容量分析[J]. 电网技术, 2014, 38(7): 1861-1866.
QU Zhengwei, WANG Jingbo, WANG Yunjing, et al. Analysis on acceptable capacity of wind farm group considering operation risk constraints[J]. Power System Technology, 2014, 38(7): 1861-1866.
[13] 李世春, 唐红艳, 邓长虹, 等. 考虑频率约束及风电机组调频的风电穿透功率极限计算[J]. 电力系统自动化, 2019, 43(4): 33-43.
LI Shichun, TANG Hongyan, DENG Changhong, et al. Calculation of wind power penetration limit involving frequency constraints and frequency regulation of wind turbines[J]. Automation of Electric Power Systems, 2019, 43(4): 33-43.
[14] AHMADYAR A, RIAZ S, VERBIC G, et al. A framework for assessing renewable integration limits with respect to frequency performance[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4444-4453.
[15] 谢岩, 马世英, 唐晓骏. 频率稳定约束条件下风电并网能力的确定方法[J]. 电力系统及其自动化学报, 2021, 33(8): 130-137.
XIE Yan, MA Shiying, TANG Xiaojun. Determination of wind power grid connection capability under frequency stability constraints[J]. Proceedings of the CSU-EPSA, 2021, 33(8): 130-137.
[16] 郭小龙, 毕天姝, 刘方蕾, 等. 风、光高渗透率电网中考虑频率稳定的可再生能源承载力研究[J]. 可再生能源, 2020, 38(1): 84-90.
GUO Xiaolong, BI Tianshu, LIU Fanglei, et al. Estimating maximum penetration level of renewable energy based on frequency stability constrains in networks with high penetration wind and photovoltaic energy[J]. Renewable Energy, 2020, 38(1): 84-90.
[17] 李世春, 夏智雄, 程绪长, 等. 基于类噪声扰动的电网惯量常态化连续估计方法[J]. 中国电机工程学报, 2020, 40(14): 4430-4439, 4723.
LI Shichun, XIA Zhixiong, CHENG Xuchang, et al. Continuous estimation method of power system inertia based on ambient disturbance[J]. Proceedings of the CSEE, 2020, 40(14): 4430-4439, 4723.
[18] LI Zhi, YE Lin, ZHAO Yongning, et al. Short-term wind power prediction based on extreme learning machine with error correction[J]. Protection and Control of Modern Power Systems, 2016, 1(1): 9-16.
[19] HUANG H, JU P, JIN Y, et al. Generic system frequency response model for power grids with different generations[J]. IEEE Access, 2020, 8: 14314-14321.
[20] JU Ping, ZHENG Yi, JIN Yuqing, et al. Analytic assessment of the power system frequency security[J]. IET Generation, Transmission & Distribution, 2021, 15(15): 2215-2225.
[21] 吴雪莲, 李兆伟, 刘福锁, 等. 大功率扰动下计及系统频率分布特性的紧急控制策略研究[J]. 电力系统保护与控制, 2021, 49(3): 104-114.
WU Xuelian, LI Zhaowei, LIU Fusuo, et al. Analysis of the emergency control strategy of system frequency considering system frequency distribution characteristics under large power disturbance[J]. Power System Protection and Control, 2021, 49(3): 104-114.
[22] EGIDO I, FERNANDEZ-BERNAL F, CENTENO P, et al. Maximum frequency deviation calculation in small isolated power systems[J]. IEEE Transactions on Power Systems, 2009, 24(4): 1731-1738.
[23] 王霞, 应黎明, 卢少平. 考虑动态频率约束的一次调频和二次调频联合优化模型[J]. 电网技术, 2020, 44(8): 2858-2867.
WANG Xia, YING Liming, LU Shaoping. Joint optimization model for primary and secondary frequency regulation considering dynamic frequency constraint[J]. Power System Technology, 2020, 44(8): 2858-2867.
[24]叶婧, 林涛, 张磊, 等. 考虑动态频率约束的含高渗透率光伏电源的孤立电网机组组合[J]. 电工技术学报, 2017, 32(13): 194-202.
YE Jing, LIN Tao, ZHANG Lei, et al. Isolated grid unit commitment with dynamic frequency constraint considering photovoltaic power plants participating in frequency regulation[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 194-202.
[25] 樊艳芳, 钟显, 常喜强, 等. 频率的时空分布对低频减载的影响研究[J]. 电力系统保护与控制, 2015, 43(1): 55-60.
FAN Yanfang, ZHONG Xian, CHANG Xiqiang, et al. Research of the UFLS under the frequency characteristics of temporal and spatial distribution[J]. Power System Protection and Control, 2015, 43(1): 55-60.
[26] 杨茂, 张罗宾. 基于数据驱动的超短期风电功率预测综述[J]. 电力系统保护与控制, 2019, 47(13): 171-186.
YANG Mao, ZHANG Luobin. Review on ultra-short term wind power forecasting based on data-driven approach[J]. Power System Protection and Control, 2019, 47(13): 171-186.
[27] 赵征, 汪向硕. 基于CEEMD和改进时间序列模型的超短期风功率多步预测[J]. 太阳能学报, 2020, 41(7): 352-358.
ZHAO Zheng, WANG Xiangshuo. Ultra-short-term multi-step wind power prediction based on CEEMD and improved time series model[J]. Acta Energiae Solaris Sinica, 2020, 41(7): 352-358.
[28] LIU J, SHI Q, HAN R, et al. A hybrid GA–PSO–CNN model for ultra-short-term wind power forecasting[J]. Energies, 2021, 14(20): 1-22.
[28] WU Q, GUAN F, LÜ C, et al. Ultra-short-term multi-step wind power forecasting based on CNN-LSTM[J]. IET Renewable Power Generation, 2021, 15(5): 1019-1029.
Method for limiting wind power output in time periods based on frequency safety constraints and a critical inertia calculation
LI Shichun, TIAN Bingjie, LI Huizi, LUO Ying, HUANG Senyan, XU Songlin
(College of Electrical Engineering and New Energy, China Three Gorges University, Yichang 443002, China)
The high proportion of wind power access to power systems leads to a reduction of the equivalent inertia of the system. This increases the possibility of frequency instability caused by the power grid. In order to ensure the safe and stable operation of the frequency during the day, and at the same time avoid the unreasonable step of removing wind power in a large area, a method of limiting wind power output based on frequency safety constraints and a critical inertia calculation is proposed. By introducing a frequency nadir and maximum rate of change of frequency constraint index, and considering the changes in the operation mode within the day, the critical inertia of the grid and the corresponding maximum wind power grid-connected capacity are calculated in time periods. A time period less than the critical inertia is determined based on the actual inertia of the grid, to determine the amount of wind power removal based on the maximum wind power grid-connected capacity. This is to eliminate hidden frequency safety hazards at various times of the day. Finally, a calculation example proves that the method proposed in this paper can accurately screen the time period of frequency safety risk in the grid day, and the calculated amount of wind power cut in time can effectively eliminate the hidden frequency safety hazard.
high proportion of wind power; frequency safety constraints; critical inertia; maximum wind power grid-connected capacity; wind power removal
10.19783/j.cnki.pspc.211322
2021-09-29;
2021-12-23
李世春(1984—),男,博士,副教授,研究方向为含新能源电力系统运行与控制;E-mail: lschunu_023@126.com
田冰杰(1997—),男,硕士研究生,研究方向为含新能源电力系统运行与控制。E-mail: 1354993460@qq.com
国家自然科学基金项目资助(51907104)
This work is supported by the National Natural Science Foundation of China (No. 51907104).
(编辑 周金梅)
