DE算法优化CNN的滚动轴承故障诊断研究

孙祺淳,李媛媛

（上海工程技术大学 电子电气工程学院，上海 201620）

滚动轴承是当今工业体系中最为关键的机械零件之一，同时也是非常容易出现故障的零件。滚动轴承若出现故障，不仅自身的运行状态会受到影响，与之相关联的各种零件与设备都会出现问题，轻则造成一定的生产损失，重则造成严重的安全事故。因此，提高轴承故障诊断的准确性和稳定性具有重要的理论和工程意义[1]。

在近些年，随着计算机性能的不断提升，机器学习和深度学习算法也广泛应用于滚动轴承的故障诊断中[2]。其中，卷积神经网络作为深度学习中最为经典的算法之一，已在计算机视觉和自然语言处理等领域中取得了优异的成果。近年来，也有越来越多的学者将卷积神经网络应用于机械设备的故障诊断中。

陈功胜等[3]利用CNN 来提取轴承数据的特征，再利用极限树回归实现故障诊断，结果表明此模型可以有效识别故障，并且具有较好的鲁棒性。赵敬娇等[4]提出一种基于残差连接的一维CNN 网络，基于残差连接的CNN可以更有效提取数据特征，从而提高故障诊断的精度。李益兵等[5]提出了一种基于混合蛙跳算法改进CNN的滚动轴承故障诊断方法，该方法利用混合蛙跳算法的寻优能力，自适应调整网络结构，提高了CNN 的特征提取能力，从而取得了良好的故障诊断效果。Wen 等[6]将用传感器采集的一维信号转换为二维的灰度图像，再将其输入至二维的基于LeNet-5的改进CNN网络中进行故障诊断，结果表明此模型在轴承、离心泵和液压泵3种数据集上都达到了较高的诊断精度。Viet 等[7]利用随机对角线算法训练CNN，使得CNN能够从数据中提取出更有效的特征，实验结果表明此模型对于滚动轴承的早期故障和复合故障都有很高的诊断精度。

上述学者的研究表明，基于CNN的滚动轴承故障诊断研究都利用了CNN强大的特征提取能力，将卷积层和池化层提取而来的特征经过全连接层或使用其他分类算法实现故障诊断。但是，在实际的工程应用中，确定出可靠有效的CNN模型超参数往往是非常困难的，若这些超参数设置不合理，则会极大影响CNN故障诊断的能力。

鉴于差分进化算法优异的寻优性能[8]，本文提出一种基于差分进化算法优化CNN 的滚动轴承故障诊断模型，通过差分进化算法来确定CNN的模型超参数，提高其精度和网络输出的稳定性。同时，为了更好提取滚动轴承运行数据的特征，本文使用CEEMDAN 分解原始信号，再结合峭度对分解得到的IMF 分量进行筛选，并使用多参数诊断的方法提取其特征。最后，本文使用CNN和CNN-DE等方法通过凯斯西储大学滚动轴承数据集进行对比，结果表明本文提出的算法模型拥有更高的精度和更稳定的性能，从而具有更可靠的工程应用价值。

1 卷积神经网络

1.1 卷积神经网络的基本结构

卷积神经网络是一种典型的前馈型神经网络，主要包括卷积层、池化层和全连接层。在分类任务中，在将原始数据输入到CNN 网络中后，由卷积层和池化层对其进行特征提取，再将提取出的特征输入到全连接层中，全连接层可以看作一个分类器，将输入的特征与标签建立起映射关系，从而实现分类。

可将卷积层视作一组卷积核在输入的数据矩阵中进行卷积运算。得到卷积输出之后，再通过一个激活函数对其进行非线性变化，从而得到一系列特征图，可表示为：

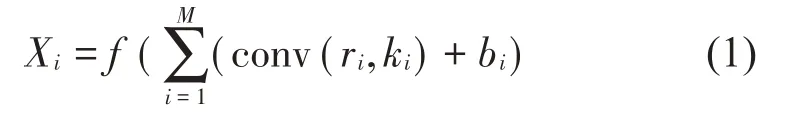
式(1)中：conv( )代表卷积函数，ri为输入卷积核的特征，ki为卷积核，bi为偏置，Xi代表每一层的特征图，M为特征图的总数，f( )为激活函数，本文选用ReLU作为激活函数。

池化层通常加在卷积层之后，用于降低数据的维数，在提高网络训练速度的同时降低过拟合的风险。常用的池化方法有最大值池化法和平均值池化法。顾名思义，这两种方法分别是从特征图中提取局部最大值与平均值，本文采用最大值池化方法：

式(2)中：max代表最大值池化函数，p代表降维之后的特征图。

由卷积层和池化层对原始数据进行交替作用之后，将最终得到的特征输入全连接层中。全连接层包含有隐藏层与输出层，其输出结果可视作一个概率分布，可表示为：

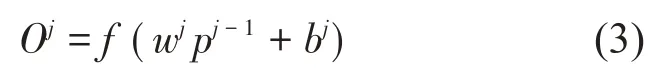
式(3)中：f( )代表激活函数，本文选用ReLU 作为隐含层的激活函数，wj代表第j层与第j+1 层之间的权值，pj-1代表第j-1层的输出，本文设置的全连接层层数为2。若j=1，p0则代表池化层的输出。bj代表第j层的偏置，Oj代表第j层的输出。通过softmax 函数来识别全连接层的输出概率，最终得到分类结果。

本文设置的CNN网络结构中包含两个卷积层、两个最大值池化层和全连接层；层与层之间的激活函数为ReLU，最后使用softmax输出故障诊断结果。

1.2 待优化的超参数选择

CNN 之类的神经网络模型所包含的参数通常可以分为模型参数与模型超参数。其中模型参数如偏置和权重等是网络通过不断的训练自动调整的，无需人工进行调节，故本文不做优化考虑；而对于模型超参数，网络无法通过训练自发对其进行调整，通常是在训练之前由人工设定，如学习率和训练的批量大小等等，但它们的取值通常依赖于经验，而经验值在解决具体问题时往往效果一般，从而导致基于CNN的滚动轴承故障诊断应用精度不高，网络输出不稳定。因此，本文针对CNN 的模型超参数（下文简称为超参数）进行优化，待优化的超参数及优化原因如下：

(1)训练的批量大小即为每一次训练时所选取的样本个数。若样本个数过多会导致计算机的内存占用过大；反之则容易导致CNN无法收敛。

(2)学习率即为梯度下降的大小。若学习率设置过大，容易出现梯度在最小值附近震荡的情况，从而导致CNN 无法收敛；反之则会导致CNN 收敛的速度极为缓慢。

(3)卷积核的大小。通常来说卷积核越大容易导致CNN 训练过程缓慢；反之则会影响CNN 提取特征的能力。

(4)卷积核的数量。通常来说卷积核的数量越多，越容易导致CNN 出现过拟合的情况；反之则容易导致CNN出现欠拟合的情况。

CNN的超参数不仅包括上文所提到的这些，根据不同的网络构建方式，超参数可能多达几十个甚至上百个。所以一般的做法是选择出最为关键的几个超参数进行调优。本文根据文献[5，9]和上述的分析，选择训练的批量大小、学习率、第一层卷积核的大小及数量、第二层卷积核的大小及数量共6 个值作为待优化的超参数。

2 基于CNN-DE的故障诊断模型

差分进化算法是由R.Storn 与K.Price 在1995年提出的一种基于种群的优化算法，在1996年举行的第一届国际进化优化方法竞赛(International Contest on Evolution Optimization，ICEO)中，DE 取得第三名的好成绩。相比其他的优化算法，DE的优势主要体现在它的可操控性上，只有3 个控制参数需要调节，结构简单，易于实现，同时拥有优秀的全局搜索能力[10]。

CNN-DE模型的流程如下：

(1)初始化种群

标准DE算法采用实数编码，首先生成一个规模为[N，D]的初始种群，N代表种群内个体数量，本文设置N=30；D代表决策变量的个数，在本文中D为待优化的CNN超参数个数，即D=6。初始种群可表示为：

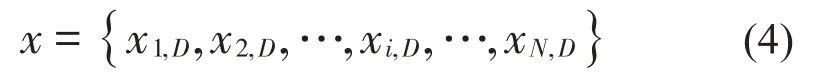
式(4)中：x代表初始种群，i∈[1，N]。种群内每一个个体向量维度都为6，每一个维度都分别代表一个CNN的超参数，即：

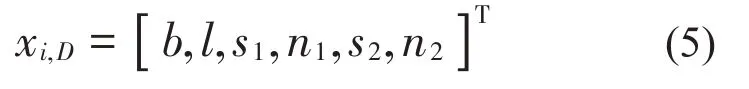
式中：b代表CNN的训练的批量大小，l代表CNN的学习率，s1代表CNN的第一层卷积核的大小，n1代表CNN的第一层卷积核的数量，s2代表CNN的第二层卷积核的大小，n2代表CNN 的第二层卷积核的数量。

(2)定义适应度函数

本文使用滚动轴承数据来训练CNN-DE 模型，并定义CNN-DE的适应度函数为：

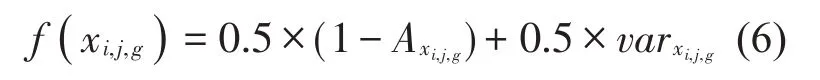
式中，记f(xi,j,g) 为第g代种群中第i个个体向量在第j个batch size 上的适应度函数值，g∈[1，G]，G代表DE算法迭代的总次数。

将xi,j,g中6 个超参数代入CNN 后，在第j个batch size上所得到的CNN精度记为Ax,i,j,g。将在前j个batch size 所得到的精度的方差记为varxi,j,g。精度越高，1-Axi,j,g的值就越小；CNN 输出结果越稳定，在各个batch size所得到的精度值的偏离程度就越低，即方差越小；将精度与方差分别乘以0.5的权重系数再相加得到适应度函数值。最终将优化问题转化为确定上述CNN 中6 个超参数的取值，从而使得适应度函数值最小的问题。

(3)变异

自DE算法提出以来，众多学者对其加以改进优化，也提出了许多新的变异算子。本文所使用的变异算子为：

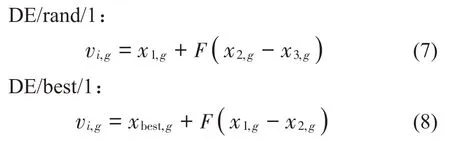
式(7)和式(8)中F为缩放因子，g为当前进化代数，x1,g、x2,g和x3,g为互不相同的个体向量。xbest,g为当前代中适应度函数值最小的个体向量，vi,g为变异向量。

DE/rand/1 算子可在DE 算法迭代的前期设置，用于增加种群的多样性，而DE/best/1 算子可在DE算法迭代的后期设置，用于加速算法的收敛[11]。因此，本文提出一种混合变异策略：

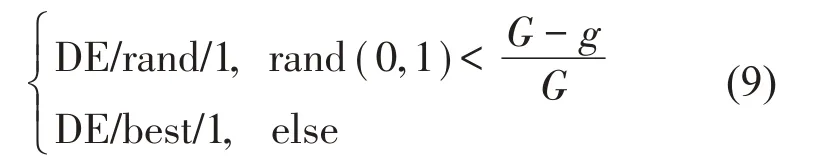
式中：rand(0,1)代表随机生成的0 至1 之间的随机数。在迭代的早期，(G-g)/G的值较小，不等式成立的概率比较大，因此，在DE 算法迭代的前期更容易选中DE/rand/1算子；反之，在迭代的后期，选中DE/best/1算子的概率更大，符合上文的要求。

对于缩放因子F，通常将其设定为一个定值，但如此一来容易导致DE算法陷入局部最优，降低其性能。考虑到在JADE(Adaptive Differential Evolution with Optional External Archive)算法中，采用高斯分布随机生成每一代的缩放因子效果较好，因此，本文同样采取此方法来生成每一代的缩放因子[12]，并根据文献[13]设置缩放因子的取值范围为F∈[0.4，0.95]。

(4)交叉

采用交叉策略可以进一步增加种群多样性，常用的交叉方法有二项式交叉(Binommial Crossover)和指数交叉(Exponential Crossover)。本文使用的二项式交叉策略为：

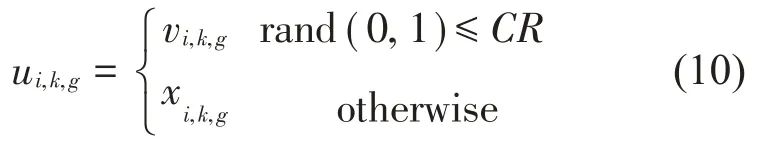
式中：ui,k,g为实验向量(Trial Vector)，下标分别代表第g代中第i个个体向量的第k维的值，k∈[1，D]，CR为交叉概率。

同理，采用JADE中的方法，使用柯西分布随机生成每一代的交叉因子[12]，并根据文献[13]设置交叉概率的取值范围为CR∈[0.8，1]。

(5)选择

选择策略是DE 算法的最后一步，将通过交叉、变异得到的实验向量与原始向量进行对比，对于求解本文中的最小优化问题，选择适应度函数更小的那一个向量进入下一代。可表示为：

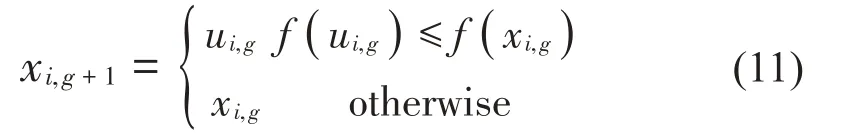
式中：f(xi,g) 代表第g代种群中个体向量xi,g的适应度函数值。

CNN-DE模型的设计流程图如图1所示。

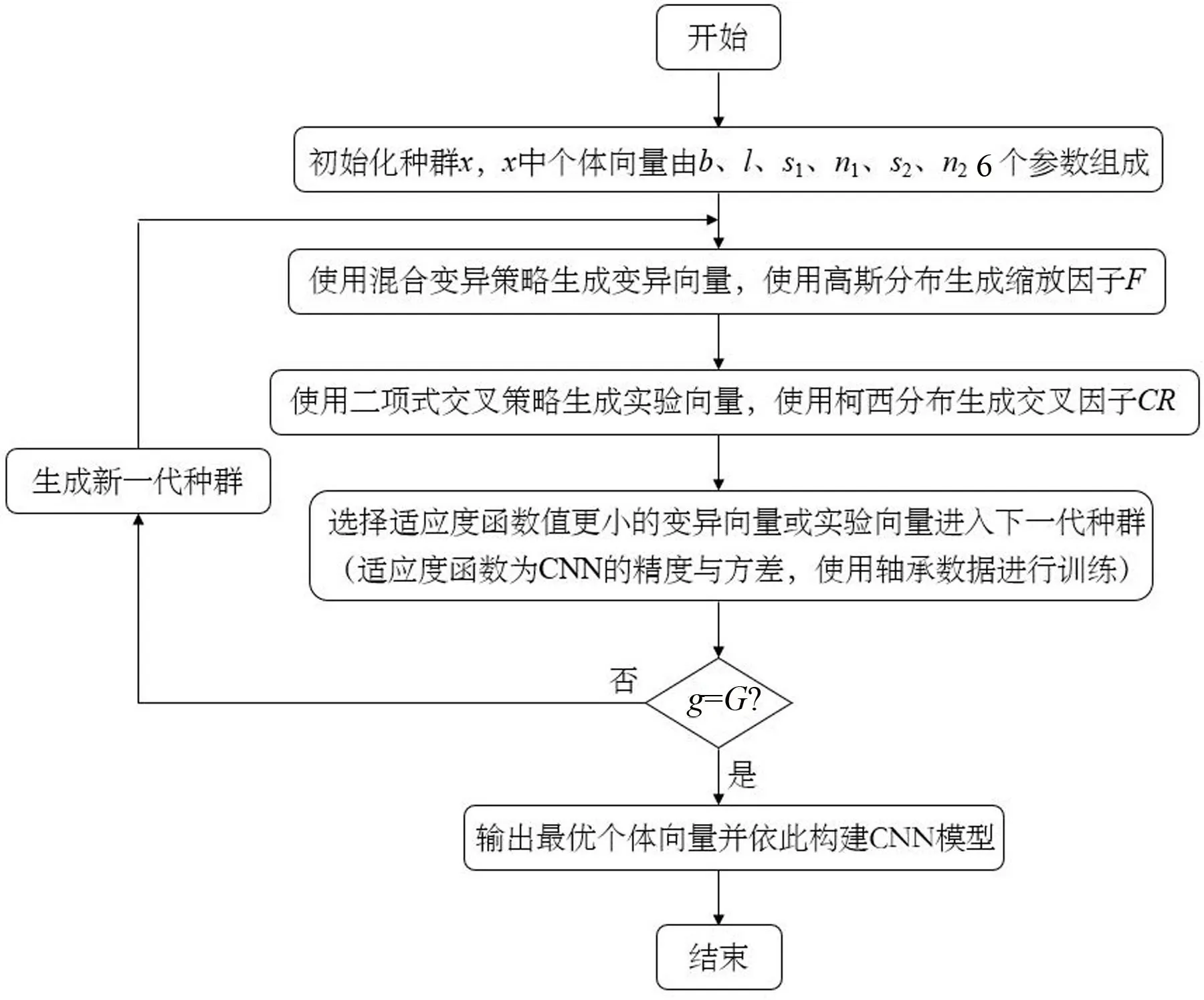
图1 CNN-DE算法流程图

3 滚动轴承故障诊断实验

3.1 数据来源

本文选用的故障诊断实验数据来源于美国凯斯西储大学(CWRU)滚动轴承数据中心。CWRU数据集是世界公认的滚动轴承故障诊断标准数据集，每年都有大量的学者使用CWRU 数据集来验证所提算法的有效性。CWRU 数据集中包括了采样频率12 kHz和48 kHz下的数据，加速度传感器放置于电机壳体的驱动端、风扇端和基座上。本文使用12 kHz 采样频率下风扇端轴承的运行数据，数据描述如表1所示。

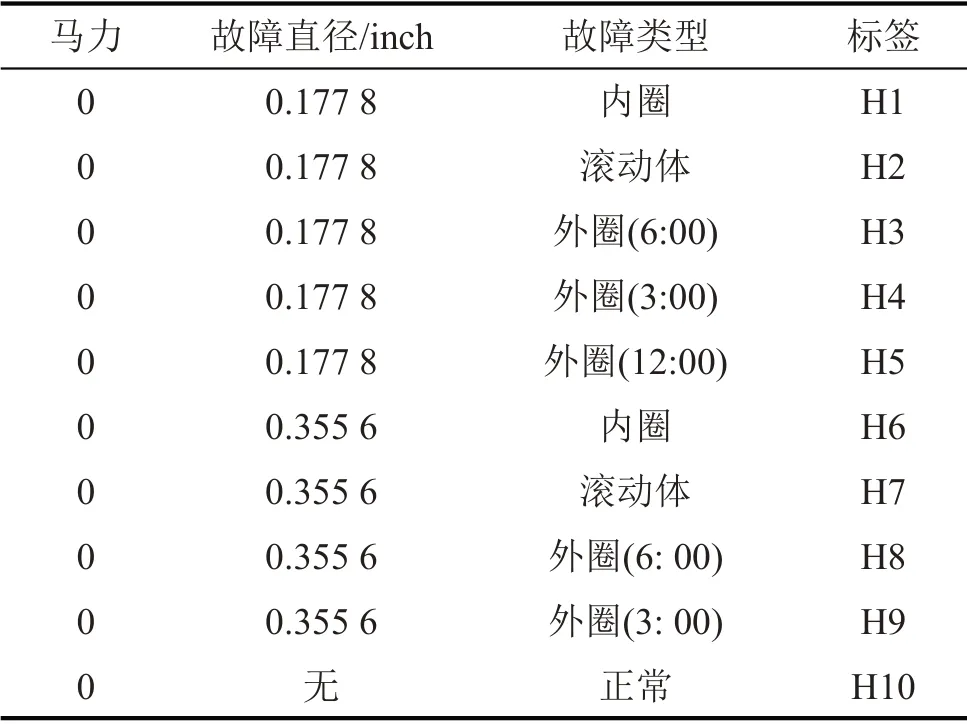
表1 数据介绍

本文使用的计算机配置为i5-9300HCPU，主频为2.4 GHz，内存为16 GB，编程软件为Python，使用Google公司开发的TensorFlow环境。

3.2 滚动轴承数据预处理

滚动轴承振动信号通常具有非线性和非平稳的特点，频率可变，而傅里叶变化是基于一个完整的信号周期定义的，故传统的傅里叶变化在处理此类信号时具有相当的局限性。

Huang所提出的模态分解方法能够根据信号本身的特点，自适应地将信号逐层分解成若干个内涵模态分量(IMF)，从而克服了傅里叶变化在频率上的局限性。同时，考虑到经验模态分解(EMD)存在的模态混叠问题[14]和集合经验模态分解(EEMD)存在的信号重构误差[15]，本文选用自适应噪声完备集合经验模态分解(CEEMDAN)对原始数据进行处理。CEEMDAN作为EMD和EEMD的改进算法，能够有效提高模态分解的精确度、完备性和运行效率。其分解的主要步骤如下：

设原始信号为x(t)，向x(t)中添加高斯白噪声gi(t)：

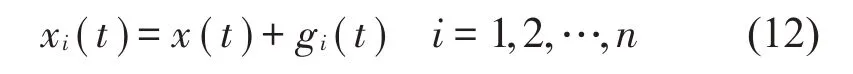
式中：gi(t)为第i次添加的高斯白噪声，n代表添加高斯白噪声的总次数，xi(t)为第i次添加的高斯白噪声与原始信号相结合而形成的合成信号。再使用EMD 对xi(t)进行分解。记经CEEMDAN 分解所得的模态分量为IMFCEEMDAN，有：

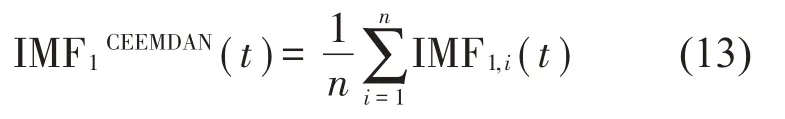
式中：IMF1CEEMDAN(t)为经CEEMDAN 分解所得的第一个模态分量，IMF1,i为第i次添加高斯白噪声时经EMD 分解所得的第一个模态分量。接下来计算其余量：

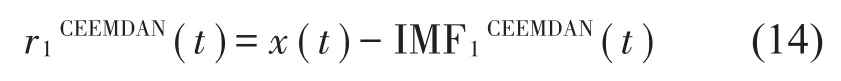
式中：r1CEEMDAN(t)为经CEEMDAN分解所得的第一个余量。重复上述步骤直至余量为单调函数或常数序列，从而完成CEEMDAN 分解，得到若干个IMF 分量。但并非所有的IMF分量中都包含着有效的故障信息。因此，需要对得到的IMF分量进行筛选。

峭度是用来描述波形尖峰度的一个统计学参数，也是滚动轴承故障诊断中最常用的参数之一，可用来表征旋转机械故障信号中冲击的大小[16]。当滚动轴承处于正常运行的状态时，其振动信号的幅值近似满足高斯分布，此时的峭度值约为3。当出现故障之后，大幅值振动信号出现的频率增加，从而导致高斯分布曲线出现偏斜或分散。此时，峭度值也会相应增大。因此，在一般情况下，峭度值越大，说明滚动轴承发生的故障越严重，也可以认为IMF 分量中所包含的故障信息越多。本文将峭度值最大的IMF分量筛选出来，并用作后续分析的数据。

峭度的计算公式为：

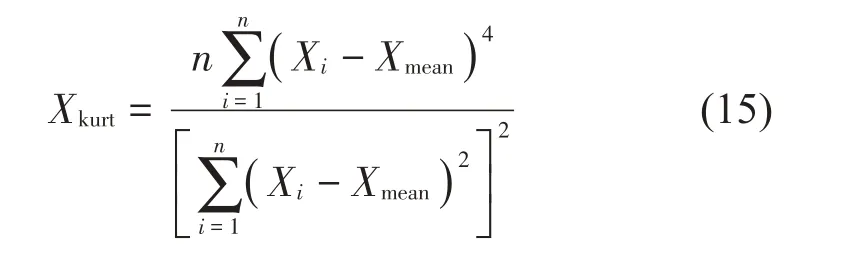
式中：Xi代表样本，Xmean代表样本在某个时间段内的平均值，n代表总的样本个数。

随着故障等级的提高，峭度值会逐渐饱和，其诊断能力也会随之下降。因此，为了进一步提高故障诊断的可靠性，需要采用多参数的故障诊断方法[17]。均方根属于有量纲参数，并且对于滚动轴承磨损类的故障比较敏感；峰值因子属于无量纲的参数，对于滚动轴承所发生的表面损伤类故障与磨损类故障都比较敏感。基于上述分析，本文将峭度、均方根和峰值因子一起作为特征进行提取，再使用CNN-DE 模型建立这些参数与滚动轴承各种不同运行状态之间的对应关系，从而实现故障诊断的功能。

均方根的计算公式为：

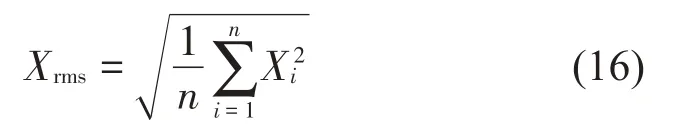
峰值因子的计算公式如下：

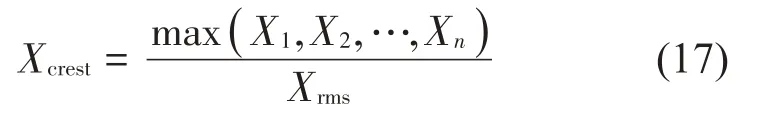
3.3 数据预处理效果

采样频率为12 kHz，采样时间为10 秒，以由基座加速度传感器所采集的风扇端轴承内圈故障数据为例，电机载荷为0，故障直径为0.177 8 inch，标签为H1，经分解得到的IMF分量如图2所示（仅使用前9个）。

图2 分解后的各IMF分量

再计算出各IMF分量的峭度值，得到图3。

观察图3可知，IMF2分量的峭度值最大，故选择IMF2分量作为后续分析的样本信号。

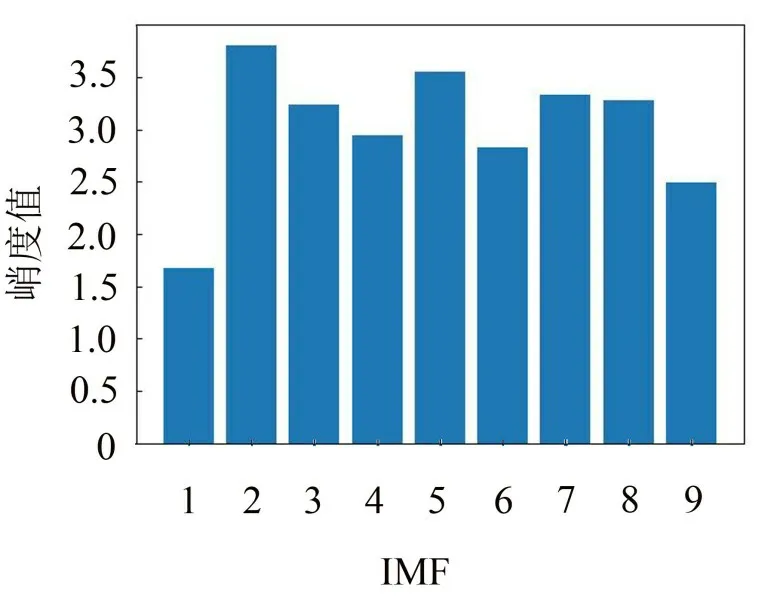
图3 IMF分量的峭度值

IMF2分量为列向量，长度为120 000。本文将IMF2分量重构为100×1 024 的信号矩阵(超出102 400 的部分舍去)，即样本个数为100，每一个样本由1 024 个连续采样的数据构成。再计算出每一个样本的峭度、均方根与峰值因子，从而构建出H1的输入矩阵，记为SH1100*3。重复上述的步骤，分别计算出标签为H2至H10的滚动轴承运行数据的输入矩阵，最后将得到的所有输入矩阵按行合并成S1000*3。

3.4 基于CNN-DE的滚动轴承故障诊断

随机划分S1000*3的70 %作为训练数据，剩下30 %作为测试数据。再使用CNN-DE、CNN 和BP 3 种算法进行故障诊断，算法的迭代次数设为200，其余参数与上文中设置相同。经过优化之后得到CNN-DE的参数和CNN设置的参数如表2所示。

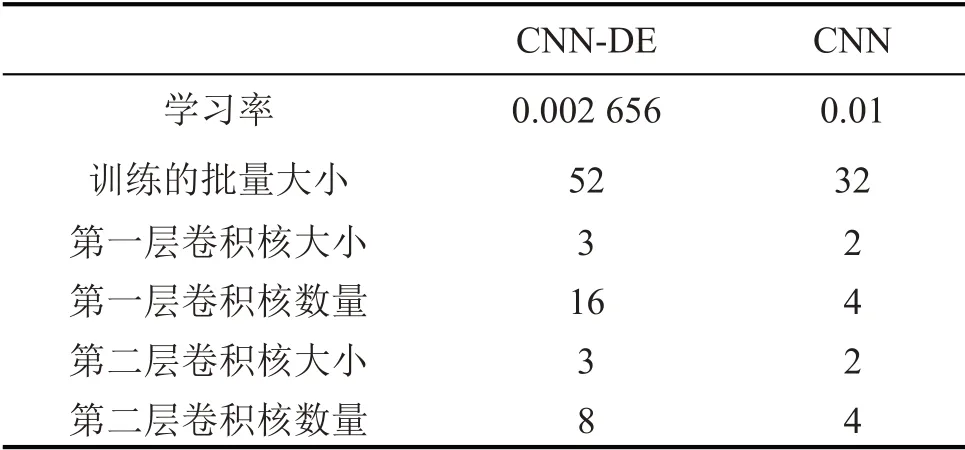
表2 CNN参数

为了更直观表现CNN-DE 算法的优越性，本文将CNN-DE 与CNN 的精确度函数和损失函数可视化，得到图4至图7。

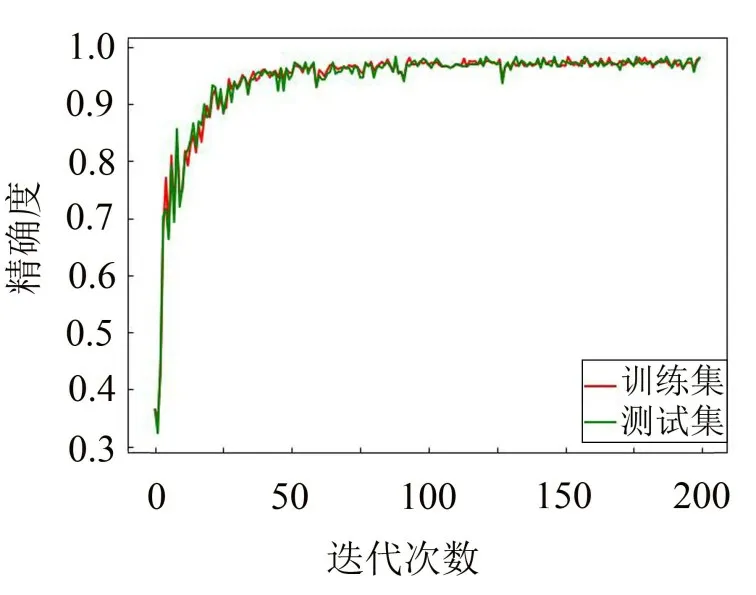
图4 CNN-DE的精确度函数

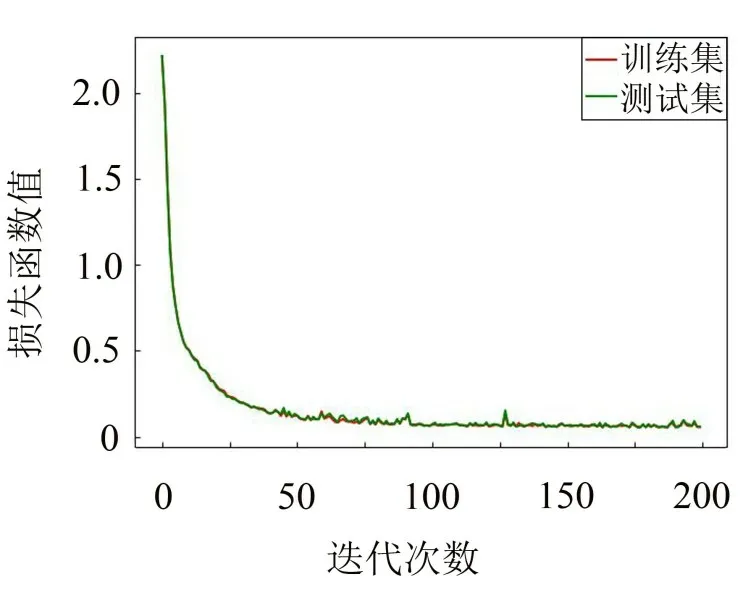
图5 CNN-DE的损失函数

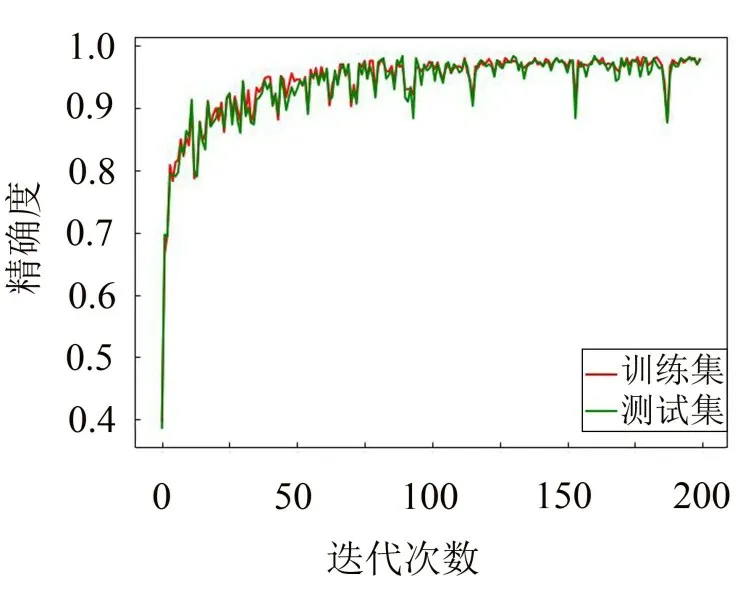
图6 CNN的精确度函数

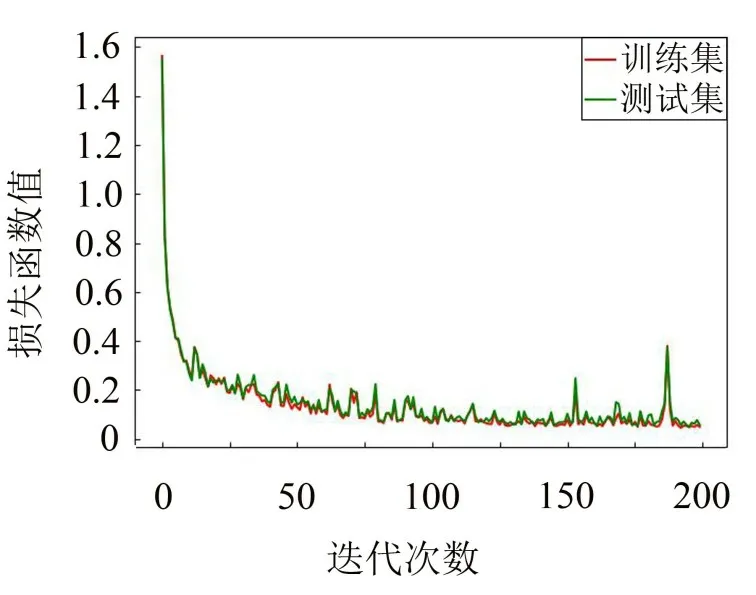
图7 CNN的损失函数

从图4至图7的对比中可以观察到，CNN-DE的曲线波动比CNN的曲线波动要平缓得多，说明本文提出的CNN-DE 模型很好提高了网络的稳定性，优化效果明显。

再将CNN-DE、CNN和BP 3种算法的诊断结果汇总，得到表3，其中不计算BP算法方差。

表3 诊断结果对比

在表3中可以观察到，标准CNN未经优化，网络的输出非常不稳定；而CNN-DE 算法稳定性相比CNN算法提升了一个数量级，诊断精度也要比CNN和BP更高。

为了进一步明确CNN-DE对不同类型故障的诊断能力，本文以混淆矩阵的形式输出诊断结果，如图8所示。

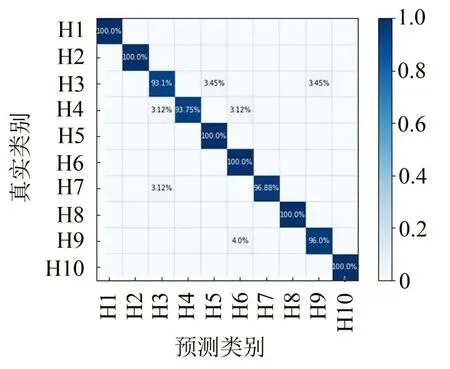
图8 CNN-DE故障诊断的混淆矩阵

观察图8可知，CNN-DE 针对H1、H2、H5、H6、H8、H10类故障的诊断精度达到了100%，对于其他类型的故障，CNN-DE的诊断精度也都在90%以上，最低为93.1%。说明本文提出的基于CNN-DE的滚动轴承故障诊断模型拥有良好的诊断能力。

最后，为了验证在噪声干扰的情况下CNN-DE的抗噪能力，本文在滚动轴承的原始振动数据中添加高斯白噪声，衡量噪声强弱的标准为信噪比SNR。本文设置3 组噪声实验，信噪比的取值分别为-10 dB、-5 dB 和5 dB，数据处理的方法同上文，再使用CNN-DE、CNN 和BP 3 种算法进行故障诊断，结果如图9所示。

由图9可知，无论是在强噪声干扰或弱噪声干扰的情况下，CNN-DE 的故障诊断能力都是3 种算法中最好的，说明CNN-DE有着良好的抗干扰能力，从而拥有更高的工程应用价值。

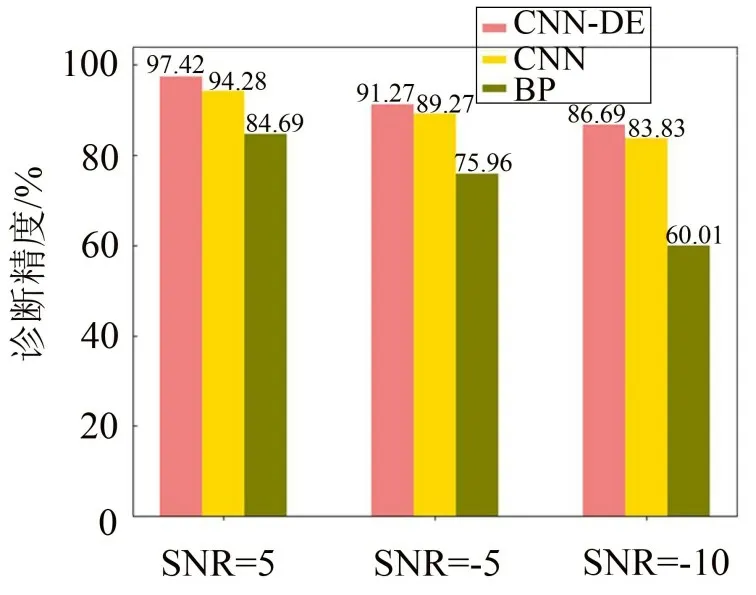
图9 噪声干扰下各个算法的诊断精度

4 结语

针对CWRU数据集，使用时域和时频域的方法对原始数据进行处理，提取出最有价值的信号特征。同时，为了使CNN 具有更好鲁棒性和精度，本文使用差分进化算法自适应调节CNN中最为重要的6个超参数，并且将CNN的精度与稳定性同时作为优化的目标。从对比结果中可以看出，本文提出的CNNDE 算法具有较高的故障诊断精度和较稳定的网络输出，在噪声环境下也能保持一定的诊断精度。下一步会针对自测数据进行故障诊断研究，从而进一步提高算法的工程应用价值。