基于PSO-LSSVM球磨机负荷参数预测及监测系统开发

罗小燕，黄耀锋，李波波，刘吉顺

(1.江西理工大学 机电工程学院，江西 赣州 341000；2.江西省矿冶机电工程技术研究中心，江西 赣州 341000)

磨矿工序中各设备质量的好坏直接关系到整个选矿厂的经济和技术指标[1－3]。球磨机是选矿生产中的耗能大户，研究发现[4]，球磨机能耗占整个磨矿流程能耗的30%～70%左右，磨机负荷状态是影响磨机能耗的主要可控因素。

球磨机的负荷状态与矿料和钢球的运动联系紧密，磨机转动时钢球撞击筒体产生的振动信号蕴含了负荷状态信息[5－8]，故在实际应用中常采用磨机筒体的振动信号来间接判断磨机的负荷状态。由于磨机工作环境复杂，筒体振动信号是一种非线性、非平稳、多耦合的信号[9－10]，且包含大量的噪声。因此，对筒体振动信号进行特征提取和负荷预测的研究一直是需要解决的热点问题。卿宗胜等[11]提出一种基于自适应VMD 和改进功率谱估计的球磨机负荷特征提取方法，利用自卷积窗能量重心法对本征函数进行处理得到功率谱，把功率谱作为支持向量机的输入，实现对球磨机负荷状态的预测。赵立杰等[12]提出基于正则化随机配置网络的球磨机工况识别方法，在随机配置网络的基础上提出带有L2范数正则化随机网络，有效避免模型过拟合的风险。Yang等[13]利用CEEMDAN 算法将筒体振动信号分解成IMF 分量，利用主成分分析法（PCA）降低敏感IMF分量精细复合多尺度熵(RCMDE)的维度。以RCMDE 作为输入，将磨机的负荷参数作为输出，建立自递归神经网络，实现对磨机负荷的预测。

LSSVM 将SVM 的不等式约束转化为等式约束，并选取误差平方和作为优化目标函数，使得二次规划问题转化为线性方程组求解问题，简化了计算的复杂性，提高了运算速度，LSSVM 在非线性系统建模方面更具有优势。

贺敏等[14]针对变工况问题引入多任务学习机制，利用多任务最小二乘支持向量机方法对磨机负荷参数进行回归预测。蔡改贫等[15]利用正向云发生器生成的云特征向量作为LSSVM的输入，以磨机负荷参数为输出建立了软测量模型。以上软测量方法都能够准确预测磨机的负荷参数，但以上的软测量方法大多数都是运用提前采集的振动信号在离线的情况下对磨机负荷参数进行预测，而没有实现磨机负荷参数在线监测。

基于上述分析，本文以Bond指数球磨机为研究对象，提取球磨机各负荷状态的有效IMF 分量样本熵值作为特征值，应用经PSO 优化后的LSSVM 算法构建球磨机负荷参数预测模型，开发基于Lab VIEW的球磨机负荷参数监测系统。分析该算法的复杂度并进行系统测试，验证该方法的有效性和实时性。

1 基本原理

1.1 最小二乘支持向量机算法

支持向量机理论[16－18]是依据统计学习理论发展而来的一种分类和回归工具，利用结构风险最小方式来有效提高机器学习的训练速度和训练结果，可为实现球磨机负荷在线监测提供重要前提。

具体的LSSVM建模过程如下：

给定样本{(xi,yi),i=1,2,…,m}，其中xi∈Rd为输入向量，yi∈R为输出值，m表示样本数量。建立高维特征空间的线性回归函数见式(1)：

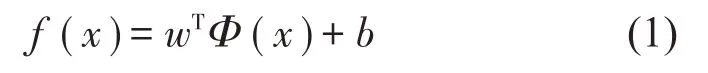
式中：w表示权值向量；Φ(x)表示非线性映射函数；b表示偏差量。

依据结构风险最小化原理，通过LSSVM优化后的目标见式(2)：

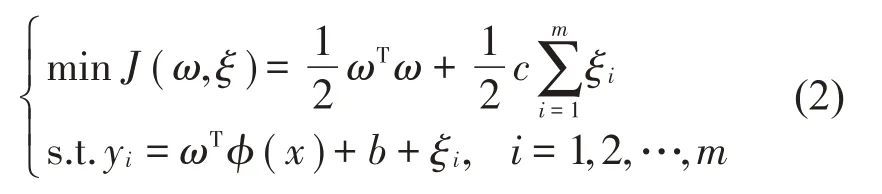
式中：ξi表示误差变量；c＞0 表示可变参数，用来平衡误差和减少模型复杂度，能提高所得函数的适用性及计算速度，引入拉格朗日函数，由式(2)可得式(3)：

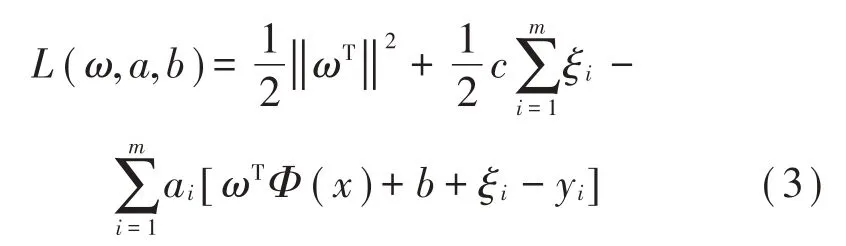
满足KKT条件是任何优化问题的关键，则有式(4)：

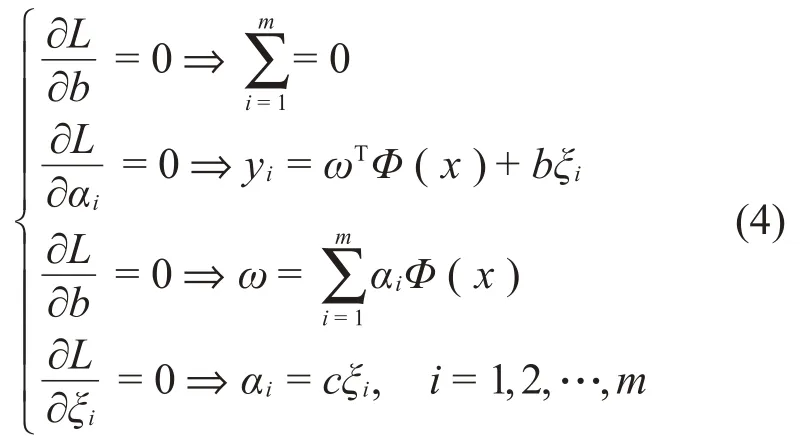
消去ω和ξi，式(4)可转化为式(5)：

在引入核函数K(xi,x)后LSSVM 回归估计可最终表示为式(6)：

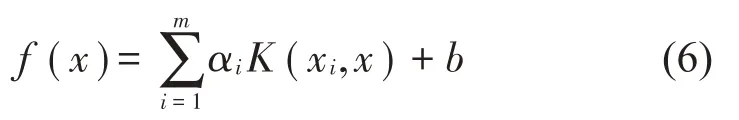
式中：ai和b由式(5)求出；K(xi,x)为核函数。径向核函数(RBF)拥有训练速度快、计算精度高等优点，为保证模型运算效率，采用RBF核函数来建立误差模型，表达式为式(7)：

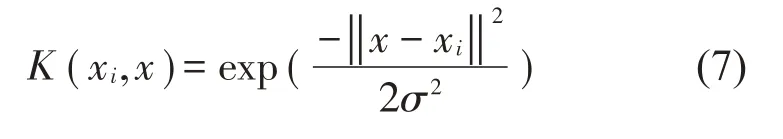
式中：σ表示核函数的宽度参数。

1.2 粒子群算法原理

粒子群算法(PSO)的基本原理[19－21]是模仿生物本能行为，通过优化得到一种基于群体智能的全局随机搜索算法。PSO 的具体运算过程如下：搜索G维空间中的m个粒子组成的种群U=(U1,U2,…,Um)，其中Ui=(Ui1,Ui2,…,UiG)代表第i个粒子的位置即第i个G维向量的解。利用目标函数求解粒子的适应度，若第i个粒子的速度为Vi=(Vi1,Vi2,…,ViG)，各粒子的极值分别为Pi=(Pi1,Pi2,…,PiG)，群体极值为Pa=(Pa1,Pa2,…,PaG)，表示粒子速度和位置的迭代公式为式(8)：

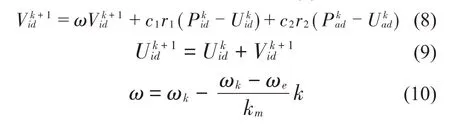
2 球磨机负荷参数预测模型建立

2.1 基于LSSVM的球磨机负荷参数预测流程

将自适应VMD 算法和Hilbert 边际谱样本熵理论应用于处理球磨机筒体振动信号，得到基于自适应VMD-Hilbert边际谱样本熵特征提取方法。特征提取过程如下：

(1)对采集到的筒体振动信号进行自适应VMD算法分解，得到K个IMF分量；

(2)选取相关系数大于阈值的IMF 分量作为有效分量。相关系数计算公式为式(11)：

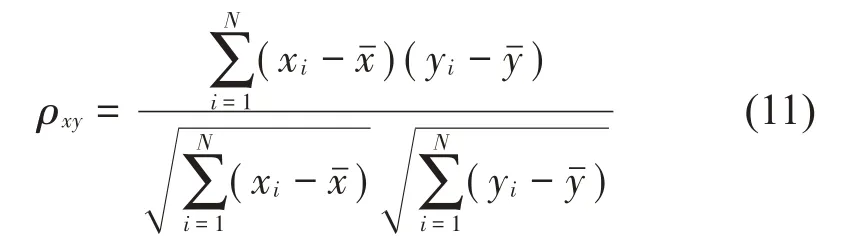
相关系数阈值计算公式为式(12)：

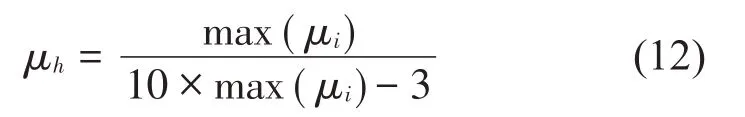
式中：μh与μi分别表示阈值和第i个IMF分量与原始信号之间的相关系数，去除相关系数小于阈值的分量。

(3)对由步骤(2)得到的有效IMF 分量进行Hilbert变换，再求解各IMF分量的边际谱样本熵。

(4)最后将各IMF 分量的样本熵组成的向量作为预测模型的输入量，料球比和填充率作为输出量。具体流程如图1所示。

图1 基于LSSVM磨机负荷参数预测过程流程图

2.2 基于PSO-LSSVM磨机负荷参数预测过程流程

PSO是通过迭代的方式来优化各种问题参数的算法，利用PSO 来对LSSVM 模型的参数进行优化，可以提高LSSVM 的识别准确率。基于PSO-LSSVM的球磨机负荷参数预测流程如图2所示。

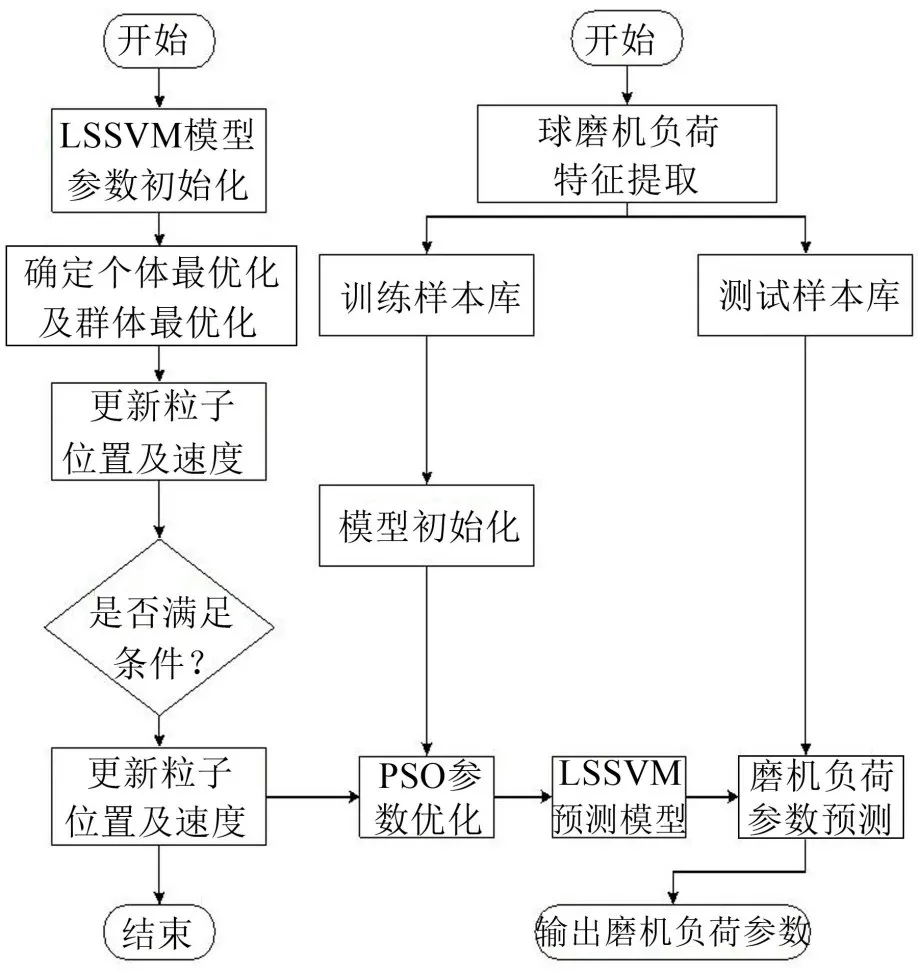
图2 基于PSO-LSSVM磨机负荷参数预测过程流程图

具体的PSO-LSSVM运算过程如下：

设训练样本为：

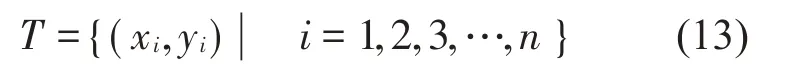
（1）假设最优回归函数如式(14)所示：

式中：ω为权向量，b为偏置量。

（2）再将求解最优问题替换为求解回归问题：

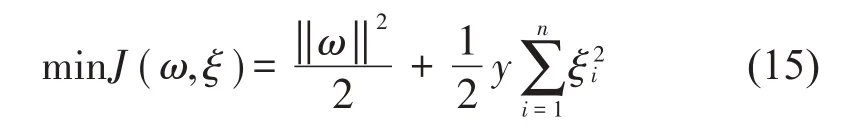
式中相对应的约束条件为：

式中：ξi为松弛因子，y为正则化参数。

（3）基于拉格朗日函数可得：

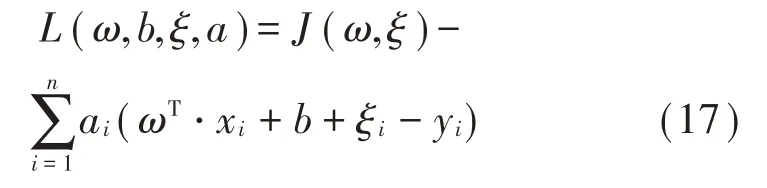
式中：αi为拉格朗日因子。

（4）将高斯径向基函数作为模型的核函数，见式(18)：

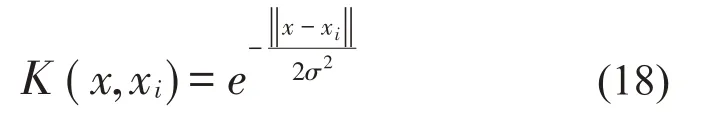
式中：σ2为核函数宽度。

（5）然后通过PSO 算法优化模型的正则化参数y和核函数宽度σ2，表达式为式(19)和式(20)：

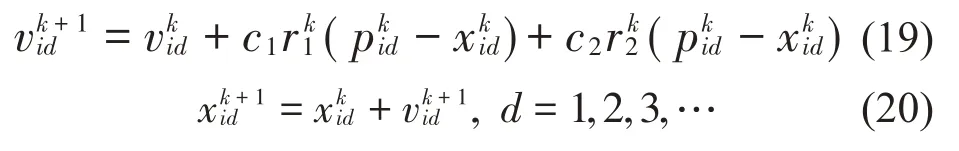
式中各参数的含义如表1所示。

表1 粒子群算法参数含义

（1）参数经过优化后的LSSVM 回归函数表达式见式(21)：

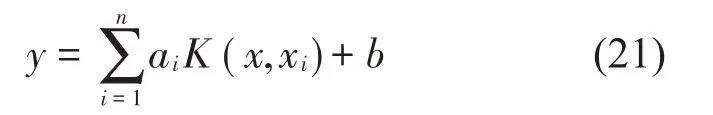
3 预测模型仿真分析

选取常用的GA优化算法和PSO优化算法进行比较，设置两者的原始参数如表2所示。

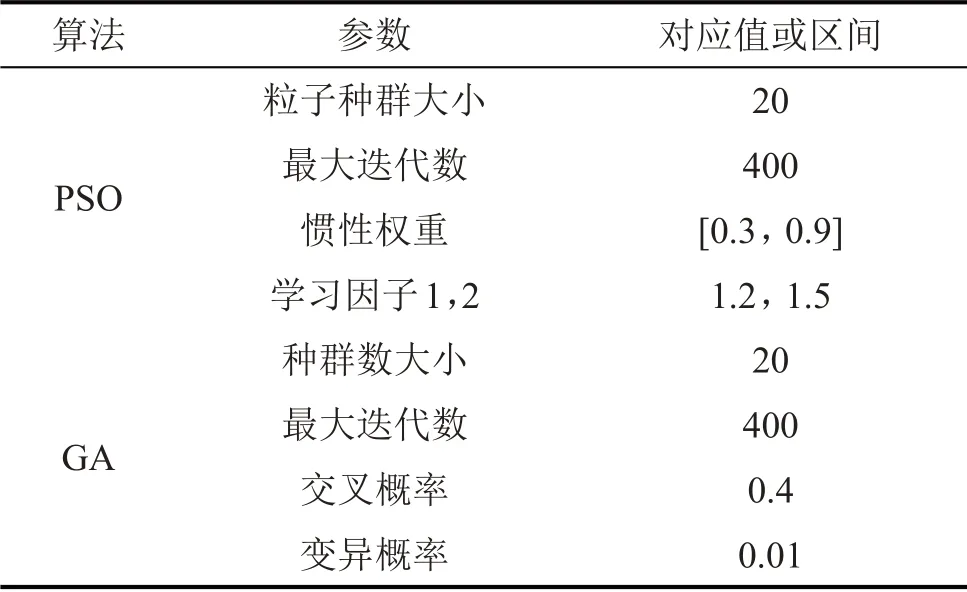
表2 两种优化算法初始参数设定

UCI 数据集常用于分析机器学习算法性能，为验证经不同算法优化后LSSVM预测模型性能差异，随机选取UCI 数据集中的两类数据进行模拟测试，数据集参数如表3所示。

表3 UCI标准数据集中的4类数据

模拟测试时将每类数据集分为5 份，运行10 次后PSO-LSSVM预测模型的预测值与实际值差对比如图3所示。

分析图3可知，PSO-LSSVM模型在模拟测试中预测误差相对较小，且不会有很大波动，符合基于UCI数据集对算法的测试误差要求。采用LSSVM、GA-LSSVM和PSO-LSSVM模型对相同数据集进行模拟测试，测试结果如图4所示。

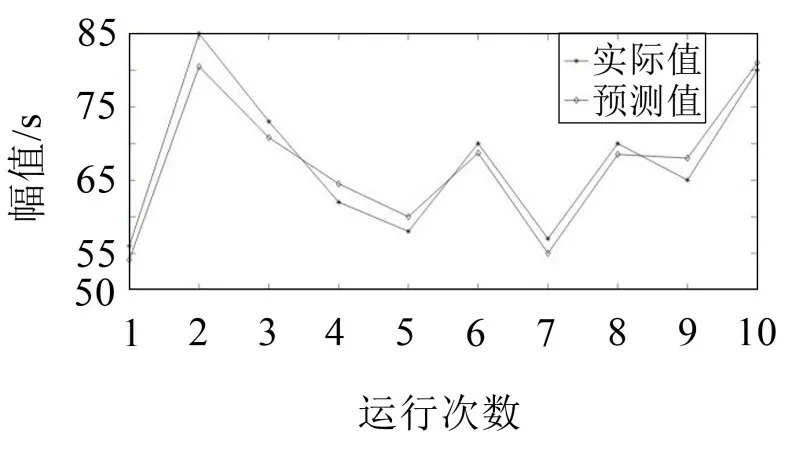
图3 基于PSO-LSSVM预测模型模拟测试曲线

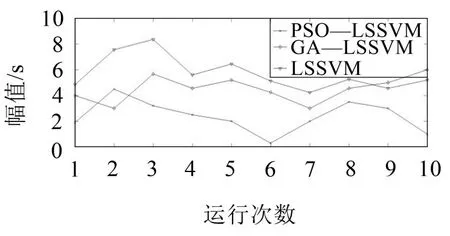
图4 不同模型预测偏差绝对值

由图4可知，相对于传统LSSVM 模型、GALSSVM 模型和PSO-LSSVM 模型的预测偏差绝对值，PSO-LSSVM 模型的预测偏差绝对值较小，证明了经PSO 优化后的LSSVM 模型有更高的预测精度。

4 球磨机负荷参数预测模型的实验验证

4.1 实验平台搭建

本研究选用实验室φ330×φ330 mm 的Bond 指数球磨机进行磨矿实验，采用NI 公司的NI ELVIS II+数据采集卡进行筒体振动信号采集。设计了磨机筒体振动信号采集系统，Bond指数球磨机及传感器安装位置图如图5所示。

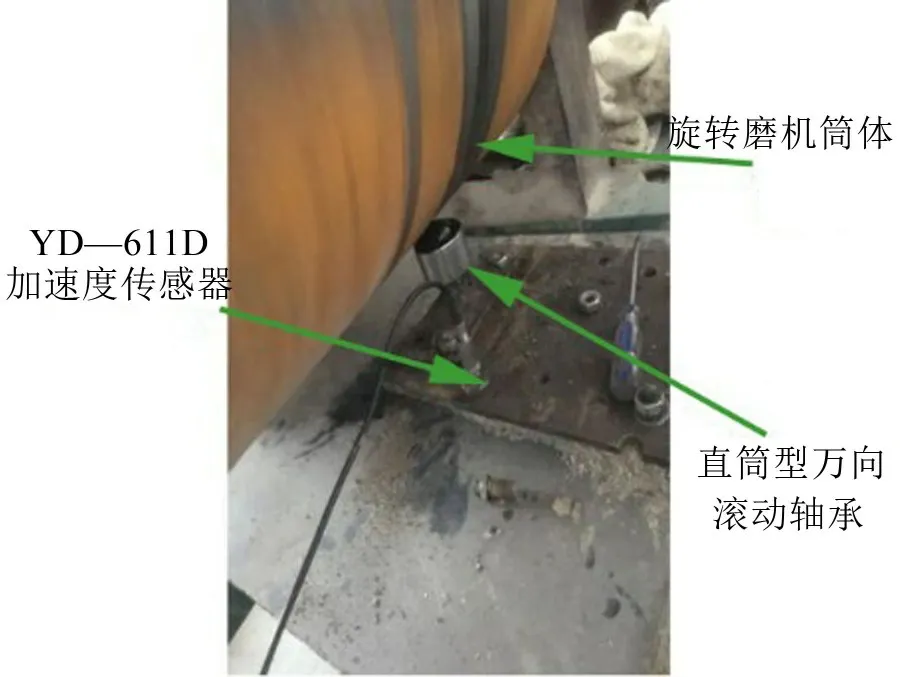
图5 Bond指数球磨机及传感器安装位置图

实验所用矿石物料主要为钨矿石，密度为1 800 kg/m3。实验前将物料筛分为5个等级，依次为2 mm～5 mm、5 mm～8 mm、8 mm～11 mm、11 mm～15 mm和15 mm～20 mm。选用φ20 mm、φ30 mm、φ40 mm、φ50 mm 等尺寸的钢球，其密度为7 800 kg/m3。共计有32 组实验数据用于建立离线情况下的预测模型，其中用实验数据的80 %训练模型，20 %验证模型。各组实验的工作状态参数如表4所示。

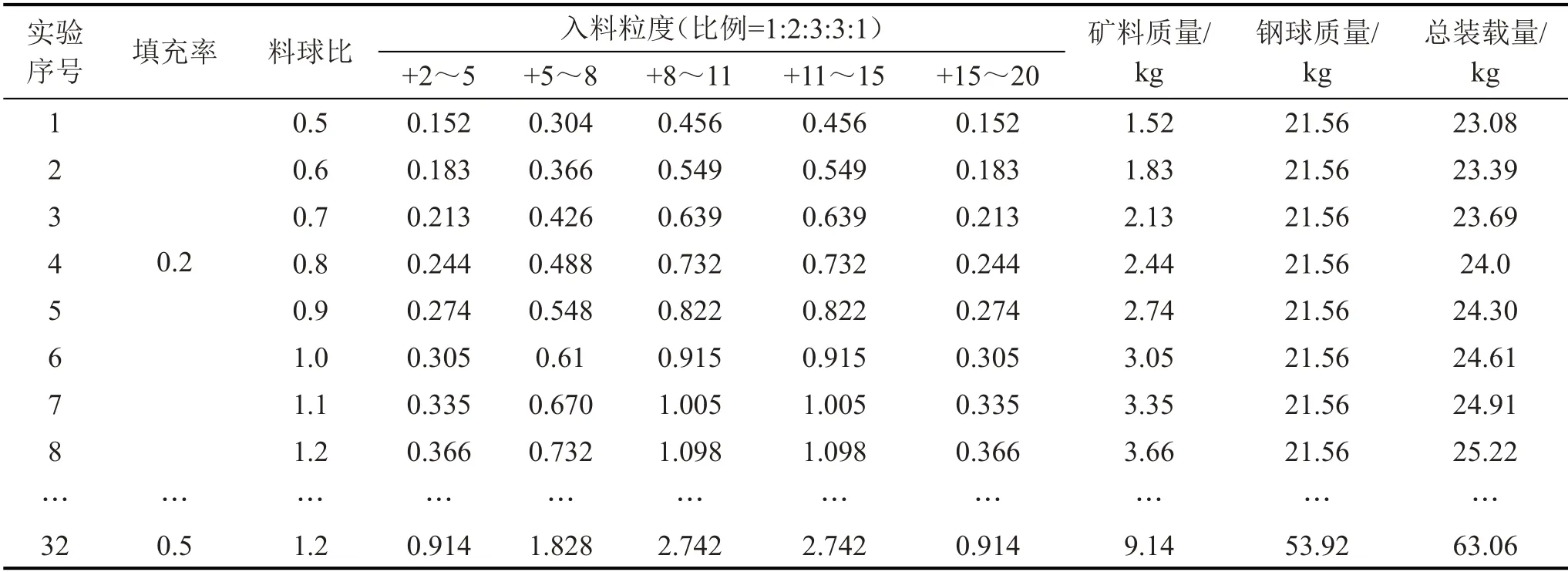
表4 各组实验的工作状态参数

4.2 预测误差评判指标

球磨机负荷参数预测是根据振动信号特征对同一时刻的球磨机负荷参数进行估算，由于振动信号存在噪声，因此预测值与实际值存在一定误差。为了量化算法的预测性能，采用均方根误差、平均绝对误差、绝对误差百分比作为预测误差的评判指标。其计算公式如下：

平均绝对误差定义为：

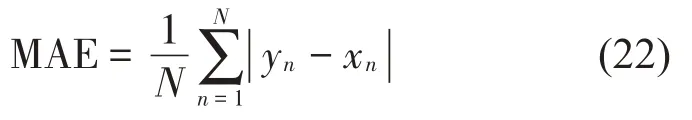
绝对误差百分比定义为：

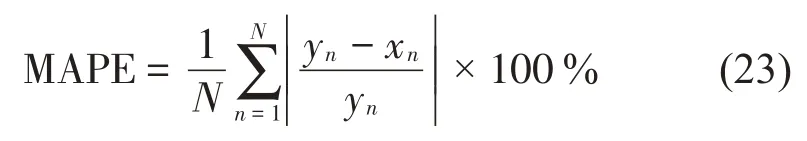
均方差定义为：

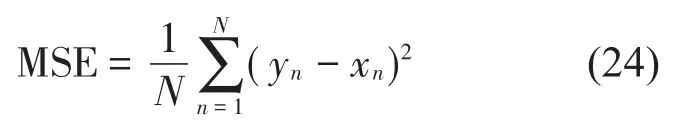
式中：yn表示实际值，xn表示预测值。

4.3 基于PSO-LSSVM的球磨机负荷参数预测模型的实验验证

为验证基于PSO-LSSVM 磨机负荷参数预测模型精度，对经过训练后的PSO-LSSVM 预测模型进行实验验证，预测值与实际值如图6所示。

图6 基于PSO-LSSVM球磨机负荷状态参数预测值与实际值对比图

分析图6可以得到，由基于PSO-LSSVM的球磨机负荷参数预测模型得到的球磨机负荷参数与实际值相差不大，总体上的预测精度较高。为进一步验证PSO-LSSVM算法准确性，利用传统LSSVM模型对磨机负荷进行预测，预测值与实际值对比如图7所示。

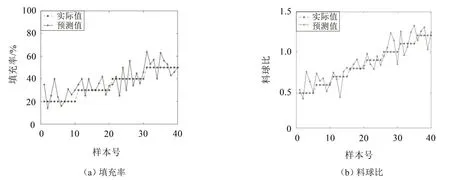
图7 由LSSVM模型所得预测值与实际值对比图

对比分析图6和图7可知，PSO-LSSVM 预测模型相比传统LSSVM预测模型精度有较大提升，预测值与实际值间波动变小，稳定性更高。计算由2 种预测模型所得磨机负荷参数预测值误差指标，如表5所示。

表5 由2种预测模型所得磨机负荷参数预测值误差指标

由表5可知，填充率平均绝对误差降低了0.05，平均绝对百分误差降低了8.09%；料球比平均绝对误差降低了0.04，平均绝对百分误差降低了2.76%，预测精度有较大提高，验证了PSO-LSSVM 预测模型在球磨机负荷参数预测方面的适用性。

5 球磨机负荷参数监测系统开发

5.1 球磨机负荷参数预测模型算法复杂度分析

为满足监测系统的实时性要求，选取算法的时间复杂度进行对比分析，使设计的信号处理算法和预测模型的时间复杂度都处于一定的范围内。算法的时间复杂度表示该算法程序运行时间随输入规模增加而增加的数量级，是影响计算效率的关键因素。求解算法时间复杂度的步骤为：

（1）明确算法程序中的基本语句，算法中执行次数最多的程序语句称为基本语句。

（2）确定基本语句运行次数的数量级，主要确保基本语句执行次数函数中的最高次幂准确即可，为方便计算可以忽略低次幂和最高次幂的系数，就可简化计算程序，主要得到执行次数函数的增长率。

（3）利用大O记号代表算法的时间性能。通过大O记号表示基本语句执行的次数的数量级。

通常时间复杂度有：常数阶O(1)、对数阶O(log2n)、线性阶O(n)、线性对数阶O(nlog2n)、平方阶O(n2)、立方阶O(n3)、指数阶O(2n)，输入端的规模越大，则时间复杂度越大，即算法的计算效率越低。各阶时间复杂的频次随输入次数增加的时间频次图如图8所示。

根据图8各阶复杂度对比分析可知，输入次数增加越多，不同阶次的时间复杂度的差距也会越大。分别对几个常用的振动信号处理算法的MATLAB程序进行分析可知，小波包算法的时间复杂度为O(n3)，神经网络的复杂度为O(2n)。分析PSO-LSSVM算法程序可知该算法的复杂度为O(n2)，相对于其他优化算法在处理大数据时时间复杂度增加速度较低，且运行时间在性能指标范围内[3]，表明了该算法可以用于球磨机负荷参数实时预测模型。

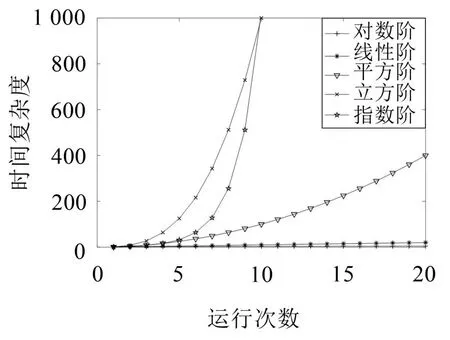
图8 各阶复杂度分析对比图

5.2 球磨机负荷参数监测系统设计

根据实际工程应用情况和磨机负荷监测需求，确立了整个系统总体设计构架如图9所示，该系统的主要功能有数据采集、信号处理与分析、用户管理等功能，通过人机界面可以方便地对填充率和料球比等负荷参数进行监测，运行该监测系统，其负荷参数预测的准确率如表6所示。

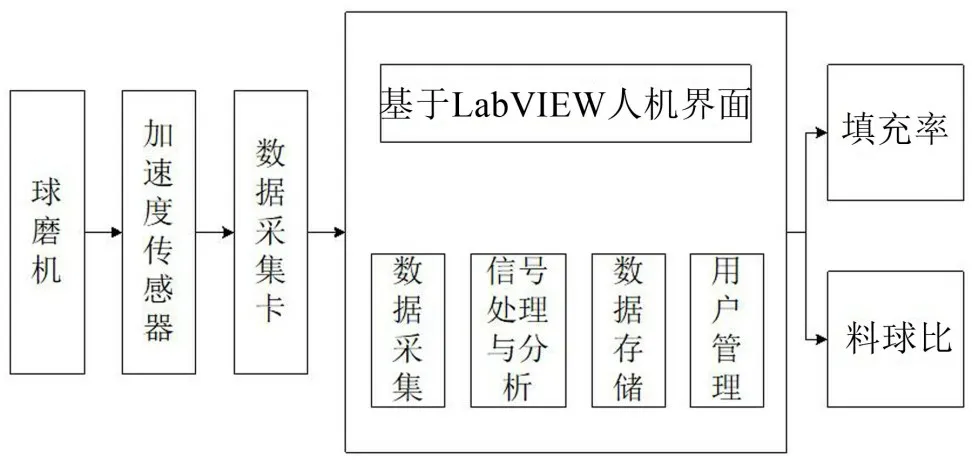
图9 球磨机负荷预测系统总体架构

表6 负荷参数预测准确率

由表6的数据可知，负荷参数预测模型对填充率的识别率较高，因为相比料球比的改变，填充率的改变对磨机筒体振动信号的影响较为明显。采用该监测系统预测共160 组负荷参数，其中预测参数在合理范围内的有103 组，即准确率为64.37%，相对于人工判断准确率的35%有较大提高[22]，系统单次计算时间均值为45 s/次。因此，该监测系统可以用于磨机负荷参数的实时预测。

6 结语

（1）构建了基于LSSVM 算法的球磨机负荷参数预测模型。为提高预测精度，利用PSO 算法对影响LSSVM 模型的径向核函数σ和核函数宽度γ进行优化，并通过UCI 数据集进行模拟测试，分析经PSO、GA优化后的LSSVM模型和传统LSSVM模型的类型识别准确度，表明优化后的LSSVM模型识别准确度更高，其中经PSO 算法优化后的LSSVM 模型识别准确率最高。

（2）分析得到该算法的时间复杂度为O(n2)，在处理大数据时其时间复杂度增加速度较慢，符合磨机在线监测系统的实时性能要求。

（3）对球磨机负荷参数预测系统的在线测试表明，基于LabVIEW的球磨机负荷参数监控系统准确率为64.37 %，相对于人工判断准确率的35 %有较大提高，实时性较好，可用于实际工程。