电机转子振动信号故障特征提取方法

申海锋，石 颉

(苏州科技大学 电子与信息工程学院 江苏 苏州 215009)

电机转子作为电机的扭矩输出机构，是电机的重要组成部分。一旦出现故障将直接影响电气系统的正常运行。通过对其运行状态的监测可以及时发现和清除故障。故障诊断是实现这一目的的有效工具，而特征提取作为其中最重要的一步，其有效性直接决定了诊断结果的准确性[1]。特征提取即提取对信号具有分类能力的特征，从而提高监测与诊断效率。

目前，针对电机故障的监测与诊断方法大多基于电流信号和振动信号[2]。基于电流的故障特征提取往往只能针对有限的电气故障，如转子断条，定子短路等。而电流在电机上的最终作用形式是转矩输出，振动信号中必将包含电气故障特征，故基于振动信号的故障诊断方法在工程现场被广泛使用。

振动信号的振幅、频率、轴心轨迹等均能反映出故障的特征[3]。在使用相关性分析和傅里叶变换等常用方法进行信号特征挖掘时，在非线性非周期性信号的分析和处理过程中只能提取到时域或频域的特征，会丢失大量信息。因此需要采用时频域分析方法提取更多、更能反映故障特征的有效信息，如小波变换、经验模态分解(Empirical Mode Decomposition，EMD)[4－5]等技术已经被成功应用于复杂信号的分析。此外，融合不同方法优势的混合技术研究也受到越来越多的关注。例如，将小波包变换(Wavelet Packet Decomposition，WPT)和希尔伯特变换相结合提出的希尔伯特-黄变换(Hilbert-Huang Transform，HHT)用以检测故障的特征频率，结果表明，该混合技术表现出了比传统小波包变换更好的性能[6]。多重信号分类与粒子群算法(Particle Swarm Optimization，PSO)、最小二乘法、模式搜索等算法结合用以提取故障特征可快速确定全局最优点[7]。

电机系统输出的力矩常受负载变化影响，某些故障的振动信号将表现出非平稳和非线性特性[8]。小波变换在信号分析时可以通过时间窗口的选择对这一现象进行改善，但如何确定合适的小波基和分解层数是一个重要的问题。另一方面，小波变换过程中小波基选择后是确定的，不能根据信号特征在分解过程中自适应调整[9]。与小波变换不同，经验模态分解是一种自适应处理技术，可根据信号的固有特性进行分解，适用于复杂信号的分析[10]。虽然，经验模态分解避免了分解层数和小波基的选择，且具有多分辨率分析能力，但是，当信号中存在突变或干扰时，将丢失部分时间尺度，导致严重的模态混合现象[11]。模态混合作为EMD中存在的重要问题，其改进方法一直是当前的研究热点之一。在众多的改进算法中，集成模态分解(Ensemble Empirical Mode Decomposition，EEMD)是一种对噪声友好的方法，因其对模态混合的抑制能力而闻名，目前已成功应用于轴承、齿轮箱等旋转系统故障信号分析中[12－13]。

为了度量信息源的确定性，1948年Shannon 提出了信息熵的概念[14]。然而，信息熵在度量信息源不确定性时仅考虑事件发生的客观概率，无法描述主观意义上对事件判断的差别。为了把主观价值和主观意义反映出来，Guiasu 引入加权熵的概念[15]。为了表征信息随时间动态变过程，样本熵[16]、模糊熵[17]和置换熵[18]被分别提出用以估计不同尺度上信息序列的动态特征。作为一种很有前途的工具，熵被广泛应用于特征提取、权重分析、不确定性度量、差异性评价等场景。

鉴于转子故障信号的复杂性，现有方法尚存在特征提取信息缺失，需人工确定基函数等问题。为了改善上述问题，提高特征提取的稳定性，保证故障识别的准确度，本文提出了一种基于EEMD 分解和权重熵尺度变换的转子故障特征提取方法。该方法以EEMD 为基础，对根据EEMD 分解得到的固有模态函数(Intrinsic Mode Function，IMF)提取标准差后进行权重熵变换，得到用于故障识别的特征向量。通过EEMD分解解决了特征提取时信息缺失和人工确定基函数的问题。权重熵尺度变换提高了样本的类间差异。实验结果表明，该方法具有更好的应用效果。

1 集成经验模态分解

1.1 经验模态分解

经验模态分解是一种自适应算法，它可以根据信号本身的特征分解成一系列的IMF。IMF应满足两个条件：

(1)极值的数量和过零点的数量必须相等或最多相差一个；

(2)在任意一点上，由局部最大值定义的包络和由局部最小值定义的包络的平均值为零。

对于给定的信号x(t)，经验模态分解法首先提取局部极值形成上下包络，再分别对局部极大值和局部极小值进行插值。然后计算上包络的平均值m(t)，并根据h(t)=x(t)-m(t)从信号中减去该平均值。信号x(t)被h(t)替代并重复上述两个步骤，直到h(t)满足IMF 的两个条件，则该过程结束。残差r(t)定义为r(t)=x(t)-h(t)并视为由上述步骤持续分解所得的新信号。如果残差满足停止标准，则分解过程结束。原始信号x(t)最终将被分解成多个IMF和最终残差，如式(1)所示。

虽然经验模态分解可根据信号固有特征进行自适应调整，但其具有两个重要缺陷：

(1)样条拟合方法的过冲或欠冲可能导致较大的误差，进而影响IMF的结构；

(2)如果信号存在突变或扰动，经验模态分解将丢失部分时间尺度，进而造成严重的模态混合。

1.2 集成经验模态分解

集成模态分解算法(EEMD)是一种解决EMD中模态混合问题的有效改进算法[19]，其运算步骤如下：

Step1：向目标信号中添加等级为L的随机白噪声n(t)：s(t)=n(t)+x(t)；

Step2：用EMD 对复合信号s(t)进行分解，得到一系列IMF；

Step3：重复步骤1、2共N次，但每次添加不同的白噪声信号；

Step4：计算对应IMF的平均值作为最终结果。

其中，白噪声强度等级L以及重复次数N是决定EEMD 分解效果的两个关键参数，根据文献[20]中所论述的方法，以分解误差作为衡量指标进行确定。当L=0.2,N=100 时，EEMD 对振动信号分解效果最好。

1.3 EEMD应用于电机振动信号

为验证EEMD 相对于EMD 在信号分解时的优势，对5组实际采集的电机转子振动信号进行分解，同时采用均方根误差(RMSE)、平均绝对百分比(MAPE)、纳什系数(NSE)作为分解准确性的评估指标，3种误差评价指标的计算方式如下：

其中：y为原始值，yi为分解值，n为原始值个数，yˉ为n个原始值的平均值；NSE ≤1，且越接近1，分解精度越高。EMD 与EEMD 分解效果如表1所示，对随机选择的5 种电机转子振动信号分别进行EMD 和EEMD 分解，在3 种不同评价指标下，EEMD 的分解精度及稳定性均远高于EMD。

表1 EMD与EEMD分解效果比较

1.4 故障特征提取和权重熵变换

特征提取的目标是根据给定样本集确定一个能够表征样本间差异性的特征向量使得样本可以被正确地分类[21]。振动信号中包含着大量表征电机转子状态的信息，可从中提取特征向量用于状态分类。然而由于振动信号具有复杂的非平稳、非线性特性，虽然EEMD已经自适应地将信号分解成不同频域内的IMF，但其特征仍不明显，无法直接用于表征电机的运行状态。因此我们需要进一步从IMF中提取故障特征。

EEMD分解的核心思想是通过向待分解信号添加白噪声消除模态混合现象，因此IMF 本身已具有抗噪声特性，无需在特征提取时进行滤波操作。IMF的本质是对信号减法求异所得的一系列频率相近的包络信号，表征着信号与基波的偏离程度。而方差可以衡量一组数据的离散程度或度量信号在一段时间内的偏离程度。因此采用方差对IMF进行描述在工程应用时是合理的。

IMF 方差取值区间为[0,1]，若直接将其作为特征值构成表征电机状态的特征向量，会导致表征空间内会出现局部堆积现象，使得具有明确差异的特征向量有着极高的相似性。故应首先对方差进行对数变换，扩大特征向量的表征空间。为进一步提升特征向量对电机状态的区分能力，受信息论和决策树的启发，本文提出了一种权重熵空间尺度变换方法，该方法通过熵值对特征进行权重变换来扩大样本的类间差异。

假设给定分类样本集D={(X1,Y1)，(X2,Y2),…,(XN,YN)}，其中Xi=(x1,x2,…,xn)为输入样本，(Xi,Yi)的特征向量，Yi属于{1,2,…,k}为样本分类标记。具体计算步骤如下：

1.计算数据集D的经验熵H(D)：

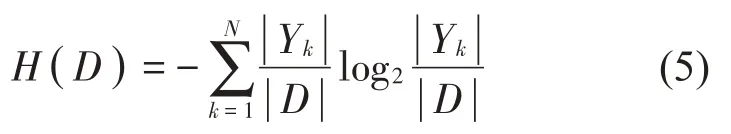
2.计算特征xi对数据集D的经验条件熵H(D|A)：

3.计算权重熵：

4.根据权重熵对特征值进行加权变换：

如果利用一个特征进行分类，其结果与随机分类的结果差异较小，则认为这个特征对分类效果的贡献极小。在经验上弱化这些特征，对分类精度的影响不大。相反，权重熵就是一种很好衡量特征对样本分类效果贡献度的指标。通过权重熵对特征值进行尺度变换可以扩大样本的类间差异或空间距离，提高样本分类或聚类的精度。这对于类间特征向量差异较小的样本无疑是一种很好的处理方式。

2 实验分析及讨论

2.1 数据集介绍

本文采用武汉大学公开的转子故障实验数据集进行分析和讨论[22]。实验中共设置了4种转子状态，即：转子正常、转子偏心、转子不平衡、转子断条。

转子偏心故障通过使用故障轴承模拟电机转子轴心不对中来实现。转子不平衡故障通过在转子笼质量盘边缘的螺丝孔内旋入一个2 g 的螺母模拟电机转子质量轴线与旋转轴线不重合来实现。通过对转子条进行打孔破坏模拟转子条断裂故障。采用GTS3-TG系列传感器进行振动信号采集，并将其传送至计算机进行分析和存储。对每种状态进行45次重复实验，每次实验时记录1 s采集的平稳振动信号组成用于分析的数据集，各状态的信号波形如图1所示。

图1 转子在4种状态下的振动信号

2.2 数据分析及讨论

从数据集中随机选取4种状态下的一组振动信号，按图2所示流程进行分析。首先采用EEMD 分解方法对4 种类型的信号进行分解，并按照信号频率将IMF由高到低进行排序，如图3所示，计算不同固有模态函数的方差。将每组固有模态函数的方差作为一个信号特征，构成输入特征向量。将其对数化后计算特征向量的权重熵，获得特征值的加权权重。按照权重对初始特征向量进行空间变换形成用于状态识别的特征向量。

图2 振动信号分析流程图

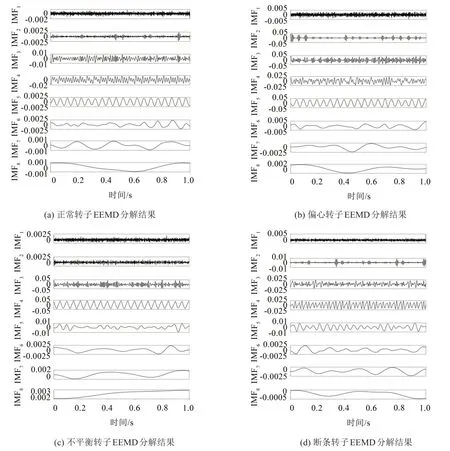
图3 4种状态下经EEMD分解所得的IMF信号

在转子断条数据集中随机选取其中的0.5 s 按照上述流程进行分析，得出他们的权重熵如表2所示。从表中可以看出对于在不同时间段采集的振动信号数据集，权重熵对特征重要性的排序未发生变化，通过权重熵进行特征重要性衡量具有很好的稳定性。

同样在转子断条数据集中分别选取时间窗口为0.25 s、0.5 s、0.75 s、1 s，按照上述流程进行分析，得出他们的权重熵如表3所示。其中，特征值X1至X8为按频率降序排列的IMF 的方差。从表中可以看出，对于在不同长度时间窗口采集的振动信号，权重熵对特征重要性的排序未发生变化。由此可见，通过EEMD分解信号进行故障特征的提取不受时间窗口的影响，无需人工确定基函数，具有很强的自适应性。根据表2和表3所示在不同时间段及不同时间窗口得到的权重熵，取其联合平均数，可得其分别为0.091 2、0.161 4、0.225 2、0.269 6、0.208 7、0.025 7、0.011 0和0.006 4，为本方法最终确定的权重熵。进一步分析经过权重熵加权变换后的特征向量的类内差异和类间差异。考虑到经过加权变换后的特征向量对应的特征空间已经发生了变化，存在尺度不一的现象，此时如果选取一般的欧氏距离法测算样本间的空间距离显然是不合适的。因此，在原特征空间选取X0=[1,1,1,1,1,1,1,1]的矢量模作为基准，在变换后的特征空间选取X′0=[0.091 2,0.161 4,0.225 2,0.269 6,0.208 7,0.025 7,0.011 0,0.006 4]的矢量模作为基准，采用各空间内特征向量矢量模与基准的比值作为衡量空间变换效果的指标。随机选取3组数据，其中1个作为基准向量，其余为样本，分析样本到基准向量的加权欧氏距离。如表4所示，X2、X3经变换后所得的特征向量X′2、X′3与基准向量X1'间的加权欧式距离约为原特征空间中X2、X3与X1的两倍，从中可以看出经权重熵变换后的样本类间差异被明显放大。

表2 不同时间段数据集特征值对应的权重熵

表3 不同时间窗口下数据集特征值对应的权重熵

表4 权重熵变换前后样本距离比较

传统的分类算法采用的是监督学习模式，依赖于人工对样本集的选择。为证明特征提取对样本的表征能力，本文采用无监督学习模式，通过不同的聚类算法对经过权重熵加权变换的特征向量进行聚类，EEMD 权重熵变换聚类准确度如表5所示。为进一步验证所提方法的先进性，分别与根据未经权重熵变换的EEMD、FFT-PDS分析、离散小波分析提取的故障特征进行对比实验。根据文献[23]的描述，选择小波法的最佳参数：小波基为db8，分解层数为3。根据不同方法提取特征的聚类准确度结果如表5所示。基于EEMD权重熵变换的聚类效果不管是对于单个聚类算法还是在整体平均准确度方面的表现都是最好的，与表中所列其他方法相比准确度平均提高了20.36%。而根据其他方法提取的特征向量准确度在不同聚类算法上的准确度波动较大，甚至出现了失效的情况。失效现象的出现可能是因为EEMD 分解出现模态混合，FFT-PDS 仅提取了信号的频域特征，小波分解的小波基在不同信号下的时间窗口不一致。这些问题导致了特征提取的片面性，使得不同聚类算法的表现出现巨大的偏差。

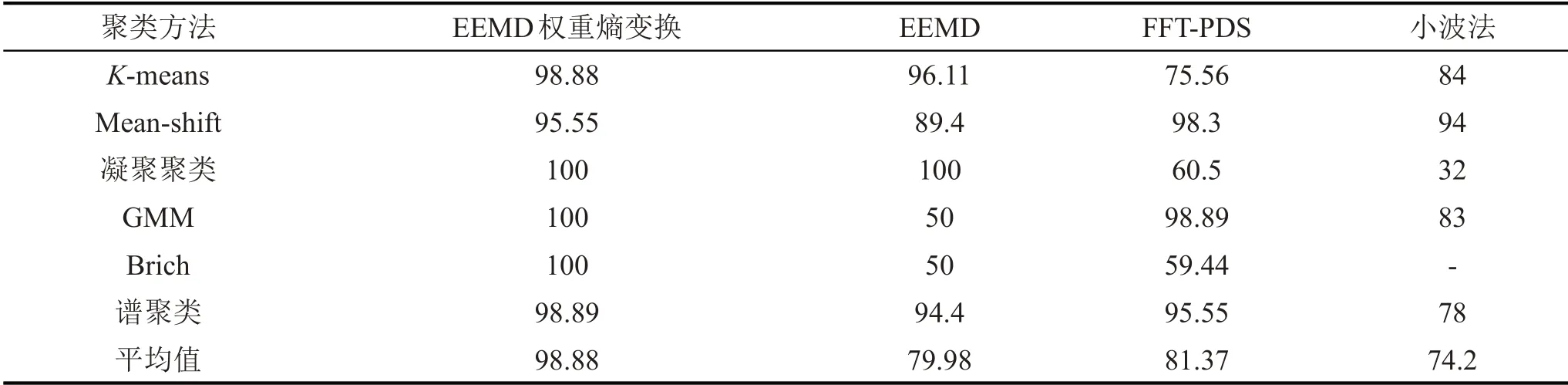
表5 不同方法提取特征的聚类准确度/(%)

为验证本方法的普适性，分别选择MAFAULDA 数据集中的径向、轴向和切向振动信号进行测试。经本文方法处理得到的特征向量在不同聚类算法下的结果如表6所示。同一位置的振动信号聚类结果波动平稳，没有出现明显的差异。不同位置信号聚类效果的平均值接近。结果表明本文所述转子振动信号故障特征提取方法具有很好的泛化能力。

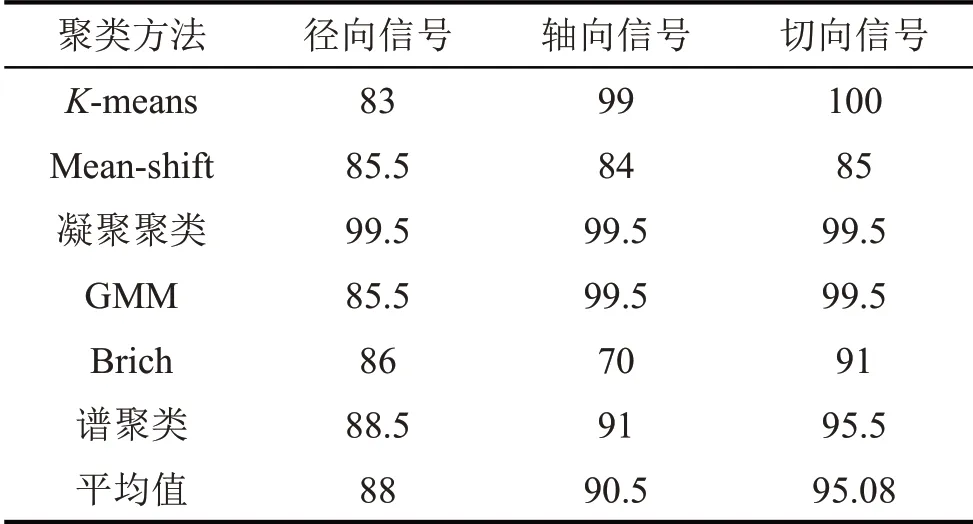
表6 本方法在MAFAULDA数据集上的表现/(%)

3 结语

本文从电机转子状态监测的实际需求出发，提出了一种使用EEMD 分解振动信号，以IMF 的方差为初始特征，通过对数化和权重熵变换进一步扩大特征间区分度的故障特征提取方法。同时通过对实际电机进行改造构建了4 种状态下的转子数据集，以实验数据集为基础验证了使用本方法的可行性及提取故障特征时的高区分度，并通过与现有特征提取手段比较，证明了本方法具有更高的准确性。

将EEMD分解技术成功应用于电机转子的故障特征提取，解决了以往通过时频域进行特征提取时需要人工确定时间窗口和基函数的问题。

将权重熵用于衡量特征值在表征电机转子状态时的重要性，并将其应用于特征向量的空间变换，提高了不同特征向量间的区分度。

采用所提出的基于EEMD分解和权重熵变换的故障特征提取方法，能够实现对电机转子的状态监测，相比其他方法有效提升了故障诊断的准确度。