欠定无人机发动机开车声音信号盲源分离

唐铭阳，吴亚锋，周 楠

（西北工业大学 能源与动力学院，西安 710129）

无人机是一种集航空、电子等多学科知识于一体的高新技术系统，近年来发展迅猛，并且广泛应用于军事、民用和商业等领域[1]。与之相应，对无人机发动机的安全性和可靠性的要求也越来越高，及时地发现和监测其故障，有着非常重要的意义和价值。但是目前国内发动机工程上应用的状态监测与诊断技术还较为落后[2]，传统的信号分解和提取技术很难为故障诊断提供有效的数据支持。盲源分离技术可以弥补传统信号分析方法的不足，并且可以与FFT方法进行综合运用，为发动机故障诊断提供了一种新的思路。

盲源分离(Blind Source Separation，BSS)是指在信号的理论模型和源信号无法精确获知的情况下，从混叠信号（观测信号）中分离出各源信号的过程[3]。其起源于20世纪80年代中期两位法国学者Taleb和Jutten的开拓性研究[4]，于1990年进入了高速发展的时期，并成为了时下最热门的数字信号处理研究内容之一。目前盲源分离在图像处理、移动通信、语音信号处理、地质勘探、医学工程等方面获得了成功的应用。国内对盲源分离的研究起步较晚，特别是将盲源分离技术应用到机械信号分离中是近些年发展起来的，许多高校也已积极投入到振动信号的盲源分离理论研究和工程应用中。

发动机在发生故障时伴随着异常声音的出现，盲源分离技术对此类声音信号的处理和分析，可以为进一步的发动机故障定位和诊断提供了必要的数据基础，并且与对振动信号[5]处理相比，声音信号传感器的布置相对简单，设备损耗也降低了许多，信号获取相对容易。基于此，本文提出了一种基于EMD-NLPCA 的欠定非线性盲源分离算法，并且将该算法应用在无人机发动机开车声音信号的分离上，获得较好的效果。

1 无人机发动机及其测试系统

1.1 无人机发动机简介

本文以某型四缸二冲程发动机为研究对象。该发动机为小型射空四缸水平对置风冷二冲程汽油发动机。进气系统采用两个膜片式化油器，并由笛簧阀控制进气，燃油系统采用两个膜片式燃油泵，点火系统采用CDE无触点磁电机，发动机通过外接电动机起动。其主要参数如表1所示。

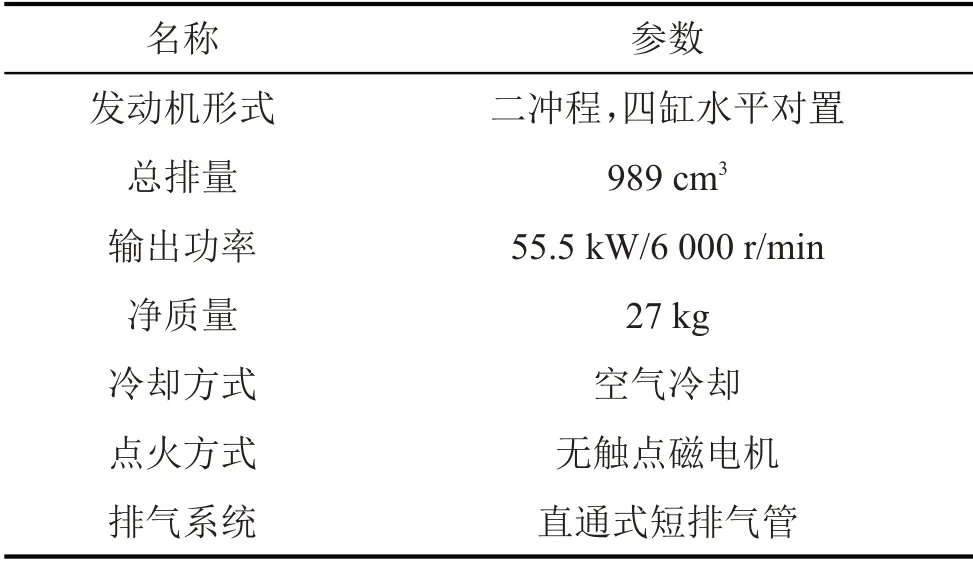
表1 实验发动机主要参数

无人机发动机的声音主要由其发动机本机噪声与螺桨噪声两部分构成：发动机噪声包括燃烧噪声、结构噪声和空气动力性噪声等类型，且以进、排气产生的气动噪声为主。螺桨噪声主要源自发动机工作时桨叶与周围空气周期性作用[6]。通过盲源分离技术将无人机发动机声音信号分离后，可以为进一步的发动机故障定位和诊断提供必要的数据基础。

1.2 实验测试系统

本文针对无人机发动机开车声音信号设计了一个多通道声音信号采集分离系统，该系统主要运行过程是：在某无人机发动机实验室将多个传声器布置在发动机周围，再由数据采集系统将发动机开车声音信号采集后传输到信号分析软件，打包成.mat文件后在计算机中用EMD-NLPCA算法完成信号分离。系统框图如图1所示。

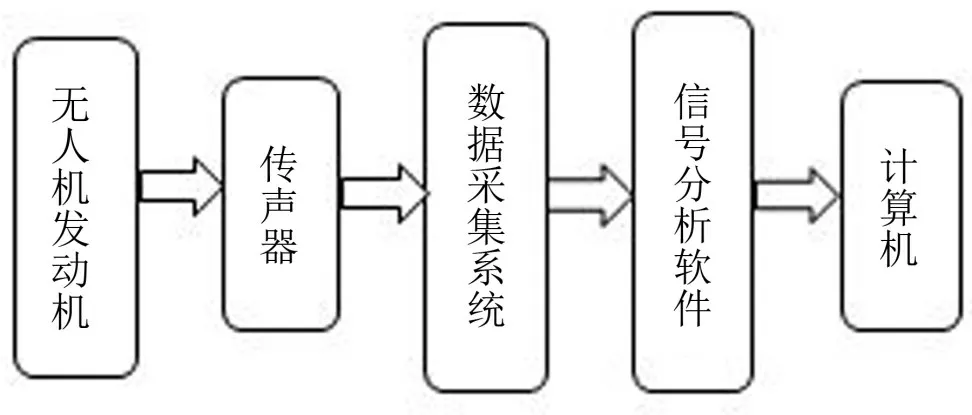
图1 系统框图

（1）数据采集系统

本次实验中采用的数据采集系统为USB4004动态数据采集器，它处理数据精度高且非常容易上手，还具有体积小、重量轻、便于移动的优势，其主要技术指标如表2所示。

表2 主要技术指标

（2）信号采集及处理分析软件

本次实验中使用HSDASP 信号分析系统，其功能特点如表3所示。

表3 主要功能特点

（3）传声器和放大器

实验中采用国营红声的声学传声器和前置放大器，前置放大器由恒流源供电，采用BNC插头输出，具有高输入阻抗、低输出阻抗、低噪声等特点，使用时可很方便与一般的测量仪器连接。

2 实验过程

本次测试在某研究所的发动机试验间进行。该发动机试验间为五面铺有吸声材料的半消声室，地面铺设瓷砖。

2.1 测量点布置

为了保证测试信号彼此的独立性，在用本文算法分离传声器采集到的信号之前，要先检测这些信号之间的差异性。

假设xi（i=1，2，3，…，n）是传声器采集到的信号，n为传声器数目。则传声器采集到的信号之间的相关系数如式（1）所示：

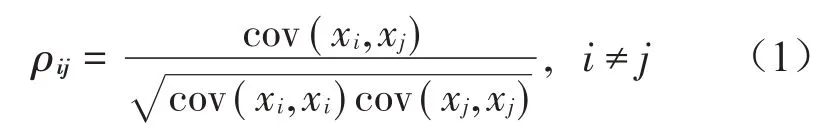
式中：cov（）表示方差。由概率论知识可知，相似系数具有如下性质：|ρij|≤1。

|ρij|=1 表示xi和xj完全相似，即存在关系p(xj=a*xi+b)=1，其中a、b为常数，且a≠0；|ρij|=0，表示xi和xj相互统计独立。

传声器采集到的信号之间的差异性越大，|ρij|越接近于0。

在实验中其实是通过调整传声器测量位置来调节 |ρij|的值，从而保证传声器采集到的信号之间的差异性足以使盲源分离算法达到其应有的效果。反过来说，|ρij|的值也是确定传声器测量位置的标准，在经过反复测试后得出 |ρij|的值至少小于0.5时，传声器采集到的信号之间的差异性才能确保盲源分离的效果。当传声器测量位置确定后，也就必然保证了 |ρij|的值小于0.5，因此不需要每次都求传声器采集信号之间的相关系数。

4 个传声器M1、M2、M3、M4 的测量位置如图2所示，其具体数据见表4，传声器采集到的信号之间的相关系数见表5。

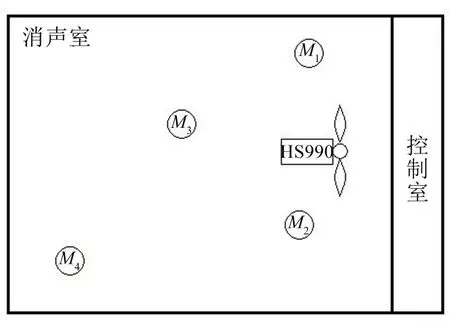
图2 传声器的测量位置概图

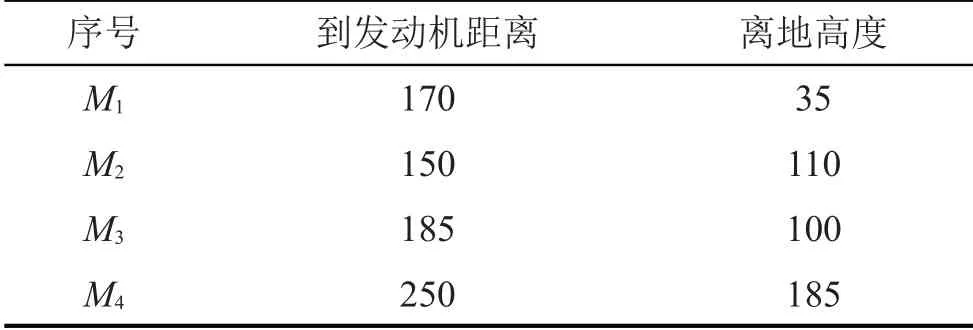
表4 测量位置/cm

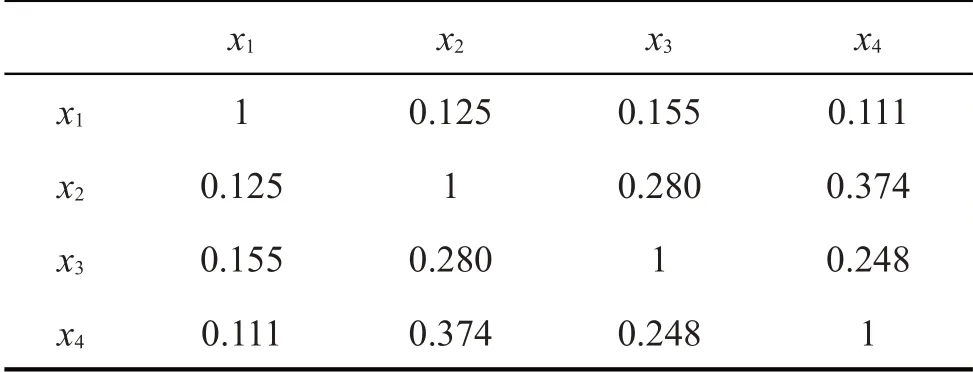
表5 信号相关系数

为了对应欠定情况，在随后的实验中仅随机选取3路信号进行处理。

2.2 实验过程

（1）启动风机，在工况正常后，选靠近风机的位置用传声器采集风机噪声，设置采样频率为32 kHz；

（2）启动发动机，保证工况正常，使发动机实现3 000 r/min稳定运行；

（3）采集传声器信号，采样频率设置为32 kHz；

（4）计算各传声器所采集信号的相关系数，以确保他们的可用性；

（5）利用EMD-NLPCA 算法，对所采集的混合信号进行盲源分离；

2.3 测试结果

（1）采集到的风机噪声

实验时截取16 000 个采样点的信号进行分析，风机噪声的时域图和频域图如图3所示。

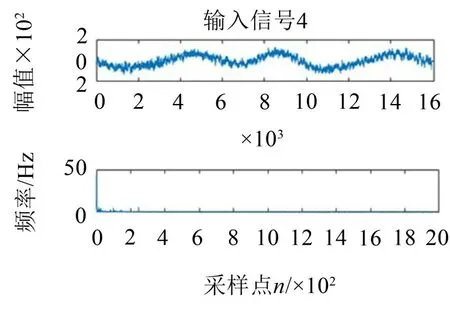
图3 风机噪声的时域图和频域图

（2）3 000 r/min时的发动机开车声音信号

在发动机的测试实验中通常需要先把发动机调到一个较高的转速，因此在本实验中先采集3 000 r/min转速下的信号。

实验时截取16 000 个采样点来做盲源分离，使用4个传声器采集到4个不同位置的声音信号，由于文中的算法可以实现欠定盲源分离，因此只取3 路观测信号，观测信号的时域波形如图4所示。

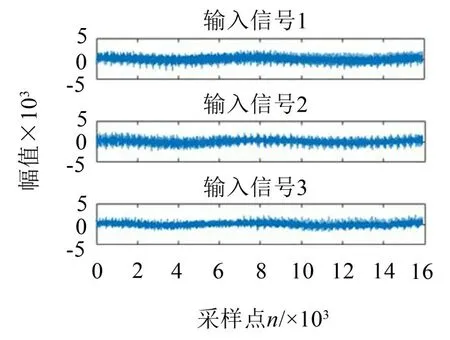
图4 观测信号的时域图

3 EMD-NLPCA盲源分离算法

EMD-NLPCA算法是一种处理欠定情况下非线性混合信号的盲源分离算法。该算法的思路主要是将混合信号进行经验模态分解（Empirical Mode Decomposition，EMD)[7]处理，混合信号被分解成若干个本征模函数（Intrinsic Mode Function，IMF）分量，再将这些IMF分量重构得到新的信号序列。在本实验中，对3路采集信号分别进行EMD处理，得到3个重组信号后将其线性混合成一路新信号，再把这个新信号和原来的混合信号合并，组成新的观测信号组，最终构成正定的盲源分离模型，再用非线性主成分分析[8]盲源分离算法进行分离，最后恢复出源信号。以单通道混合为例，具体步骤如下：

（1）将混合观测信号X(t) 进行零均值和白化预处理。

（2）对预处理后的观测信号X(t)进行EMD 处理，得到n个IMF分量ci(t)，i=1,2，…，n。

（3）将这n个IMF 分量ci(t)进行PCA 降维，得到k个IMF分量ci(t)。

（4）将这k个IMF 分量ci(t)进行一维重构，具体做法是对求出的k个IMF 分量给予（0，1）之间的不同的随机权值并相加，得到新的信号X′(t)，再令h(t)=[X(t);X′(t)]，得到新的观测信号。

（5）利用重构出来的新观测信号作为基于非线性主成分分析的盲源分离算法的观测信号，实现盲源分离,见式（2）：

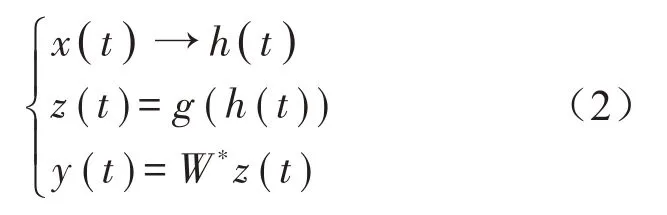
式中：g是进行非线性混合逆变换所构成混合系数为A的线性混合，W=PDA-1（P和D分别为置换矩阵和对角尺度矩阵），则y(t)=P*D*s(t)，即实现了分离，输出y等于各分量经重新排列和尺度缩放后的源信号。

4 分离结果与分析

将图4所示的采集信号作为输入，利用基于EMD-NLPCA的欠定非线性盲源分离算法对混合信号进行分离，并对分离出的信号进行傅里叶变换，得到信号的频谱，图5、图6分别为分离信号的时域图与频域图。

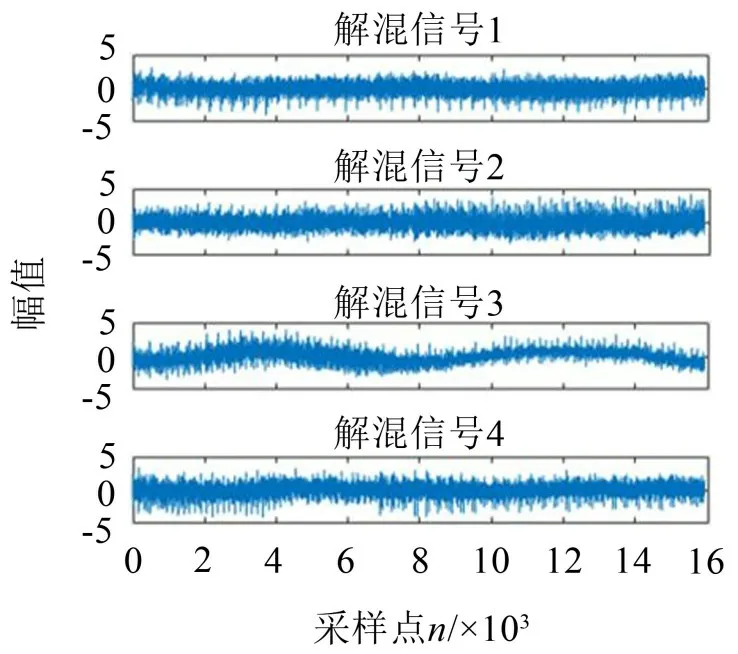
图5 分离信号的时域图

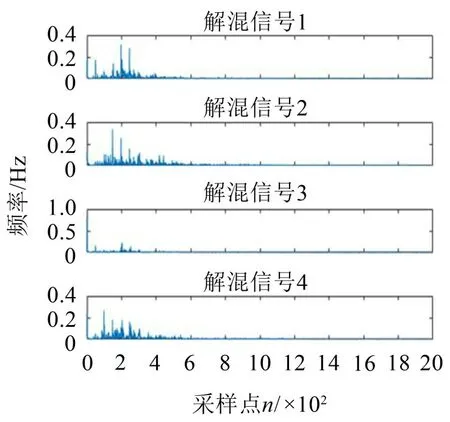
图6 分离信号的频域图

由螺桨噪声的频谱成分为转轴基频、叶片通过频率（Blade Passing Frequency，BPF）基频及其谐波特性，转轴基频的计算公式见式（3）[9]：

式中：f为频率，单位为Hz；n为发动机转速，单位为r/min；而BPF噪声的基频由式（4）计算：

式中：f为频率，单位为Hz；n为发动机转速，单位为r/min，z为叶片数。

一般来讲，发动机排气噪声的频率特性与转速、排量、气缸数等参数密切相关，而且它的频谱呈宽频特性，主要频率成分包括周期性排气噪声、气缸共振噪声以及其他噪声频率。周期性排气噪声频谱中包括汽油机点火频率成分及其高次谐波，其基频可用式（5）计算[10]。

式中：f为频率，单位为Hz；n为发动机转速，单位为r/min，z为气缸数，τ为冲程系数，四冲程汽油机τ=2二冲程汽油机τ=1。气缸共振噪声是由燃烧气体激发气缸内部共振产生的，其基频可用式（6）计算[10]。

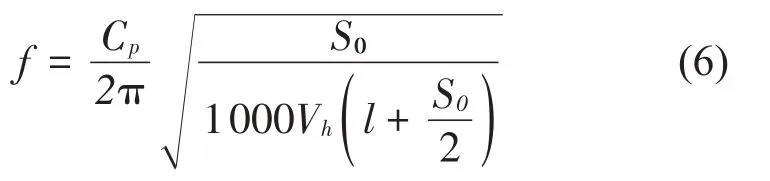
式中：f为频率，单位为Hz；Cp为排气管中声速，单位为cm/s，Vh为总排量，单位为L；l为排气管长度，单位为cm；S为排气口平均面积，单位为cm2。气缸的Helmholtz共振噪声共振频率见式（7）[10]：

式中：S=πr2，气门半径为r，且L＞＞r。该噪声不随发动机转速变化，它源于气缸内的气体共振。

本实验中，发动机转速为3 000 r/min，叶片数为4，则可以算出螺旋桨叶片通过频率的基频为200 Hz，转轴基频为50 Hz。由图6可见解混信号1中幅值较大的频率和螺桨噪声的频谱接近，因此解混信号1对应的源信号可能为发动机螺桨噪声。

发动机气缸数为4，冲程数为2，则可以算出周期性排气噪声基频为200 Hz；发动机排气口直径为0.4 cm，排气管长度为1.5 cm，排量为0.989 L，排气管中声速经推算为681 m/s，则可以算出气缸共振噪声基频为150 Hz，由图6可见解混信号2中幅值较大的频率和排气噪声的频谱接近，因此解混信号2 对应的源信号可能为发动机排气噪声。

对比图6中解混信号3 的频谱特点和风机噪声的频域图，不难看出解混信号3 对应的源信号可能为发动机实验间的风机噪声和其他背景噪声。

通过查阅资料，图6中解混信号4对应的源信号可能为发动机的其他机械噪声。

通过以上分析可以发现采用EMD-NLPCA算法成功地通过3路采集信号分离出了特征独立的发动机螺桨噪声、排气噪声、实验间的风机噪声和其他背景噪声、发动机的其他机械噪声，有效地解决了欠定非线性BSS问题。

5 结语

本文针对无人机发动机开车试验声音信号，设计了一个声音采集系统，选取3路采集信号用EMDNLPCA 算法成功将其分离为4 个具有不同特征的解混信号，有效应对了欠定BSS问题，再通过分析可知解混信号分别为发动机螺桨声、排气声、试验间风机与背景噪声，以及其他机械声。进一步可在此分离数据的基础上开展发动机的故障定位和诊断技术研究，为无人机及其动力系统的健康管理和安全运行提供新的思路和方法。