运营桥梁的变形程度评价和预测分析

2022-08-19郝付军

噪声与振动控制 2022年4期

郝付军

（陕西铁路工程职业技术学院国际交通学院，陕西渭南 714099）

桥梁是公路交通建设过程中的重要构造物，其在运营过程中一旦失稳，会造成不可估量的后果，因此，开展运营桥梁研究具有重要意义[1－3]。目前，已有学者开展了运营桥梁的相关研究，颜飞等[4]利用监测数据进行了仿真分析，以评价桥梁运营质量；阚有俊[5]、董俊等[6]进行了运营桥梁的危险性研究和预警分析，为其安全评价提供了依据。虽取得上述成果，但这些研究中均缺乏桥梁变形程度评价及预测分析，进而仍需对其进一步拓展研究。变形是桥梁安全现状的直观体现，加之变形数据可由现场监测得到，因此，利用现场变形监测成果来开展桥梁变形程度评价和预测分析是可行的，其中，在变形程度评价方面，认为桥梁变形具有极限值，因此，可通过极限位移准则来开展其变形程度评价；在变形预测分析方面，认为监测环境条件会对变形数据造成一定影响，即会使其含有一定的误差信息，影响后续预测效果，因此，在进行变形预测前，有必要进行变形数据的信息分离，且考虑到核极限学习机具有较强的非线性预测能力[7]，误差序列具有较强的混沌特性[8]，因此，可在变形数据信息分离基础上，利用核极限学习机和混沌理论构建桥梁变形预测模型。综合上述，基于桥梁现场变形监测成果，先利用极限位移准则进行桥梁变形程度评价，再在变形数据信息分离基础上，利用核极限学习机和混沌理论实现桥梁变形预测；最后，对比两者分析结果，综合评价桥梁的运营状况。

1 基本原理

结合论文思路，可进一步将分析过程划分为两阶段，即：

阶段一为变形程度评价。利用极限位移准则，求解桥梁变形程度的分级指标，以开展桥梁变形程度评价。

阶段二为变形预测分析。先利用自适应局部均值的经验模态分解实现桥梁变形数据的趋势项和误差项分离，再利用优化核极限学习机实现趋势项预测，并利用混沌理论弱化预测误差，以完成桥梁变形预测。

最后，对比变形程度评价结果和变形预测分析结果，综合判断桥梁运营状况。

1.1 变形程度评价模型的构建

一般认为，桥梁工程在施工完成后，其后期变形具有极限变形值，即当桥梁变形达到一定值后，变形不再继续，因此，现有变形值与极限变形值的差值越大，说明桥梁后期仍具较大变形可能，变形程度相对较低；反之，现有变形值与极限变形值较为接近，则桥梁变形程度较高。前述即为桥梁变形程度评价过程中的极限位移准则，依据其思路，可利用现有变形值和极限变形值构建变形程度分级指标Fr：

式中：Sc为极限变形值；St为现有变形值。

根据式(1)欲求得指标Fr，需得到参数Sc和St，其中，参数St可由现场监测成果统计得到；Sc参数则需通过求解得到。

由文献[9]的研究成果得采用指数模型求解极值效果良好，进而利用其实现极限变形值Sc的求解，即：

式中：Y为拟合变形值；a、b、k为拟合参数；t为时间变量。

因此，以变形监测成果为基础，通过软件可拟合式(2)；且据式(2)函数形式可知，当时间变量t趋于无穷大时，变形值趋近于定值a，且为极大值，因此，以其作为极限变形值Sc是可行的。

据分级指标Fr的含义可知，其值越大，变形程度也相对越大，进而可利用其实现桥梁变形程度的分级，具体标准如表1所示。

表1 桥梁变形程度分级划分标准

1.2 变形预测模型的构建

由于桥梁变形数据具有较强的非线性特征，单一模型难以完全刻画其变形规律，因此，提出基于数据信息分离的优化组合预测思路来开展桥梁变形预测，其预测过程大致被划分为3个环节，即变形信息分离、趋势项预测和误差弱化预测。

1.2.1 变形信息分离模型的构建

受监测环境因素的影响，桥梁变形数据中往往含有一定的误差信息，其对预测结果具有显著影响，因此，开展桥梁变形数据的趋势项和误差项分离显得十分必要。经验模态分解（Empirical Mode Decomposition，EMD）是一种常用的信息分解方法，其在变形数据极值点分布特性识别基础上，可将数据信息分解为若干固态模量，且由于它是按照信号局部时间尺度进行分解，可使得其基函数具有较强的自适应性，已被广泛应用。

值得指出的是，基于EMD模型的信息分解依赖于局部极值点的特征尺度，若变形数据受到信号干扰，将会影响极值点的基本特征，进而造成分解过程不准确；为解决该问题，提出利用自适应局部均值（Adaptive Local Mean，ALM）算法对EMD 模型进行优化处理[10－11]，其优化过程为：先利用积分中值定理求解变形数据中所有极值点的局部特征尺度，再对局部均值进行拟合，并评估不同极值条件下局部均值对频率分量的拟合度，以实现最优极值阶次的自适应求解。因此，确定桥梁变形数据信息分离模型为ALM-EMD模型。

同时，需进一步构建变形数据信息分离的效果评价指标，目前，信噪比是常用的信息分离效果评价指标，但在实际应用过程中，有效信号的功率和噪声信号的功率是未知的，使得以信噪比评价分离效果存在一定的不合理性。为解决该问题，以信噪比指标为基础，构建出降噪误差比dnSNR：

式中：Ps为含误差因素的功率；Pg为滤除误差因素的功率。

其中：，Ps和Pg的计算公式如下：

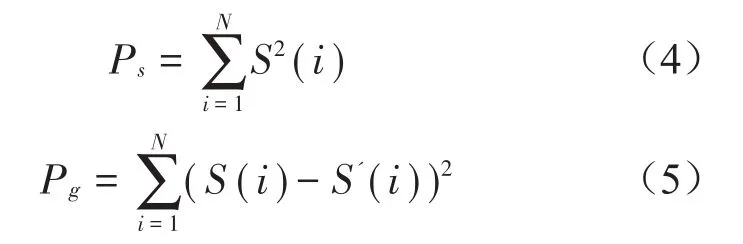
式中：S(i)为原始变形序列；S′(i)为经分解处理后的变形序列。

降噪误差比dnSNR 的评价判据为：dnSNR 值越大，信息分离效果相对越差；反之，信息分离效果相对越好。

1.2.2 趋势项预测模型的构建

核极限学习机（Kernel Extreme Learning Machine，KELM）是一种新型神经网络，相较于传统极限学习机，前者具有更快的收敛速度和泛化能力，适用于非线性预测，但在其应用过程中，也存在一定问题，如激励函数由使用者确定，主观性相对较强，依赖于使用者经验，正则化系数由模型随机确定，其最优性难以保证。

为保证KELM 模型的参数最优性，对上述问题均进行优化处理：

（1）激励函数的优化处理。核极限学习机的常用激励函数有3种，即Sine型、Hardlim型和Sigmiod型，三者的适用性存在一定差异，为达到优化目的，提出对三者的预测效果均进行计算，选取效果最佳者作为KELM模型的激励函数。

（2）正则化系数的优化处理。由于正则化系数具有范围取值特征，不能用上述试算法进行优化处理，且考虑到鸟群算法（Bird Swarm Algorithm，BSA）具有较强的全局寻优能力，故利用其实现KELM 模型的正则化系数优化。BSA 算法是于2016年提出的新型智能优化算法，能通过鸟群间的信息贡献和搜索策略来实现参数寻优，其优化过程可被划分为3个行为：

①觅食行为。通过Logistics 映射将个体鸟映射至D 维空间的初始位置，并根据个体经验和鸟群经验进行觅食行为。

②警戒行为。一般情况下，警觉性高的鸟比警觉性低的鸟具有相对更强的竞争优势，即更易靠近鸟群中心，因此，个体鸟可通过警戒行为来向鸟群中心移动。

③飞行行为。警觉性高的鸟可为生产者寻找食物，而警觉性低的鸟则可变成索取者，向生产者获取食物，因此，索取者可通过飞行行为来追随生产者。

对激励函数和正则化系数的优化处理有效保证了KELM模型的参数最优性；同时，将趋势项的预测误差与前述分解的误差项叠加，组成新的误差序列，以便后续误差弱化处理。

为便于后续描述，将优化激励函数后的模型命名为初步参数优化KELM模型，将再经BSA算法优化的模型命名为BSA-KELM模型。

1.2.3 误差弱化预测模型的构建

误差序列具有较强的随机性，使得其混沌特征显著，因此，提出利用混沌理论实现误差弱化预测。

先利用Lyapunov 指数法进行误差序列的混沌特征判别，即先求解混沌指数λmax，若λmax＜0，说明误差序列无混沌特征；反之，说明误差序列具混沌特性，可利用混沌理论进行误差序列的弱化处理。

其次，将误差序列表示为{εi，i=1,2…n}，并基于时间参数τ和嵌入参数m将误差序列进行相空间重构：

式中：ψi为第i个空间相点矩阵，式(6)中[]为矩阵符号；T为矩阵转置符号。以ψi为预测中心，将其与ψl（最近相邻点）间的距离d表示为：

欲达到误差弱化的目的，d值应保持最小，则误差弱化预测模型可表示为：

式中：λmax为由Lyapunov指数法求得混沌指数。

最后，利用ψi+l反推出εi+1，即可完成误差弱化处理。

将趋势项预测结果和误差项预测结果相加，所得值即为桥梁变形预测值。

2 实例分析

2.1 工程概况

大渡河大桥位于四川省泸定县，属水电交通复建工程，长度为366.57 m，属大跨度预应力混凝土钢结构桥梁，共设计了8个墩柱（由大桥右岸至左岸的墩编号为1#墩～8#墩），引桥采用3 m×13 m和2 m×13 m的连续实心板现浇。其中，5#墩为本桥梁的主墩，位于河流中部，采用钢筋混凝土双肢截面矩形实心墩。

桥梁的主要技术标准：桥梁等级为三级，设计速度为30 km/h，汽车荷载等级为I级。同时，桥址区地震基本烈度为8 度，峰值加速度为0.25 g，反应谱特征周期为0.4 s。

通过勘察资料，将桥址区的地质条件详述如下：

（1）地形地貌。桥址区地貌为侵蚀构造地貌，地面高程间于600 m～2 100 m，高差相对较大，地形起伏明显，使得山峰高耸，河流流速也较快。

（1）池塘养殖模式。全市池塘养殖大多数采用精养模式，鱼塘基础设施建设较完备，养殖产量较高。一般采取专养、套养等集约化养殖方式。

（2）地层岩性。区内第四系地层主要以坡积物和洪积物为主，其中，坡积物主要以块石和碎石为主，粒径多间于35 mm～65 mm，其间以黏土充填为主；洪积物主要以漂石和卵石为主，粒径多间于40 mm～100 mm，其间以砂充填为主。下覆基岩以晋宁期花岗岩为主，具有中粗粒结构，块状构造，节理裂隙较发育。

（3）地质构造。桥址东侧约500 m 处发育有大渡河断裂带，目前虽处稳定状态，但其演化过程较长，引发了较多的次生构造，对桥址围岩完整性具有一定影响。

由于桥梁变形是其安全的直观体现，因此，在桥梁建成以后，对其进行了桥墩变形监测，监测项目为沉降和倾斜，监测频率为1月/次，且监测仪器为全站仪。

桥梁中部主桥墩变形成果较为完备（监测点位于墩中心位置，即5#主墩），从2015年1月至2017年10月共计得到34个周期的监测成果，并据其作图得其变形曲线如图1所示。

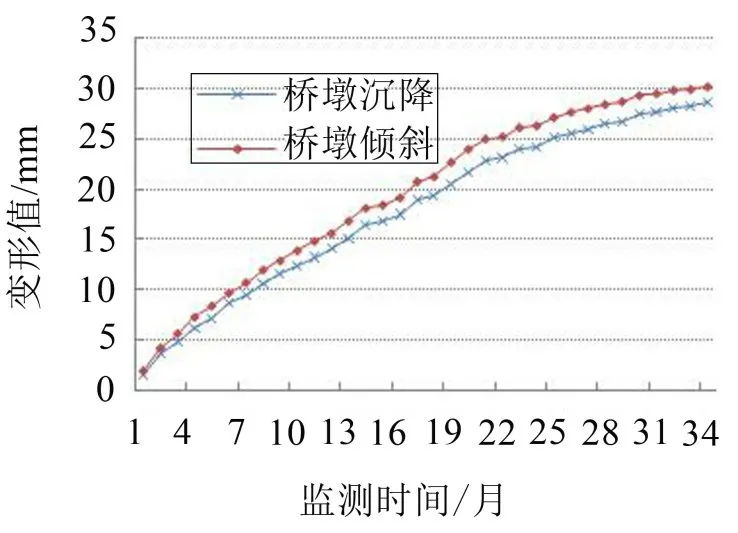
图1 桥梁沉降和倾斜变形曲线

2.2 桥梁变形程度评价

按照变形程度评价思路，通过拟合、计算得到桥梁变形程度分级结果见表2。据表2，在两监测项目的拟合过程中，拟合度均较趋近于1，说明其拟合效果较优，所得极限变形值的可信度较高；结合桥梁的现有变形值，求得桥墩沉降的分级指标值为0.86，桥墩倾斜的分级指标值为0.93，后者的变形程度相对最大，但按照分级标准，两者的变形程度等级均为Ⅳ级，得大渡河桥梁的变形程度已非常高，后期变形将趋于稳定。

表2 桥梁变形程度分级结果

通过桥梁的变形程度评价，得大渡河大桥的桥墩变形程度已相对较大，趋于向稳定方向发展。

2.3 桥梁变形预测分析

2.3.1 变形数据的信息分离处理

在桥梁变形数据信息分解过程中，为充分验证经验模态分解的优越性，将分析过程划分为两部分，其一，在进行EMD 分解的同时，也利用部分小波函数进行信息分解处理，通过对比分析来验证EMD模型的有效性；其二，利用自适应局部均值优化EMD模型，达到变形数据信息分解的优化处理。

表3 不同模型的信息分解结果

其次，再对EMD 模型进行优化处理，得其优化前后的分解结果如图2所示。据图2可知，ALMEMD 模型的dnSNR 值为18.26，小于EMD 模型的19.47，说明通过ALM算法的优化处理，能进一步提升EMD模型的分解能力，验证了优化处理的必要性和有效性。

图2 EMD模型优化前后的分解效果对比

通过上述分析可得EMD 模型相较传统信息分解模型具有显著的优越性，且通过优化处理能进一步提升其分解能力，因此，通过ALM-EMD模型进行桥梁变形数据的信息分离是可行的，即利用其将桥梁变形数据分离为趋势项和误差项。

2.3.2 变形预测分析

在变形预测过程中，为验证该预测模型的滚动预测能力，将预测过程划分为中期预测和后期预测，其中，中期预测是以1～19周期的样本为训练样本，20～24 周期的样本为验证样本；后期预测是以1～29周期的样本为训练样本，30～34周期的样本为验证样本，并外推预测4个周期。

同时，在训练过程中，将输出层设置为预测节点，其对应的输入层是预测节点的前5个变形节点，以此类推。

（1）中期预测结果分析

为验证模型参数的优化处理对趋势项预测结果的影响，以中期桥墩沉降变形为例进行趋势项的优化效果分析；先对3 种激励函数的预测结果进行统计，得表4。

表4 不同激励函数下的预测效果对比

由表4可知，3种激励函数的平均相对误差值具有一定差异，说明三者的预测效果也是不同的，验证了进行激励函数优化筛选的必要性，其中，Sigmiod型激励函数的平均相对误差值为2.94%，相对最小，其次是Sine 型和Hardlim 型，得Sigmiod 型激励函数的预测效果相对最优，将其作为KELM 模型的激励函数。

其次，再利用BSA算法优化KELM模型的正则化系数。为验证BSA算法的优化效果，对BSA算法优化前后的预测结果均进行统计，得表5。据表5可知，在相应验证样本处，BSA-KELM 模型的相对误差均小于初步参数优化KELM 模型的相对误差，且前者的平均相对误差为2.31%，而后者的平均相对误差为2.94%，均是BSA-KELM模型的预测效果相对更好，因此，通过BSA算法的优化处理，能有效提高预测精度，验证了该优化过程的有效性。

据上述趋势项预测结果，可得对KELM 模型的参数进行优化处理虽能有效提高预测精度，但其最终预测结果的平均相对误差为2.31%，预测精度一般，也侧面说明后续进行误差序列弱化处理的必要性。在基于混沌理论的误差弱化预测过程中，采用Lyapunov指数法计算，得λmax为0.762，即误差序列具混沌特性，说明通过混沌理论进行误差序列的弱化预测是合理的，并经统计得到桥梁变形的中期预测结果如表6所示。

表6 桥梁变形的中期预测结果

在桥墩沉降的中期预测结果中，最大、最小相对误差分别为2.02 %和1.83 %，平均相对误差为1.93%；在桥墩倾斜的中期预测结果中，最大、最小相对误差分别为2.07%和1.79%，平均相对误差为1.88%。对比两者预测结果，得两监测项目对于中期预测的预测效果相当，且与表5中的预测结果对比，预测精度得以明显提高，且相对误差均值均小于2%，验证了误差弱化预测的有效性。

表5 BSA算法优化前后的预测结果对比

（2）后期预测结果分析

为验证预测模型的滚动预测能力，再进行桥梁变形的后期预测和外推预测，结果如表7所示。

据表7，两监测项目对于后期预测的平均相对误差介于1.86%～1.87%，两者均较小，且与中期预测效果相当，说明该预测模型不仅具有较高的预测精度，还具有较强的稳定性和滚动预测能力；同时，通过外推预测可得两监测项目的变形值虽会进一步增加，但其增加速率相对较小，趋于向稳定方向发展。

表7 桥梁变形的后期预测结果

2.3.3 预测结果的可靠性验证

为进一步验证该预测模型的有效性，再利用BP神经网络和支持向量机进行桥梁变形预测，以对比验证不同模型的预测效果，结果如表8所示。由表8可知，不同预测模型的预测效果存在一定差异，其中，本文预测模型具有相对最小的平均相对误差和最短的训练时间，其次是支持向量机和BP 神经网络，说明该预测模型相较传统预测模型不仅具有相对更高的预测精度，还具有相对更快的收敛速度，优越性明显。