温度信号检测数据恢复算法研究
2022-08-19蒲琳琳段守富
蒲琳琳,段守富
(1.绵阳职业技术学院电子与信息学院,四川绵阳 621000;2.绵阳师范学院机电工程学院,四川绵阳 621000)
0 引言
在很多测控系统中,温度是一个关键控制参数.热敏电阻测温范围宽,使用方便,广泛应用在各个领域.当环境温度发生改变时,热敏电阻的响应存在滞后,传感器的输出并不能真实反映环境温度的变化,如果信号连续变化,热敏电阻的响应连续滞后,变化频率越高,滞后效应越显著.而航空发动机燃烧室出口温度等都是频率较高的温度信号参数,按照传感器的响应,很容易错过危险的峰值点,从而带来灾难性后果.为此,需要对热敏电阻的检测数据进行恢复处理,通过传感器的读数推算真实的温度变化.
国内外很多学者针对热敏电阻数据还原进行了有益的探索.Atanasijevic[1]等基于负温度系数自热式热敏电阻的热风速计对风机特性进行描述和优化,通过实验研究,重建空气温度.Tan[2]提出了一种低冗余数据采集(LRDC)方案,利用矩阵完成技术降低监测网络的延时和能耗,但是LRDC方案只能选择部分节点来检测数据.Cheng[3]等讨论了如何识别没有领域知识和设置延迟数据的重要性级别,根据重要级别对数据的时间要求,解决能源消耗不平衡的问题.Liu[4]等提出了一种无需系统建模概率分布假设的无源无线声表面波温度传感器系统的算法,并利用附加传感器来获得修正后的电流频率,以修正谐振误差.Dobruck[5]等讨论了作为具有周期性非谐波激励函数的动力系统的变换器电路建模与分析的数学方法,并通过仿真结果验证了理论推导的波形.Pospíšill[6]研究了一类具有任意有限个常时滞的非齐次线性差分方程组,对多个延迟的归纳公式进行了统一,该方法适用于实际计算.Kubanek[7]等提出并分析了实现分数阶带通滤波器响应的两个(α+β)阶传递函数,新系数传递函数的幅频特性与试件函数非常吻合.李文军[8-9]引入时间分数阶微积分,建立了露端式热敏电阻测量接点与被测介质之间的换热过程模型,对传递函数的参数估计也做了探讨.孙斌[10]提出了基于交叉验证的切比雪夫多项式拟合方法的自适应算法,在冷却期间可以精确测定温度传感器在工作现场的动态特性.陈潇[11]等通过实验研究表明温度传感器的热时间常数对校准结果有显著影响.贾培刚[12]等通过Kalman滤波算法对传感器运动误差进行补偿,有效滤除和抑制姿态传感器的运动误差,更好的达到预期效果.薛明喜[13]等研究了自适应Kalman滤波在无源无线SAW测温系统数据纠错中的应用.该算法处理后的温度值与实际温度值的差值,相较处理前明显减小.胡俊峰[14]建立了计入温度效应平台热响应模型,并基于该模型分析平台结构参数与热误差之间的关系.
通过热传导进行检测的所有温度传感器,例如,电阻式温度检测器RTD、热电偶、热敏电阻器以及具有数字和模拟接口的集成IC传感器都有类似特性,具有工程普遍性,因此,对热敏电阻信号处理和恢复进行深入研究具有重要工程实际意义.
1 传统的数据恢复方法及存在的不足
设实际的外部温度为Tin(t),热敏电阻检测到的温度为Tout(t),对应的拉普拉斯变换Tin(s)与Tout(s)满足如下关系:
(1)
假设热敏电阻受到阶跃温度激励,将阶跃前、后的温度分别规范为0、1,设初始温度为T0,阶跃时刻的时间定为t=0,阶跃后温度为T∞,经过时间kT(T为采样周期)后传感器读数为Tk,经过时间(k+1)T后传感器读数为Tk+1,则Tk、Tk+1分别按(2)式规范,由此得到:
(2)
故
(3)
对(3)式进行拉普拉斯反变换得到热敏电阻读数为:
即:
那么,假设从TkT开始计时,并将该时刻定为T0=0,经过时间T后的传感器读数就为T(k+1)T,则(4)式仍然成立,
(4)
将相关参数代入(4)式整理后得到温度恢复公式:
(5)
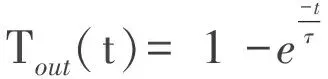
图1的第一条曲线是在附加0.1%~1.0%干扰的情况下得到的仿真结果,从图中看出,干扰很小时,恢复结果良好.
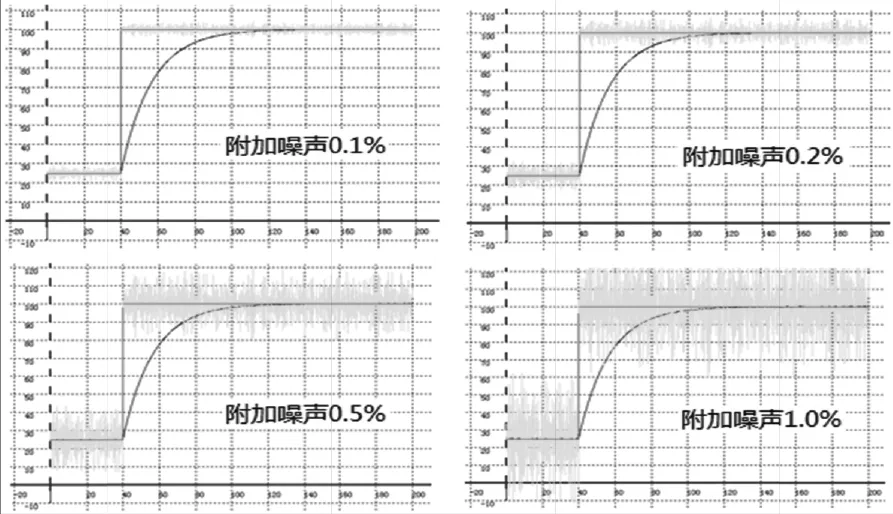
图1 附加四种噪声后的恢复结果Fig.1 Recovery Results after Four Additional Noises
2 低通滤波脉冲传递函数
低通滤波的算法很多,加权算法是其中之一.对前后相邻两次测试结果取如下加权算法:
(6)
式中

连续采样一系列值y1,y2,y3,y4,y5,y6,y7,y8,y9,y10,将测到的值代入(6)式,求得连续的滤波结果:
……
(7)

(8)
当得到第11次检测值y11后,因为a11=0.611=0.003 627 971≈0,从而得到:
(9)
所以,可以利用最近10次的检测值直接得到当前的滤波结果.由此得到递推关系:
(10)
采样开关用于把连续信号变换为脉冲序列.采样过程可用一个周期性闭合的采样开关S来表示.假设采样周期为T,忽略采样持续时间△T,采样器的输入y(t)为连续信号,输出y*(t)可近似为经理想脉冲序列调制后的结果.调制过程在数学上可表示为两者相乘,调制后的采样信号可表示为:
(11)
将式(11)代入式(10)中得:
(12)
对(12)式进行Z变换:
(13)
得到了(13)式的脉冲传递函数后,就可以方便地分析其频率特性,并根据具体的信号特征,按照香浓定理,选取合适的滤波参数a和b了,限于篇幅,这里不做介绍,滤波的效果见图2所示,图中曲线1是在传感器信号中加入20%干扰信号的曲线,曲线2是滤波后的结果,滤波效果理想.

图2 加入20%干扰信号后的滤波仿真结果Fig.2 The Filtering Simulation Results afterthe Addition of the 20% Interference Signal
3 系统模型的优化
综合前面的介绍,加入低通滤波环节后的系统结构图如图3所示.
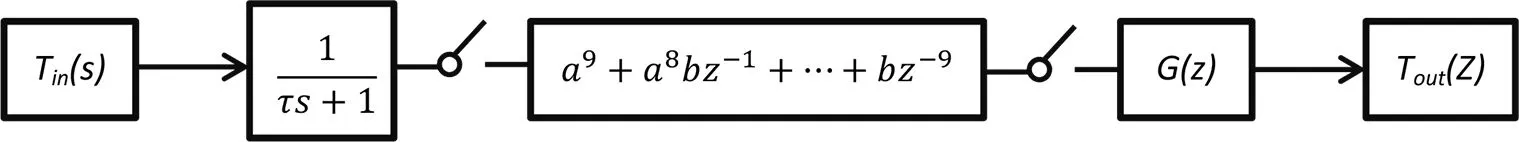
图3 热敏电阻测试和信号处理框图Fig.3 Thermistor Test and Signal Processing Block Diagram
其中,G(z)是数据恢复的脉冲传递函数,对(5)式进行Z变换得到:
(14)

(15)
(16)
(16)式是z的有理分式,按照z变换的特性,
Tout(z)=Tout(0)+Tout(1)z-1+...+Tout(10)z-10+...
(17)
(17)式中,Tout(0)、Tout(1)、……Tout(10)分别对应0、1、10时刻的时域值,可对(16)进行长除得到真实的输入信号如下:
Tin(z)=Tin(0)+Tin(1)z-1+...+Tin(10)z-10+...
(18)
其中,Tin(0)、Tin(1)、……Tin(10)分别对应0、1、10时刻的真实温度值.
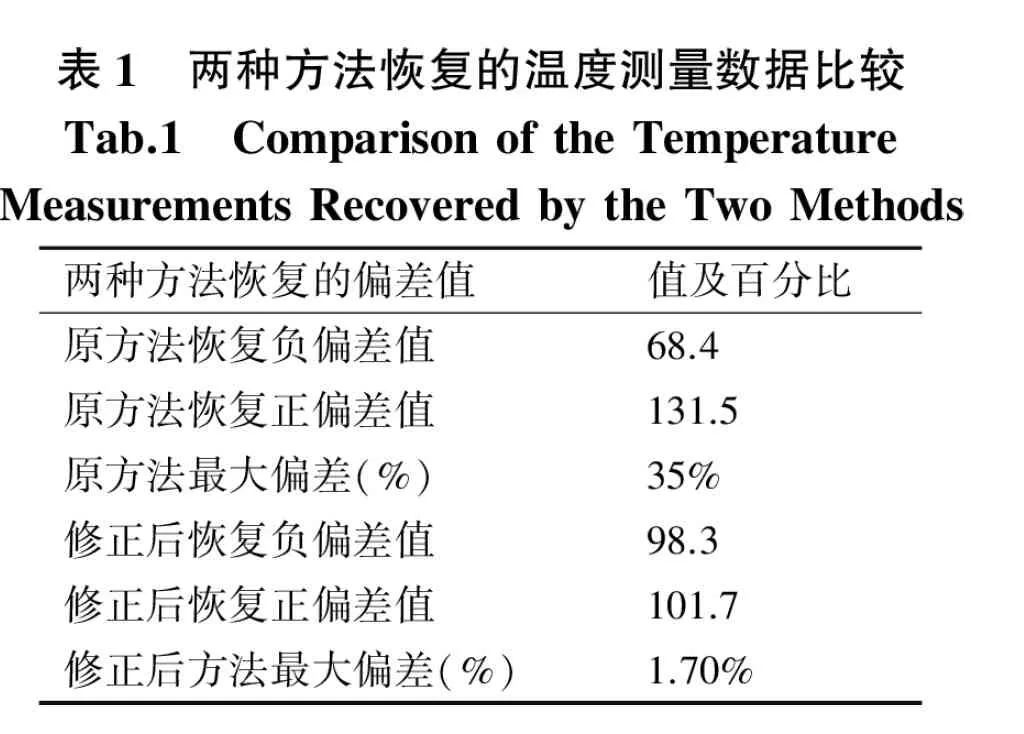
加入低通滤波环节后,对热敏电阻在投入沸水过程中的仿真数据进行处理的结果,如图4所示.线1是恢复后的曲线,仿真数据中加入了20%的白噪声干扰,从图中可以看出,虽然结果还存在一些波动,但已得到了较为理想的处理结果.表1列出了在传感信号中附加20%白噪声干扰后仿真结果的一些统计数据,从表1可以看出,采用低通滤波和Z变换的方法恢复温度数据,增强了抗干扰能力,恢复精度有了显著提高.
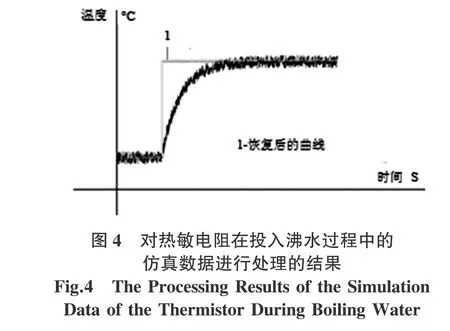
4 结论
(1)加入低通滤波后,根据脉冲传递函数进行温度数据的恢复,增强了抗干扰能力,恢复结果的精度显著提高.
(2)在附加20%干扰信号的情况下,采用原方法,恢复结果偏差超过30%,采用新方法,恢复结果的偏差缩小到1.7%,满足很多工程应用需要.
现场测试数据也表明,真实温度和传感器测试结果偏差很大.数据恢复算法不仅必要,而且可靠.
