浅析积分法求解空间曲面的面积

刘余娇，罗守双

(绵阳师范学院数理学院，四川绵阳 621000)

0 引言

本文从四个方面介绍了空间曲面面积的求解方法：一般曲面面积的求法、曲面参数方程的面积公式、柱面侧面积的求解及定积分求旋转体的侧面积.在绝大多数《高等数学》教材中，只是介绍了一般曲面面积的求法，其他三种方法没有相关介绍，而对大多数非数学专业的理工科学生来说，求解空间曲面面积既是重点也是难点，同时也具有很重要的实际意义.

1 曲面面积的计算方法

1.1 利用定积分求旋转体的侧面积

设平面光滑曲线y=f(x)∈C(a,b),且f(x)≥0,求它绕x轴旋转一周所得到的旋转体的旋转曲面的侧面积.取侧面积元素：位于[x，x+dx]上的圆台的侧面积

积分得到旋转体的侧面积：

(1)

注：侧面积元素dS=2πydS≠2πydx，是因为2πydx不是薄片侧面积的线性主部，从几何意义的角度来说，侧面积元素是位于[x，x+dx]上的圆台侧面积，二不是圆柱侧面积[1].

例1计算圆x2+y2=4在x∈[0,1]⊂[-R,R]上绕x轴旋转一周所得的球台的侧面积S.

例2计算由内摆线x=acos3t,y=asin3t绕x轴旋转一周所得旋转曲面的面积

解利用对称性

1.2 一般曲面面积的求法

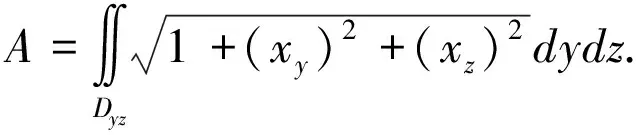
例3求圆柱面x2+y2=2x被球面x2+y2+z2=4截取的面积值[5].

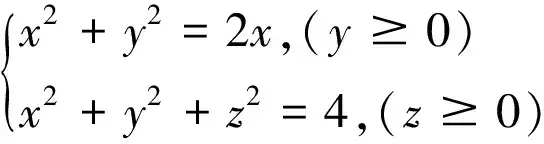
故球面在圆柱面截取的侧面在第一挂限内的面积为

因

则

故所求球面在圆柱面上截取的侧面积为4S=16

1.3 曲面参数方程的面积公式

设曲面∑的参数方程：x=x(u,v)，y=y(u,v),z=z(u,v),(u,v)∈Duv,其中Duv为uv平面上的有界闭区域，若函数x=x(u,v)，y=y(u,v),z=z(u,v)的所有偏导数在Duv上连续，则曲面∑的面积为：

(3)

这里E=xu2+yu2+zu2,G=xv2+yv2+zv2,F=xu·xv+yu·yv+zu·zv.[6]

证明在曲面S中，若

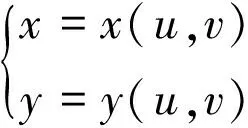
z=z(u(x,y),v(x,y))

(4)

(5)

将(4)(5)代入zx=zu·ux+zvvx,zy=zu·uy+zvvy并计算公式中的被积函数如下：

1+(zx)2+(zy)2=1+(zu·ux+zvvx)2+(zu·uy+zvvy)2

=1+zu2(ux2+uy2)+zv2(vx2+vy2)+2zuzv·(uxvx+uyvy)

将上式展开并配方得

-(xu·xv+yu·yv+zu·zv)]

故公式(2)可化为

记E=xu2+yu2+zu2,G=xv2+yv2+zv2,F=xu·xv+yu·yv+zu·zv，故(3)式得证.

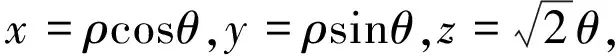
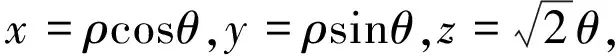
故所求面积为：

1.4 柱面侧面积的求解

在求解柱面的侧面积时，因柱面的侧面垂直于坐标平面，若采用一般曲面的计算方法，往往计算比较复杂，故通常利用第一曲线积分的几何意义求解.

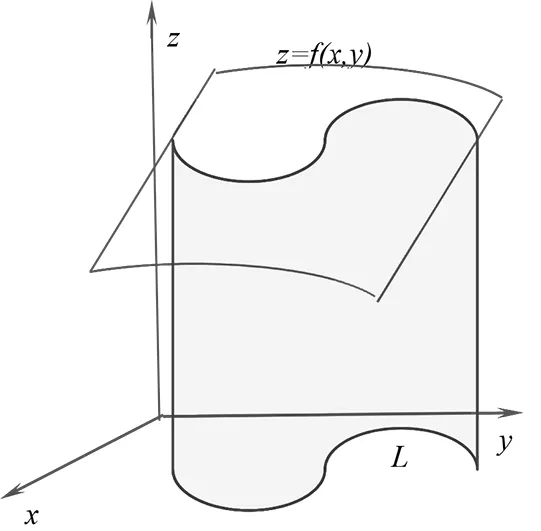
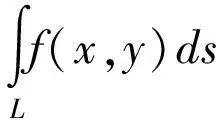
例5(如上例1)求圆柱面x2+y2=2x被球面x2+y2+z2=4截取的面积值[10].

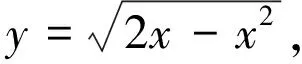
由第一曲线积分的几何意义可知，圆柱面x2+y2=2x被球面x2+y2+z2=4截取在第一象限的面积，即为圆柱面x2+y2=2x夹在球面x2+y2+z2=4，(z≥0)与xoy之间的部分，也即球面在x2+y2+z2=4，(z≥0)在平面xoy上的曲线l:x2+y2=2x上的积分，故所求面积为：

2 结论

本文侧重于利用积分方法对空间曲面面积主要的计算方法的归类与阐述，也是对高等数学教学中关于侧面积求解的补充与扩展.在实际的应用问题中，曲线或曲面方程的形式的多样化，曲面类型的多样化，求解曲面面积的方法也不一样：一般曲面方程采用直角坐标方程表示简单，计算时采用一般求面积的方法，而有的曲面方程采用参数方程简单，或者只能采用参数方程表示，则只能采用参数方程的公式求面积；若所求曲面的类型为柱面的一部分，通常采用第一曲线积分的几何意义求解，计算较为简单，而对旋转曲面的面积计算，采用定积分的方法进行求解.