对一道源自课本的高考试题的再探究
2022-08-19周长春
中学数学杂志 2022年8期
周长春
(北京市第二中学 100010)
2016年浙江省高考数学理科卷第15题为:已知向量,,||=1,||=2,若对任意单位向量,均有则·的最大值是.
文[1]对该题进行了深入的探究,不仅给出了5种不同的解法,而且得到了3个一般化的结论,读后让人深受启发.笔者对该题“再”探究,思考如下问题:
①该题还有没有别的解法?
②如果将改为|·|(其他条件不变),又该如何求解?即如何求(|·|+|·|)?③将②推广到一般情形后的结论又是怎样的?
笔者通过挖掘|·|+|·|的几何意义,借助几何直观,得到如下解决过程.1 利用几何意义求解
(1)构造|·|+|·|的几何意义设与的夹角为θ
,,与的夹角分别为θ
,θ
,则·=2cosθ
,因为求的是·的最大值,故只考虑又因为当θ
=0时,取与,同向,则故只考虑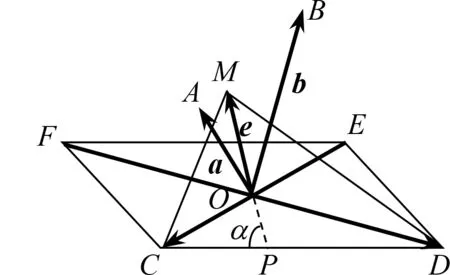
图1
如图1,过点O
作将绕点O
逆时针旋转90°,绕点O
顺时针旋转90°,分别得到向量分别作点C
,D
关于点O
的对称点E
,F
,则四边形CDEF
为平行四边形.当在∠EOF
内(含边界)时,延长MO
交CD
于点P
,记∠OPC
=α
,故|·|+|·|=这就是|·|+|·|的几何意义.(2)求|·|+|·|的最大值下面利用|·|+|·|的几何意义求 |·|+|·|的最大值.当在∠EOF
内(含边界)时,当时取“=”,事实上,此时与+共线.当在∠COD
内(含边界)时,由对称性知当在∠COF
或∠EOD
内时,同理知易知△AOB
≌△EOD
,所以所以在△AOB
与△COD
中,由知故此时综上,因此原题题意等价于即·的最大值是.下面考虑和的情形.
易知
当时,

图2
当时,如图所以(|·|+|·|)事 实上,此时与-共线).由以上分析可知,对任意给定的θ
∈(0,π),=max{|+|,|-|}.当θ
=0或θ
=π时,上述结论也成立.因此,将问题一般化,利用|·|+|·|的几何意义可得出如下结论:设,为非零向量,则对任意单位向量,有(|·|+|·|)=max{|+|,|-|}.设,为非零向量,||=m
,||=n
,利用上面的方法很容易得到文[1]的3个结论,这里就不赘述了.2 几何意义的应用
(1)变式探究
(变式)已知向量,,||=1,||=2,若对任意单位向量,均有则·的最大值是.对任意单位向量,均有因此需要求(|·|+|·|).若
θ
∈(0,π),如图1,当在∠EOF
内(含边界)时,因为所以∠ODC
<∠OCD
,sin∠ODC
P
与点D
重合,即与同向时(此时当在∠COD
内(含边界)时,由对称性知(|·|+|·|)=sinθ.
当在∠COF
或∠EOD
内时,同理知故当⊥时,(|·|+|·|)=sinθ.
若θ
=0或π,则当⊥时,(|·|+|·|)=0=sinθ.
综上,(|·|+|·|)=sinθ.
对于上面的变式,因此即·的最大值是此题如果不采取上述方法,解决起来往往非常麻烦,有兴趣的读者不妨一试.
(2)推广探究
将上述变式推广到一般情形,笔者经过探索得到了如下一系列结论:
结论1
已知非零向量,,||=m
,||=n
(m
≤n
),与的夹角为θ
,为任意单位向量,则当且仅当⊥时,(|·|+|·|)=m
sinθ.
结论2
已知非零向量,,||=m
,||=n
(m
≤n
),若对任意单位向量,均有|·|+ |·|≥r
,其中r
为正常数,则当且仅当r
≤m
时,,存在.结论3
已知非零向量,,||=m
,||=n
(m
≤n
),若对任意单位向量,均有|·|+ |·|≥m
,则⊥.
结论4
已知非零向量,,||=m
,||=n
(m
≤n
),若对任意单位向量,均有|·|+ |·|≥r
,其中常数r
∈(0,m
),则·的取值范围为这些结论的证明方法与上述变式求解过程完全相同,这里略去.
本文是对一道源自课本的高考试题的“再”探究.在探究过程中,一方面强调换个角度思考,深入挖掘|·|+|·|的几何意义,借助几何直观、数形结合来解决问题;另一方面强调变式,并试着做一般化处理.在平时教学中,教师如果能在引导学生多角度思考问题(一题多解)以及对题目进行变式求解(一题多变)方面多花功夫,对于提升学生的数学核心素养、培养学生灵活运用所学知识分析问题和解决问题的能力,是大有裨益的.