新能源汽车PMSM位置传感器故障诊断技术
2022-08-19姚建平代明远
姚建平,代明远
(重庆市科能高级技工学校,重庆 400037)
新能源汽车能够使用新能源代替传统的石化燃料,具有清洁、环保、无噪声、发动机燃烧效率高等优点。由于效率高、噪音小等优点,永磁同步电机(Permanent-Magnet Synchronous Motor,PMSM)逐渐成为主流的新能源汽车驱动系统。永磁同步电机的驱动十分依赖位置传感器测定的转子的准确位置,因此永磁同步电机位置传感器的故障诊断问题深受重视。基于霍尔传感器搭建PMSM矢量控制系统对转子位置进行测量,利用傅里叶分解法得到霍尔信号中包含的谐波类型和振幅,利用基于巴特沃斯原理的低通滤波器和一种基于扩展卡尔曼(Kalman)滤波器的滤波算法对电机信号进行滤波和降噪处理。研究结果表明,基于霍尔传感器搭建的PMSM矢量控制系统能够精确诊断出位置传感器的故障。
1 PMSM矢量控制系统的搭建及优化
1.1 PMSM矢量控制系统下的霍尔故障诊断
自第一辆汽车问世以后,汽车行业迅速发展,如今已成为必不可少的交通代步工具,方便居民的出行,但随之而来的汽车尾气污染环境的问题始终困扰着各国,难以解决。我国是使用汽车数量最多的国家之一,自2010年以后,每年的汽车销量都超过千万。近年来我国汽车的产量和销量如图1所示。
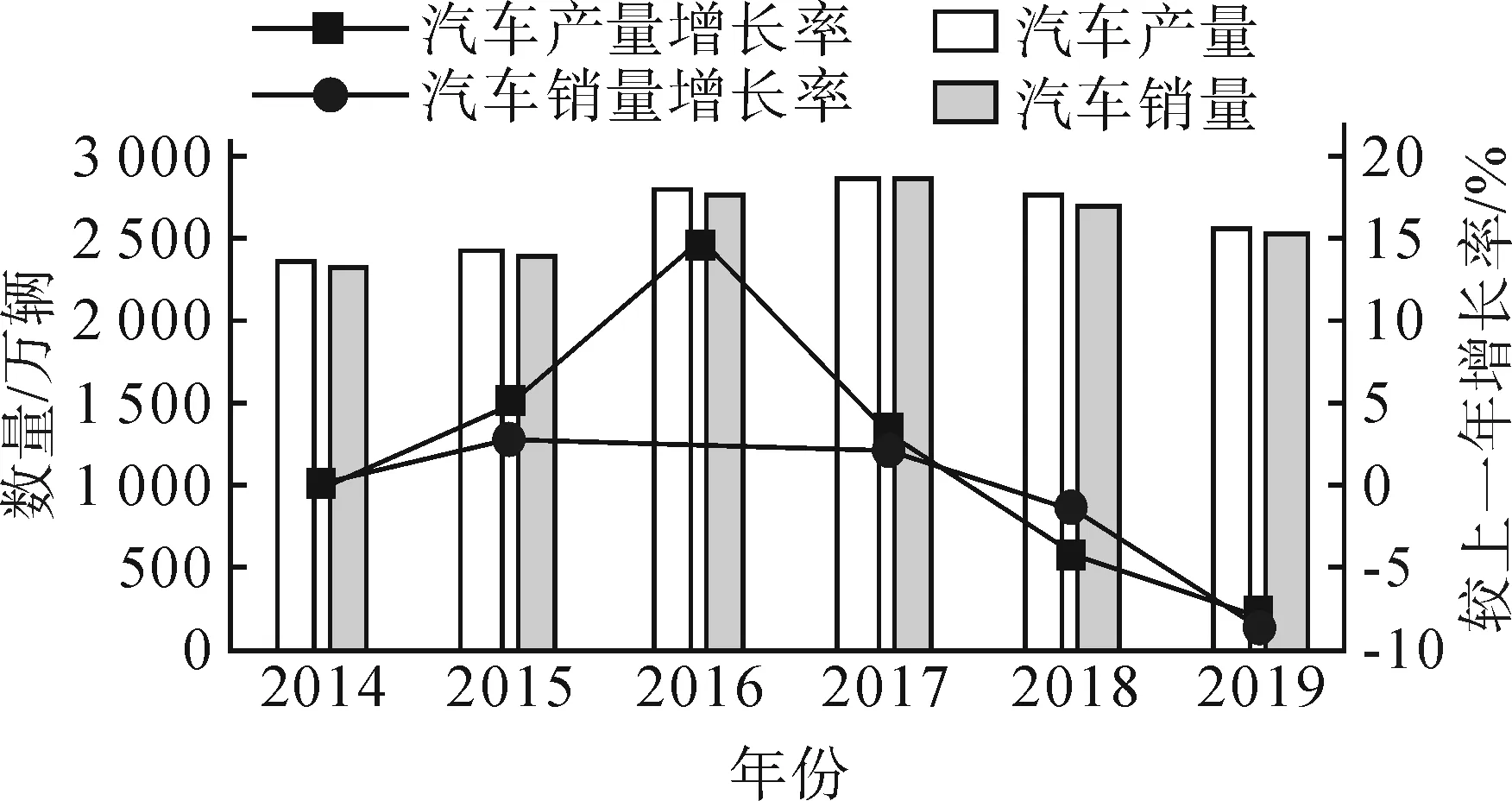
图1 近年我国汽车的产量和销量Fig.1 Output and sales of automobiles in China in recent years
以清洁、环保的新能源为燃料代替传统化石燃料的新能源汽车能够有效解决汽车尾气的污染问题,因而备受各界人士关注和重视。新能源汽车的驱动系统目前主要采用永磁同步电机。为了保证驱动系统的控制精度和响应速度,采用基于霍尔传感器的矢量控制作为控制策略,搭建PMSM矢量控制系统。在PMSM矢量控制系统中,电磁转矩:
=
(1)
式中:表示电磁转矩;表示励磁磁链;表示电流矢量在轴方向上的分量。
电磁转矩的大小取决于永磁同步的电机转速大小,PMSM矢量控制系统中,可以通过调节控制电磁转矩,来解决转子在新能源汽车突然变速时测量位置滞后的问题。
位置传感器是否出现故障决定着PMSM矢量控制系统能否正常运行,因此,位置传感器的性能非常重要。霍尔传感器相对其他位置传感器而言,有着相对较高的环境适应性,但因为天气、道路环境、突发情况、车身震动以及霍尔传感器的使用时长等因素,都会使霍尔传感器的性能变低,出现故障的概率增加。未发生故障的霍尔传感器有3个霍尔元件,即霍尔元件A、霍尔元件B、霍尔元件C。单霍尔故障是指A、B、C这3个霍尔元件中的某一个霍尔元件发生故障,不能继续工作,且输出状态保持高电平或低电平一种状态,不再按规律输出1或0,使霍尔传感器中会出现6种不同的单霍尔状态。这6种状态会使原本确定的6个位置变成4个确定位置,使原本电周期区间的6个区域变成4个区域,其中2个区域为60°扇形;另外2个区域为120°扇形。故障类型可根据故障后的特殊输出信号,如(111)这种零矢量来判定。
双霍尔故障则是3个元件中的某2个元件发生了故障,不能继续工作,且输出状态保持高电平或低电平一种状态,不再按规律输出1或0,使霍尔传感器中会出现12种不同的单霍尔状态,只有一个元件正常工作,提供正确的位置信息。在发生双霍尔故障后,会由正常状态下的6个确定位置变成2个确定位置,相对单霍尔故障的4个进一步减少,且会同时出现“111”以及“000”2种特殊信号,即2种零矢量。此时的电周期区间只有2个区域,分别为180°,并不断变化,霍尔传感器的精度极低。根据上述内容,PMSM矢量控制系统对霍尔传感器故障的检测流程如图2所示。

图2 PMSM控制系统的霍尔故障检测流程Fig.2 Hall fault detection process of PMSM control system
通过霍尔传感器传输的霍尔信号,PMSM矢量控制系统即可根据霍尔信号中包含的信息对霍尔故障类型做出判定,方便维修人员对其进行相应的处理。
1.2 故障状态下霍尔信号的降噪滤波处理
3个元件转动时,根据磁场的变化而按规律输出高电平1和低电平0,根据组合的不同会提供6个确定的位置。6个位置使电周期呈6个彼此相差60°的扇形,由此控制逆变器开关,进而控制永磁同步电机的相电压。正常状态下的霍尔传感器能够提供6个确定的位置,这6个位置使电周期呈6个彼此相差60°的扇形,并对电机转子的位置信息进行反馈。由于传感器本身精度的限制,以及噪声的干扰,会使得霍尔信号受到干扰,对转子实际位置的测量精度降低。霍尔信号中同时包含着基波和数量庞大的高次谐波,这些谐波是在对转子的位置测量过程中,系统本身产生和外界传入的噪声干扰产生的;而霍尔转子的实际位置信息仅存于信号基波内,这些高次谐波会影响霍尔传感器对霍尔转子位置信息获取的的精度,进而影响到系统对永磁同步电机的控制精度。霍尔矢量原本图像会由原本的正弦、余弦形式会因为谐波的影响而变成方波形式,具体如图3所示。

图3 霍尔矢量变化Fig.3 Hall vector change
由于霍尔信号是周期信号,而傅里叶级数可以用正弦函数和余弦函数构成的无穷级数来表示任何周期函数,因此采用傅里叶分解法得到霍尔故障后霍尔信号中的谐波类型和振幅大小。傅里叶级数在定义有界函数时能够展开级数,具体如式(2)所示。

(=0,1,2…)

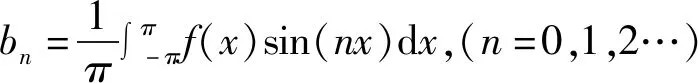
(2)
式中:f(x)为霍尔传感器转子的跳变函数h和h;二者皆可用傅里叶级数展开,如式(3)所示。

(3)
式中:h和h分别是霍尔矢量对转子相角的余弦值和正弦值,且关系如式(4)所示。

(4)
式中:h、h和h表示3个霍尔元件输出状态值变换后获取的新霍尔状态值,这个新状态值与霍尔信号一致,即霍尔信号输出高电平,这3个值输出为1;反之输出为-1。利用基于巴特沃斯原理的低通滤波器依据截止频率对不同频率的谐波进行滤波处理,如式(5)所示。

(5)
式中:ω表示截止频率。霍尔元件故障会引发转速产生波动,进而导致电机振动而而引起噪声污染霍尔信号,此外低通滤波器的滤波处理本身就会引入一些噪声信号,因此需要基于滤波算法对霍尔信号进行降噪处理,以维持其清晰度。针对控制系统,算法对其状态进行测量,具体如式(6)所示。
Z=HX+V
(6)
式中:X为系统的状态方程;V表示测量的噪声。采用3种方式去获取同一个目标值,这个值的大小不一定相等,从而对其进行校正和预测。根据上一次的预测值和测量值得到最优值,并通过状态方程预测下一个值。预测得到状态矢量后,对其进行修正,得到优化后的状态矢量,并根据其计算当前最优估计值的误差,具体如式(7)所示。
P=[1-KC]P
(7)
式中:P为状态估计均方误差;P为状态预测均方误差;K为增益矩阵矢量。
2 PMSM矢量控制系统的性能分析
2.1 PMSM矢量控制系统的故障诊断性能
为了验证基于霍尔传感器的矢量控制系统的诊断正确率,利用软件搭建基于霍尔传感器的矢量控制系统(系统1)和传统的神经网络控制系统(系统2),并进行仿真分析。2个系统的仿真分析结果如表1所示。
从表1可以看出,基于霍尔传感器的矢量控制系统对于单霍尔故障和无故障的诊断正确率为100,对于双霍尔故障和三霍尔故障诊断率有些微误差,分别误判1个,共误判2个,总体误差率为167;而神经网络控制系统对于无故障、单霍尔故障、双霍尔故障、三霍尔故障均有不同程度的误差,分别误判2、4、3和1个,共误判10个,整体误差率为833。基于霍尔传感器的矢量控制系统的误差率比神经网络控制系统要低666。以上结果说明,基于霍尔传感器的矢量控制系统能够精确地诊断永磁同步电机位置传感器的故障,并能精准判断其故障类型。

表1 2种系统的诊断性能对比Tab.1 Comparison of diagnostic performance of two systems
2.2 Kalman滤波算法的降噪效果分析
为了对基于扩展Kalman滤波器的滤波算法的降噪效果进行分析,利用MATLAB软件搭建基于霍尔传感器的PMSM矢量控制系统进行仿真分析,设置总时间长度为50 s,对比经卡尔曼滤波算法降噪后的霍尔信号输出值、降噪前的霍尔信号输出值以及真实值,对比结果如图4所示。
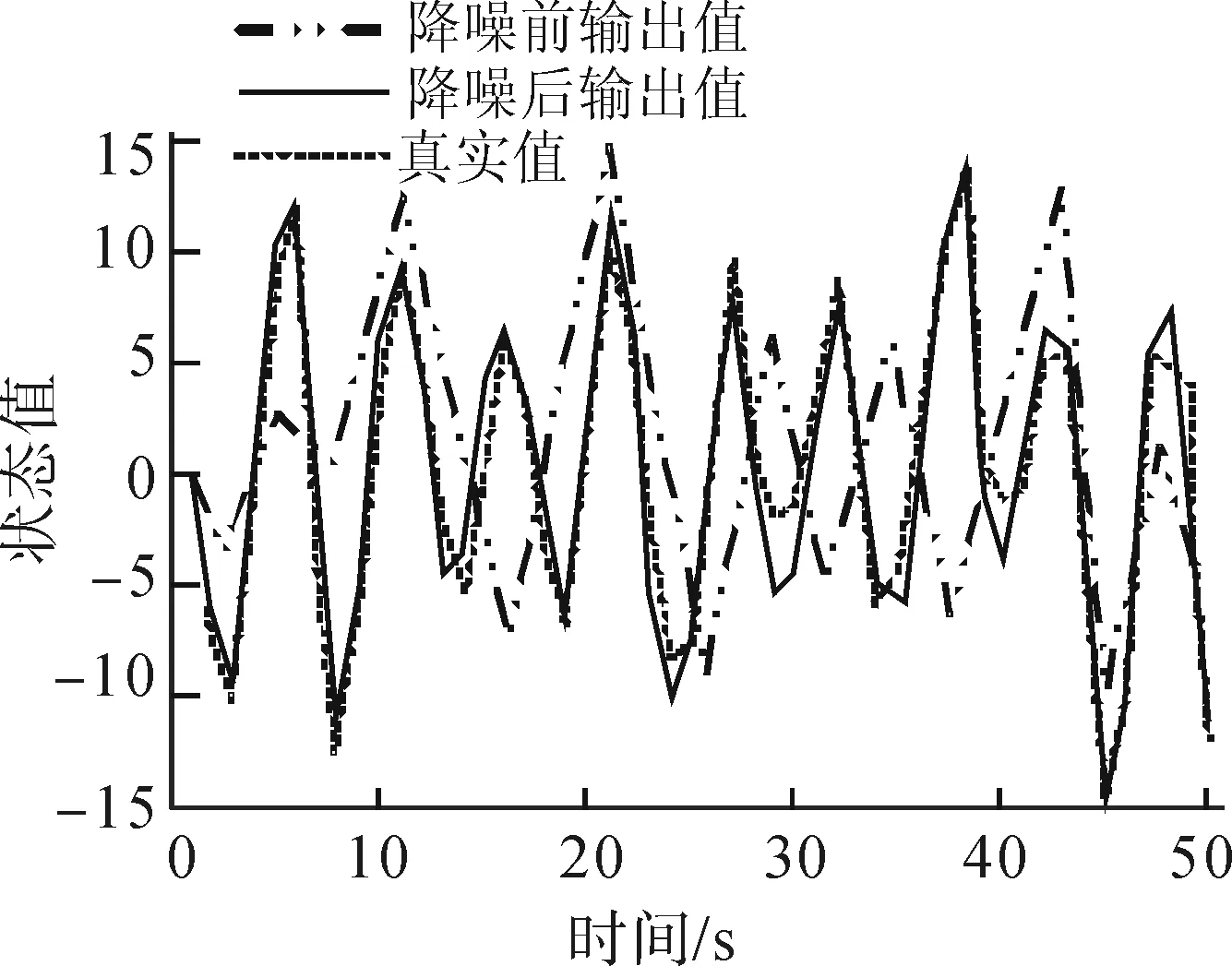
(a)真实值与输出值对比
从图4(a)可以看出,经卡尔曼滤波算法降噪后,PMSM矢量控制系统的霍尔信号输出值与真实霍尔信号值的图像相差不大,几乎重叠;而未降噪的霍尔信号输出值图像跟真实值的图像有着较大的偏差。说明降噪后,系统的霍尔信号输出值非常接近真实值;而降噪前系统的霍尔信号输出值与真实的霍尔信号值有着较大的偏差。
从图4(b)可以看出,在50 s内,经卡尔曼滤波算法降噪后的图像与x轴的面积明显要小于降噪前的图像,说明在50 s内经卡尔曼滤波算法降噪后的霍尔信号输出值的总体误差要远小于降噪前。此外,经卡尔曼滤波算法降噪后系统的霍尔信号输出值最大误差为6,最小误差为0;而降噪前系统的输出值最大误差为8.3,最小误差为0.5。
综上所述,基于扩展Kalman滤波器的滤波算法能够很好的对霍尔信号进行降噪处理,减小PMSM矢量控制系统的霍尔信号输出值误差,使系统能够更精确地诊断位置传感器的故障。
2.3 巴特沃斯原理的低通滤波器滤波效果
霍尔信号中包含的高次谐波会影响霍尔传感器对霍尔转子位置信息获取的的精度,研究采用基于巴特沃斯原理的低通滤波器进行滤波处理,以降低高次谐波对霍尔信号清晰度的影响。搭建PMSM控制系统进行仿真分析,经滤波处理后的频谱与滤波处理前频谱如表2所示。
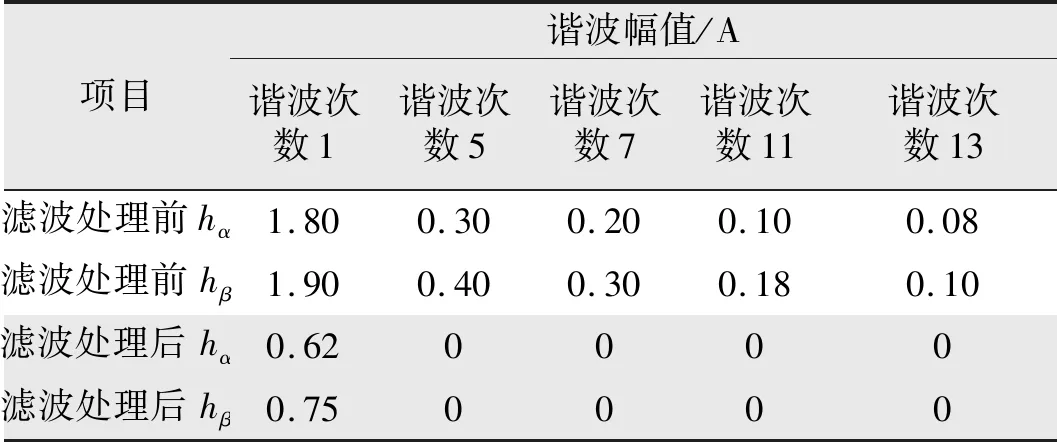
表2 基于巴特沃斯原理的低通滤波器的滤波效果分析Tab.2 Filtering effect analysis of low pass filter based on Butterworth principle
从表2可以看出,在经过基于巴特沃斯原理的低通滤波器的滤波处理前,霍尔信号 和 中除了1次基波以外,信号中还存在大量的5、7、11和13次等高次谐波,且随着谐波的次数越来越高,振幅值越来越小;而在经过基于巴特沃斯原理的低通滤波器的滤波处理后,霍尔信号 和 中的高次谐波均被过滤分离,霍尔信号中仅留下了1次基波。说明巴特沃斯低通滤波器滤波效果良好,能够较好地分离霍尔信号中包含的无用高次谐波,保留存有转子实际位置信息的基波,使系统能够根据霍尔传感器的反馈掌控转子的实际位置。
3 结语
永磁同步电机的驱动十分依赖位置传感器测定的转子的准确位置,因此永磁同步电机位置传感器的故障诊断十分重要。研究基于霍尔传感器搭建PMSM矢量控制系统对转子位置进行测量,利用基于巴特沃斯原理的低通滤波器和一种基于扩展卡尔曼滤波器的滤波算法对电机信号进行滤波和降噪处理。研究结果表明,PMSM矢量控制系统诊断误差率为1.67%,比神经网络控制系统低6.66%;经滤波处理后,霍尔信号中仅留下了基波,说明低通滤波器滤波效果优秀;经卡尔曼滤波算法降噪后系统的霍尔信号输出值最大误差为6,最小误差为0,且误差值远小于降噪前,说明卡尔曼滤波算法能够有效降噪,提高系统性能。以上结果说明,PMSM矢量控制系统能够精确地诊断PMSM位置传感器的故障和故障类型,有实用价值;但研究未针对系统在各种情况下的稳定性进行探讨,还需要后续进一步研究。
