混氢天然气管道标准孔板流量计适应性研究
2022-08-18王国云李长俊贾文龙
王国云 李长俊,2 贾文龙,2
1.西南石油大学石油与天然气工程学院 2.西南石油大学油气储运专业CNPC重点实验室
氢能是一种绿色、低污染、可再生的燃料,被认为是最有前途的化石燃料替代品之一[1]。目前,利用可再生能源电解制氢,然后将氢气按照一定比例掺入天然气管道中进行输送是利用和运输氢能的有效途径[2-5]。如IEA GHG R&D项目掺入天然气管网中的氢气摩尔分数高达25%[6];A Meland项目掺入天然气管网中的氢气摩尔分数达到20%[7-8]。而掺氢天然气计量技术是掺氢天然气产规模化和市场化的重要基础[9-10]。标准孔板流量计由于其设计简单、成本低、可靠性高,仍然是石油与天然气行业中使用最广泛的流量计[11]。
由于氢气和甲烷物性差异巨大,在标况下其密度相差8倍以上[12],而密度是影响标准孔板流量计结果的重要因素[13]。当天然气中掺混氢气后,会导致其密度、黏度、比热容参数改变,进而影响标准孔板流量计计量准确度。Dong等[14]利用Fluent分析不同倾角孔板在测量天然气流量时对测量准确度的影响;Jin等[15]利用Fluent分析得到在测量液氢时不同孔板结构对流出系数和压力损失系数的影响;李思达[16]通过数值模拟技术得到在测量天然气流量时,流体相对密度变化值对测量值有较大的影响。
尽管前人已经做了很多研究,但目前对影响测量准确度的研究主要集中在孔板结构的变化上,这将会增加流量计结构的复杂性,而且在实际的天然气管道中不易使用。此外,所研究的结论主要是对流出系数、差压等的影响,关于其他计量所需参数,如可膨胀系数、超压缩系数、相对密度系数的影响很少被研究。研究的介质主要是天然气或者液氢,关于混氢天然气的情况很少被研究。因此,本研究主要分析天然气管道中混入氢气后对标准孔板流量计测量准确度的影响。
1 标准孔板流量计工作原理
标准孔板流量计以能量守恒定律和流动连续性方程为基础,通过测量孔板前后产生的静压力差来衡量天然气流过节流装置的流量大小[17]。工况条件下的体积流量一般用流量计测量,然后换算成基本(标准)条件下的体积作为天然气贸易交接过程中的流量[18]。GB/T 21446-2008《用标准孔板流量计测量天然气流量》以293.15 K、101.325 kPa为条件,得到标准条件下天然气体积流量计算实用公式,如式(1)所示[19-20]:
(1)
式中:qVn为标准条件下天然气体积流量,m3/s;AVn为体积流量系数,AVn=3.179 5×10-6;C为流出系数;E为渐进速度系数,E=1/(1-β4)0.5;β为孔径比,β=d/D;d为孔板开孔直径,mm;D为测量管内径,mm;FG为相对密度系数;ε为可膨胀系数;FZ为超压缩系数;FT为流动温度系数;p1为孔板上游取压孔实测绝对压力,MPa;Δp为孔板前后差压,MPa。
流出系数C的计算公式如式(2)~式(4)所示。
C=0.596 1+0.026 1β2-0.216β8+
(2)
(3)
(4)
式中:ReD管径为雷诺数;L1为孔板上游端面到取压孔轴线的距离除以测量管内径得出的商;L2为孔板下游端面到取压孔轴线的距离除以测量管内径得出的商;M2为变量;A为变量。
本研究采用法兰取压方式,L1=L2=25.4/D,可膨胀系数的计算公式如式(5)所示。
(5)
式中:ε为可膨胀系数;p2为孔板下游压力,MPa;k为等熵指数,k=Cp/Cv;Cp为定压比热容,kJ/(kg·℃);Cv为定容比热容,kJ/(kg·℃)。
2 数值仿真模型建立及验证
2.1 孔板结构
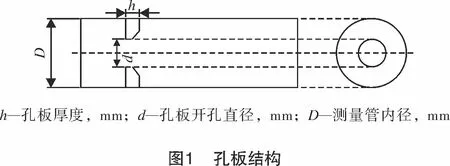
孔板结构示意图如图1所示。针对3种孔径比进行研究,孔板几何形状:孔板厚度为3.8 mm,孔板开孔厚度为0.8 mm,上游管径为150 mm,孔板孔径分别为57 mm、75 mm、87 mm,孔径比分别为0.38、0.50、0.58。本研究选择孔板上游直管段145D,下游直管段10D,以获得准确的模拟结果。
2.2 计算网格划分
采用ANSYS建立了标准孔板流量计的三维模型,利用六面体网格对网格进行划分。在模拟中,整个几何形状被分为3个区域:上游、中心区域、下游。上游和下游区域使用较粗网格,中心区域采用更密的网格,以获得压力梯度。墙附近的网格被细化,以满足标准墙功能的要求。管道模拟网格如图2所示。进行了网格尺寸独立性测试,用来确保数值模拟结果与网格尺寸和网格质量无关。以3 MPa下氢气摩尔分数分别为0.0、0.4的CH4-H2混合物为例,采用1 267 153、1 893 462、2 637 960、3 439 231个单元进行测试。网格数量从1 893 462增加到3 439 231时,网格数量对孔板前后的压力的影响已经很小了。考虑网格的无关性和计算效率,在以下模拟中采用2 637 960个单元的网格。

2.3 控制方程
假设:实际流体在管道中做定常流运动;气质组分为甲烷和氢气混合物,且混合均匀;流体在管道内与外界无热量交换。因此,除了满足质量、动量和能量三大守恒方程外,还需满足气体状态方程。本研究使用SRK状态方程[21],如式(6)所示。
(6)
式中:p为压力,MPa;R为气体常数,8.314 J/(mol·K);T为温度,K;V为摩尔体积,m3/mol;ac为临界参数,是临界温度和临界压力的函数;α为引力函数,是对比温度和偏心因子的函数;b为斥力函数。
还需分析甲烷和氢气在管道中气体传质规律,因此,开启组分输运模型[22],如式(7)所示:

(7)
式中:ρ为密度,kg/m3;ci为i组分的体积分数;t为时间,s;u为速度,m/s;Di为i组分的扩散系数,m2/s;Ri为单位时间、体积下产生i组分的质量,kg/(m3·s)。
针对天然气计量,还需结合湍流方程。k-εRNG模型在湍流模拟中得到了广泛的应用。与标准的k-ε模型相比,k-εRNG模型在表征具有强流线曲率、涡旋方面都有了显著的改进[15]。因此,本研究选择k-εRNG模型作为湍流方程。
2.4 边界条件
选择3 MPa压力边界进行计算。模拟的边界条件为:进口边界条件采用天然气压力,出口边界条件采用天然气出口流量。进口温度设置为303.15 K,流体介质采用甲烷和氢气混合物,并由软件本身的数据库确定了其密度、黏度等参数。令x(CH4)和x(H2)分别为甲烷和氢气摩尔分数,边界条件设置见表1。
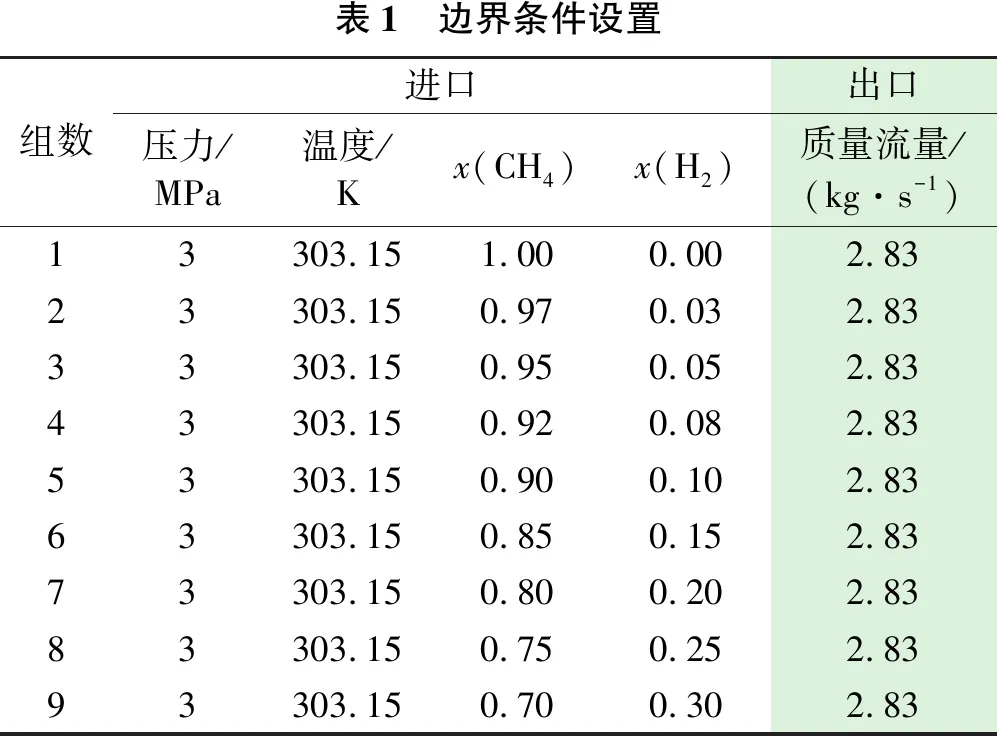
表1 边界条件设置组数进口出口压力/MPa温度/Kx(CH4)x(H2)质量流量/(kg·s-1)13303.151.000.002.8323303.150.970.032.8333303.150.950.052.8343303.150.920.082.8353303.150.900.102.8363303.150.850.152.8373303.150.800.202.8383303.150.750.252.8393303.150.700.302.83
2.5 有效性验证
基于流体相似原理,可利用Fluent计算在计量管内径为30 mm,孔径比为0.42、0.59、0.65条件下水的流出系数,与实验值进行对比,对本研究模型有效性进行验证[23]。验证结果如表2所列。
从表2可以看出,采用数值模拟方法计算出的流出系数与实验值吻合较好,偏差不超过-3.50%。
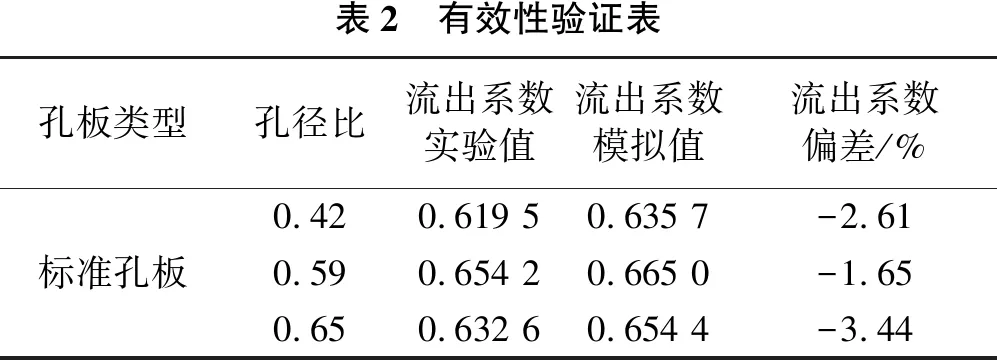
表2 有效性验证表孔板类型孔径比流出系数实验值流出系数模拟值流出系数偏差/%标准孔板0.420.619 50.635 7-2.610.590.654 20.665 0-1.650.650.632 60.654 4-3.44
3 结果与讨论
3.1 混氢量对差压的影响
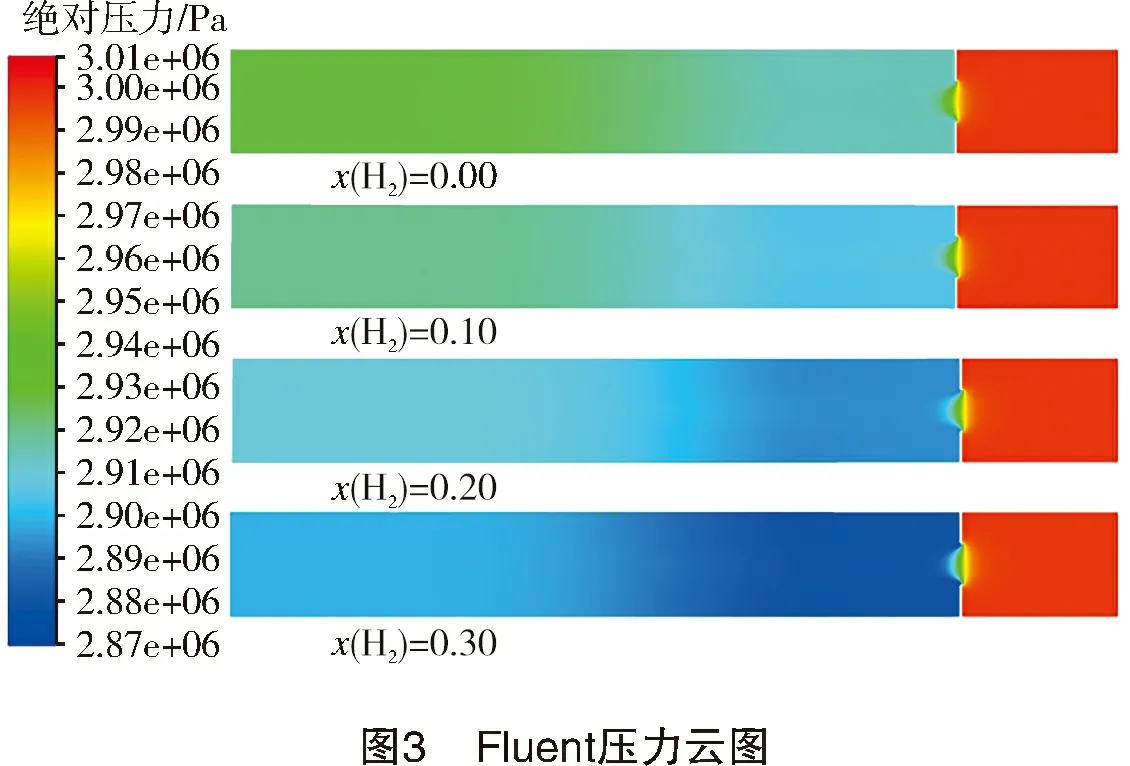
以孔板孔径比为0.38,x(H2)为0.00、0.10、0.20、0.30为例,Fluent仿真结果压力云图见图3。孔径比为0.38、0.50、0.58的标准孔板的差压随混氢量的变化如图4所示。
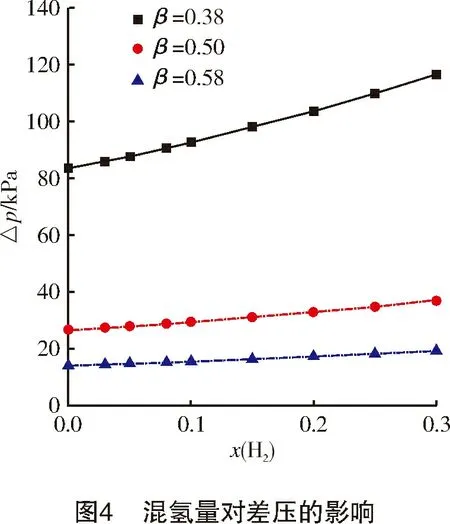
从图4可以看出,随着混氢量的增加,流过标准孔板的差压会逐步上升。从数值上看,孔径比越小,差压随混氢量的增加而上升的幅度越明显,这说明氢气对孔板的节流效应比较敏感。
3.2 混氢量对流速的影响
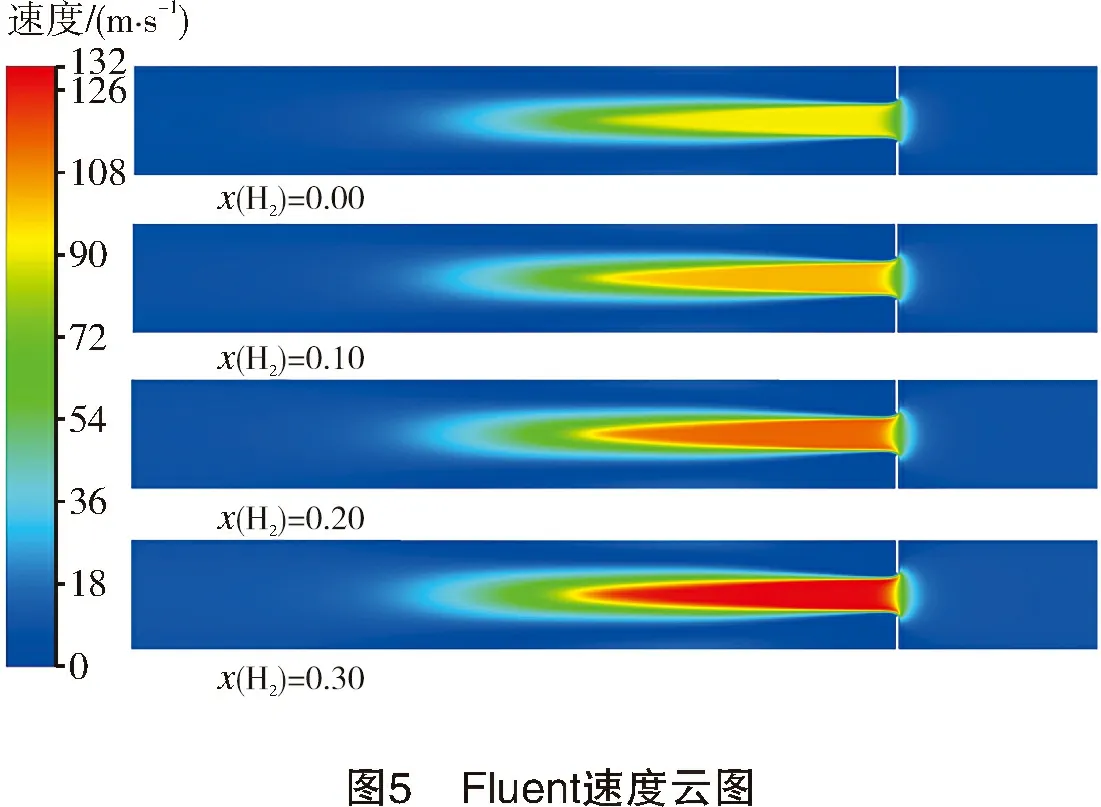
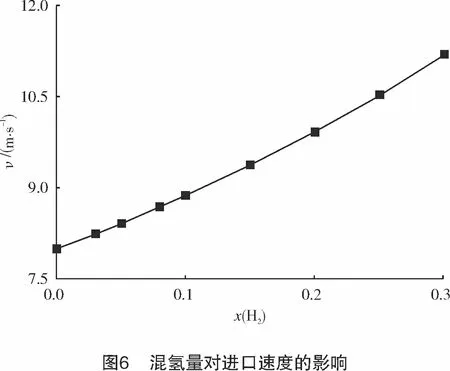
以孔板孔径比为0.38,x(H2)为0.00、0.10、0.20和0.30为例,Fluent仿真结果速度云图见图5。从图5可以看出,随着混氢量的增加,气流流过孔板后的速度更大。图6所示为混氢量与输送速度的关系图,从图中可看出,混氢量越高,流速越高。
因此,当天然气管道中掺入氢气后会导致流量增大。由于氢气的发热量小于甲烷,若仍然采用体积计量进行贸易交接,这将会对买方不利。若采用质量计量进行贸易交接,仍然不能合理体现掺氢天然气的实用价值,对供方不利。因此,针对混氢天然气,建议采用能量计量进行贸易交接。
3.3 混氢量对流出系数的影响
采用式(2)计算得到不同混氢量下的流出系数,计算结果见图7。从图7可以看出:孔径比越大,流出系数越大;在混氢量小于0.3时,混氢量的变化几乎不会对流出系数产生影响。

3.4 混氢量对相对密度系数的影响
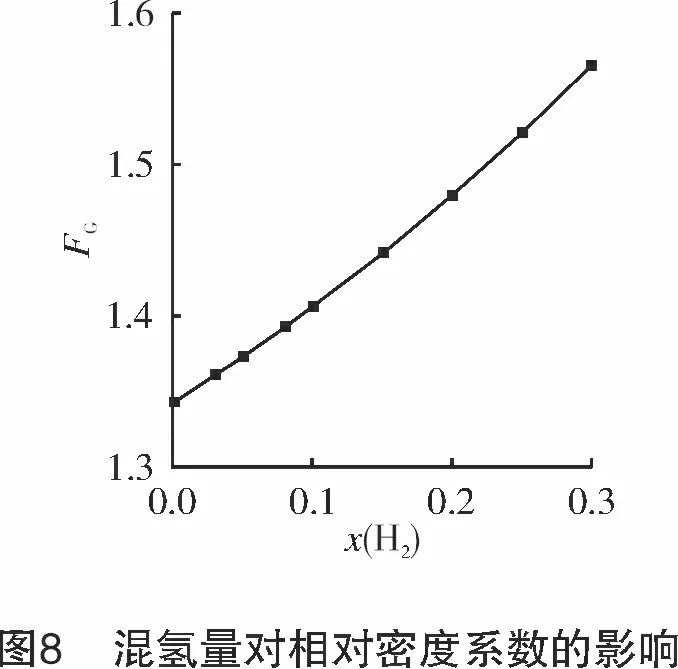
相对密度系数变化与孔板结构无关,仅与组分的变化有关,图8所示为相对密度系数随混氢量的变化情况。从图8可看出,混氢量的增加会导致相对密度系数上升,这是由于氢气的摩尔质量远小于甲烷,混氢量的增加会导致其摩尔质量下降,进而导致相对密度系数上升。
3.5 混氢量对可膨胀系数的影响
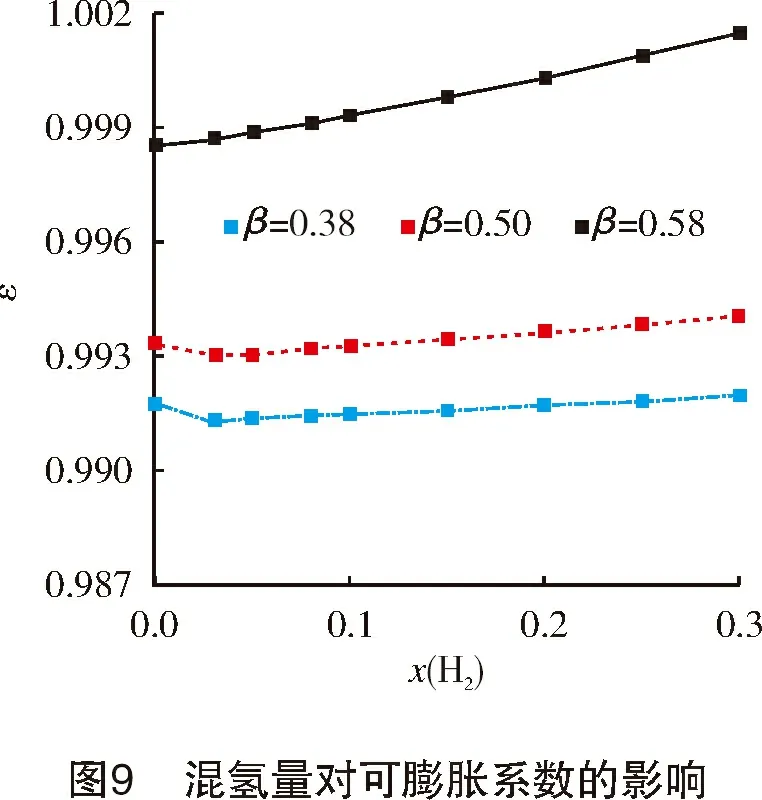
图9所示为可膨胀系数随混氢量的变化。从图9可以看出,随着混氢量的增加,会导致可膨胀系数下降,在低孔径比的情况下,其下降幅度要大于高孔径比,但整体下降幅度较小。
3.6 混氢量对超压缩系数的影响
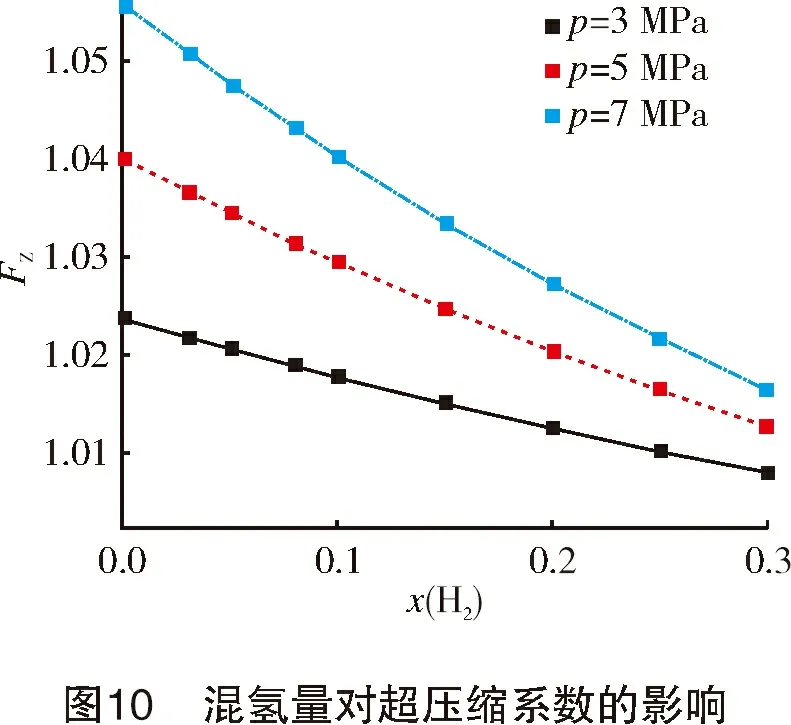
超压缩系数是因天然气特性偏离理想气体定律而采用的修正系数,其与孔板结构无关。分析在303.15 K,3 MPa、5 MPa和7 MPa条件下的超压缩系数随混氢量的变化(见图10)。从图10可以看出,超压缩系数随混氢量的增加而下降,压力越大,下降幅度越大。
3.7 混氢量对标准孔板流量计测量准确度的影响
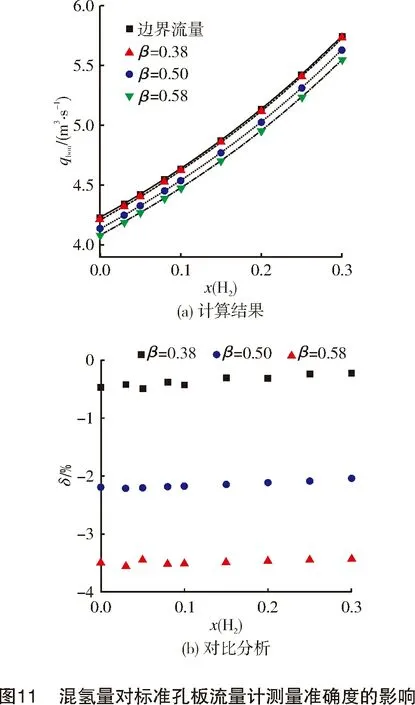
基于Fluent模拟结果,得到孔板前后压力、温度、黏度等参数,采用式(1)~式(5)计算得到的流量作为标准孔板流量计测量流量,以边界流量作为实际流量进行对比分析,分析结果见图11。基于本研究建立的计算模型得到标准孔板流量计的测量流量与管道截面的实际流量之间的测量误差,其计算公式如式(8)所示。
(8)
式中:δ为测量误差,%;qbou为实际流量,m3/s;qcal为测量流量(基于本研究建立的计算模型通过Fluent模拟计算得到的标准孔板流量计流量),m3/s。
从图11(a)可以看出随着混氢量的增加,标准孔板流量计测量流量也会显著增加。从图11(b)可以看出,标准孔板流量计计量准确度几乎不受混氢量变化的影响。
4 结论
采用数值模拟的方法,研究了标准孔板流量计应用于混氢天然气时的计量准确度。研究了混氢量对差压、流速、流出系数、相对密度系数、可膨胀系数和超压缩系数的影响,可得到以下结论。
(1) 在压力一定的情况下,混氢量的增加会导致体积流量测量的流量值增大。由于氢气的发热量小于甲烷,若采用体积计量进行贸易交接会对买方不利。因此,针对混氢天然气,建议采用能量计量进行贸易交接。
(2) 在压力一定的情况下,混氢量的增加会导致差压上升,导致相对密度系数、可膨胀系数和超压缩系数下降,而流出系数几乎不受氢气含量变化的影响。
(3) 将氢气掺入天然气管网,在氢气摩尔分数小于30%的情况下,氢含量的变化不会对标准孔板流量计准确度产生明显的影响。
