四向穿梭车作业调度模型求解优化及仿真

余嘉雄，白红星

(浙江凯乐士科技集团股份有限公司，浙江 嘉兴 314000)

近年来，为降低仓储成本，越来越多的企业选择四向穿梭车自动化立体仓库系统(以下简称四向穿梭车系统)来执行物品的出入库操作。在该系统中，多层高位货架的紧密放置，极大程度保证了仓库的空间利用率，使物品存储费用得以降低；物品的存取操作利用四向穿梭车和提升机配合执行，具有较高的取物速度和精准度。但是该系统还存在能耗低、系统稳定性不足、系统柔性低、任务执行速率低等问题。针对上述问题，已经有众多专家学者提出改进意见，如李丽等[1]从机构设计的角度对穿梭车进行优化，提高了穿梭车的稳定性；徐立云等[2]从穿梭车的冲突角度进行分析，提出道路定向调度策略，使出入库的效率得到提高；何昕杰等[3]对仓库物品进行编码，提出利用改进后的遗传算法对任务调度问题进行求解，实现对出库时间的精准控制。本文针对四向穿梭车任务执行速率低的问题，从穿梭车的冲突问题出发，通过改进作业时间调度的求解算法，提高作业调度对时间的精准把控，从而使四向穿梭车系统具有较高的任务执行速率。

1 四向穿梭车作业时间分析

1.1 四向穿梭车的作业流程

在四向穿梭车系统中，通过穿梭车和提升机之间的相互配合，即可实现对仓库货架上任意物品的出库操作[4]。四向穿梭车系统执行出库操作的流程：第一步，提升机运送空闲穿梭车至出库物品所在层；第二步，穿梭车前往物品对应的位置，取货并返回；第三步，提升机再运送载货穿梭车至出库层[5-7]。下面将分别对这三步流程进行分析。通过对穿梭车和提升机进行运动学分析，得到两者的速度和加速度的时间坐标图，如图1所示。

图1 穿梭车和提升机的速度、加速度时间坐标图

1.2 提升机接送空闲穿梭车时间模型

设提升机初始位于第x层，物品位于第y层。设置出库层位于第1层，则提升机位于第x层的概率P1(x)为：

(1)

式中：N为货架的层数。

由于物品的存储为随机放置，因此物品位于第y层的概率P2(y)为：

(2)

提升机从第x层移动至第1层的距离H1(x)为：

H1(x)=(x-1)h

(3)

式中：h为单个货位高度。

提升机从第1层移动至第y层的距离H2(y)为：

H2(y)=(y-1)h

(4)

结合图1可知，提升机从第x层移动至第1层的时间t1(x)为：

(5)

式中：aL为提升机加减速度；vL为提升机最大速度。

提升机从第1层移动至第y层的时间t2(y)为：

(6)

由此可知提升机接取空闲穿梭车并运送至物品层的平均时间MT1为：

(7)

式中：tL为提升机运送穿梭车的时间[6]。

1.3 穿梭车移动取物时间模型

穿梭车只能通过横向、纵向的导轨进行移动，因此设置合理的移动轨迹能极大程度地缩短出库时间。在常见的四向穿梭车系统中，一般为3个及以上巷道配置一个提升机。设AN为一个提升机服务的巷道数，当AN为奇数时，设提升机的初始位置在(AN+1)/2个巷道处；当AN为偶数时，设提升机的初始位置位于AN/2个巷道处。由于系统的出库位置随机，因此提升机取货需要移动z个巷道距离的概率P3(z)为：

(8)

执行单次取物操作，穿梭车的横向移动距离Dc(z)为：

Dc(z)=z(2l+WSD)

(9)

式中：l为单个货位的长度；WSD为穿梭车纵向导轨宽度。

执行单次取物操作，穿梭车的横向移动时间t3(z)为：

(10)

式中：aS为穿梭车加减速度；vS为穿梭车最大速度。

由式(8)可得，执行单次取物操作，穿梭车的平均换道时间tMCA为：

(11)

式中：tCA为穿梭车的换道时间。

假设物品的位置在第c列，执行单次取物操作，穿梭车的纵向移动距离DS(c)为：

DS(c)=c·W

(12)

式中：c为货架的列数；W为单个货位宽度。

执行单次取物操作，穿梭车的纵向移动时间t4(c)为：

(13)

因此，执行单次取物操作，穿梭车的平均运动时间MT2为：

(14)

式中：tS为穿梭车的换道时间；C为穿梭车单次取物操作移动的货架列数。

1.4 提升机接送载物穿梭车时间模型

设提升机此时位于第x层，物品位于第y层，提升机从第x层移动至第y层的距离H3(x,y)为：

H3(x,y)=|x-1|h

(15)

提升机从第y层移动至第1层的距离H4(y)为：

H4(y)=H2(y)=(y-1)h

(16)

提升机从第x层移动至第y层的时间t5(x,y)为：

(17)

提升机从第y层移动至第1层的时间t6(y)为：

t6(y)=t2(y)

(18)

因此，提升机接取载物穿梭车并运送至出库层的时间MT3为：

(19)

式中：P4(z)为提升机在第z层的概率；P5(y)为任务目标在y层的概率。

2 四向穿梭车系统任务调度研究

2.1 任务调度建模

通过上述流程分析可以看出，提升机的运输任务分为两种类型：一是接送空闲穿梭车，二是接送载物穿梭车。为保证货物进出库的总体效率，设定提升机接送空闲穿梭车A后，优先响应为停留在原地等待穿梭车A取物，在将载物穿梭车A接送至出库层后才能响应其他穿梭车的运输申请。为符合现场实际，设定出库层位于第1层，提升机的的初始位置也位于第1层。为避免穿梭车之间发生碰撞，一个巷道只允许一辆穿梭车进入，且默认本次取物结束时穿梭车和提升机的位置为下一次取件的初始位置。为计算方便，忽略穿梭车的交接耗时。

对于单次出库任务，设穿梭车在导轨上移动的总距离为SS，结合图1得穿梭车运行时间tSS为：

(20)

同理，设提升机运送穿梭车移动的总距离为SL，则提升机运行时间tSL为：

(21)

若穿梭车移动i列，则穿梭车在导轨上移动的总距离SS为：

SS=i·W

(22)

由于穿梭车的取物过程为一个来回，需要跨越两次巷道，因此穿梭车跨i个巷道取物的运行距离又可表达为：

SS=i(2l+WSD)

(23)

设穿梭车来回跨越巷道的数量为i和j，则穿梭车的横向运行时间tS,c为

tS,c=tS,c,i+tS,c,j+2g·tCA

(24)

式中：tS,c,i为穿梭车跨越i个巷道的时间；tS,c,j为穿梭车跨越j个巷道的时间；g=i+j，取值范围为0，1，2。

若某任务位于第p层，则提升机执行该任务需要移动的层数为2p，结合式(15)、(16)，可得提升机执行该任务的SL为：

SL=2|p|h

(25)

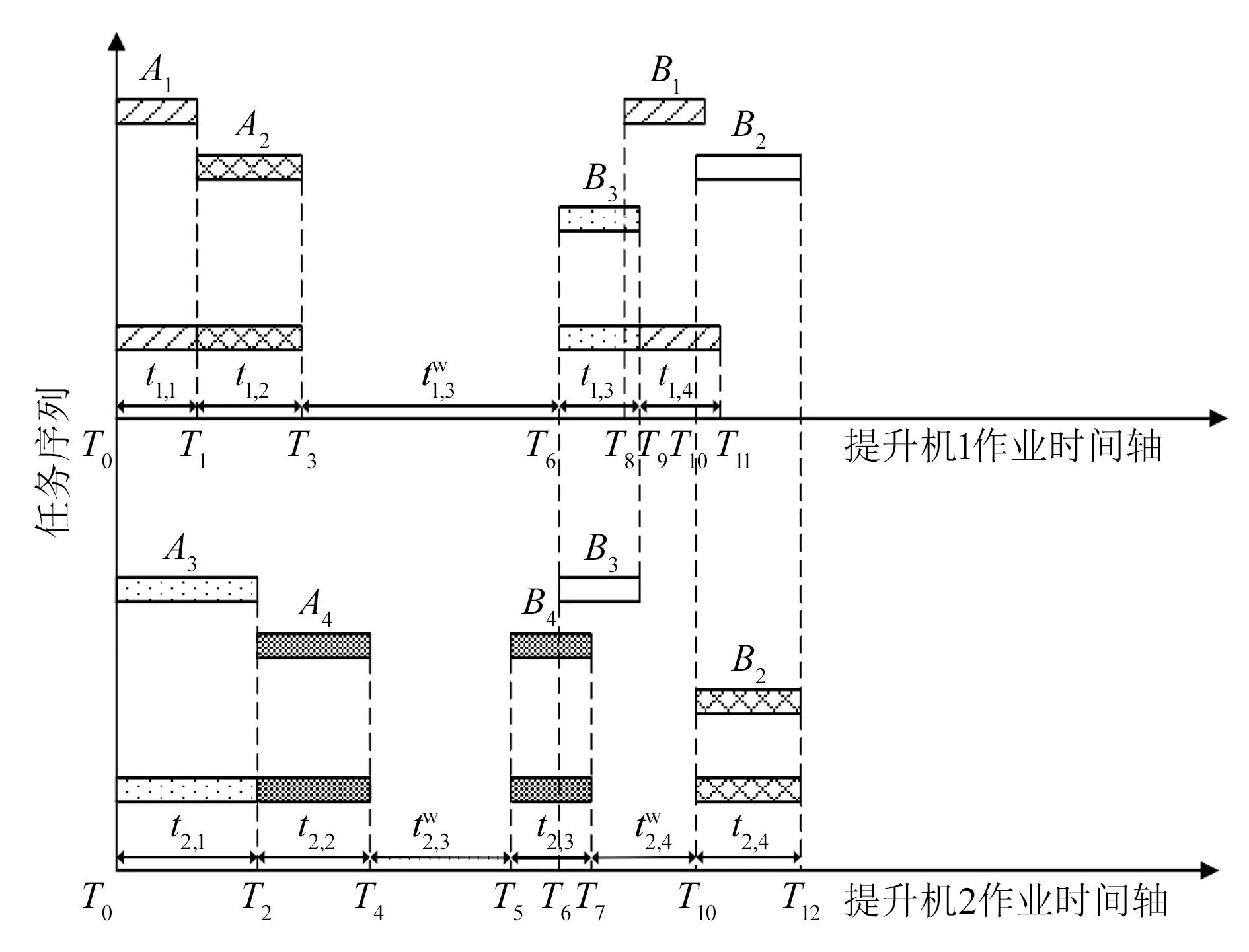
图2 提升机出库作业时序图

设某提升机编号为K。由图2可得，K执行第m个任务所需时间tK,m为：

(26)

计算提升机K完成第m个任务的时刻TK,m为：

(27)

(28)

分析穿梭车的取货过程，结合图2可知，提升机执行所有出库任务的总用时Ttotal为：

(29)

式中：M为执行任务的总数。

式(29)即为任务调度模型的目标函数[7]。

2.2 系统冲突解决策略

四向穿梭车系统中，穿梭车有相向冲突、节点冲突、同向冲突、追及冲突4种冲突类型。为实现运送过程中的冲突类型判断，从左到右将横向导轨上的节点、路径依次进行编码，对于处在同一层的多个穿梭车，构建冲突路径和时间的路径时间窗。假设一个四向穿梭车系统中有2个提升机、6组货架，构建的路径时间窗如图3所示。

由于从图3中可以直接得到容易出现冲突的节点，因此需要基于迭代时间窗构建冲突消除模型，即将穿梭车的时间窗进行整体移位，进而消除冲突。首先判断发生冲突的穿梭车的任务等级，将任务等级低的穿梭车进行整体时间窗移位；对于同任务等级的冲突，根据到达冲突位置节点的时间顺序，将后到的穿梭车进行整体时间窗移位。

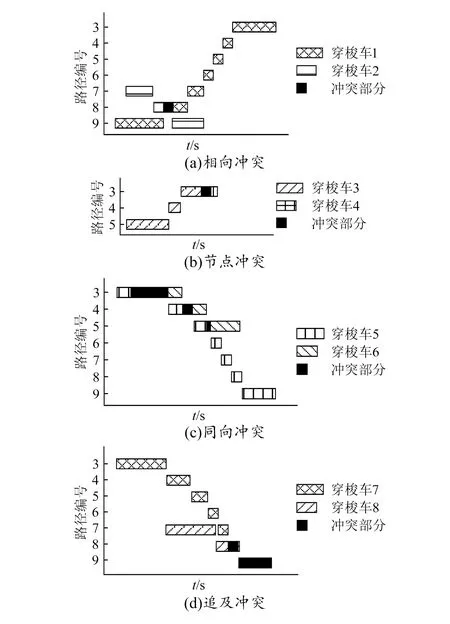
图3 基于路径时间窗的冲突判断

1)当出现相向冲突或节点冲突时，系统可能出现死锁，其移位过程如下：

①先找到发生冲突的节点，并推算需要进行移位的穿梭车的上一节点位置。

②计算两个穿梭车到达冲突节点的时刻，设两个不同的优先级时刻分别为T2和T1，则移位时刻tm为：

tm=T2-T1+t0

(30)

式中：t0为穿梭车安全缓冲时长，根据穿梭车和系统反应时间自行设定。

③将移位穿梭车的整体时间窗向后移动tm时刻。

2)对于同向冲突和追及冲突，可以直接将后抵达冲突节点的穿梭车进行移位。其移位过程如下：

①寻找存在冲突的路径和节点。

②计算所有冲突时长，记最大值tc,max，得移位时长为：

tm=tc,max+t0

(31)

③将移位穿梭车的整体时间窗向后移动tm时刻。

基于上述分析，设计避免冲突等待时间的计算流程，如图4所示。

2.3 系统任务调度优化

由于四向穿梭车的系统任务调度主要是指定提升机对穿梭车进行运送，对于这类问题，传统的离散粒子群算法无法直接应用，需要进行相关优化[8]。

假设四向穿梭车系统中存在2个提升机，需要将8个物品出库，为实现物品定位，对物品序号和维度进行编码，X-Y表示第X号物品第Y个维度，随机选取8个物品的坐标，并分配给提升机，得到图5。

图5 物品编码与提升机分配

在此，引入同维度粒子位置块[9]，将提升机中同一维度中的所有序号作为一个整体，即位置块，再利用离散粒子群算法，对编码进行速度作用，引入速度算子[10]。设物体的移动速度中包含多个速度算子，将速度算子V={0,0,2,0}作用于图5，得到图6所示转换图。

图6 速度算子作用转换图

按照图6所示的方法将位置块的位置进行转换，可以实现对提升机传送穿梭车的顺序优化。由于速度算子的作用是将整个维度进行整体移动，因此维度编码对任务调度影响较大。为解决不合理的维度编码导致任务调度中各提升机无法收敛的问题，需要对维度编码[11]进行研究。

由于在四向穿梭车的实际应用中，货架列数一般远大于货架层数，因此任务调度中出库任务的列数影响较大。为此，本文根据列数排序与维度编码进行匹配，当列数相同时，优先对序号小的进行出库[12]。以30个出库任务为例，设共有50列货架，将各提升机与需要执行的出库编码进行配对[13]，得到表1。

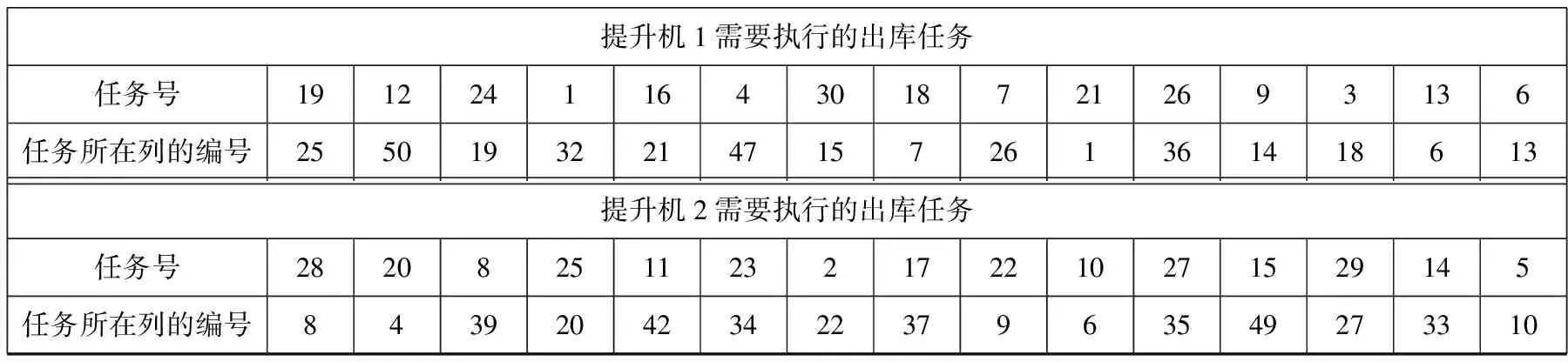
表1 30个出库任务与其对应的提升机任务

根据上文所述方法对表1中的内容进行编码，得到的初始编码如图7所示。

假设最优的速度算子V={0，1，0，0，0，0，3，0，0，0，5，0，0，8，4}，根据上文的位置块转换方法，可对图7的编码进行转换，得到图8所示的编码。

图7 根据列数排序得到的初始编码

通过算法计算可以得到同维度间发生位置互换的概率pe。设pe=2，对图8所示编码进行同维度位置互换，得到图9所示的编码。

图8 根据最优的速度算子转换得到的编码

图9 同维度位置互换所得的编码

为得到完成任务的最大时长，使数据最为可靠，本文将任务均分给2台提升机，即每一台提升机任务执行量相等。为极大地降低任务耗时，任一个任务都选择预测路线最短的提升机。

由于传统的离散粒子群(discrete particle swarm optimization，DPSO)算法只能单独得到个体最优值，不同个体间缺少交流，在迭代后期，容易丧失局部搜索能力。为解决这类问题，本文将对DPSO 算法进行改进。改进步骤如下：

1)在进行迭代的过程中，从位置块中随机选择编码，编码i被选中的概率为Ps,i。

2)引入遗传算法(genetic algorithm,GA)中的选择交叉操作，将随机选中穿梭车来回跨越巷道的数量编码i和编码j两两配对，按照概率Pc进行随机交叉互换，保留交叉前后适应值较高的编码组。

交叉互换中各编码互换示意图如图10所示。

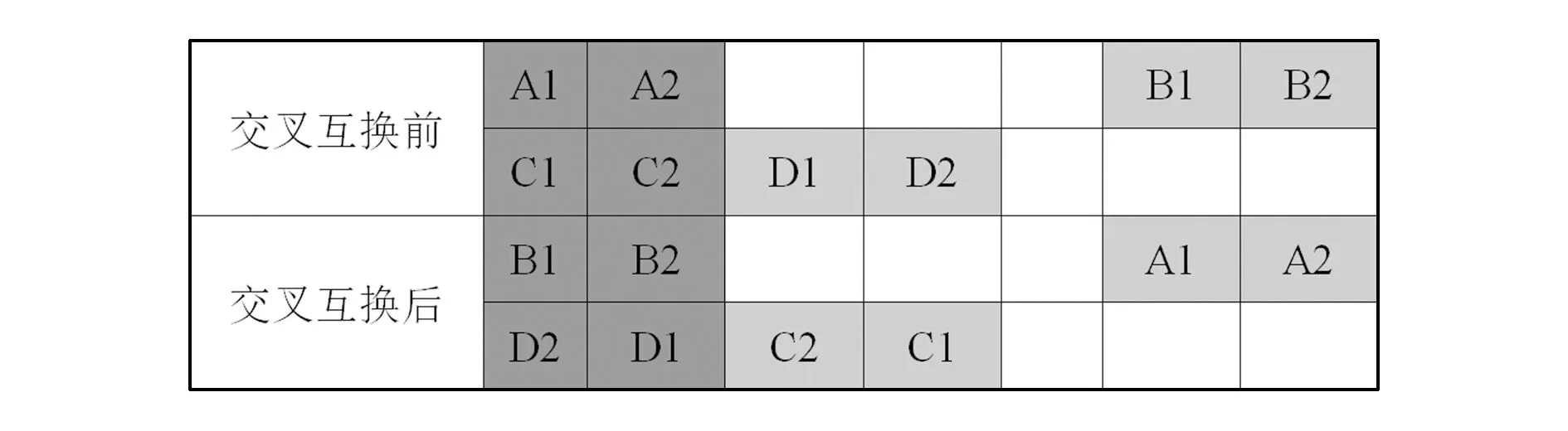
图10 交叉互换中各编码互换示意图

编码进行交叉互换操作时，首先选取维度不同的几组编码，使其位置块交叉互换。其次引入遗传算法中的变异操作[14]检测全局极值，当编码组无法进行迭代改善时，对该编码组所有编码进行初始化操作，即随机重组分配，概率为Pv。

基于GA-DPSO算法的流程图如图11所示。

图11 基于GA-DPSO算法的流程图

改进后的GA-DPSO算法能够实现各编码间的信息交流和共享，且能够更快得到目标函数的最优解，具有较高的收敛速度，在迭代后期，搜索能力也不会降低。

3 实例分析

由于提升机数量和穿梭车数量都会对任务调度速率造成影响，因此在实际的单个作业中，一般配置2个提升机和8个穿梭车进行调度求解。本文选取某物流仓库为实验对象，随机提取50,100,150个出库物品，并对其编码。再根据优化后的算法计算出概率、时间、速率等具体参数，将这些参数输入任务调度模型即可得到任务调度结果。为验证本文改进后的GA-DPSO算法的效果，引入传统DPSO算法和GA算法，将3种算法的任务调度结果进行对比，得到表2。

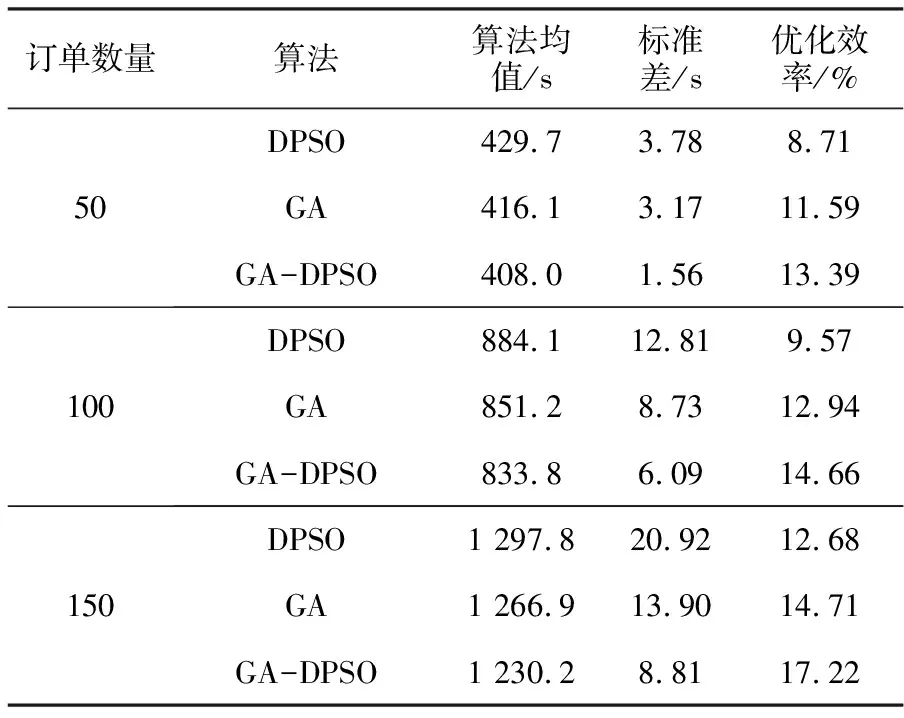
表2 不同订单数量下3种算法的调度结果

从表2可以看出，GA-DPSO算法的均值和标准差都最小，优化效率最高，由此可以证明本文改进的GA-DPSO算法具有更高的执行速率、更高的稳定性和更好的优化能力。

基于表2，绘出不同订单数量下3种算法的迭代曲线，如图12所示。

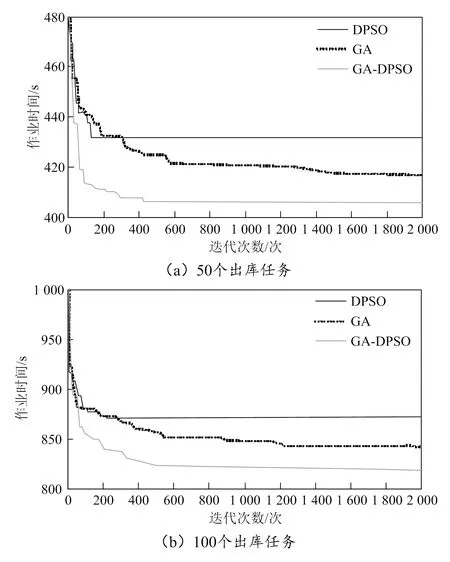
图12 不同订单数量下3种算法的迭代曲线

从图12可以看出，本文改进的GA-DPSO算法具有更快的迭代收敛速度，且由于引入了交叉变异操作，更容易得到全局最优解。

综上所述，本文改进的GA-DPSO算法基本能够实现设计要求，能够有效地提高四向穿梭车系统运行的稳定性。

4 结束语

综上可知，优化后的四向穿梭车作业调度模型求解算法具有较高的稳定性，能够有效提高四向穿梭车系统的出入库效率，具有一定的应用价值。但本文并未涉及穿梭车和提升机的移动速度突变等情况的误差修正，在四向穿梭车系统连续作业超过一定时长后，会出现调度优势减弱的情况，因此需要定期进行系统重启或调度清零操作；且本文只对四向穿梭车作业调度模型求解算法进行优化，并未对调度模型和穿梭车进行改进，因此还有很大的改进空间。