基于迭代离散度序贯检测的航迹抗差关联算法
2022-08-18国佳恩
关 欣, 国佳恩
(海军航空大学, 山东 烟台 264001)
0 引 言
在分布式多传感信息融合系统[1-2]中,航迹关联是研究如何将不同传感器上报的航迹进行同源性匹配的问题。由于航迹的异步及系统误差的存在[3],使得航迹关联难度增大,要获得可靠的关联结果就必须针对上述问题进行解决。
无需系统误差校准直接进行航迹的抗差关联[4-6]一直是解决带差航迹关联问题的有效手段。通过定义广义时空交叉点并采用特征匹配方法,文献[7]实现了具有强鲁棒性及稳定性的航迹抗差关联。文献[8]采用基于密度的模糊聚类思想[9-10],将误差带来的不确定性模糊化,所提方法的关联结果接近贝叶斯最小均方误差准则的结果,且有效降低了计算开销。文献[11]则基于刚性变换函数[12]推导出一种新颖的多参数代价函数,根据自适应进化策略算法有效估计系统误差实现带差航迹的精准关联。文献[13]引入一种基于相干点漂移的概率方法,并使用期望最大化(expectation-maximum, EM)算法估计局部航迹间的匹配矩阵[14],用于解决系统误差下的航迹关联问题。针对现有抗差算法对海上目标应用效果不佳的问题,文献[15]利用海上目标稳定的拓扑关系,基于三角形稳定结构[16]设计了适用于海上目标的航迹抗差关联算法。文献[17]利用高斯随机矢量的统计特征,提出顺序成对关联思想。文献[18]则利用真实状态对消得到等价量测方程,进行分级聚类。
解决航迹抗差关联的另一种思路是根据系统误差的先验知识,对系统误差约束下的目标航迹作区间不确定化处理。基于该思路,文献[19]用区间灰数描述目标航迹,并定义区间运算来实现抗差关联,但算法运算效率偏低。文献[20]提出一种基于层次聚类分析的抗差航迹编组算法;文献[21-22]分别采用航迹的参考拓扑特征、拓扑统计距离描述航迹的不确定性,利用非刚性变换描述航迹间的结构差异。文献[23]建立了混合整数非线性规划模型进行航迹关联。基于t分布混合模型,文献[24]将航迹关联问题转化为图像匹配中的非刚性点集匹配问题。针对雷达与电子支援设施航迹的抗差关联,文献[25]基于高斯随机矢量统计特性,提出一种基于航迹矢量检测的雷达与电子支援措施(electronic support measures, ESM)航迹抗差关联算法。文献[26-27]则分别定义了区间离散度及概率区间离散度来模拟系统误差的影响。
然而,上述算法均是基于批处理的关联方式,即需要获取固定数目的航迹点数或在融合周期末进行关联,缺乏对航迹整体信息的利用,且单次关联的运算量较大从而导致耗时较长,尤其是当目标密集且运动速度较快时,传统的关联方式实时性明显变差。同时,区间不确定化的处理方式丢失了误差的分布信息,虽能解决航迹的抗差关联但不符合量测实际及直观认知,用量测值反推真值的方式也缺乏一定合理性。此外,目前缺乏大误差背景下对大批量航迹数据进行准确关联的研究,因此如何应对多目标、大误差等复杂条件下的航迹关联是当前的一个难题。
基于此,本文着重从航迹的稳健抗差关联着手进行算法的创新,提出一种基于迭代离散度序贯检测的关联算法,改进原离散度的求解思路,采用迭代的方式推导所有关联时刻离散度的概率分布,并用基于误差重构的随机量测量改进原有的区间方式进行抗差关联,借鉴信号检测中的序贯思想对离散度进行序贯关联以克服单次关联判定的偶然性,同时可以弱化误差在关联判定中的影响,因此相同条件下可对大误差背景下的航迹进行准确关联,在目标编队飞行导致航迹大量分叉合并等特殊情况下亦可取得较好的关联效果。
1 问题描述
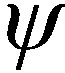
(1)
(2)
航迹关联要解决的问题就是将来自不同传感器的航迹数据进行同源性辨析[28],以判别其是否来自同一目标,为下一步的航迹融合与目标跟踪提供依据。
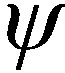
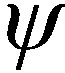
H={H1,H2,…,Hn}
由此便将航迹关联转换为统计数学中的假设检验问题[29]。
2 基于迭代离散度序贯检测的航迹抗差关联算法
2.1 离散度迭代求解
航迹异步是由于不同雷达传感器扫描周期及开机时刻存在差异导致的,因此一个融合周期内来自不同雷达传感器上报的航迹数据一般呈交叉分布[30],第e个融合周期内的异步航迹上报过程如图1所示。

图1 航迹异步上报过程示意图Fig.1 Schematic diagram of asynchronous track reporting process
假设各传感器侦测航迹数据非实时上报,待一次扫描结束后统一上报,将融合中心接收第k批航迹上报的时刻定义为第k个关联时刻,则一个融合周期共有K=INTL[T/T1]+INTL[T/T2]个关联时刻,其中INTL[x]表示不大于x的最大整数。
根据文献[27],混合航迹序列在第k个关联时刻的离散度的定义为
(3)
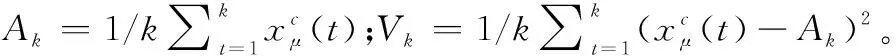
不难发现,文献[27]定义的离散度实质上就是利用方差及均值分别表征混合航迹序列的离散程度和几何中心,进而实现同源航迹的关联判别。从原理来看,方差在航迹关联判别中起到主要的区分作用,因此本文直接将方差作为混合航迹序列的离散度,并结合序贯检测思想给出离散度的迭代求解方法。
为充分利用航迹的历史信息,本文借鉴信号检测中的序贯思想对原式进行改写,给出迭代离散度的运算方法,其表达式为
(4)
其中,
可以看出,仅依靠上一关联时刻的离散度及当前时刻的航迹数据便可迭代求解当前时刻离散度,且在不增加运算量的前提下获取了混合航迹序列所有关联时刻的离散度数据,可实现边观测边关联,相比批处理方式更具实时关联优势。
矩阵行向量为不同混合航迹序列的迭代离散度序列,列向量为各混合航迹序列在同一关联时刻的迭代离散度。
2.2 带差航迹序列的离散度分布
考虑目标观测过程中受到雷达传感器系统误差及随机量测误差[31-32]等影响,量测量实质上是在一定误差范围内具备某种分布特征的随机变量,基于式(4)推导的离散度亦应视作含有误差信息的随机值,下面用随机量测量代替量测值进行航迹关联问题讨论。
已知传感器的量测方程为
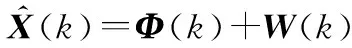
(5)
由于量测过程存在不确定性,假定量测值在以系统误差最大值Δxm为边界的对称区间内服从高斯分布,即
(6)
(7)
得到带差航迹的随机量测表示后,将第k个关联时刻混合航迹序列离散度的分布情况以定理1形式给出并给出证明。
定理 1最大系统误差及随机量测误差共同约束下的混合航迹序列在第k个关联时刻的迭代离散度服从自由度为k的非中心χ2分布,概率密度为
(8)

证明已知正态分布N(μ,σ2)的特征函数为
(9)
则第k个关联时刻量测量的特征函数满足
(10)
由于量测量的随机性源于系统误差及量测噪声,而量测噪声在不同时刻互不相关,且系统误差是相互独立的高斯随机量,因此不同时刻的量测量亦相互独立。当变量α,β相互独立时,两变量线性组合k1α+k2β的特征函数满足φk1α+k2β(t)=φα(k1t)·φβ(k2t),依据此性质,对均值进行迭代求解,得到混合航迹序列均值的特征函数:
(11)
初值满足
(12)
均值是不同时刻量测量的线性组合,依据式(11),得到第k个关联时刻混合航迹序列均值的特征函数:
(13)
由于离散度的定义涉及非线性运算,无法直接应用特征函数性质进行迭代求解,为此,将式(11)直接代入离散度的原始定义式中,得到第k个关联时刻混合航迹序列离散度的特征函数为
(14)
其期望满足
(15)
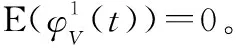
(16)
将式(13)代入式(16)进行积分运算后再取微分,得到离散度的概率密度函数:
(17)
证毕
得到离散度的概率分布后便可进行关联航迹的假设检验。
2.3 航迹关联判决及序贯检测
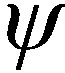
(18)
似然函数中的未知量为不同时刻的离散度真值λ1,λ2,…,λk。已知系统误差对航迹的影响表现为航迹整体的旋转平移,因此在航迹量测基础上迭代得到的离散度与航迹序列真实离散度的偏差可视作旋转平移量的迭代离散度,由于系统误差具有缓变特性,在一段时间内保持相对稳定,因此真实量与量测量之间的偏差为非时变固定偏差,且在不同混合航迹序列间具有一致性,因此可将式(17)中的λk进行等效替换并进行最大似然检验以确定假设Hj是否成立。
下面根据检测终点的不同给出序贯检测方式下两种关联判定准则。
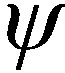
(19)
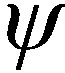
(20)
此时,认为接受Hj。
结合传统的二维分配算法给出全局求解方法:
(21)
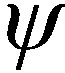
或者设定检测阈值Λ0,从第一个关联时刻开始进行最大似然检验,若满足阈值条件则当前航迹关联结束。如果不能做出决策或者存在关联多义性,则继续观测接收航迹数据,按照同样的方法进行关联判决,直至所有航迹关联结束。其中,阈值Λ0满足
(22)
该种关联判定准则的最大优点是,在给定的似然函数检测门限下,其所依赖的航迹数据较少,即平均检测时间较短,但由于需在每个时刻进行关联判决,因此计算量高于传统方法。
由于多传感器航迹关联是在双传感器航迹关联上的简单扩展,且本文采用了二维分配方式进行关联判定,因此可借鉴文献[27]算法将本文算法进一步扩展到多传感器领域,利用多维分配进行航迹的关联判定,由于其原理及求解过程与二维分配基本一致,本文不做相关赘述。
基于离散度序贯检测的航迹抗差关联算法的流程如图2所示。
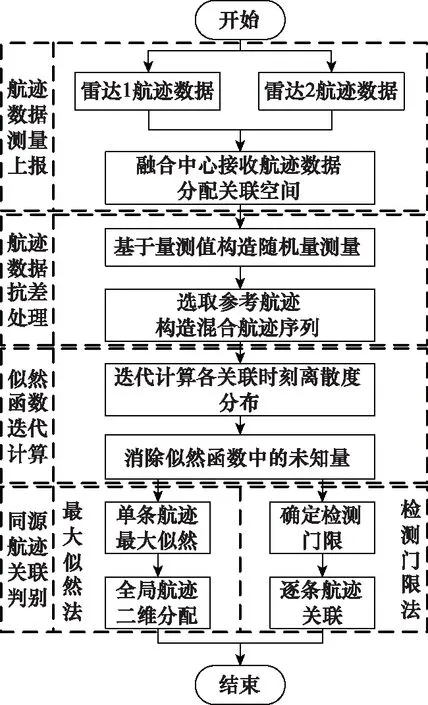
图2 本文算法流程Fig.2 Process of the proposed algorithm
3 仿真分析与检验
为验证本文算法的抗差关联效果,仿真中将其与文献[19,26-27]算法进行对比检验。3类算法均采用区间化方式对误差存在下的量测量做不确定化处理,其思路是用量测航迹对真实航迹进行反推,认为真实航迹在以量测量及系统误差构造的闭区间内随机分布。不同的是,文献[19]采用区间相离度衡量不同航迹的相似程度,而文献[26-27]则结合离散度分别设计了区间离散度及概率区间离散度衡量不同航迹的相似性。需要指出的是,3类算法的区间化处理方式都是“由果溯因”的反推过程,若采用单侧区间化,则有0.5的概率无法覆盖真实航迹;若采用双侧区间则额外引入了不必要信息,大大降低了关联精度,因此用区间反推的方式缺乏一定合理性,导致关联效果不佳。本文算法采用推导的方式获取航迹的真实分布情况,用变量运算代替区间运算,可克服区间处理的不确定性,迭代运算的设计使得关联判定阶段可以充分考虑航迹的历史信息,可以有效提升关联效果。
3.1 仿真环境
3.2 算法序贯检测效果分析
首先对本文给出的第二类序贯判决准则进行检验。预设不同的似然检测门限,观测给定仿真条件下的关联效果。
从表1 可以看出,随着检测阈值的增大,完成关联解算的时间也在增大,这是由于阈值的大小约束了航迹检测的点数,阈值越大,关联判定所需的航迹数据越多,因此关联运算时间越长。同时,参与航迹关联的航迹数据的增多带来了更佳的关联效果,使得关联正确率也有所提升。
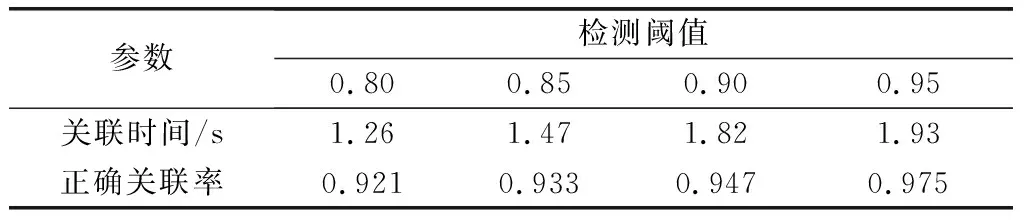
表1 不同检测阈值下的关联结果
图3是本文算法及文献[19,26-27]所述抗差关联算法在不同观测时间下的仿真结果。

图3 正确关联率随仿真时间步长变化情况Fig.3 Change of correct correlation rate with the simulation time step
可以看出,本文所述的抗差关联算法在两类序贯检测准则下均取得了最佳关联效果。文献[26-27]已验证了应用离散度进行航迹关联求解的优势,而本文算法在离散度的基础上通过迭代运算获取了不同时刻的离散度信息,将航迹的历史信息纳入到航迹关联判定中,实现航迹的序贯检测,避免了传统的一次关联判定带来的误关联问题,可有效提升航迹关联效果。
其他仿真条件不变,改变仿真条件中的目标数量,观测不同目标航迹数对算法性能的影响,如图4所示。

图4 不同目标数的正确关联率对比Fig.4 Comparison of correct correlation rate of different target numbers
区别于几何距离,离散度是刻画数据离散程度或聚集程度的范数度量,在航迹密集条件下,由于离散度的固有属性限制,不可避免地导致误关联的增加,使得在目标数量增多时文献[26-27]算法关联性能下降;文献[19]采用区间相离度衡量区间灰数的相似性,区间灰数是在量测值基础上进行的区间重构,在实现抗差关联的同时也损失了一定的关联精度。从图4可以看出,本文算法在不同目标数目下均保持了较高的关联准确率,较已有算法性能提升显著。
3.3 算法抗差关联性能分析
为检验本文所述算法在无系统误差预先配准情况下的抗差关联性能,其他仿真条件不变,改变传感器的量测误差及系统误差,观测不同条件下的关联准确率。同样,基于离散度进行航迹关联,文献[26]已验证了算法对不同噪声分布形式的关联鲁棒性,因此下文着重对不同误差水平下的算法效果进行检验。
默认雷达1的系统误差不变,改变雷达2的系统误差,得到不同测距误差下各算法的关联结果,如图5所示。
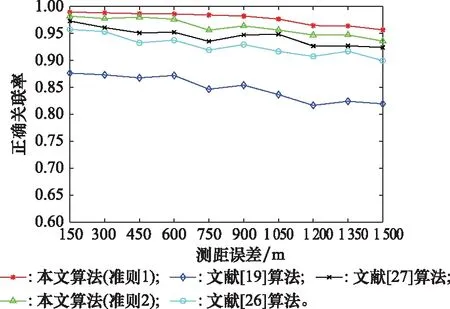
图5 不同测距误差(系统误差)关联结果Fig.5 Correlation results of different range measurement errors (system errors)
本文算法是将量测值视作带差的随机变量,并在推导所得的离散度分布的基础上进行的航迹序贯检测,将量测值随机化可有效将系统误差纳入到航迹关联判定中,实现航迹的抗差关联,区别于文献[19,26]用最大系统误差约束下的均匀分布区间的航迹描述方式,本文算法在原理上更符合实际量测过程的直观认知。同时,序贯检测的引入避免了局部异常数据导致的错判漏判,从航迹全局的角度实现了航迹的关联判定。从图5的仿真结果可以看出,本文算法在大系统误差下仍能保持95%以上的正确关联率,优于现有抗差关联算法。不同测角误差下各算法的关联结果如图6所示。

图6 不同测角误差(系统误差)关联结果Fig.6 Correlation results of different angle measurement errors (system errors)
可以看出改变测角误差后算法的正确关联率略有下降,但趋势并不明显。结合测距误差的关联结果来看,本文算法在抗系统误差对关联的影响上相比文献[19,26-27]算法更具优势。
其他仿真条件不变,同时改变随机量测误差中的距离及角度误差,研究随机量测误差对算法性能的影响。
从原理来看,随机量测误差与系统误差对关联的影响具有一致性,但尺度更小。从表2可以看出,在不同距离及角度误差组合下,本文所述算法在两种关联准则下关联效果相差不大,相同仿真条件下对比其他算法具有最佳的关联准确率。
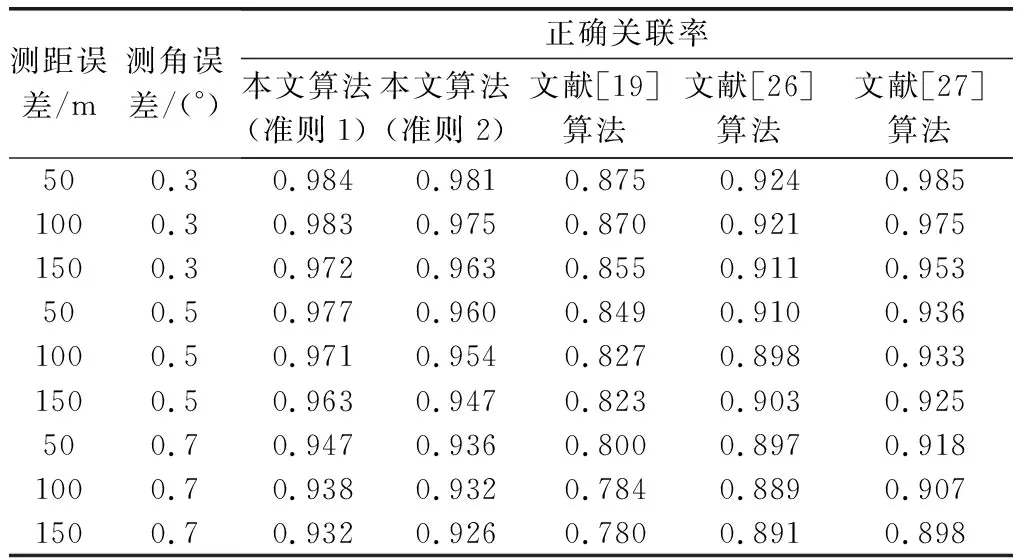
表2 不同量测误差组合正确关联率对比
3.4 算法运算量分析
改变仿真条件,从运算效率的角度继续检验不同算法的运算复杂度。
在其余仿真条件不变的情况下改变观测区域内的目标数目,得到不同算法完成全局航迹关联运算所需时间对比,结果如图7所示。由于采用了迭代的方式求解离散度,在进行相似性测度求解时,本文算法仅需利用关联前一时刻的离散度及当前时刻航迹数据便可递推得到当前时刻的离散度,迭代的运算方式使得融合中心的数据存储压力大大减小,运算效率较传统算法提升十分显著,可较好地应对密集航迹背景下的航迹关联问题。其他仿真条件不变,改变两部雷达传感器对指定观测空域的观测时间,获取不同规模的航迹数据,检验算法在航迹数目不变、航迹长度改变下的系统运算时间如表3所示。可以看出,本文算法的运算效率要优于文献[19,26]算法,这是由于文献[19]算法需经过区间灰数化、区间相离度解算及灰关联度求解排序等多步运算方能完成单次关联判定,而文献[27]算法则涉及大量积分运算,因此关联效率均不高。同时可以看出,本文算法同等条件下耗时要长于文献[26]算法,这是由于当观测时间增大时,航迹长度随之递增,要完成序贯检测就需要在所有关联时刻进行关联判定,且似然估计阶段亦增加了部分运算量。

图7 不同目标数目运算耗时对比Fig.7 Comparison of computation time of different target numbers
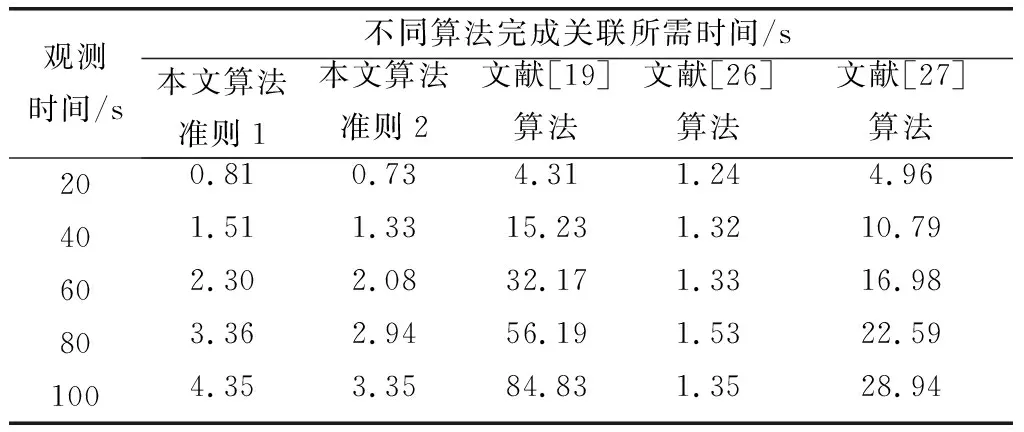
表3 不同观测时间运算耗时对比
3.5 对航迹交叉的辨别
复杂空域环境下,大量飞行目标高速机动往往导致航迹大量交叉,大大提升了关联难度。通过仿真条件设定不同的航迹交叉比率,检验不同算法在复杂情况下的关联性能。
从图8可以看出,由于本文所述算法采用了序贯检测,航迹历史信息被考虑进来,因此可更好的克服航迹交叉,在不同航迹交叉率下可保持较为稳定的关联准确率,在应对航迹交叉等特殊情形下要优于文献[26-27]采用的航迹分段方式。
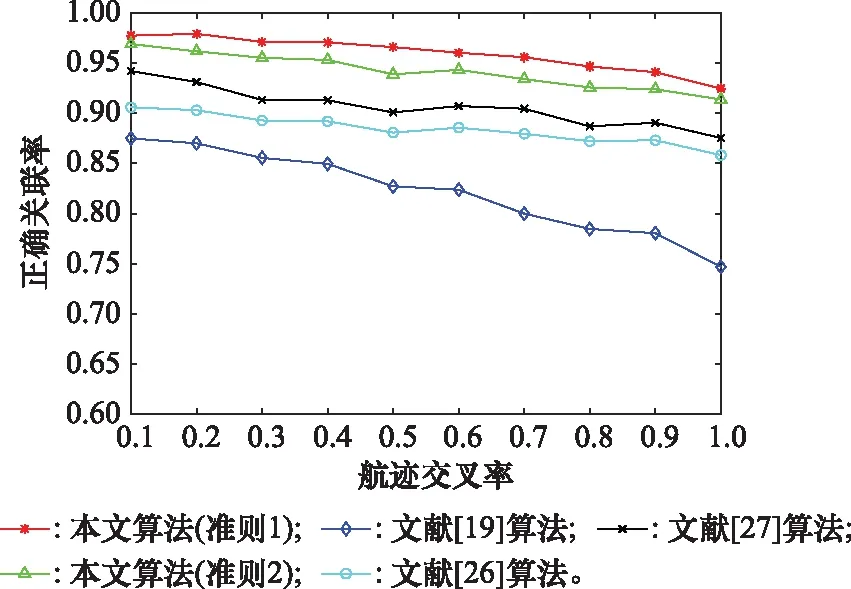
图8 不同航迹交叉比例关联结果Fig.8 Correlation results of different track cross ratio
4 结 论
本文提出一种基于离散度序贯检测的航迹抗差关联算法,采用迭代的方式推导出不同时刻的离散度分布,并在此基础上给出了两种关联判定准则进行航迹的序贯检测,实现了航迹的抗差关联,同时克服了批处理方式因单次关联导致的对航迹信息利用不足的弊端。
通过不同的仿真算例表明,本文所述算法在大系统误差、密集目标大量交叉等复杂场景下均能实现较高的关联准确率,验证了算法在抗差关联、关联精度及关联速度上的优势。且在关联判定阶段采用了二维分配算法,因此可以很好地扩展到多维分配并应用到多传感器的航迹关联。
由于实际战场环境下的量测条件趋于复杂,而本文则基于标准高斯分布对量测噪声进行仿真,对实战环境下算法的关联效果还有待进一步检验,下一步将引入实测数据验证本文算法并加以改进,增强算法适用性。
