负压梯度下自由面流动模拟的无网格粒子法Dirichlet边界条件

2022-08-18韩沛东刘启新周子棋孙中国席光

西安交通大学学报 2022年8期

韩沛东,刘启新,周子棋,孙中国,席光

(西安交通大学能源与动力工程学院,710049,西安)

液滴或气泡的破裂与融合等自由表面流动是工业过程常见的流体动力学现象。由于自由表面常存在剧烈运动变形,传统基于网格剖分的模拟中多采用Level Set或VOF(volume of fluid)等数值方法,界面重构和尖角精确捕捉仍较复杂;基于拉格朗日框架的无网格粒子法避免了所有基于网格的限制[1]。光滑粒子流体动力学方法SPH(smoothed particle hydrodynamics)及移动粒子半隐式法MPS(moving particle semi-implicit method)等已广泛应用于计算大变形非定常流动[2-4]。在不可压流动计算中,与大气连通的自由表面粒子压力值常赋为0,可准确捕捉自由界面,但在负压梯度(即流体压力低于大气压,或界面法向压力梯度力朝向流体内部)算例中,自由表面粒子的核函数截断误差会影响方法的计算精度和稳定性[5],造成诸如粒子聚集、表面误判、压力求解误差增大等问题[6],是无网格粒子法研究的难点和热点之一。

国内外学者围绕算子修正、粒子分布重构、表面粒子判定、自由边界修正等方面开展了一系列改善研究。其中,Koshizuka等[7-8]采用粒子稳定项PST提升梯度算子稳定性;Liu等[9-10]提出用一阶、二阶修正矩阵提高算法在粒子分布不均匀时的精度。Khayyer等[11]基于粒子迁移技术PS(particle shifting)提出了优化的粒子迁移技术OPS(optizmized PS),通过粒子位置迁移调整(重构),显著提升了典型算例的收敛性;Jandaghian等[12]等提出了修正的粒子迁移技术CPS(corrected PS),与粒子碰撞模型结合,避免了粒子聚集并降低了数值噪声。Chen等[13-16]提出概念粒子模型,开发了无需自由表面粒子判定的MPS-NSD(no surface detection)方法,获得了进一步发展与应用;Khayyer等[11]提出了基于散度的表面粒子判定,提升了判定的准确性;朱跃等[17]提出了基于几何法和体积法的表面判定方式。Liu等[18-19]通过加入虚粒子修正自由表面及附近粒子梯度算子;Matsunaga等[20]通过移动的曲面网格来表示可变形的自由面边界,提升了计算精度;殷竞存等[21]采用改进的ghost粒子方法处理自由表面,获得较平滑的边界。上述工作对负压自由面流动的求解精度和收敛性起到一定提升作用。

然而,无网格粒子法通常对自由表面的狄利克雷边界条件(Dirichlet boundary condition)[1]直接赋值,将自由表面粒子所处位置即视为自由面边界,忽略了自由表面粒子不规则排布带来的空间离散误差。实际计算中,这一误差并不总能通过前述技术得到完全修正[22]。

方形液滴旋转算例[23]是检验负压条件下自由面大变形计算精度与稳定性的经典算例。相关研究大都聚焦高阶压力泊松方程和梯度、散度、拉普拉斯算子等方面,而本文利用该算例研究自由表面核截断区域计算精度。

本文提出了一种基于虚拟边界的狄利克雷边界条件,并在MPS框架下通过方形液滴旋转算例进行了验证,该方法可显著改善大变形复杂曲面的求解精度和稳定性。

1 数值方法

1.1 MPS方法

MPS方法[1]用于模拟不可压缩流动,在拉格朗日描述下,通过配点法实现空间离散。不可压缩流体的控制方程包括质量守恒方程与动量守恒方程

ρ·u=0

(1)

(2)

式中:ρ为流体密度;u为流体速度;p为压力;μ为动力黏度;f为体积力。

流体被表征为具有一定质量的离散粒子,粒子携带位置、速度、压力等物理量信息,通过粒子间相互作用,离散控制方程中的各项微分算子,导出梯度算子和拉普拉斯算子的光滑近似式。

MPS方法采用核函数模型描述粒子间作用,并凭此离散控制方程,本文采用如下核函数[6]

(3)

式中:w(r)为核函数值;r=|ri-rj|为两粒子i、j之间距离;re为光滑半径,其值为2.1倍粒子直径l0。

原始MPS方法中,负压会带来数值不稳定[23],通常将负压调整为零或更换更稳定的梯度公式[24]来实现仅有斥力的压力梯度计算。当计算存在负压与吸引力时,上述解决方式不再适用,因此本文采用带修正矩阵的梯度公式[23]

〈φ〉i=

(4)

式中:Cij为在引入的一个修正项,形式为一个矩阵的逆矩阵。在二维问题中,Cij可表示为

(5)

拉普拉斯算子计算公式为

(6)

式中:φ为任意标量函数;d为维度(二维d=2);n0为粒子数密度常数。在忽略连续域内核函数截断误差的情况下,拉普拉斯算子可简化为[9]

(7)

(8)

1.2 优化的粒子迁移技术

在使用上述模型时,粒子倾向于沿流线分散,会导致计算不稳定,常需采用OPS技术[11]来减小粒子分布的不均匀性。参考菲克第一定律,将高浓度粒子向低浓度粒子区域进行微小移动,即

(9)

(10)

式中:Cshift≤0.5为迁移系数;d0=l0;Ci为粒子分布浓度的梯度。

自由表面粒子以及邻近表面的内部粒子仅保留沿自由面切向的迁移分量为

(11)

(12)

(13)

粒子迁移后,凭借原流场参数更新速度场,即

ui′=ui+ui·δrii′

(14)

OPS技术使计算稳定性明显提升,但同时也导致表面粒子斥力失效[12],在计算含负压的自由面流动时,仍然会影响收敛性。

1.3 表面粒子判定

若要保证压力泊松方程计算结果准确,精确地判定自由表面粒子并施加Dirichlet边界条件至关重要。为保证表面粒子应判尽判,同时又避免內部粒子被误判为表面粒子,本文采用了多种判定方法组合的形式。

传统MPS方法[1]将粒子数密度小于αn0的粒子视为表面粒子,但常出现内部粒子误判为表面粒子的情况。将粒子位置矢量rij的散度·r作为评判标准[11],对于粒子均匀分布时的内部粒子该值为2。文献[16]提出虚拟光源和光幕的概念,将粒子i视为光源,邻近粒子视为遮挡物,将未遮挡面积占比Rill作为判定标准。

本文将上述方法相结合,对于粒子数密度小于0.99n0或·r<1.9的粒子进行光源遮挡判定,若Rill<1/6则视为表面粒子。若粒子数密度小于0.85n0或·r<1.5,则将该粒子强制判定为表面粒子。对于一个表面粒子,若其影响域内没有內部粒子,则将其视为游离粒子,不参与自由表面的计算。判定结果如图1所示。

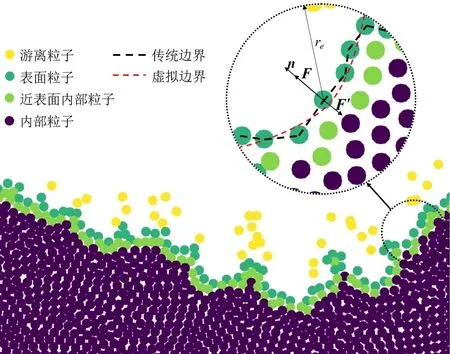
图1 自由表面附近粒子分布及虚拟边界示意图

2 虚拟边界

2.1 机理分析

传统MPS方法将自由表面粒子视为实际边界,并在施加狄利克雷边界条件时将其压力赋值为0,如图1所示。针对不可压缩流体,被自由表面粒子包裹的内部流体粒子的粒子数密度n保持恒定值n0,且在每个时间步粒子流动发生位移后,都会修正为n0。粒子间的相对位置决定了粒子间的相互作用,进而影响流动。

若自由表面粒子位置分布不够平滑,其用于描述实际自由面的形状便会出现误差,进而影响计算的精度和稳定性。单个自由表面粒子沿表面垂直方向发生偏移时,一般会产生以下两种情况。

(1)当压力梯度力朝向自由面外部时(如图1中F所示),若该粒子产生向外的偏移,压力梯度力减小,粒子之间斥力减小,该粒子向外偏移的趋势也会随之减小。反之,若该粒子产生向内的偏移,梯度力增大,粒子之间斥力增加,将遏制该粒子继续向内偏移。此时误差被自然修正,不会积累。

(2)当压力梯度力朝向自由面内部时(如图1中F′所示),若该粒子产生向外的偏移,压力梯度力减小,误差将逐渐扩大,该粒子会飘离自由表面,如图2(a)所示。反之,若粒子产生向内的偏移,粒子靠近,梯度力增大,可能导致局部高压无法抵消梯度力增大带来的吸引力,引起粒子继续向自由面内部挤压,产生非物理的局部高压,并最终导致计算发散,如图2(b)所示。

(a)粒子飘散 (b)局部高压失稳

2.2 方法原理

本文提出一种基于虚拟边界的狄利克雷边界条件赋值方法,其基本原理为在原计算的边界分布基础上构建表征真实表面边界的虚拟表面边界,通过计算表面粒子与虚拟边界的偏差量来对狄利克雷边界条件赋值进行修正。其中,实际的自由表面边界由表面粒子及其邻域搜索范围内的其他表面粒子连接而成,局部常为一条短曲线段,整个自由表面由许多这样的小曲线段联接组成。

每个短曲线段用二次曲线拟合,表面粒子位于拟合曲线上。自由表面的法向量与拟合曲线的对称轴重合,则拟合二次曲线y轴的朝向为该表面粒子的法向量方向。

2.3 算法流程

狄利克雷边界条件改进算法流程如图3所示。

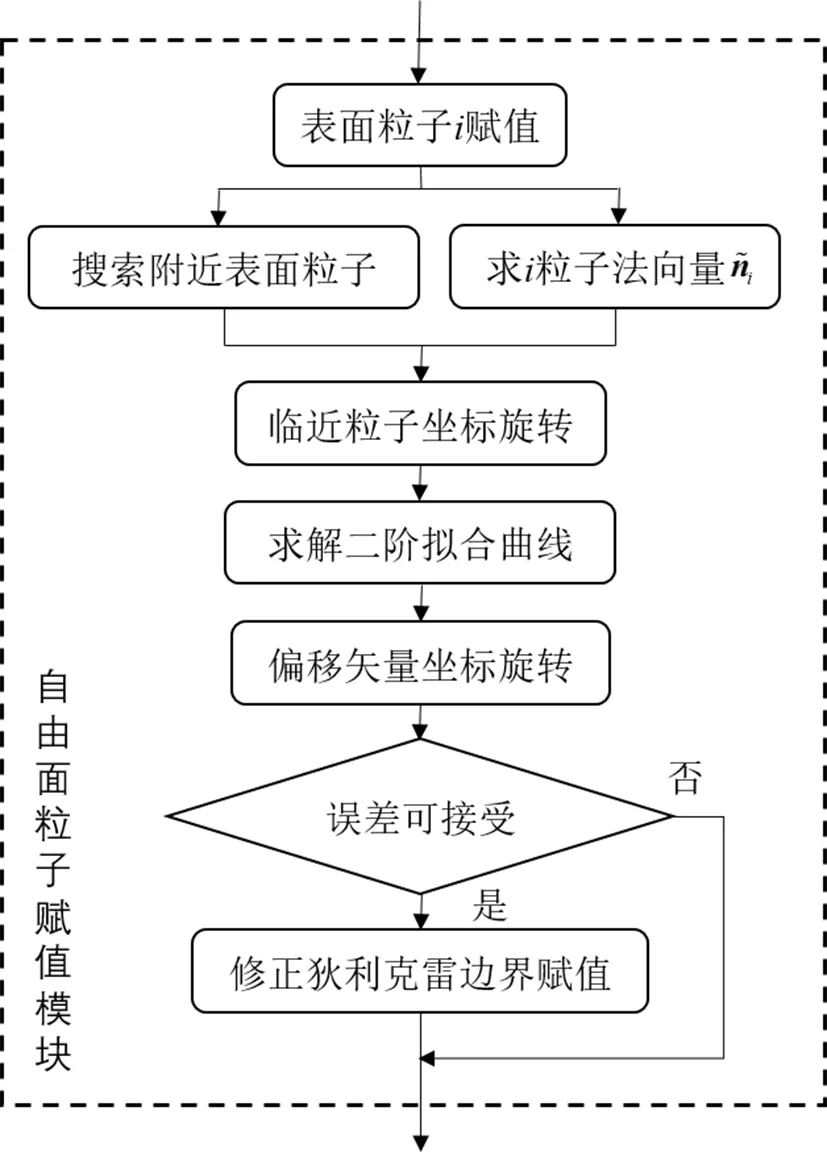
图3 狄利克雷边界条件改进算法流程

对于某自由表面粒子i,搜索其附近的其他自由表面粒子位置,同时计算i粒子的法向量,本文采用式(12)计算修正的法向量,采用坐标旋转公式

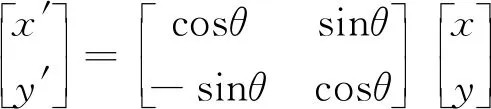
(15)

坐标旋转变换关系如图4所示,以i粒子为原点,对附近表面粒子进行坐标旋转,使y轴与法向量重合,θ为法向量与y轴的夹角。

图4 坐标旋转变换关系

粒子坐标旋转后,采用最小二乘法求解待拟合二次曲线的各项系数,并联立求解各项系数,即可得拟合二阶曲线方程

(16)

Q函数极值点对各项系数的导数为0,即

(17)

(18)

通过以上二阶多项式拟合,计算得到偏差最小的拟合曲线,即虚拟边界。凭借虚拟边界方程计算得出边界到该粒子的偏移矢量(0,b0)。并将偏移矢量沿-θ方向旋转回原始笛卡尔坐标,得到i粒子到虚拟边界的距离矢量δi。

最终,通过该表面粒子与此曲线的偏差和已求得的流场参数梯度进行插值计算,得出该表面粒子应当赋予的修正参数值

φi=φs+φi·δi

(19)

式中:φi为i粒子赋予的参数值;φs为狄利克雷边界条件预设的参数值;φi为i粒子处参数φ的梯度。

为保障二阶多项式的拟合精度,一般情况下,需要5～7个数据点。本文采用re≥2.5l0作为该模型搜索半径,邻近表面粒子与加上i粒子自身,满足上述拟合条件。

若出现i粒子附近的表面粒子分布与二次曲线分布差异较大的情况,可先对结果的方差进行校核,并在对狄利克雷边界条件赋值时,对b0的大小进行限制,令

b0=min(b0,δmax)

(20)

δmax取值影响自由表面粒子在虚拟边界附近松散分布程度,本研究中取值为0.6l0。实际模拟过程中可根据具体算例需求进行调整,推荐的取值范围为0.1l0～0.8l0。

此外,上述狄利克雷边界条件的赋值方法也可用于压力出口边界,采用改进的狄利克雷边界条件对表面粒子进行压力进行赋值

pi=ps+pi·δi

(21)

式中:ps为压力边界给出的压力值;pi可取i粒子的压力梯度或其上游2l0距离处的粒子的压力梯度。仅对距离压力出口一定范围内的表面粒子进行上述修正,可获得更平滑的压力分布。

将上述方法推广至三维时,需采用最小二乘法对粒子i附近的表面粒子进行曲面拟合,拟合二阶曲面时须采用的待定系数将由10个缩减至6个。

3 数值模拟验证

3.1 典型算例及设置

方形液滴旋转算例[12]是二维方形液滴在无粘和无表面张力的情况下以几何中心为转轴发生转动,在离心力作用下方块四角向外拉伸形成弯曲尖突,中心部分形成明显负压,四边发生显著内缩的剧烈形变过程。该算例中自由面平滑、尖突清晰、压力由外向内形成负压且成圆形等特征是检验负压计算和算法稳定性的经典算例。

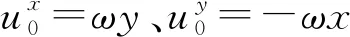
图5 方形液滴旋转算例

3.2 模拟结果

改进后方形液滴旋转算例压力云图及与文献结果比较如图6所示,其中方框为初始液滴位置,斜线为各角点的理论运行轨迹。图6(a)～(d)展示了0.5～2.0 s方形液滴的变形过程,与文献[18]中计算结果相比,形态和压力均吻合较好。但相比文献,使用伪粒子重整表面技术和更高精度的复杂模型,本文模型及实现过程更加简单快捷。

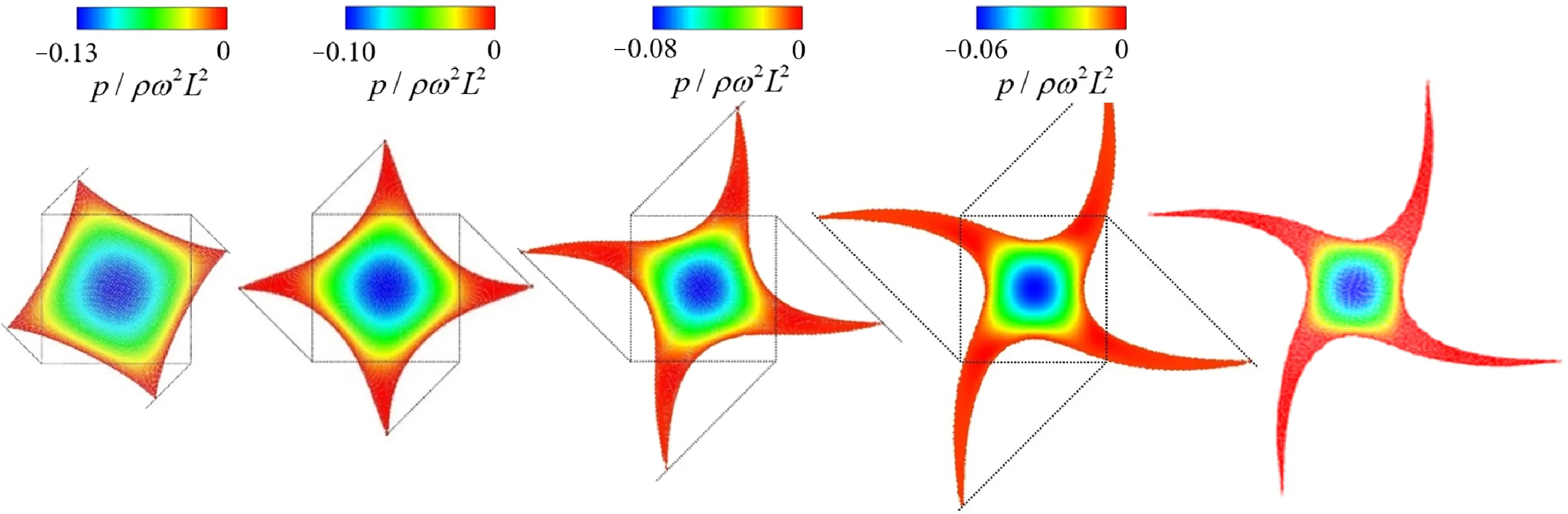
(a)t=0.5 s (b)t=1.0 s (c)t=1.5 s (d)t=2.0 s (e)文献结果

图7展示了添加修正矩阵和粒子迁移技术的方形液滴旋转计算结果,以及在此基础上添加了本文改进方法后的计算结果。结果表明,修正矩阵和改进的粒子迁移技术可在一定程度上避免拉伸失稳诱发的表面粒子聚集,但无法完全避免梯度力不足导致的粒子飘散问题。

采用本文提出的改进方法后(如图7(b)所示),表面粒子飘散现象得到明显抑制,液滴外形演变过程与理想结果相符,液滴内部的压力分布也变得更合理。t=2.0 s时,液滴中心压力为-54.53 Pa,换算为无量纲压力约为-0.055,与文献[11,18,22]计算结果相符。但四边内凹处边界曲线仍存在明显毛刺,考虑与粒子搜索半径选取相关。图7(c)展示了调整拟合曲线搜索半径由re=2.1l0增大为4l0后,曲线拟合数据由5～7个点进一步扩充至7～9个点,曲线拟合精度提升,边界毛刺现象基本消失。