含故障边的k元4立方体中的哈密尔顿性

2022-08-18田小润张建秀

太原科技大学学报 2022年4期

田小润，李晶，张建秀

(太原科技大学应用科学学院，太原 030024)

二十世纪电子计算机的出现，引发了信息科学突飞猛进的发展。近年来信息量的不断增加，在太空、国防、科技等各个领域中，迫切地要求计算机储存能力和运算速度的提升。因此，大规模并行计算机系统应用而生。大规模并行计算机系统中，互连网络在硬件成本、通信性能力、高效算法的潜力和容错能力方面起着至关重要的作用。近几十年来，有相当多的互连网络被提出作为大规模多处理器系统的底层拓扑。最流行互连网络之一是k元n立方体网络。k元n立方体网络具有许多理想的特性，比如易于实现、低延迟和高带宽的处理器间通信。因此，许多分布内存并行系统都是用k元n立方体网络构建的，形成底层拓扑结构，如IBMBlueGene[1]、J-machine[2]和CrayT3D[3].

1 预备知识

一个拓扑结构的互连网络用图G=(V(G)，E(G))来表示，其中V(G)代表图的顶点集，E(G)代表图的边集。经过图G中每个顶点仅一次的路(圈)，称为图G的哈密尔顿路(圈)，记为H路。若路的两个端点为s和t，则这条路可表示为(s，t)-路。如果一个图有哈密尔顿圈，则该图是哈密尔顿的。如果存在一条哈密尔顿路连接图中任意两个不同的顶点，则称图G是哈密尔顿连通的。二部图是指一个图G，它的顶点集可以分解为两个(非空)子集X和Y，使得每条边都有一个端点在X中，另一个端点在Y中。若点x在X中，点y在Y中，则称x、y在不同部。

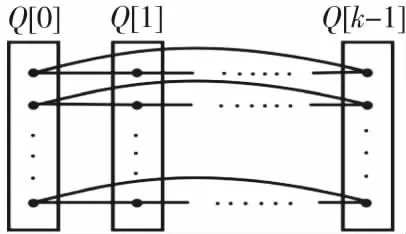
图1 划分为Q[0]，Q[1]，…Q[k-1]Fig.1 The division of Q[0]，Q[1]，…Q[k-1]

下面给出证明中需要用到的引理：

2 主要结论的证明

引理3在Q[i:j]中，设|F[i:j]|≤13，|Fp|≤7，且δ(Q[p]-Fp)≥2，其中p=i，i+1，…，j，则对Q[i:j]中任意两个不同部点s和t，当s，t∈Q[i]∪Q[j]时，Q[i:j]-F[i:j]中有(s，t)-H路。

证明：因为s，t∈Q[i]∪Q[j]，根据对称性，下面分两种情形讨论。

情形1s，t∈Q[i]

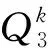
断言：路P上至少有一条可扩边可扩到Q[i+1].

因为|F[i:j]|≤13，最多有13条故障d维边。由于路P中包含k3-1条候选边，而每条故障d维边最多会使两条边不可扩。当k≥4时，k3-1≫2×13≥2×|F[i:j]|，所以断言成立。

设边(xi，yi)可扩到Q[i+1]，(xi+1，yi+1)是(xi，yi)在Q[i+1]上的对应边。由引理1，Q[i+1]-Fi+1中有(xi+1，yi+1)-H路P1.用路〈xi，xi+1，P1，yi+1，yi〉替换路P上的边(xi，yi)，可得到Q[i:i+1]上的(s，t)-H路。此时，在新哈密尔顿路上可找到可扩边，依此类推，最终得到Q[i:j]上的(s，t)-H路，如图2所示。

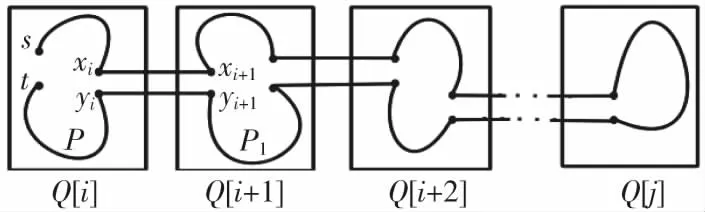
图 2 引理3 情形1Fig.2 Case 1 of lemma 3

情形2s∈Q[i]，t∈Q[j]

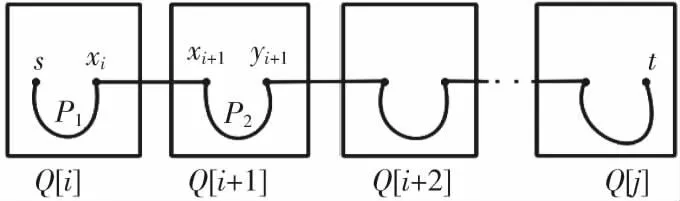
图3 引理3 情形2Fig.3 Case 2 of lemma 3

证毕。

引理4在Q[i:j]中，设S={s1，s2}、T={t1，t2}为不同部的顶点集。若|F|≤3，|F∩Ed|≤4，且S∪T⊂Q[i]∪Q[j]，则Q[i:j]有指定2-DPC.

证明：用数学归纳法证明。

当i=j，即Q[i:j]中只有1个子立方体时，根据引理2，结论成立。

假设Q[i:j]中有k-1(k≥2)个子立方体时，结论成立。

下面证明Q[i:j]中有k个子立方体时结论也成立。

情形1S∪T⊂Q[i]或S∪T⊂Q[j]

因为S∪T⊂Q[i]∪Q[j]，根据对称性，只证明S∪T⊂Q[i]的情形。

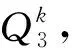
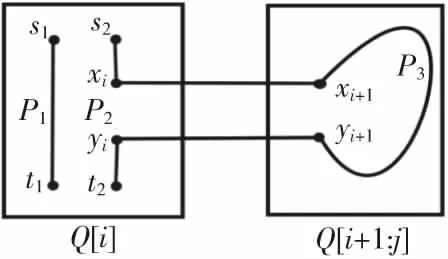
图4 引理4 情形1Fig.4 Case 1 of lemma 4

情形2{s1，s2，t1}⊂Q[i]，{t2}⊂Q[j]

如图5，在Q[i]中取一个与t1在同一部的可扩点xi，且xi可扩到Q[i+1]，设xi+1是xi在Q[i+1]中的对应点，显然xi+1与t2不在同一部。由引理2知，Q[i]-Fi中存在{P1，P3}是一个指定2-DPC，其中P1连接s1和t1，P2连接s2和xi.由引理3知，Q[i+1:j]-Fi+1:j中存在(xi+1，t2)-H路P3.令P4=〈s2，P2，xi，xi+1，P3，t2〉.此时{P1，P4}是Q[i:j]的一个指定2-DPC.因此结论成立。

图5 引理4 情形2Fig.5 Case 2 of lemma 4

情形3{s1，s2，}⊂Q[i]，{t1，t2}⊂Q[j]

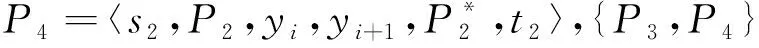
图6 引理4 情形3Fig.6 Case 3 of lemma 4

情形4{s1，t1，}⊂Q[i]，{s2，t2}⊂Q[j]

由引理1和引理3，在Q[i]中构造(s1，t1)-H路P1，Q[i+1:j]中构造(s2，t2)-H路P2即可。

情形5{s1，t2，}⊂Q[i]，{s2，t1}⊂Q[j]

此时，变换s2与t2的位置，则情况同情形3.证毕。

证明由引理1可知，当|F|≤11时，结论成立。故本文只需讨论|F|∈{12，13}时的情形。

情形1δ(Q[i]-Fi)≥2，i=0，1，2，…，k-1

不失一般性，设|F0|=max{|Fi|，i=0，1，2，…，k-1}，则|F0|≤9.

图7 定理1 情形1Fig.7 Case 1 of theorem 1

情形2子立方体中存在1度点

情形2.1Q[i]中仅有1个1度点

设该1度点为u，且u∈Q[0]，此时|F0|≥5且|F0∪F1∪…Fk-1|≤9.

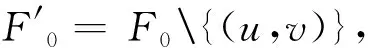
图8 定理1 情形2.1Fig.8 Case 2.1 of theorem 1

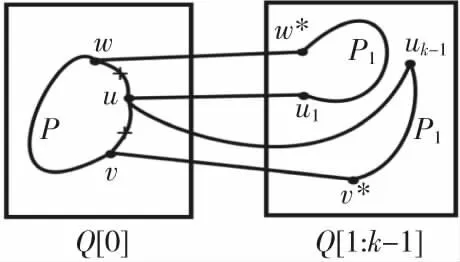
图9 定理1 情形2.1Fig.9 Case 2.1 of theorem 1

情形2.2Q[i]中存在2个1度点

设两个1度点分别用u、v来表示。此时点u、v必在同一个子立方中。如若点u∈Q[i]、v∈Q[j]中，情形如图10所示。因为点u、v均为1度点，沿维d划分后，子立方体与点u、v相邻的故障边数分别至少为5，即|Fi∪Fj|≥10，与|F1∪F2∪…Fk-1|≤9矛盾。故点u、v在同一子立方中，且为邻点。