基于关联系数定义下的证据合成新方法

赵法舜，马晓剑

(东北林业大学 理学院，哈尔滨 150040)

证据理论又称为Dempster-Shafer证据理论，由Dempster提出，Shafer进一步发展了该理论[1-2].作为一种不确定性多源信息融合方法，证据理论可以表达不确定信息，因而在不确定推理和多源数据融合中获得了广泛的应用[3-5].然而在实际问题中，证据理论的融合规则仅适合于解决高置信度、低冲突的情况，不能有效地处理信任度趋近于零或证据之间严重相悖的高度冲突情况，在这些情况下可能导致产生错误的融合结果.

为了解决高度冲突证据的融合问题，众多学者提出了很多改进方法，这些方法主要可以归结为两类:一类是修改Dempster组合规则[6-7]，主要解决冲突再分配问题；另一类是修改原始证据[8]，核心思路是修改原始证据后，再利用Dempster融合规则进行融合.

本文主要提出了一种关联系数定义下的冲突证据合成方法，通过修改原始证据对所有证据源进行预处理.基于概率转换，提出关联系数来衡量证据间的关联程度，该关联系数能够反映单元素子集和多元素子集之间的相互影响，并以此获得可信度权重；同时，利用信度熵考察每条证据的信息量大小，以确定赋予其信息量权重.联合关联系数与信度熵作为权重因子，根据Shafer提出的证据折扣思想，利用权重因子代替折扣系数对原始证据进行加权修正，最后利用Dempster融合规则完成融合.本文所提出的基于概率转换的关联系数可以很好地度量证据间的关联程度，给出的融合算法可以有效解决高度冲突问题，并优于其他经典算法.

1 D-S证据理论

Dempster-Shafer证据理论用于处理不确定信息，在没有先验信息的情况下可以进行多源证据的有效融合.当概率确定后，证据理论可以转化为贝叶斯理论，因此被认为是贝叶斯理论的扩展，但是证据理论需要的条件比贝叶斯概率理论更弱，适用范围更加广泛.基本概念介绍如下：

定义1.1(辨识框架)：

令Θ是由n个两两互斥元素组成的有限的完备集合，表示为:

Θ={A1,A2,…,Ai,…,An}

集合Θ被称为识别框架，A1,A2,…,An是辨识框架Θ的元素，Θ的幂集2Θ所构成的2n个元素的集合表示为：

2Θ={Ø,{A1},…,{An},{A1,A2},…,{A1,A2,…,Ai},…,Θ}

定义1.2(基本概率指派)：

对于辨别框架Θ，基本概率指派是从2Θ到[0,1]的映射m，形式为：

m∶2Θ→ [0,1]

其满足以下条件：m(Ø)=0，∑A∈2Θm(A)=1.

在Dempster-Shafer证据理论中，如果m(A)大于0，则将A称为辨别框架Θ上的焦元，基本概率指派后面简单记作BBA.

定义1.3(Dempster融合规则)：

在辨识框架Θ上，设有n个BBA为m1,m2,…,mn，并假设这n个BBA是相互独立的，则由m=m1⊕m2⊕…mn表示的Dempster融合规则称为正交和，定义如下：

(1)

其中：K=∑(A1∩A2∩…∩An≠Ø)m1(A1)m2(A2)…mn(An)称作冲突系数，表示BBA之间的冲突，且Dempster的融合规则适用于冲突系数K<1的情况.

定义1.4(Pignistic概率转换[9])：

假设m是辨识框架Θ下的BBA，通过概率转换可以转变为概率测度BetP:

(2)

其中:|B|表示B的基数.

定义1.5(相似系数)：

王肖霞[10]在Dempster融合规则的基础上引入了相似系数的概念，用来衡量证据间置信度分布的相似程度，证据mi和mj之间的相似系数定义为：

i,j=1,2,…,n

(3)

其中：Ax和Ay分别表示证据mi和mj的焦元.

2 关联系数定义下的证据合成方法

为降低高度冲突发生的可能性，本文算法选取修改原始证据的方法，对证据源进行预处理，首先利用关联系数来衡量证据间的关联程度；同时利用信度熵考察每条证据的信息量大小，联合关联系数与信度熵作为权重因子，对证据源进行加权修正，再将得到的结果利用Dempster融合规则自身融合(n-1)次，完成多源证据间的合成.

2.1 基于概率转换的关联系数

相似系数可以度量证据之间的相似程度，但将多元素子集作为单元素子集进行计算，忽略了多元素子集对证据间相似程度的影响，以下给出反例：给定三个BBA分别为m1、m2和m3，辨识框架Θ={A,B}，它们的置信度分布如下：

m1∶m1(A)=0.6;m1(B)=0.2;m1(A,B)=0.2

m2∶m2(A)=0.2;m2(B)=0.6;m2(A,B)=0.2

m3∶m3(A)=0.2;m3(B)=0.2;m3(A,B)=0.6

由式(3)可以得到，m1与m2及m3的相似系数相同，即SIM(m1,m2)=SIM(m1,m3)=SIM(m2,m3)=0.636 4.显然，m1与m2及m3之间互有差异，且m1与m2的相似度要小于m1与m3的相似度.然而，相似系数计算的结果表明，m1与m2及m3之间没有差异，这显然违背常识.因此，为了解决上述问题，本文提出了关联系数来衡量证据间的关联程度.由定义1.4可知，Pignistic概率变换保持单元素子集的置信度不变，并将多子集的置信度均匀分配给所包含的单子集.受此启发考虑利用每个单子集焦元的BetP来代替BBA进行计算，关联系数既可以充分反映单子集和多子集之间的相互作用，又有效避免了相似系数将多子集视为单子集的情况.另外，当BBA仅由单子集组成时，关联系数与相似系数完全一致.

定义2.1(证据向量)：

假设Θ= {A1,A2,…,Ai,…,An}，存在证据集合E={E1,E2,…,Ei,…,En}，对应的BBA分别为m1,m2,…,mi,…,mn,证据向量表示为：

Ei=(BetPmi(A1),BetPmi(A2),…,BetPmi(An))T,i=1,2,…,n

定义2.2(关联系数)：

关联系数用来度量证据间的关联程度，定义如下：

SBetP(mi,mj)=〈Ei,Ej〉=

i,j=1,2,…,n

(4)

定理1：关联系数可满足以下性质：

1)SBetP(mi,mj)=SBetP(mj,mi)

2) 0≤SBetP(mi,mj)≤1

3)若mi=mj，则SBetP(mi,mj)=1

证明：

1) 由分子项均为实数可知，

SBetP(mi,mj)=

SBetP(mj,mi)，故满足交换律.

2)显然SBetP(mi,mj)为大于等于0的实数，当且仅当Ax∩Ay=Ø时，SBetP(mi,mj)=0，由柯西-施瓦茨不等式：

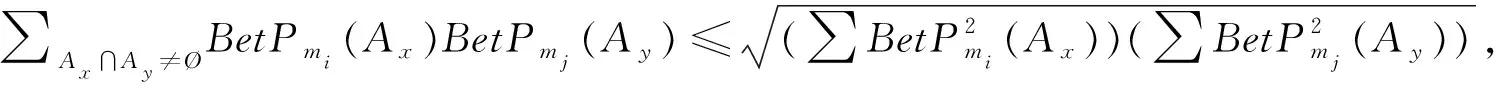
3)mi(Ax)=mj(Ay)⟹BetPmi(Ax)=BetPmj(Ay)，由式(2)的证明可知，SBetP(mi,mj)=1.

证毕.

例1：假设Θ={A,B},两个BBAm1和m2表示为：

m1:m1({A})=x，m1({B})=1-x
m2:m2({A})=1-x，m2({B})=x

图1描绘了x在[0,1]变化范围内SBetP(mi,mj)变化的曲线，Δx=0.02.由图1可以看出，当x取0或1时关联系数为0，表示证据完全相悖；当x取0.5时关联系数为1，表示证据完全相同；且越接近于中值0.5时关联系数越大，即关联程度越高，符合现实规律.另外，在本例中再次验证了关联系数满足对称性和非负性等基本性质.

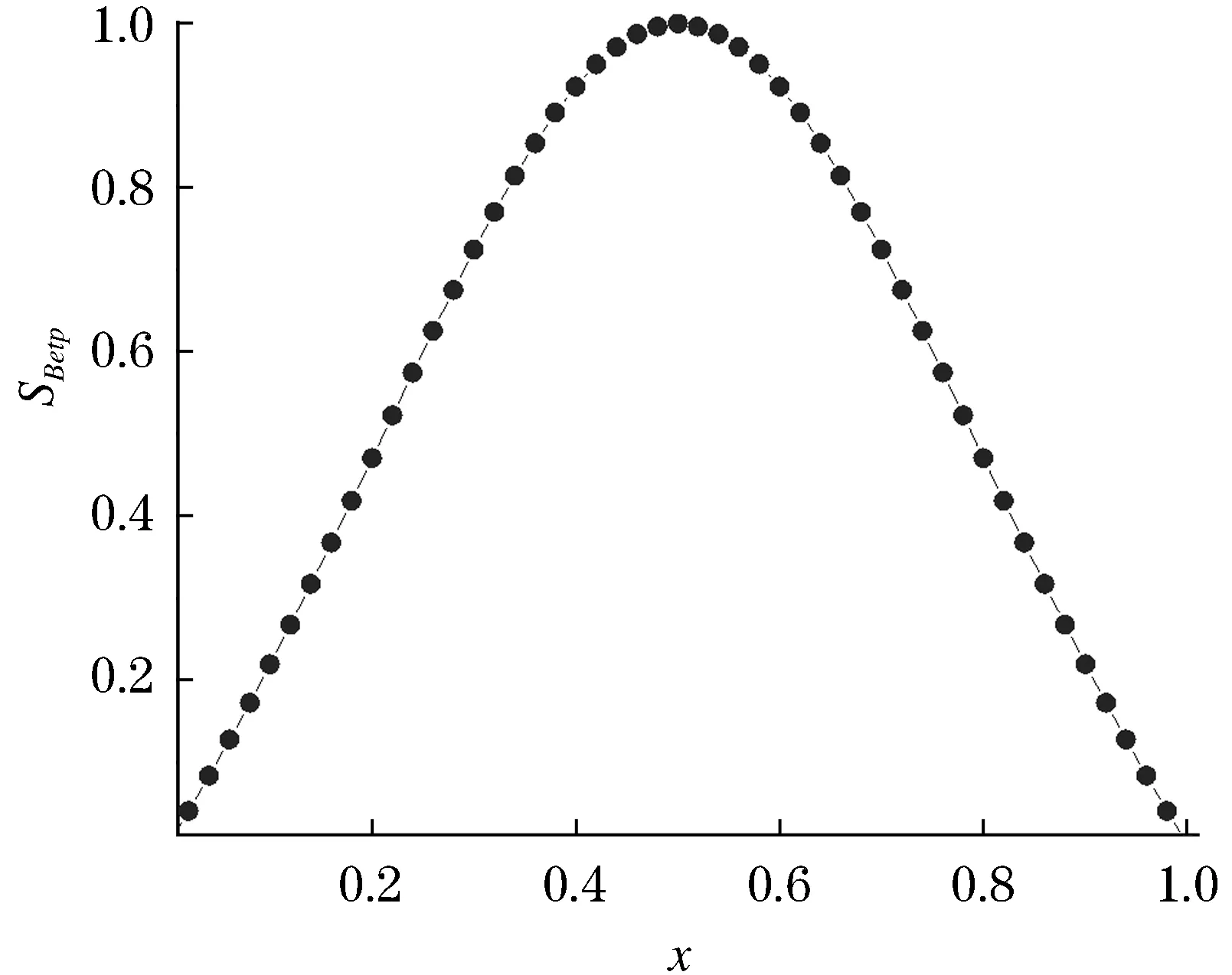
图1 关联系数随x的变化Figure 1 The coefficient of correlation varies with x

例2：假设有两个BBAm1和m2，置信度分布如下所示.辨识框架Θ={A,B,C,D,E,F,G,H}，α从0以Δ=0.1的速度增加到1，子集的基数T从1变为8，如表1所示.

m1∶m1 (B)=α，m1 (T)=1-αm2∶m2 (B)=0.9，m2 (T)=0.1

关联系数随|T|及α的变化如图2所示，可以看出，无论变量|T|及α如何变化，关联系数在0～1之间波动，这验证了关联系数的有界性，其范围取值为[0,1].当|T|=1时，证据m1和m2由单子集组成，子集之间没有交集，因此关联系数小于其他|T|值的关联系数.当|T|从2增加到8时，关联系数相应减小，这是因为多子集的基数扩展使不确定性增加.图2(B)所展示的是当|T|固定时，关联系数随着α的增加而增加，这符合直观判断，因为两个BBA的置信度分布越来越相似.

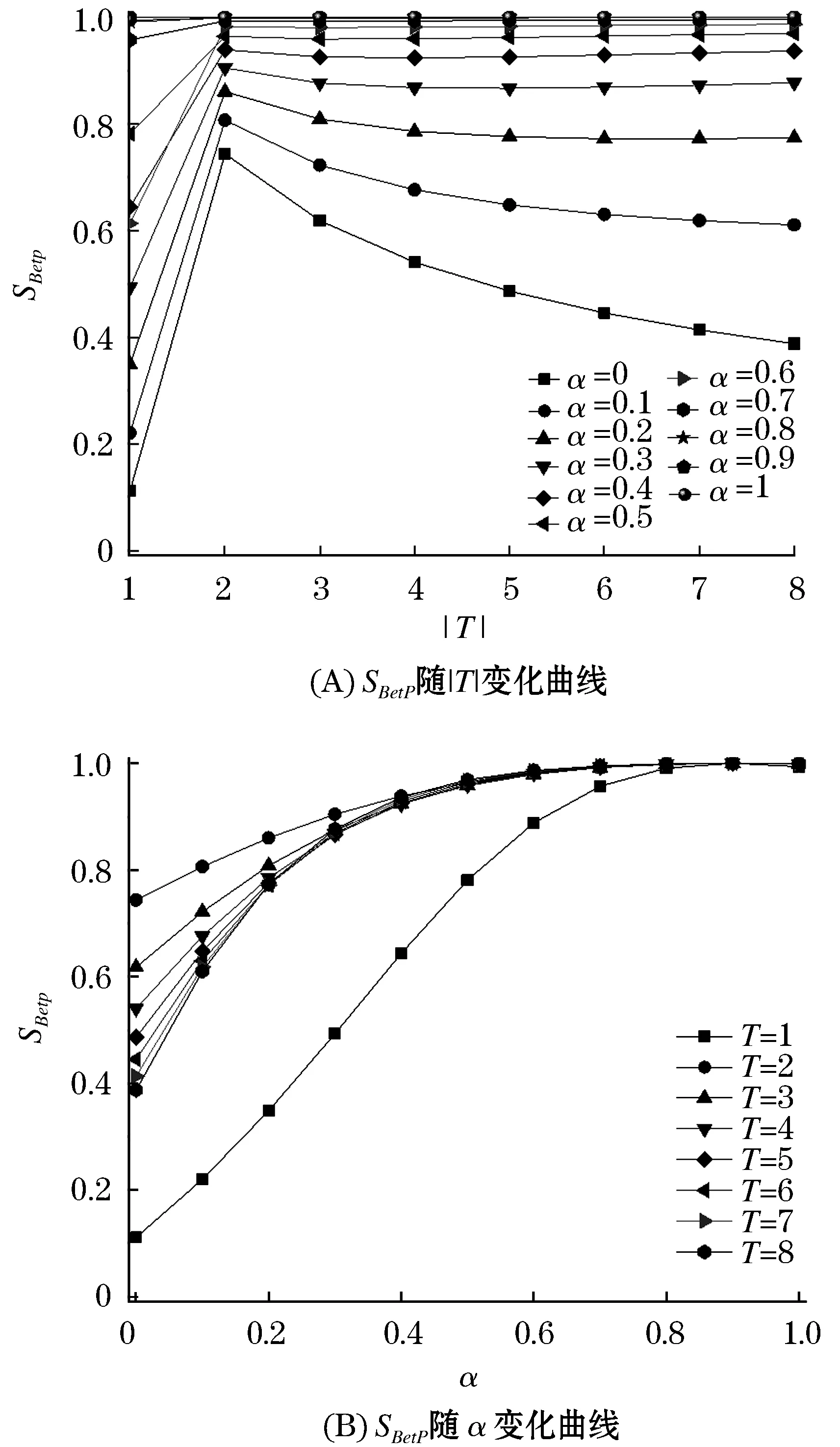
图2 例2中SBetP(mi,mj)随α & |T|的变化曲线Figure 2 The change of SBetP(mi,mj) with α & |T| in example 2

2.2 证据合成新方法

关联系数SBetP(mi,mj)可以反映证据mi和mj之间的关联程度，证据间的置信度分布差别越小，对应的关联系数越高，被其他证据支持的程度越高.为了便于表达，本文使用Sij替代SBetP(mi,mj).通过以上公式得到关联系数矩阵SM，表示为：

计算每条证据的支持度定义如下：

(5)

将每个证据的支持度归一化处理作为可信度权重，可信度表示为：

(6)

同时，邓勇[11]提出了信度熵，作为香农熵的推广，信度熵是测量不确定信息的有效方法，它可以应用于证据理论中，其中不确定信息用BBA表示.令Ai为BBA的焦元，|Ai|是集合Ai的基数，Ai的信度熵Ed定义如下：

(7)

当仅将BBA分配给单个元素时，信度熵退化为香农熵，即：

(8)

信度熵可以表示证据信息量的大小，当涉及证据间的信息增多时，熵会增加.在图2中信度熵随集合元素个数的增加而增加，说明信度熵越大，它应该得到其他证据更多的支持.此外，为了避免在某些情况下给证据分配零权重，使用信息量ICi来测量证据的信息量大小，取对数使得信息量与信度熵成正比.Ai的信息量为：

(9)

综上实现了两个权重因子的提取，修改证据完成证据预处理过程的伪代码如下：

-------------------------------------------

算法:基于关联系数定义下的证据合成方法

-------------------------------------------

输入:输入原始证据

1)计算n个证据的关联系数矩阵SMij,1≤i≤n,1≤j≤n.

2)计算证据可信度Rei，i=1,2,…,n.

3)由信度熵计算证据的信息量ICi，i=1,2,…,n.

6)将预处理的结果利用证据理论的融合规则，自融合(n-1)次得到最终结果.

输出:新的证据

-------------------------------------------

2.3 合成方法的算例分析

为了验证该方法的有效性，本文给出了一个诊断应用，现有三条证据如表2所示.其中Θ={A,B,C}，m(A)、m(B)和m(C)分别表示A、B、C的BBA.

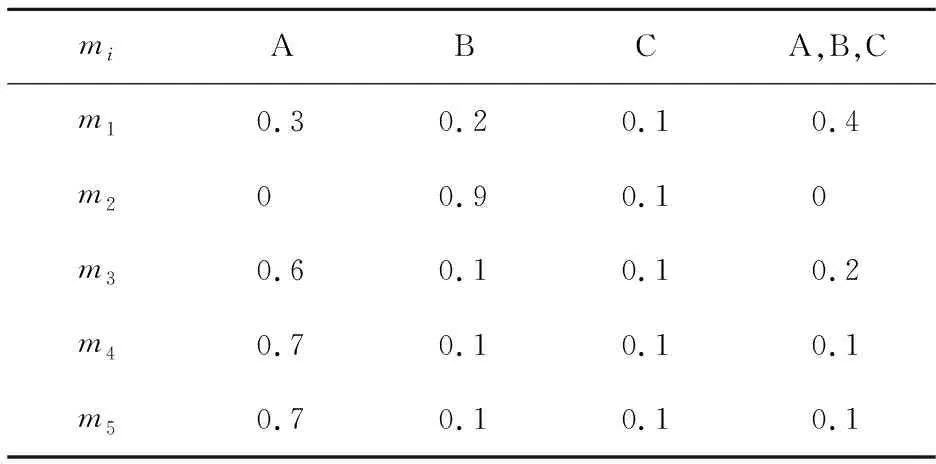
表2 原始证据BBA

根据伪代码的算法流程，可以得到本文算法的融合结果，并与其他经典算法比较如表3所示.

表3 仿真算例结果比较

根据多源证据的融合结果，本文算法可以诊断A具有最大的置信度，符合直观判断.然而，Dempster的组合规则方法不能很好地处理冲突证据，常常得出错误的结果，即诊断为B.此外，Murphy等人的方法虽然可以正确识别对象，但没有考虑证据间的关联性，导致有效识别目标的速度较慢；邓勇的方法在多源证据诊断下可以保证准确率，但决策源较少时容易产生误判，稳定性低于本文算法.同时，随着更多证据源的加入，融合信息增多，支持诊断为A的置信度也发生改变.从图3可以看出，当融合的证据源只有两个时，关联系数为两个BBA分配相同的支持度，所以置信度较低是合理的.当证据源增多时，诊断为A的置信度不断增加，通过与其他算法不同数量证据源融合结果的比较，说明在有证据冲突的情况下，本文算法具有更为有效的融合结果.

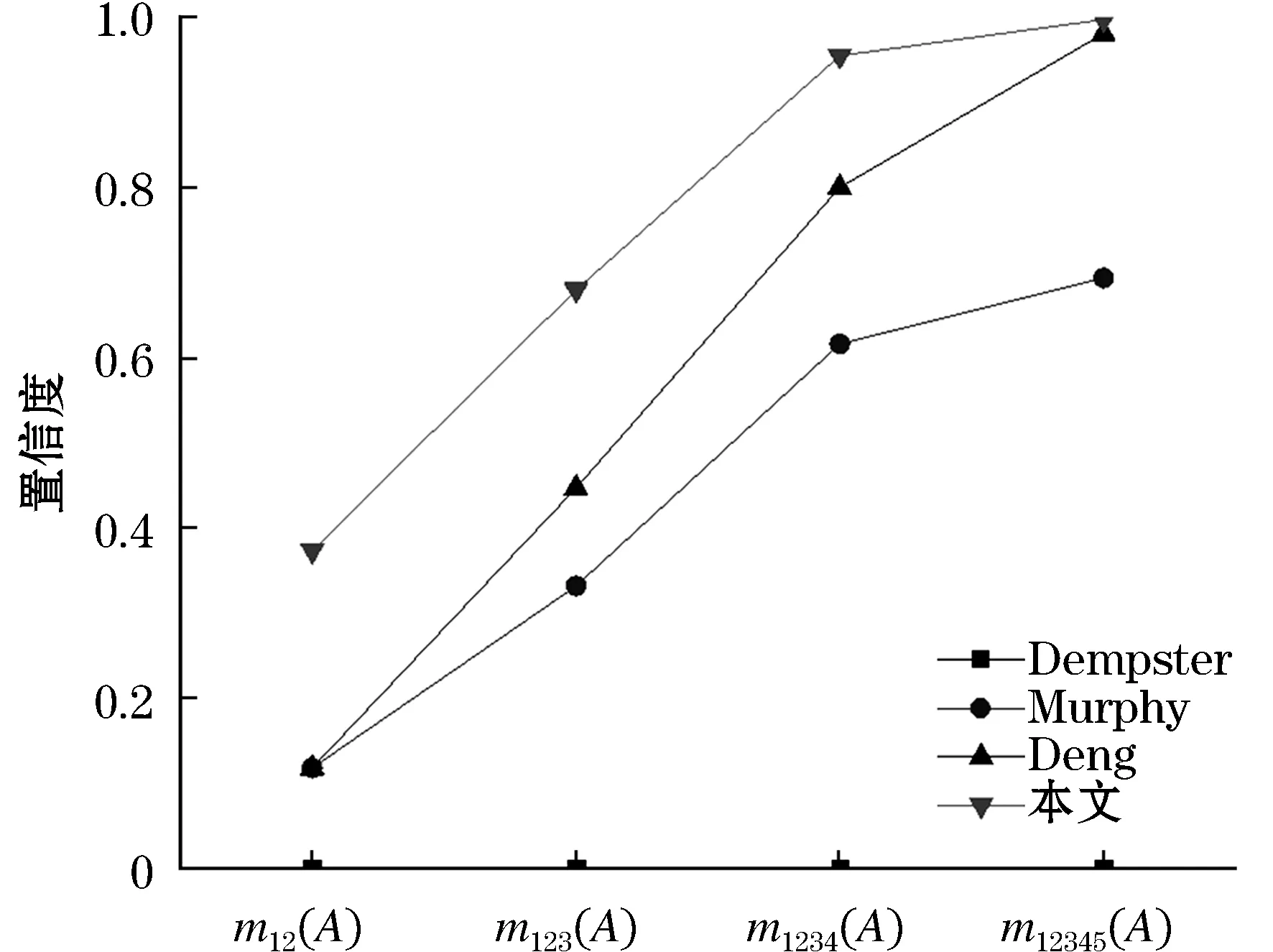
图3 不同数量证据源融合的置信度比较Figure 3 Comparison of confidence in fusion of different number of evidence sources

3 结 语

本文提出了一种新的证据间关联程度的度量—关联系数，它加入了概率转换的元素，能够反映不同子集之间的相关性，并具有有界性、非负性和对称性等良好性质. 本文提出的基于关联系数定义下的多源证据融合方法，为了充分反映证据之间的关系，利用证据的可信度权重和信息量权重来确定证据的权重因子，并通过具体算例说明了算法的有效性.该证据合成方法不仅可以有效实现多源证据的合成，而且提高了证据冲突时融合结果的可靠性和合理性.在未来的研究中，将进一步利用关联系数和证据融合方法在更多实际应用中实现有效决策.