多用户多边缘的公平卸载及优化策略研究
2022-08-18赵梦远郝万明杨守义
赵梦远, 郝万明, 杨守义, 王 芳,2,3
(1.郑州大学 信息工程学院 河南 郑州 450001;2.郑州大学 电子材料与系统国家级国际联合研究中心 河南 郑州 450001;3.郑州大学 河南省电子材料与系统国际联合实验室 河南 郑州 450001)
0 引言
随着物联网技术的快速发展,智能应用急速增加,例如互联网游戏、智能医疗[1-2]、智能车载网络[3]以及虚拟现实[4]等。这通常需要设备执行计算密集型和时延敏感[5-6]的任务,为确保任务高效计算,边缘云计算(mobile edge computing, MEC)、雾计算和设备对设备(device-to-device,D2D)应运而生[7-9]。其中MEC通过在物联网边缘提供计算资源,为资源受限的物联网设备提供计算[10]。计算卸载是MEC的关键技术,通过将任务从资源受限的设备卸载到边缘服务器,减少设备执行延迟和能耗。
现阶段对边缘计算的研究已有丰富的成果,从卸载方式大体上分为:1)考虑粗粒度卸载,整体卸载到云上或在本地执行,如文献[11]在多用户情况下应用博弈论研究分布式卸载策略,实现能耗和时延的优化。2)考虑细粒度卸载,文献[12]考虑单用户多线程,在云和边缘云协作中开发了一个细粒度的多线程计算卸载策略来解决线程选择、协作以及卸载决策等问题。文献[13]在多用户物联网设备场景下提出了一种基于云-MEC协同任务卸载方案。对任务卸载的计算消耗、通信消耗和延迟进行建模,并针对具有不同资源需求和延迟敏感性的任务实现差异化的卸载决策。文献[14]将应用分为有向无环(direct acyclic graph,DAG)的子任务,提出了一种有效的多用户边缘系统卸载方案,将物联网任务卸载到最适合的边缘服务器,从而使预期的执行时间最小。现有成果大部分都聚焦在时延和能耗的优化,但对于设备时延的公平性研究较少。文献[15]考虑到用户的公平性,在多用户情况下,将任务视为可随意划分的子任务,将计算卸载问题表述为最小-最大问题,使得所有用户间的最大任务执行时间最小。以上研究都没有在子任务相互依赖的场景下,考虑多个用户在多个边缘云的公平卸载。
在多个边缘服务器的场景下,将物联网设备的任务分成可依赖的DAG子任务,研究其卸载策略,对物联网设备实现低时延和公平性的折中。本文基于已有算法优化整体时延的同时,考虑最小化最大完成时间,为解决这一问题,提出了一种基于潜在博弈论的分布式卸载策略。首先构建一个效应函数最大化问题,将此效应函数最大化表述为策略博弈。而后通过潜在博弈论证明此策略博弈是潜在博弈。最后,经过有限次迭代达到纳什均衡,求得最初问题的次优解。
1 系统模型
假设有n个物联网设备,N={1,2,…,i,…,n},每个物联网设备包括一组子任务Ve=(1,2,…,j,…,ve)。m个边缘服务器,M={1,2,…,k,…m}。利用G=(V,e)来描述这些任务之间的依赖关系,其中:V是子任务的集合,每个子任务在执行过程中不可中断;e是表征子任务之间依赖关系的一组有向边,例如,有向边(vi,vj)意味着任务vj依赖于结果任务vi。
先由代码分析器判断可以卸载到边缘服务器的子任务,其余子任务必须在本地执行,再由系统分析器监控参数,例如无线带宽、要上传的数据大小以及执行或传输各种子任务所花费的能量,最后,确定子任务是否卸载。在设备能耗允许情况下,考虑优化时延的同时,实现用户公平性卸载,更多分析用户的体验质量(quality of experience,QoE)。
1.1 通信模型
考虑多用户多边缘服务器,对于物联网设备i的第j个子任务,即Ti,j,用Ti,j=(di,j,ci,j,ai,j)来表示。其中:di,j表示计算输入数据的大小;ci,j表示完成任务所需的总CPU周期;ai,j={0}∪M表示物联网设备i的第j个计算子任务的卸载决策。ai,j=0,表示设备i的第j个子任务在本地执行,ai,j=k,∀k∈M表示Ti,j被卸载到第k个边缘设备上。
1.2 信道模型
根据瑞利衰落信道模型,传输速率表示为

1.3 计算模型

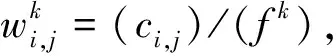

式中:σi为输出数据大小与输入数据大小的比率。
1.4 任务模型
子任务j′必须在任务j完成后才可以开始执行,设备任务的首尾必须在本地执行,最后一个子任务负责处理执行结果,即子任务的结束时间和整个任务的结束时间分别表示为
2 问题模型
本文在最小化用户整体时延的同时考虑公平性卸载。首先分配子任务到合适的服务器优化单个用户的时延,然后在多用户情况下最小化最大设备任务完成时间。由于多用户在多个边缘云间的任务卸载,导致用户完成时间产生差值,文中用max(Ti)和min(Ti)的差值衡量用户公平性卸载。最小化所用公式为
(1)
(2)
s.t. C1:Costi≤B,∀i∈N,
(3)
(4)
C2:ai,j=0∪M,
其中:约束条件C1为能耗约束,如用户选择在边缘计算,则边缘计算的能耗不应大于设备规定的能耗;约束条件C2表示子任务可以选择在本地或者任一边缘服务器执行;约束条件C3表示一个子任务只能连接在一个边缘服务器或选择在本地执行;Costi是边缘计算的能耗;B是设备规定的能耗。
3 最小最大化公平卸载策略
在单用户MEC环境中,关键是解决子任务的卸载,通过找出设备任务的关键路径,来获得子任务的优先级,关键路径越长,子任务优先级越高,按照优先级高低对子任务调度,选择是在本地计算还是卸载到边缘服务器,目的是尽可能降低时延[15]。再考虑多用户MEC环境中,为实现多个物联网设备的公平卸载及时延优化,构建设备i的效应函数为
式中:Top为定义的每个设备完成时间的理论最优值。
根据上述系统模型,单用户卸载策略完成后,在多用户多MEC环境中,为优化问题(3)和(4),文中提出效应函数最大化卸载算法(effect-function maximization offloading algorithm,EFMO),该算法将上述优化问题转化为策略博弈,该策略模型表示为Г=(N,{Ai}i∈N,{Ci}i∈N),Ai=(a1,a2,…,ai,…,an),其中:an包括每个子任务的卸载决策ai=(ai,1,ai,2,…,ai,j,…,ai,ve)。将最小化最大任务完成时间问题转化为最大化效应函数问题,即
3.1 潜在博弈

构建一个势函数公式为
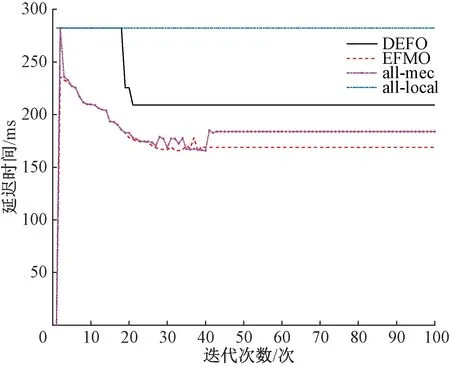
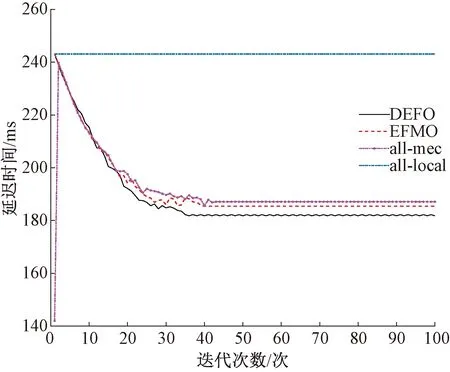
当设备i的策略由ai=0更新为a′i=k时,即Ci(ai,a-i) 同理证明其他两种情况ai=k更新为a′i=0;ai=k更新为ai=k′。可以得出随着效应函数的增加,势函数也增加,证明该策略博弈是一个潜在博弈,当物联网设备i存在策略a′i,使得Ci(a′i,a-i)>Ci(ai,a-i),则物联网设备i需要更新其策略ai。 基于潜在博弈论的EFMO算法解决优化问题的伪代码如下。 输出:优化整体时延并最小化最大任务完成时间的卸载策略。 用户的策略集Ai=(a1,a2,…,ai,…,an),其中ai,j∈{0,1,2,…,m}; 初始化,用户i的卸载策略ai,1,ai,2,…,ai,j…ai,ve=0; for 每个时隙t for 所有i∈N for 所有k∈M for 设备i的子任务 子任务j在本地执行; else 在服务器k执行; 只对效应值最大的函数投票卸载并广播给其他所有用户; if 设备i获得更新机会 C′i>Ci; ai更新卸载决策改成a′i; else 没有用户获得更新机会; 获得每个用户的最优卸载方案及其子任务调度,实现多用户的公平性卸载。 文章中用设备的最大完成时间和最小完成时间的差值衡量用户公平性,实现最小化最大任务完成时间。在多用户的情况下,通过引入潜在博弈的定义,并设计了一个分布式计算卸载算法。仿真参数的设定如表1所示。 表1 仿真参数的设定 如图1~2所示,本文提出的算法EFMO、设备的子任务全部在本地运行的算法(all-local)、全部在边缘云(all-mec)和分布式最小用时卸载算法(distributed earliest finish-time offloading algorithm,DEFO)[14]在5个边缘服务器下进行比较。 图1 DEFO、EFMO、all-mec和all-local算法任务完成时间差值对比 图2 DEFO、EFMO、all-mec和all-local算法任务完成平均时间对比 EFMO算法是基于博弈论的算法,经过有限次迭代达到纳什均衡。通过图1、2,可以得出EFMO算法相较于DEFO、all-local、all-mec算法,在公平性卸载上有明显改善。EMFO算法在卸载时同时考虑单个用户时延最优和最小化最大用户任务完成时延,相比只考虑优化单个用户时延的DEFO算法差值缩短了40 ms,并且优于非云边协同的all-local算法和all-mec算法;平均值和DEFO算法差别较小,约在3 ms。图3为EFMO算法和DEFO算法在相同用户规模下,服务器数目从1增加到10任务完成时间的差值对比情况。图4为两种算法在相同数目的边缘服务器下用户规模的增加,通过大量仿真实验得出,EFMO算法一直优于DEFO算法。EFMO算法的纳什均衡收敛点随着用户规模的增加,增长速度逐渐变慢。 图3 DEFO和EFMO算法任务在不同服务器下完成时间差值的对比图 图4 DEFO和EFMO算法任务在不同用户数完成时间差值的对比图 如图5所示为EFMO算法和多设备多服务器系统的整体卸载的基于潜在博弈卸载算法(potential game based offloading algorithm,PGOA)[11]平均时延的比较,随着用户规模从2增加到25,在相同边缘服务器的情况下,用户总体的时延明显优于PGOA。图6所示为EFMO算法在细粒度和公平性的卸载情况下,随着用户规模的增加,相较于粗粒度的卸载PGOA算法有更多机会卸载到边缘云上。 图5 EFMO算法和PGOA算法在不同物联网设备下平均时延的对比 图6 EFMO算法和PGOA用户卸载数目 本文提出了一种基于博弈论的分布式卸载算法,解决多用户在多个MEC系统中的时延优化和公平性卸载,将用户的任务分为相互依赖的子任务,实现了时延整体优化并最小化最大完成时间。本文证明了该策略为潜在博弈,并存在纳什均衡点,大量仿真实验证明了该算法较之前算法在公平性上有明显提升。接下来将扩展应用场景,考虑设备到设备通信,将资源卸载到附近空闲设备,进一步优化时延,缓解单个设备的资源稀缺,提高边缘的整体资源利用率。3.2 纳什均衡
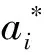
3.3 算法描述


4 仿真与结果分析





5 结论
