平行纺成纱质量指标回归分析及工艺参数优化

冯清国 任家智 陈宇恒 叶 静

（中原工学院，河南郑州，450007）

近些年来花式纱线以广泛的原料适用性、丰富的色彩、变化的外观效果极大程度地丰富了产品的花色品种［1］。而平行纱作为花式纱的一小分支，因其独特的包缠结构，纺制的纱线具有表面毛羽少、纱体柔软、蓬松性好、条干好、强力高等优点，受到了越来越多学者及研究人员的关注［2-3］。

文献［4-5］根据不同的外包纱和芯纱组合对平行纺的形式及特点进行了研究，文献［6-7］丰富了平行纺的适纺原料组成，弥补了各自纤维成纱的缺陷。文献［8-9］对长丝包缠数和纱线强力的关系进行了研究，认为纱线强力随长丝号数的增加而增加，但成本会大幅度增加。文献［10］认为包缠张力的大小会影响平行纱的强力与断裂伸长率。包缠张力增大，纱线强力增加，伸长率下降；包缠张力增加到一定程度，强力不再增加或增加很少，伸长率也趋于平稳。文献［11］通过对包缠纺结构及性能的分析，提出了对平行纺的工艺创新优化。

对平行纺来说［12］，包缠捻度和包缠张力是影响平行纱纺制的重要工艺参数［13］，直接影响纱线的外观质量及内在结构。本研究利用响应曲面法对平行纺纱工艺进行优化设计，以期获得最佳工艺并对生产实践具有一定的指导作用。

1 试验方案

1.1 试验原料及纱线规格

以棉/锦纶88/12 粗纱（定量5.34 g/10 m）为芯纱，涤纶长丝5.56 tex 为外包纱，纺制线密度为26 tex+5.56 tex 的平行纱。

1.2 试验工艺参数设置

采用HFX-07 型花式捻线机，主要工艺参数：空心锭转速5 000 r/min ，输出罗拉线速度2 m/min，总牵伸20.56 倍，后区牵伸1.5 倍，包缠张 力0.9 倍～1.0 倍，包 缠 捻 度500 捻/m～800 捻/m，牵伸罗拉直径25 mm×25 mm×25 mm，罗拉中心距52 mm×46 mm ，输出罗拉直径42 mm，引纱罗拉直径82 mm，钳口隔距3 mm，摇架压力140 N/双锭。

1.3 性能测试指标及测试条件

采用YG061 型单纱强力仪测试纱线断裂强力。测试长度250 mm，拉伸速度250 mm/min，测试10 次并取平均值。采用USTER ME100 型条干均匀度仪测试条干CV。测试速度200 m/min，测试时间1 min，测试10 次并取平均值。测试环境相对湿度（65±5）%，温度（20±2）℃。

1.4 试验方案及结果

由于包缠捻度和包缠张力是平行纺的重要工艺参数，直接影响纱线的外观质量及内在结构，因此利用Design Expert 软件，采用Central Composite Design（CCD）设计响应曲面，对包缠捻度和包缠张力进行优化，以期获得最优纺纱工艺。 在CCD 设计时，只要给出各个试验因子试验条件取值的上下限范围，软件将自动对处理水平进行编码，即Zj=（xj-xj0）/Δj，式中：Zj为规范变量，xj为自变量，xj0分别为自变量的零水平，Δj为变化区间［14］。因子水平编码表如表1 所示，试验设计方案及指标测试结果如表2 所示。

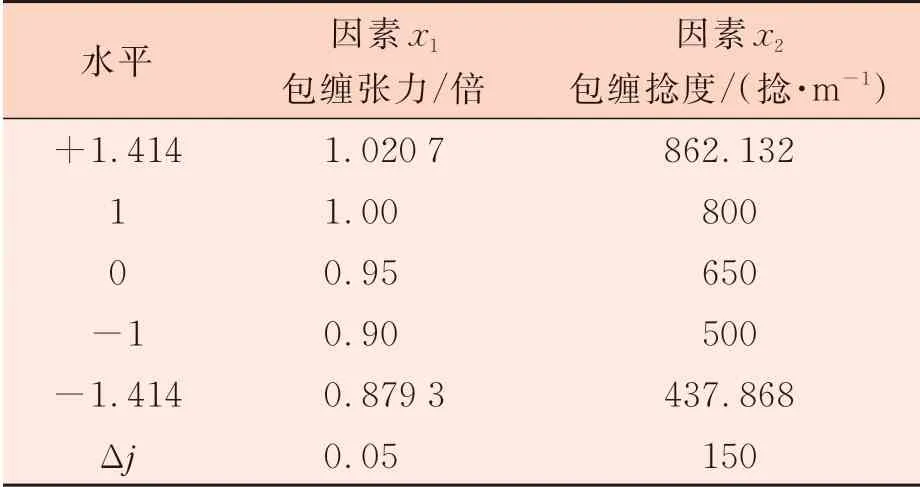
表1 因子水平编码表

表2 试验方案及结果

2 成纱质量指标回归模型的建立

2.1 断裂强力的回归模型

利用Design Expert 软件采用响应曲面法选取包缠捻度和包缠张力两因素进行方案优化设计，其响应值分别为断裂强力及条干CV。由于进行多指标试验结果测试，所以从综合各指标最优值的角度出发，利用方差分析以及回归方程对试验实际值分析得出方程预测值，最后进行工艺参数优化得出最优试验方案。

2.1.1 方差分析及系数显著性检测

二次模型方差分析通过较少的模型得到二次多项式拟合模型方差和回归方程系数分析结果，如表3 所示。若表中所有模型的p值小于0.05，表示该项对断裂强力显著性高；p值小于0.01，表示显著性极高；p值大于0.05，表示显著性不好，需要去掉该项。失拟项越小，其对应的p值越大，表示方程的拟合度越好，p值大于0.05 表明响应值与模型回归方程的关系是好的。

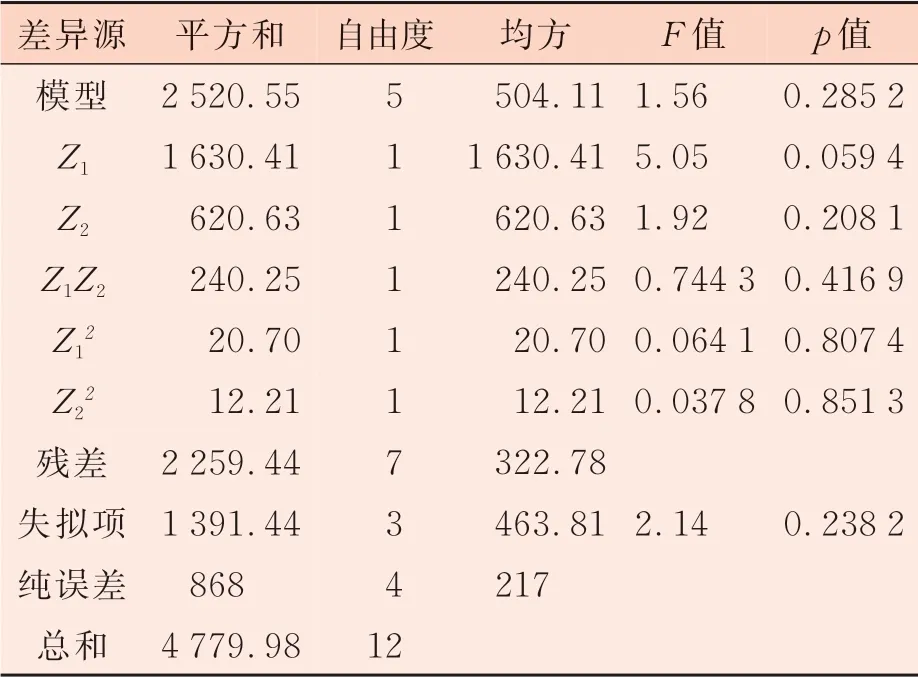
表3 二次多项式拟合模型方差和回归方程系数分析

由表3 可知，模型的p值大于0.05，认为拟合的方程无统计学意义，需对模型进行简化，选择将最不显著项Z2、Z1Z2、Z12、Z22去除，简化模型结果如表4 所示［15］。由二次多项式拟合模型分析结果（p值=0.036 1＜0.05，失拟项p值=0.364 4＞0.05）表明，该模型具有较高的显著性。同时系数Z1在α=0.05 水平上高度显著，因此，可以认为包缠张力对断裂强力影响较大。

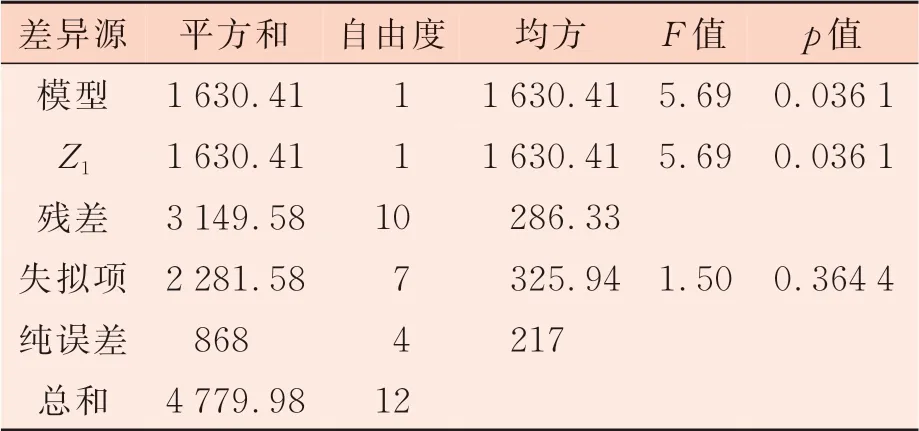
表4 简化模型的方差及回归方程系数分析结果

2.1.2 回归方程的建立

响应面分析过程中数据处理是以已编码数据为基础，即输入的未编码试验因素水平值，软件会将其转化为编码值后，再进行各项统计分析与方程拟合。编码因子表示的系数表如表5 所示。当各因子正交时，VIF为1；VIF大于1，表示多共线性，VIF越高，各因素的相关性越强。

由表5 可得，编码后的方程为断裂强力=280.22+14.28×Z1。 根据编码公式Z1= (x1-x10)/Δ1= (x1-0.95)/0.05，将线性方程y=280.22+14.28×Z1回代得y=280.22+14.28×(x1-0.95)/0.05，则断裂强力的实际拟合方程y=8.9+285.6×x1，可以使用该方程直接进行求解，获得试验最优值与相应的试验条件。

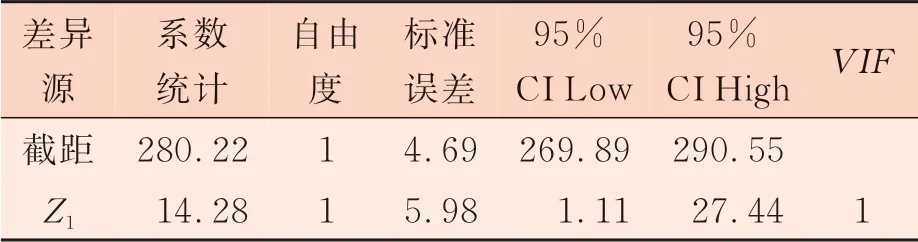
表5 以编码因子表示的系数表

2.1.3 模型的验证

为了验证模型预测的有效性，根据二次多项式拟合方程分析结果可以得到模型对于响应值的拟合度，残差的正态概率分布图越靠近直线越好；残差与方程预测值的对应关系图中分布越分散越无规律越好；预测值与试验实际值的对应关系图越靠近同一条直线越好［16］。对于断裂强力，其残差的正态概率分布靠近直线，如图1 所示。残差与方程预测值的对应分布无规律，如图2 所示。预测值与试验实际值对应靠近同一条直线，如图3 所示。因此试验值与回归方程得到的预测值满足上述规律，拟合度较好，从而可以预测出最佳试验方案。

图1 断裂强力残差的正态概率分布图

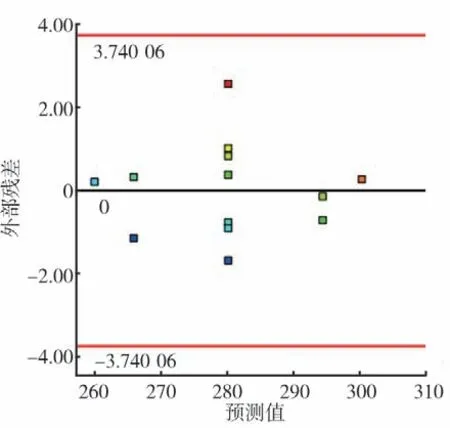
图2 断裂强力残差与方程预测值的对应关系

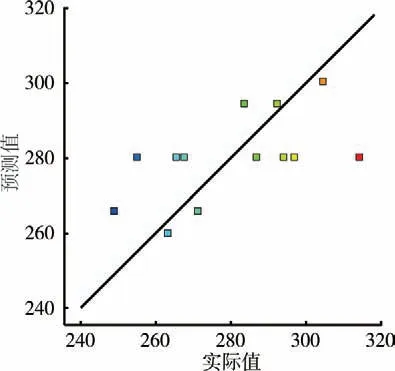
图3 断裂强力预测值与试验实际值的对应关系

2.1.4 响应面分析

响应面图能够非常清楚直观地表现包缠捻度和包缠张力发生变化时对断裂强力的影响，如图4 所示。 可以看出包缠张力对断裂强力作用显著，且呈较强的线性关系。随着包缠张力的增大，断裂强力也随之增大，这说明平行纱的强力主要靠起固纱作用的长丝对芯纤维须条的包缠来获得，当长丝包缠张力较小时，长丝对纱中须条的正压力较小，短纤须条比较松散；当包缠张力逐渐增加时，正压力增加，短纤须条滑脱现象减少，从而使断裂强力增加。而包缠捻度对断裂强度几乎没有影响。

图4 包缠捻度和包缠张力交互影响断裂强力的响应曲面

2.2 条干CV 值的回归模型的建立

2.2.1 方差分析及系数显著性检测

对于响应值条干CV同样经过二次模型的方差分析，如表6 所示。

由表6 可知，回归方程模型的p值=0.032 2＜0.05，认为该模型可用于预测。由于系数Z1、Z1Z2、Z12的p值＞0.05，表明需要对该响应面方程进行进一步优化，去掉不显著项Z1、Z1Z2、Z12，简化后模型如表7 所示。由二次多项式拟合模型分析结果（p值=0.005 2＜0.05，失拟项p值=0.054 5＞0.05）表明，简化后的模型具有很高的显著性。系数显著性结果表明在α=0.05 水平上Z2线性效果十分显著，Z22对条干非线性效果十分显著，因此认为包缠捻度对条干影响较大。

表6 二次多项式模型的方差及回归方程系数分析

表7 简化模型方差分析结果及回归方程系数

2.2.2 回归方程的建立

编码因子表示的系数表如表8 所示。

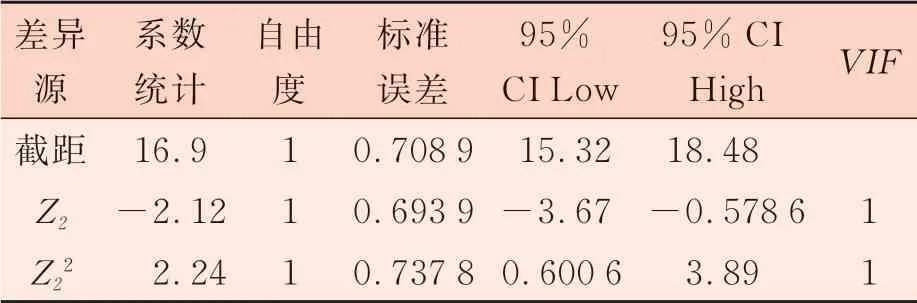
表8 以编码因子表示的系数表

由表8 可得，编码后的方程为条干CV=16.90-2.12×Z2+2.24×Z22。根据编码公式Z2=(x2-x20)/Δ2= (x2-650)/150，将方程y=16.90-2.12×Z2+2.24×Z22回代得到y=16.90-2.12×[(x2-650)/150] +2.24× [(x2-650)/150]2。 则 成纱条干的实际拟合方程就是y=68.148 5-0.143 5×x2+0.000 1×x22。

2.2.3 模型的验证

根据二次多项式拟合方程分析结果来验证模型预测的有效性，可以得到响应值条干CV值残差的正态概率分布较好，如图5 所示。残差与方程预测值的对应无规律，如图6 所示。预测值与试验实际值的对应靠近同一条直线，如图7 所示，因此可以预测出最佳试验方案。

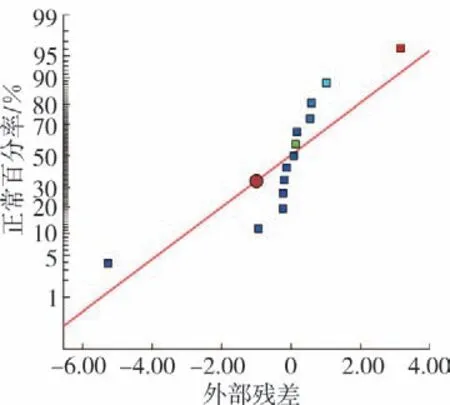
图5 条干CV 残差的正态概率分布图

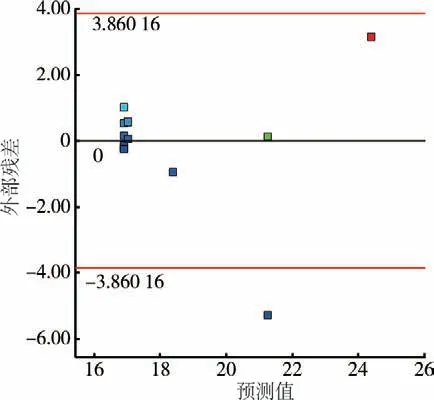
图6 条干CV 残差与方程预测值的对应关系

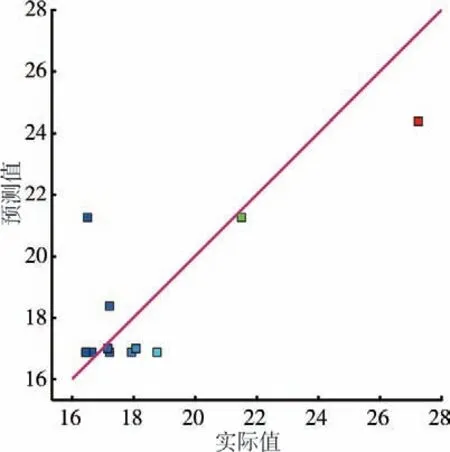
图7 条干CV 预测值与试验实际值的对应关系

2.2.4 响应面分析

包缠捻度和包缠张力交互影响条干响应曲面图如图8 所示。包缠捻度对条干CV作用显著，且呈较强的非线性关系。当包缠捻度较小时，条干CV随着包缠捻度的增大显著降低，这主要是因为包缠捻度增加，长丝螺旋线螺旋角增大，对无捻芯纤维的束缚、覆盖作用增大，使芯纤维结构更紧密，从而使条干改善；当包缠捻度增大到一定程度后，纱线光泽变差，手感变硬，条干CV改善效果趋于平缓；而包缠张力增加，条干CV处于平稳状态。

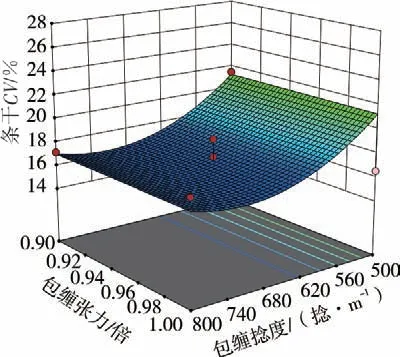
图8 包缠捻度和包缠张力交互影响条干的响应曲面

2.3 成纱质量指标的最优化求解

为减少生产中纱线断头情况，达到与环锭纺相同的断裂功，应根据实际情况合理调整。可以设置试验条件的最低值及最高值，软件预测出最优值，并且提供最优值条件之外的一种或几种方案。 设置好的参数要求如表9 所示。 在设定好优化的约束和目标之后，Design Expert 软件会以列表的形式自动给出优化求解结果，如表10所示。

表9 平行纱工艺参数优化限制条件

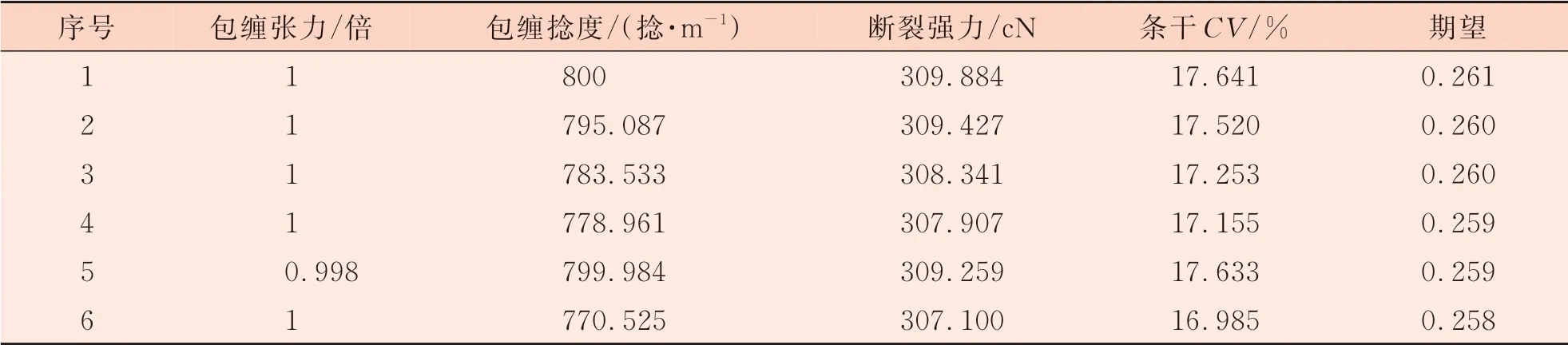
表10 平行纱工艺参数优化方案表

从表10 中得出方案1 为最优，即当包缠张力为1 倍，包缠捻度为800 捻/m，此时平行纺纱线最优断裂强力为309.884 cN、条干CV为17.641%。

3 结论

（1）通过研究平行纺包缠张力和包缠捻度对于平行纱的断裂强力及条干CV值的影响，并利用响应曲面法对其进行二次分析及回归预测，求得断裂强力=8.9+285.6×x1，条干CV=68.148 5-0.143 5×x2+0.000 1×x22，并在此基础上对成纱质量指标多目标求解得到最佳工艺方案：当包缠张力为1 倍，包缠捻度为800 捻/m时，平行纺纱线的断裂强力为309.884 cN、条干CV为17.641%，质量指标较优。

（2）通过分析得到，平行纺纱线的断裂强力与长丝的包缠张力呈线性关系，而与包缠捻度关系不大；纱线的条干CV与包缠捻度呈二次曲线关系，而与长丝包缠张力关系不大。

（3）平行纺纱线由于具有强力高、条干好等特点，在花式纱生产上拥有很大的研究发展潜力。本试验虽然对其纺制中的工艺参数进行了优化，但是受试验条件和环境的限制，平行纺的纱线强力及条干还需要进一步优化来提高。