聚能射流侵彻径向扩孔的可压缩模型*

李 干，陈小伟

（1. 北京理工大学机电学院，北京 100081；2. 北京理工大学爆炸科学与技术国家重点实验室，北京 100081；3. 北京理工大学前沿交叉科学研究院，北京 100081）

在超高速撞击下，材料会因极高的弹/靶界面压力产生不可忽略的体积应变，导致材料密度显著升高，一般需考虑弹靶材料的可压缩性。Song 等已对超高速撞击的弹靶可压缩性的相对强弱有比较分析：一般而言，对较软的金属如铝和铜、非金属靶如树脂类复材和水等，需着重考虑靶材可压缩性的影响；特别地，在高压条件下水和树脂类复材的可压缩性显著强于铝、铜等金属材料的。聚能射流的头部速度可达8～10 km/s 甚至更高，属于超高速撞击。在聚能射流作用下，不同靶体，如金属靶、混凝土或水表现的可压缩性对其侵彻或扩孔的作用不同，相关应用常见于土木防护工程、复合装甲及潜艇/水面舰船。

聚能射流在侵彻中厚靶时会同时进行轴向侵彻和靶材径向扩孔。关于轴向侵彻的理论大致可分为不可压缩模型和可压缩模型，两者的主要区别在于后者考虑了弹/靶材料的可压缩性。不可压缩模型首先由Birkhoff 等提出，Eichelberger考虑了材料强度对Birkhoff 等的理论进行了补充，Allison 等提出射流侵彻的虚拟原点法并结合Birkhoff 等和Eichelberger的理论得到一个不可压缩侵彻模型。可压缩模型主要基于Murnaghan 状态方程和Mie-Grüneisen 状态方程推导而来。Haugstad、Haugstad 等首先基于Murnaghan 状态方程得到可压缩模型，Flis 等基于一种多项级数Mie-Grüneisen 状态方程并结合Allison 等的虚拟原点法得到一个可压缩侵彻模型。Flis采用二次项Mie-Grüneisen 状态方程推导可压缩模型，较Flis 等的状态方程克服了其与冲击波不连续条件并不完全一致的缺陷。考虑到Flis的模型计算比较复杂，Song 等基于Murnaghan 状态方程推导出一个近似解。

关于径向扩孔，Szendrei首先提出一个径向扩孔过程的解析方程，其实用性不强；但他认为射流侵彻的轴向压力必影响射流扩孔的初始径向压力，射流扩孔滞止压力与靶板扩孔速度的关系类比于射流侵彻驻点压力与射流侵彻速度的关系，这2 个论断均为后人所接受。Held 等利用镜框和剖面条纹技术同时记录了聚能装药侵彻射流在水中扩孔的过程并利用实验数据拟合了一个扩孔方程。Held和Held 等在此基础上部分修正了Szendrei 的方程，形成Szendrei-Held 扩孔方程，使其具备实用性；并用该方程的预测结果与实验进行比较，发现模型的预测值偏小，尤其是在高速侵彻部分误差较大。肖强强等在Szendrei-Held 扩孔方程的基础上，考虑侵彻过程中冲击波的影响，进一步改进了前人的扩孔方程。

以上径向扩孔模型均是基于不可压缩模型推导出的。不可压缩模型未考虑靶材的可压缩性则可能造成其在研究高可压缩性靶材侵彻问题时表现不佳。它的缺陷也会影响到扩孔模型的预测能力，Held的研究便发现Szendrei-Held 扩孔方程的预测值小于实验值。同时，径向扩孔模型也是含液密闭结构干扰聚能射流侵彻的理论基础，Guo 等和Zu 等就是以肖强强等的扩孔方程为基础提出了含液密闭结构干扰聚能射流侵彻的理论模型。本文研究的成果也将有助于改进该理论模型，可更好地预测含液密闭结构干扰聚能射流的过程。

本文中，以Szendrei的2 个论断及Flis的可压缩模型为基础，推导出一个径向扩孔的可压缩模型。同时，考虑到完整可压缩模型繁琐的计算过程，又基于Song 等的近似模型推导出一个径向扩孔可压缩模型的近似解，以简化计算流程。将本文模型的预测结果与Held 等的聚能射流水中扩孔实验数据进行比较以验证其可信度，随后再将本文模型代入射流侵彻其他靶材扩孔的研究中，以扩展本文模型的应用范围。

1 可压缩扩孔模型

Szendrei-Held 扩孔方程虽然填补了该领域的理论空白，但因其建立在不可压缩模型的基础上，承袭了靶材密度不变的假设，导致该理论在预测可压缩性较强的靶材（如水）的扩孔时表现不佳。尤其是Held的实验数据总是高于Szendrei-Held 扩孔方程的预测值，这即为本文中要解决的关键问题。

不可压缩模型不仅忽略材料在侵彻与扩孔过程中的形变，还未考虑材料的内能、压力变化。Flis的可压缩模型除考虑了上述情形，还增加了材料从冲击波界面至弹/靶分界面过程的分析。这2 个分界面的位置如图1 所示，记冲击波分界面前下标为状态0 也即初始状态，分界面后下标为状态1，弹靶分界面处下标为状态2，j 代表射流，t 代表靶材，为聚能射流速度，为侵彻速度。不可压模型是直接从状态0到状态2，而Flis的可压缩模型则在此基础上考虑了状态0 到状态1 的过程，并假设从状态1到状态2 的内能变化是等熵变化。

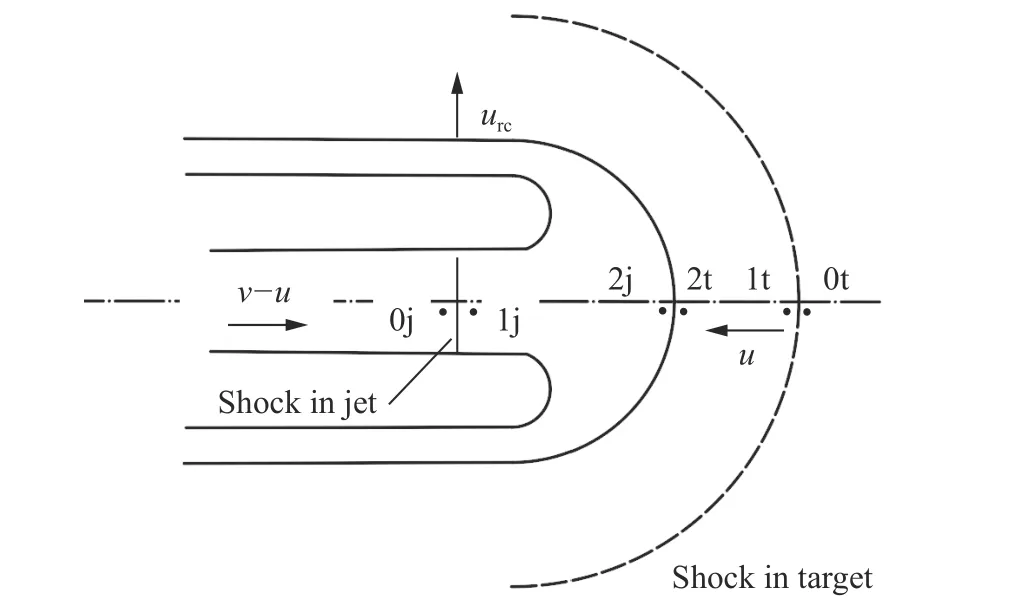
图1 侵彻速度与扩孔速度分布及侵彻过程中的流场Fig. 1 Distribution of penetration velocity and radial crater velocity, flow field during penetration

本文模型推导承袭Szendrei的2 个论断：射流侵彻的轴向压力必影响射流扩孔的初始径向压力；射流扩孔滞止压力与靶板扩孔速度的关系类比于射流侵彻驻点压力与射流侵彻速度的关系。在此基础上，考虑Flis的可压缩模型的可压缩特性，推导出一种新的扩孔方程。

对于扩孔滞止压力与相应速度的驻点压力的关系，Szendrei认为其压力与面积的乘积为一常数。本文中仍然沿用这一假设，则滞止压力与该速度下的驻点压力的关系为：

结合式(4)和式(6)可知，射流半径、驻点压力、靶材强度、驻点处靶材密度是影响聚能射流扩孔的主要因素。

式中：为重力加速度，为水的深度。则可将液体类靶材其最大扩孔的影响因素进一步总结为射流半径、驻点压力和液体深度。

基于射流侵彻的可压缩模型及Szendrei的2 个论断，得到一个考虑材料可压缩性的聚能射流扩孔模型。Szendrei-Held 模型中的式(4)采用不可压缩模型的驻点压力并认为靶材密度始终不变，而本文模型的驻点压力采用了可压缩模型的驻点压力，密度采用了弹/靶分界面处靶材密度。本节模型的关键在于求解驻点压力和弹/靶分界面处靶材密度ρ，两者的求解方法需参考Flis的文献。相较于前人的模型，本文模型考虑了弹/靶材料的可压缩性，可以更准确地预测靶材尤其是高可压缩性靶材的扩孔情况。

Flis的可压缩模型需考虑2 个变化过程，而且第2 个过程的求解比较繁琐，需要循环积分和判断，不太适合于工程计算，尤其是上述2 个系数的求解更复杂，这极大地限制了该模型的实用性。因此，需寻找一种更简便的方法求解这2 个参数。

2 可压缩模型的近似解

Song 等曾基于Murnaghan 状态方程推导出可压缩模型的一个近似解，该近似解结构简单，只需要采用牛顿迭代法即可求得侵彻速度，进而可以较容易地求解驻点压力和弹/靶分界面处靶材密度ρ。Li 等证明采用该近似模型对射流侵彻水也可以进行有效预测，因此本文中采用该模型求解上述2 个参数。

将侵彻速度代入式(14)和式(20)即可分别求得和ρ，由此将这2 个参数代入式(4)即为扩孔模型近似解，该近似解使求解扩孔速度及其他参数更简便。

3 实验验证与分析

经过上文的推导，可以得到一个基于材料可压缩性的聚能射流扩孔模型和其近似解，则在本节将本文模型与Held 等的计算和实验数据进行比较。

选取Held 等的实验中射流速度=6 700 m/s、射流半径=0.5 mm、水深=100 m 的情况与本文理论进行对比，从而验证本文理论的合理性。Held 等的实验数据中扩孔初始半径均以射流半径为起始量，则本文中也认为射流半径即为扩孔初始半径。由于本文的模型计算均需材料的Mie-Grüneisen状态方程，表1 给出了铜和水的参数以及后续其他材料的参数：初始密度ρ、初始声速、常数和、Grüneisen 系数Γ。为了验证本文模型的可信度，将本文模型的预测结果与Held 等实验中0～60 μs 的实验观察结果进行比较，结果如图2 所示。

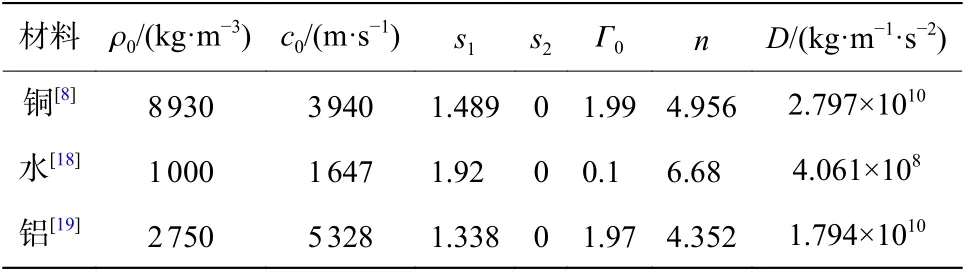
表1 材料的Mie-Grüneisen 状态方程和Murnaghan 状态方程参数Table 1 Material parameters of Mie-Grüneisen and Murnaghan equations of state

图2 表明，在初始阶段（0～10 μs）本文模型的预测结果基本与实验结果相同。随着时间的增加，Szendrei-Held 模型的预测结果与实验结果的误差逐渐增大，其预测值逐渐小于实验值。而随着时间的增加，本文模型的预测值略高于实验值，但其误差显著小于Szendrei-Held 模型，可见本文模型对于液体扩孔过程的预测能力较强。

图2 不同方法获得的扩孔孔径随时间变化的比较Fig. 2 Comparison of crater radius varying with time among different methods

然而Held 等未观察到水的最大扩孔半径，仅通过Szendrei-Held 模型计算出最大扩孔半径及达到最大扩孔半径所用的时间。表2 即为Held 等的计算结果与本文模型计算结果的比较，计算了上述条件下的扩孔最大半径和扩孔达到最大半径所用的时间。由表2 可得，采用可压缩模型和近似解求得的和值分别约为采用Szendrei-Held 模型求得的相应数值的2/3 和1/2。因此，根据式(7) 求得的最大半径较Szendrei-Held 模型求得的最大半径增大了9.8%，且考虑材料的可压缩性使达到最大扩孔半径所用的时间增加约45.7%。

表2 不同模型的相关参数和计算结果的比较Table 2 Comparison of relevant parameters and calculation results among different models

另外，根据式(7)得到靶材最大扩孔半径与水深度的关系曲线（见图3）和靶材最大扩孔半径与射流半径的关系曲线（见图4）。这2 个图均显示本文的模型计算结果的变化趋势与Held 等计算结果的变化趋势相同。在图3 中，根据式(7)可知最大扩孔半径与水的深度之间呈指数关系，且靶材强度越低（越接近水面）其扩孔半径越大；当靶材强度为零（聚能射流在水面侵彻时），扩孔半径趋于无穷大。在图4 中，当水深一定（即靶材强度相同）时，聚能射流的半径与靶材的扩孔半径呈线性关系。相关分析与Held 等的计算结果相吻合。另外，由式(15)可知驻点压力的主要影响因素为聚能射流速度，而这也是影响最大扩孔半径的重要因素。

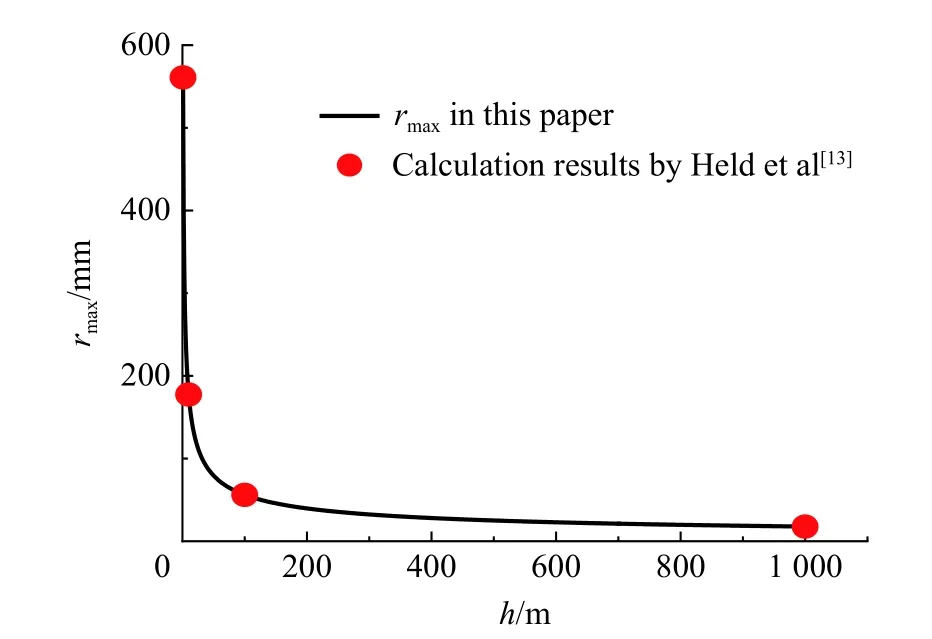
图3 靶材最大扩孔半径与水深度的关系Fig. 3 Relationship between the maximum target crater radius and the water depth

图4 靶材最大扩孔半径与射流半径的关系（h=10 m）Fig. 4 Relationship between the maximum target crater radius and the jet radius (h=10 m)

4 讨 论

Held 等曾经将Szendrei-Held 模型运用于射流侵彻铝靶和玻璃钢靶扩孔问题的研究，发现该模型的预测值与实验数据的吻合度较高。为验证本文模型与Held 等实验数据的吻合度，将铜射流侵彻铝靶实验的最大扩孔半径与本文模型的预测值进行比较。铝的状态方程参数见表1，Held 等的实验所用射流的半径为0.71 mm，铝靶的强度为300 MPa，比较结果见表3。

表3 不同方法获得的铜射流侵彻铝靶最大扩孔半径的比较Table 3 Comparison of the maximum target crater radii for copper jets penetrating aluminum targets by different methods

由表3 可以看出：在较低速度（=6 100 m/s）下，本文模型的预测结果与Szendrei-Held 模型的预测结果几无差别；较高速度（=7 600 m/s）下，本文模型的预测值比Szendrei-Held 模型的预测值略大，Szendrei-Held 模型的预测值更接近实验结果；而中间速度（=6 750 m/s）下，本文模型的预测值更接近实验结果，Szendrei-Held 模型预测与实验结果有一定误差。同时本文中也注意到实验数据中7 600 和6 750 m/s 速度下的扩孔半径差异太小，按插值分析，有理由怀疑其合理性，但无法证实，期待未来有更多的实验数据来验证本文模型。本文中认为，Szendrei-Held 模型可能不太适合预测高可压缩性靶材的径向扩孔，但仍适用于低速侵彻可压缩性较弱的靶材扩孔情况。

另外，由式(4)可知，除射流半径和靶材强度这2 个因素外，驻点压力的改变也会使模型预测结果发生变化。为便于分析不同驻点压力对模型预测精度的影响，将表1 中的材料参数代入Hugoniot 压力函数：

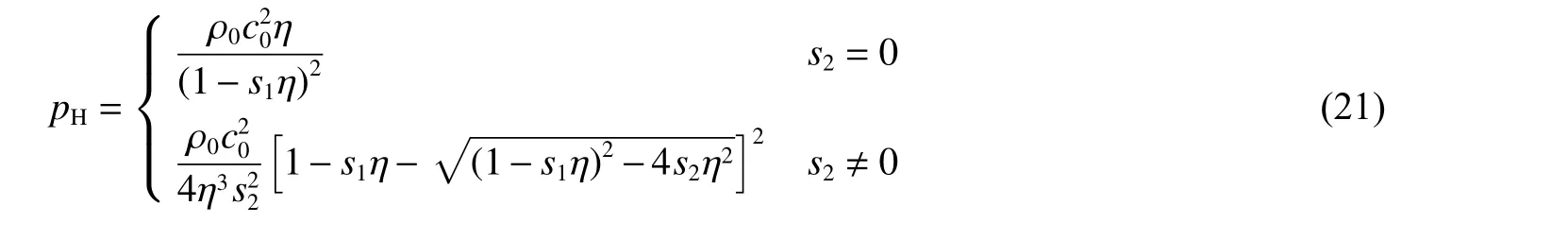
水、铜和铝3 种材料的Hugoniot 压力曲线如图5 所示。由图5 可知，水的可压缩性远强于铜和铝的，而后两者的可压缩性较接近。而图6 展示了射流侵彻水和铝靶过程的驻点压力变化，从图中可以看出，射流侵彻水的界面压力比射流侵彻铝靶的界面压力低。即便如此，由图5 可知，相同的射流侵彻条件下，水的可压缩性也显著强于铝靶的。

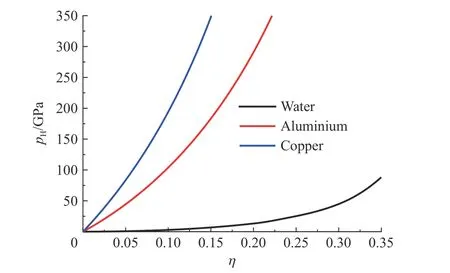
图5 水、铝和铜的Hugoniot 压力曲线Fig. 5 Hugoniot pressure curves for water, aluminium and copper

图6 射流侵彻靶材的驻点压力随射流速度的变化Fig. 6 Stagnation point pressure of jets penetrating targets varying with jet velocity

另外，由图6 可知，可压缩模型的驻点压力高于不可压缩模型的驻点压力，两者的差值随着射流速度升高而增大。也即：在较低射流速度时，本文模型可退化为不可压模型的分析。

5 结 论

首先，基于Flis的可压缩模型推导出考虑弹/靶材料可压缩性的聚能射流扩孔模型；然后，参考Song 等的工作得到一个模型近似解。该模型与Szendrei-Held 模型结构相似，且与Held 等实验结果较吻合，可见聚能射流扩孔的研究需考虑弹/靶材料的可压缩性。近似解使得驻点压力和驻点处靶材密度的求解更简便。

基于本文的模型分析可得影响聚能射流扩孔的因素有射流半径、驻点压力、靶材强度、驻点处靶材密度以及聚能射流速度。相应的，Szendrei-Held 模型的主要缺陷是未考虑靶材的密度变化。

相较而言，射流侵彻可压缩性较差的靶材（如金属类），Szendrei-Held 模型的预测性与本文模型相当，但针对可压缩性较强的靶材（如液体类、树脂类），Szendrei-Held 模型的预测性不如本文模型。另外，在高速侵彻中，本文模型预测性优于Szendrei-Held 模型。结合理论分析，在聚能射流低速侵彻可压缩性较差的靶材时，仍然可以采用结构较简单的Szendrei-Held 模型；而在高速侵彻可压缩性较强的靶材时，建议采用本文模型。