Wavelet-VMD 融合算法在管道泄漏检测的研究与应用

郭 颖，杨理践，唐滕达

（1.沈阳工业大学信息科学与工程学院，辽宁沈阳 110870；2.辽宁石油化工大学信息与控制工程学院，辽宁 抚顺 113001）

随着工业4.0 时代的到来，我国能源需求量大幅增加，现如今国内油气管网总里程已达16.9万公里[1]。但是，管道在运行的过程中，由于常年使用，不可避免地会发生许多不可控的因素，如：腐蚀、老化以及人为破坏等，都将会导致管道发生泄漏。当管道发生断裂和泄漏时，将会发生环境污染和爆炸等危险，给国家带来巨大的财产损失及资源浪费[2-4]。泄漏检测方法评价指标通常包括灵敏度、定位精度、误报率/漏报率等，经横向比较，最终选用次声波法作为管道泄漏检测的检测方法。

由于次声波信号中含有大量的干扰噪声，需要对其进行降噪处理。但因信号特征等其他因素的影响，小波变换对于非平稳信号的降噪效果不太理想，使用范围比较有限。EMD 可以将次声波信号从高频到低频逐一分解成IMF 分量与余项的和，在不使用选取基函数的前提下，利用模态的选取来进行降噪处理。但是，从实际的降噪效果上看并不如小波阈值法，EMD 更加适用于对高频信号的降噪处理。而VMD 与EMD 相反，是从低频到高频逐一进行分解出各模态分量，然后选择合适有效的IMF 分量进行重构初始信号[5]。在采用声波法进行管道泄漏检测时，VMD 的抑制模混叠的情况优于EMD,并且其降噪效果更加理想。

1 次声波管道泄漏检测方法

上个世纪七十年代在巴黎举办的国际噪声专业会议上次声波概念首次被提出，并将频率在20 Hz 以下的声波称为次声波。虽然在此之前就已经发现了次声波的存在，但是并没有得到广泛的重视。次声波的波长较长，在空气传播中不易被介质所吸收且穿透能力强。频率越低时，次声波的传播距离越远，由此可以得出次声波的波长与频率间的关系成反比，非常适用于在长输油管道中检测并接收[6-7]。

石油或天然气在运输过程处于管道内部的压力环境中，管道在平稳运行过程中，管道内部的流体压力要远远小于管道壁所承受的膨胀力，如果内部压力大于管壁的承受力时，将会产生泄漏。当输油管壁的某一处突然发生破裂时，管壁会向外发生扩张，管道内部的介质由于内部和外部压力差的作用下，管道内部的油品瞬间自破裂处的洞孔向外喷出与管壁发生摩擦，从而使空气产生振动发出次声波。该声波信号会沿着管道的上下游进行传播，最终传递到管道两端的次声波传感器，然后将收集到的数据上传给中央处理器，并对信号进行处理和分析，从而判断该处是否发生泄漏，然后计算该信号到达两个传感器所用的时间差，从而精准地计算出管道泄漏处所在的具体位置[8-10]。如图1 所示。

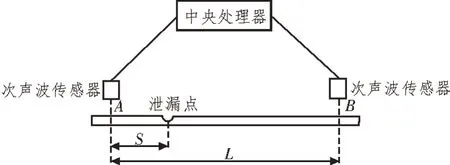
图1 次声波采集设备示意图

次声波定位计算公式如下所示：

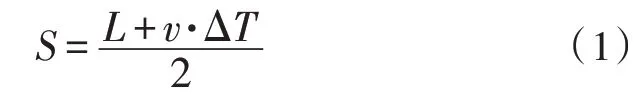
式中，L表示为A传感器安装位置与B传感器安装位置之间的距离，单位为m；S表示为管道泄漏点处所在的位置距离A传感器安装位置间的距离，单位为m；T1和T2分别表示次声波到达传感器A和传感器B所在位置所用的时间，单位为s；ΔT表示传感器A和传感器B接收到泄漏信号的时间差值，单位为s；v表示管道泄漏时所产生的次声波波速，单位为m/s。

2 次声波的信号处理

管道泄漏时除了会产生次声波信号源外，还会产生许许多多不可控的干扰噪声因素，应该采取相应的方法来抑制噪声干扰。怎样才能去除掉次声波信号中所夹杂的干扰噪声信号，从含有干扰噪声的次声波信号中分离出有效泄漏特征信号，成为管道检测研发的重要难点。如果不减少干扰噪声对泄漏所产生信号的影响，不利于对泄漏点进行精准定位，导致其结果会产生较大的误差，不能准确找到管道泄漏时的位置所在。

通常都会选用小波变换对非平稳随机信号进行降噪处理使有用信号显现出来，但是母小波等因素将会影响小波降噪的效果，自身的使用范围受到很大的限制[11]。EMD 算法可对初始信号进行线性化和平稳化处理，在小波变换的基础上，避免了降噪时选用基函数的弊端，但是其降噪效果不如小波降噪，而且在进行信号处理时还会产生模态混叠的现象[12]。VMD 算法在降噪分解中改善了EMD 算法在降噪分解过程中出现模态混叠的现象，通过寻找各模态的中心频率对初始信号进行重构[13]。该文将Wavelet与VMD 相融合，对管道泄漏时所产生的次声波信号进行降噪处理，并进行仿真实验，验证其优越性。

2.1 小波降噪方法研究

小波变换已逐渐成为时变系统滤波的最为有效的数学分析工具，由于多分辨、时频域局部化和在不同的分辨水平上可以重新构造信号特性，不仅可以用小波作为基函数来构造函数，还可以是时域与频域的分析工具。在保留傅里叶变换所具有优点的同时，还在其基础上，对时间域和空间域变换到小波域的局部化分析，将能量的有限信号进行分解，使其变为震荡性函数且具有快速衰减的特性，通过伸缩平移得到小波基函数的过程[13-14]。其变换公式为：

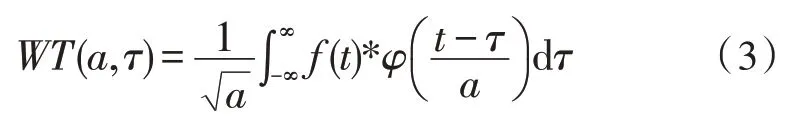
式中，a为小波变换尺度，用来控制小波函数的伸缩量；*表示卷积；τ为平移量，用来控制小波函数的平移。

2.2 EMD降噪方法研究

EMD 即经验模态分解是Huang 希尔伯特变换的重要部分，其分解原理主要是依靠本身所固有的时间尺度特征，没有任何的基函数用来依靠，具有很好的自适应能力。但是，实际上是把不同频率的分量经时间尺度由小到大一步步从原始信号中分离出来的过程，将所得到的不同频率分量将其称之为固有模态分量（IMF），这些IMF 分量可将初始信号的局部细节清楚地展现出来[15]。其公式如式（4）所示：

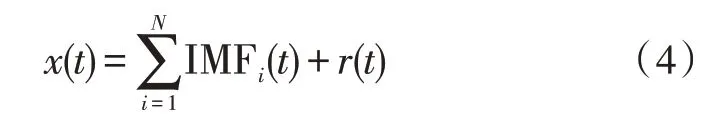
式中，IMFi(t)为分解后所得的第i个IMF 分量；r(t)为残余项，N为IMF分量的数目。N的含义主要是经过初始信号分解后所得出的残余分量，表示信号的趋势。

2.3 VMD降噪方法研究

常用的EMD 泄漏信号降噪方法无法解决各个分解模态之间的混叠问题，且在筛选过程中信号两端不可能同时处于极大值和极小值，所以在信号的两端不可避免地会出现发散现象。2014 年Konstantin Dragomiretskiy and Dominique Zosso 等研究者提出了新的信号处理方法VMD，该方法使用迭代搜索的方式来寻找经过VMD 分解后的各个分解模态的带宽和中心频率，这些分解模态分解出了平滑的基带，也就证实了VMD 更具有鲁棒性[16]。

VMD 算法将信号f(t)分解为一系列具有特定稀疏特性的独立模态函数uk(t)，每个独立模态的载频都紧围其中心频率ωk，且可利用这些独立模态实现信号重构[17]。其公式如下：

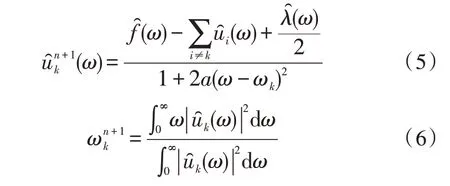
3 实验分析与结果

为了验证所提出方法的可行性，所设计的实验全过程在环形管道实验平台进行研究。与此同时实验为了考虑安全性以及成本方面的因素，在实验中均用水来代替油品，从而进行管道泄漏检测实验。全长为2 800 m 的实验管道上一共有14 个规则的圆形钻孔，每间隔200 m 有一个规则的圆形钻孔作为管道泄漏点，管道的压力设计为1.6 MPa，但在实际运行过程中其压力为1.2 MPa，将采用离心泵对水进行增压，然后流入实验管道内部，在管道中分别配置不同位置球阀，而且球阀的孔径都有所不同，以此来模拟管道泄漏的发生。该文分别就实验平台管道泄漏点孔径Ф4（相当于泄漏孔径为2 mm）和孔径Ф6（相当于泄漏孔径为3 mm）在开泵状态下进行研究。在实验的过程中，由于是手动调节阀门，可能会使泄漏量在大小上存在一些误差。现场的实验环境如图2所示。

图2 环形实验场地示意图

在此基础上，将会对所采集到的数据进行仿真实验，并通过对Wavelet-EMD、VMD-wavelet 以及Wavelet-VMD 三种降噪方法的进行对比，以此来判断所提出的降噪方法的优越性。

下面通过在泄漏点位为1 400 m 的情况下，对开泵运行状态下泄漏点孔径为Ф4 与Ф6 进行研究，采用的降噪方法如下：

1）Wavelet-EMD

首先将实验所采集到的次声波数据利用小波阈值的方法进行降噪，然后对提取出的信号数据作EMD 分解。降噪后的Ф4 与Ф6 结果如图3、图4所示。

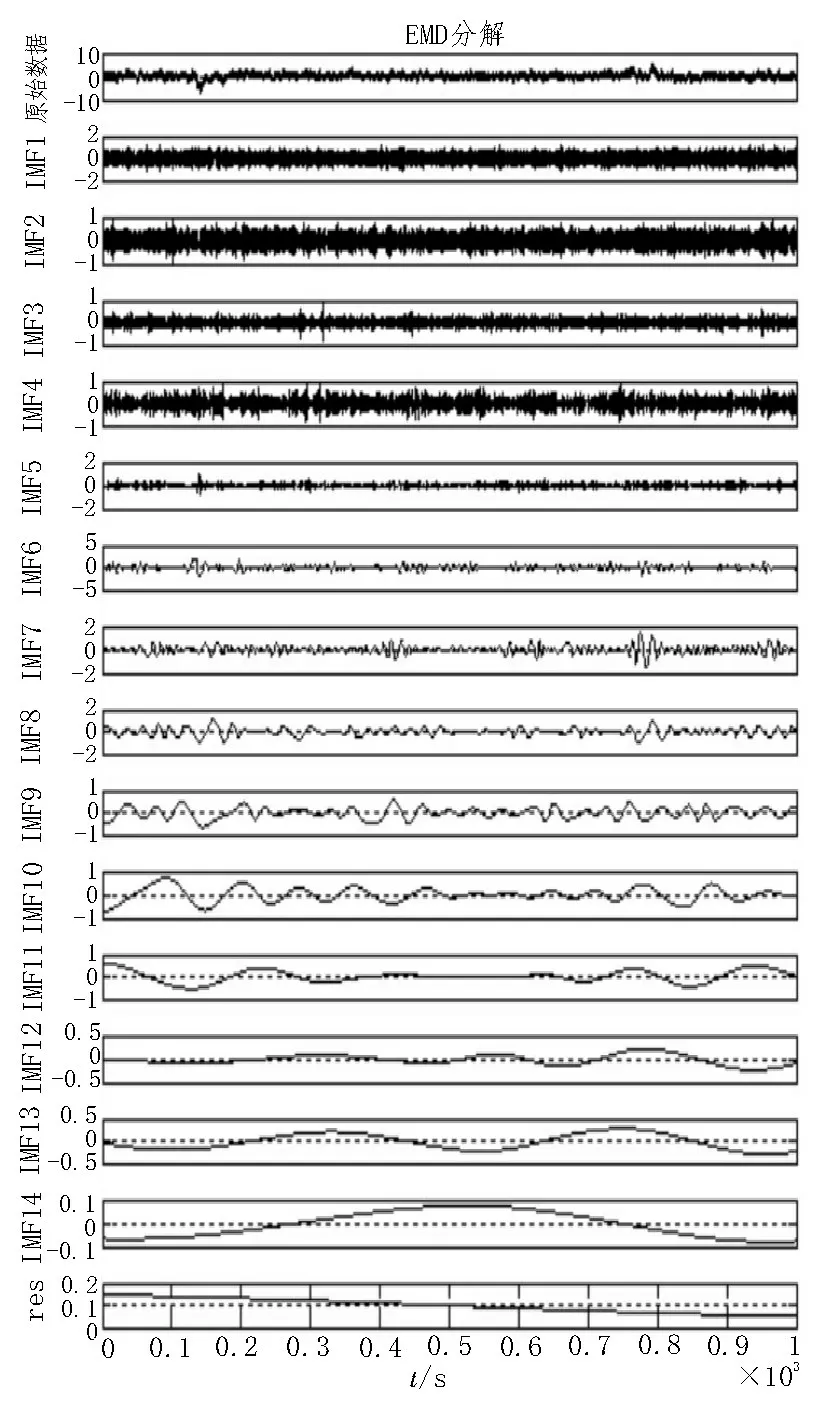
图3 Ф4降噪后的示意图

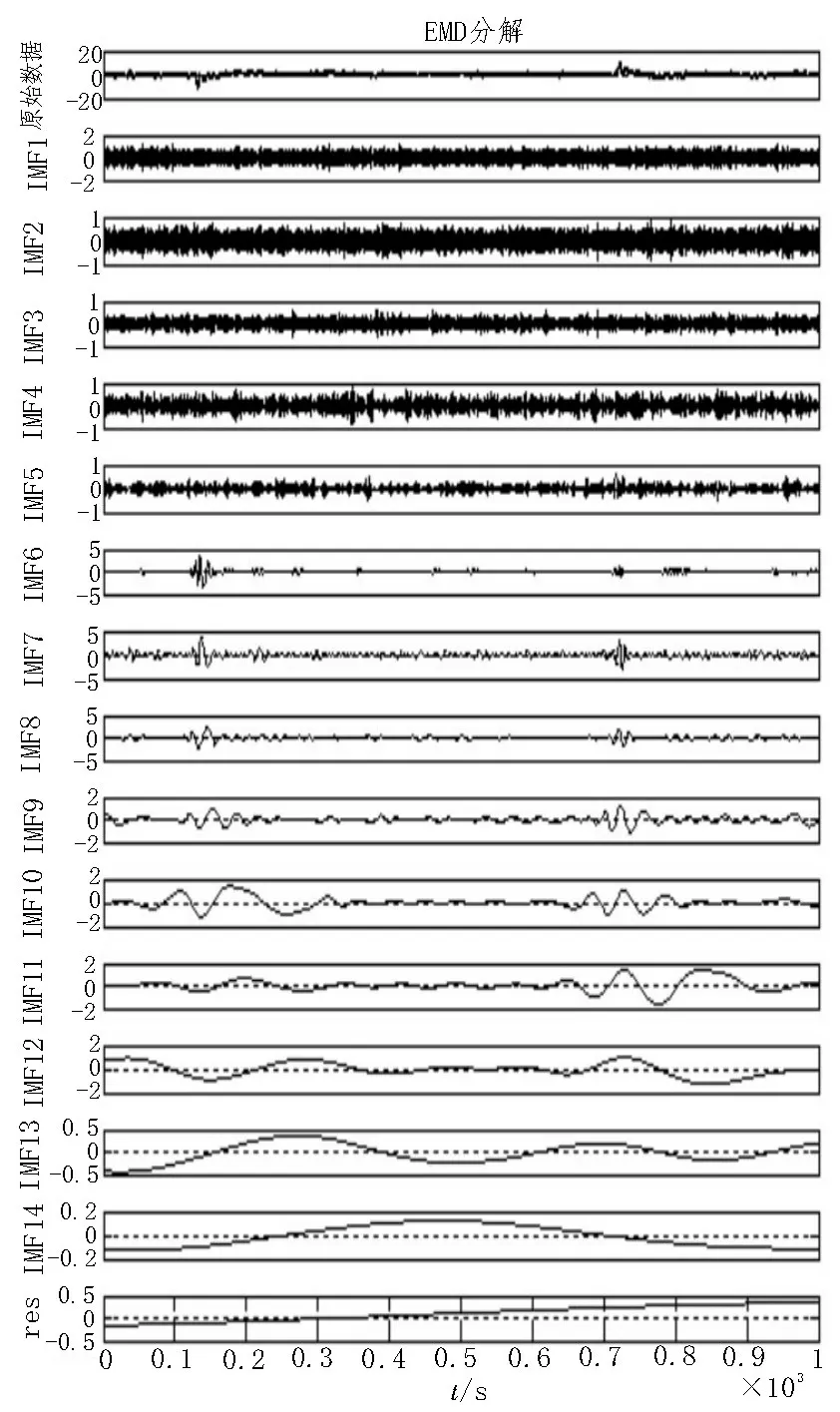
图4 Ф6降噪后的示意图

2）VMD-Wavelet

将所采集的数据先经过VMD 分解，降噪后所得到的新数据，将降噪后的数据代入到小波阈值降噪进行二次降噪。降噪后的Ф4 与Ф6 结果如图5、图6所示。

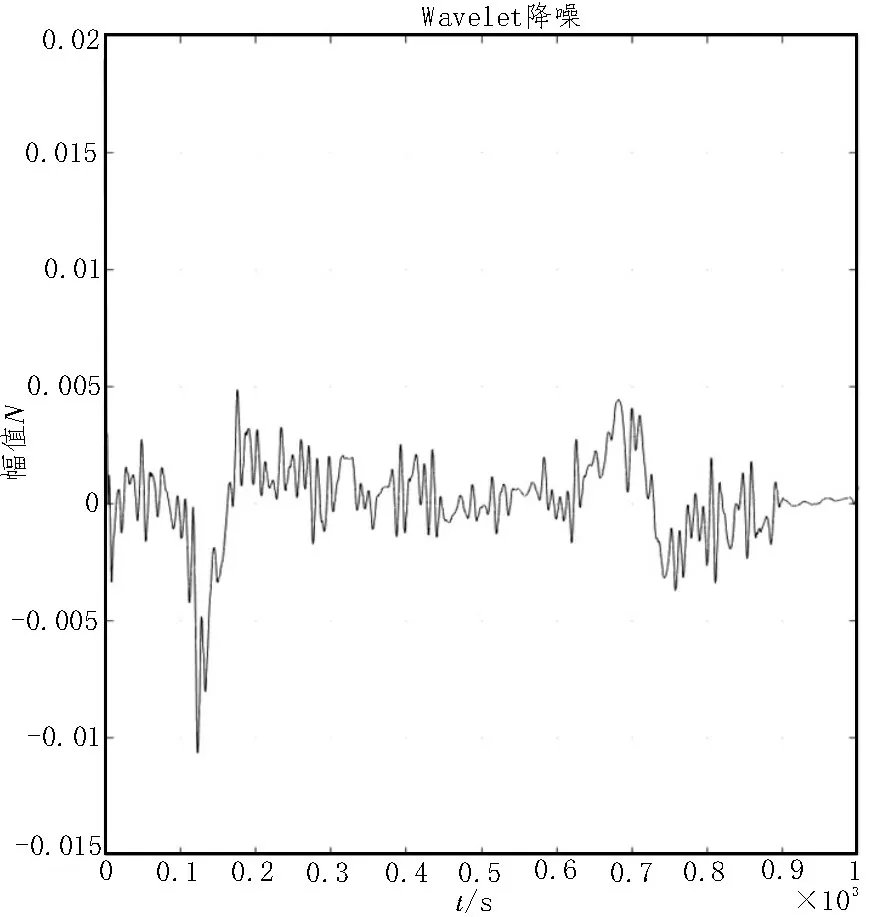
图5 Ф4降噪后示意图

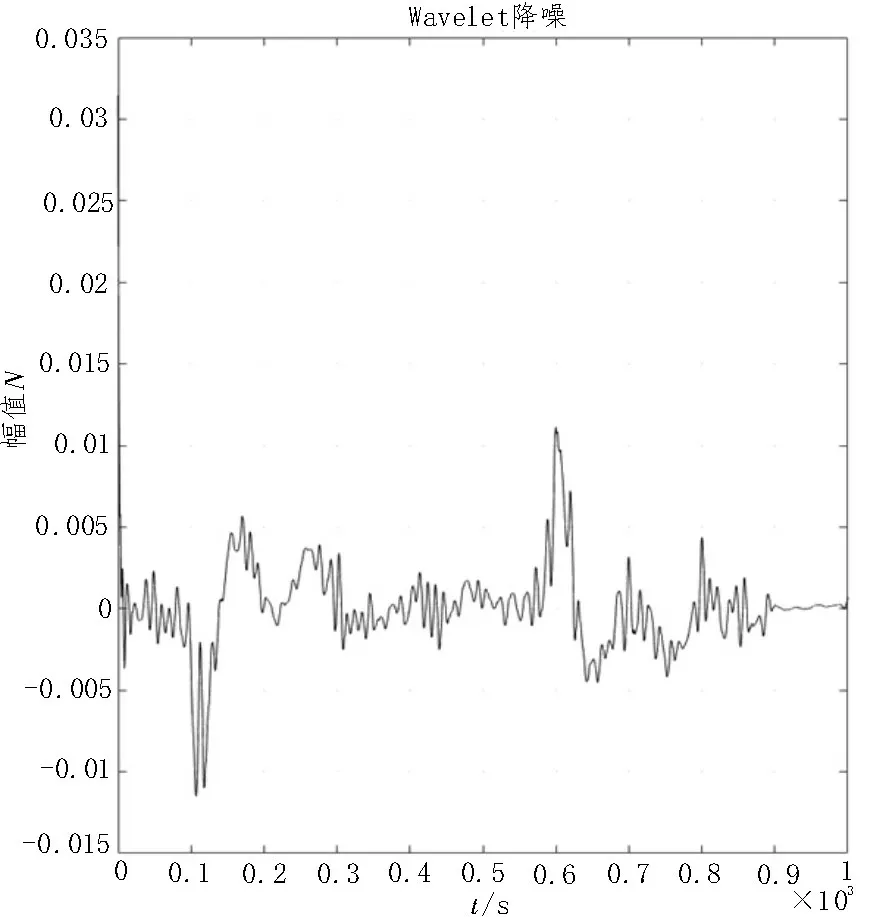
图6 Ф6降噪后示意图

3）Wavelet-VMD

将采集到的实验数据先经小波阈值降噪处理产生一个新的数据，并将新数据代入VMD 进行分解降噪。降噪后的结果如图7、图8 所示。

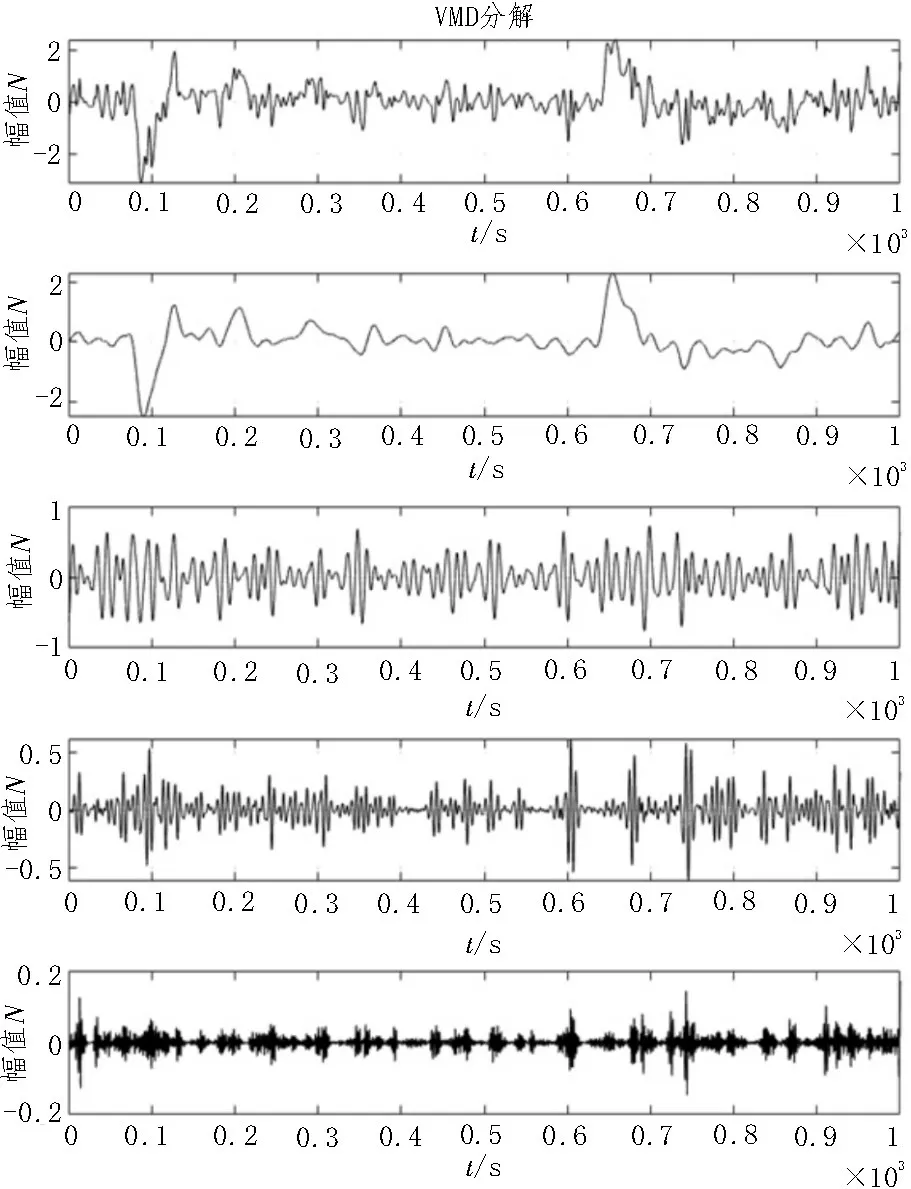
图7 Ф4降噪后示意图

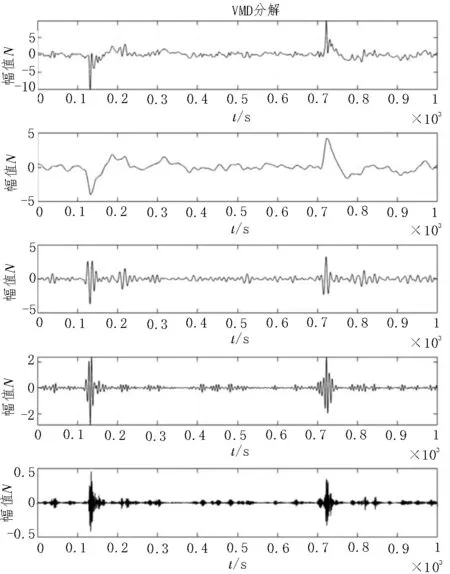
图8 Ф6降噪后示意图

根据管道首末两端次声波传感器所获得突变信号的时间差值，结合首末端次声波传感器之间的距离以及次声波信号在管道中的传播速度，进而确定管道泄漏处的准确位置，实现精准定位。在1 400 m泄漏位置应用三种算法所得到的孔径Ф4、Ф6 位置估计结果如表1 所示。

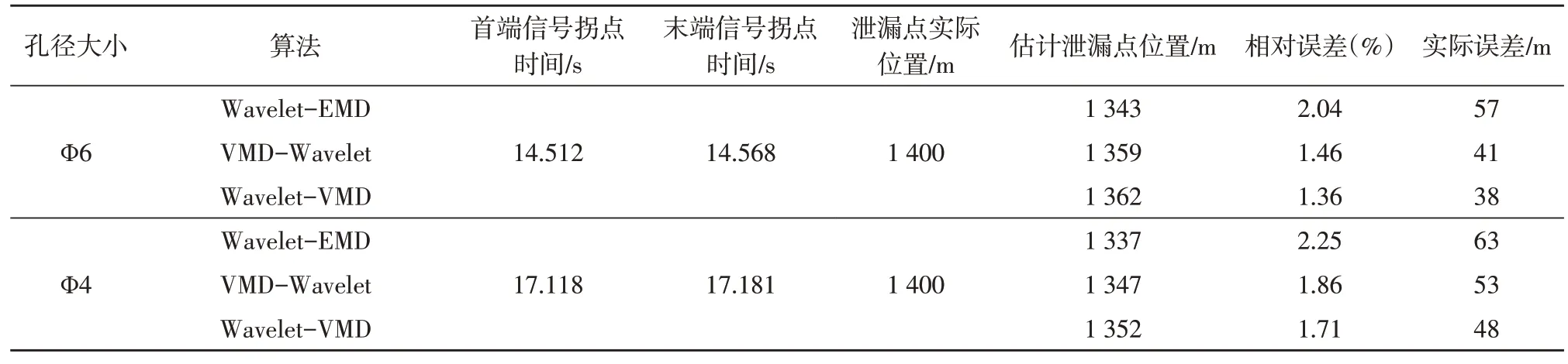
表1 实验管道泄漏点位置估计结果

为了可以更清楚直观地观测表中数据，整理后泄漏点位置的相对误差示意图如图9 所示。

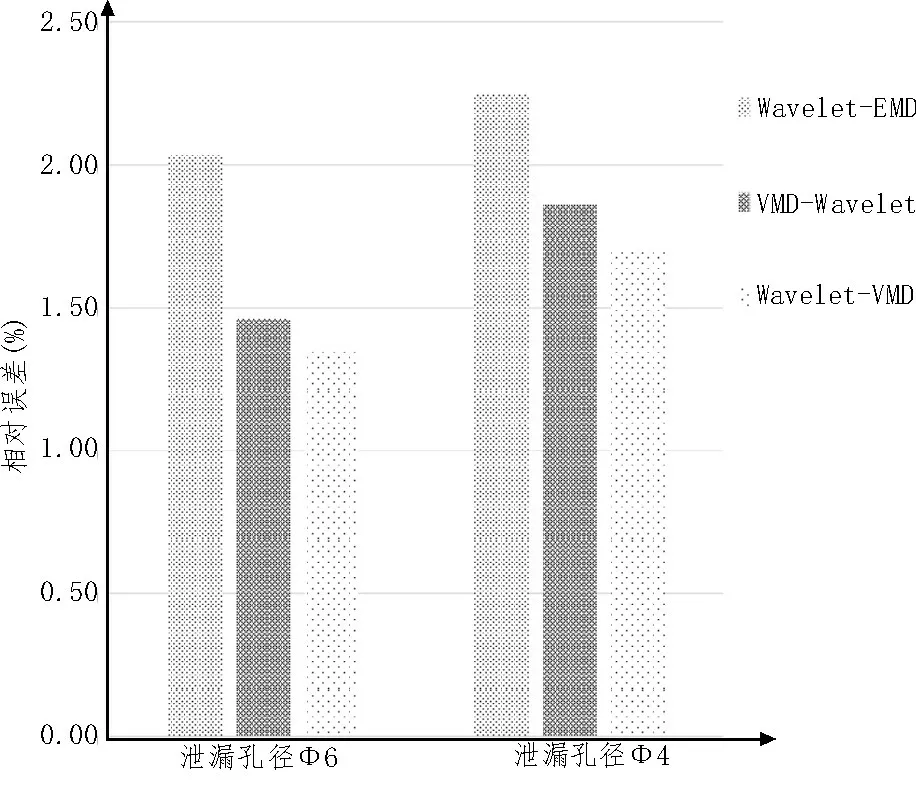
图9 泄漏点位置的相对误差示意图

4 结论

该文采用算法融合的思路，在现有小波阈值降噪的基础上，对比EMD 和VMD 分解算法，提出了Wavelet-VMD 融合降噪的算法。并且通过实验在开泵状态下所采集的次声波数据为依据，对其进行判断对比，验证Wavelet-VMD 的降噪效果，其结果表明在相同的泄漏孔径下，使用Wavelet-VMD 降噪算法优于Wavelet-EMD 降噪算法和VMD-Wavelet 降噪算法。但是，在泄漏孔径增大时，Wavelet-VMD 与VMD-Wavelet 算法差别不大。在使用相同的降噪算法时，孔径会对次声波信号的定位精度产生一定的干扰，泄漏孔径越大定位精度越准确。由此可见Wavelet-VMD 的降噪具有可行性，并有效地提高定位精度。