基于BLF 全状态约束的直接横摆力矩控制

何友国，程勇，袁朝春

（江苏大学汽车工程研究院，江苏镇江 212000）

随着汽车工业的不断发展，汽车主动安全已成为汽车行业的重要研究方向[1]。直接横摆力矩控制作为一种主动安全控制方法，已被证明能显著提高车辆的操纵稳定性[2]。DYC 控制是通过控制两侧车轮制动力之差产生横摆力矩来控制车辆的行驶状态，使车辆在危险工况如高速度方向盘快速转动下保持稳定状态[3]。目前，DYC 控制策略主要有模糊控制、PID 控制和滑模控制等。文献[4-6]提出的模糊控制是一种不依赖于被控对象模型的控制算法，因其鲁棒性强被广泛应用于非线性系统的研究中。但是，模糊控制算法直接对信息进行模糊处理，相对依赖经验，会导致控制精度的减少。文献[7]中PID 控制较为传统，控制效果稳定，对固定模型和平稳变化的工况有较好的控制效果。文献[8-9]中滑模控制克服了模糊控制和PID 控制受控对象系统结构固定的限制，具有响应速度快的优点。上述方法中，在控制过程中均未考虑到质心侧偏角和横摆角速度两个状态量的安全约束边界。

针对状态量质心侧偏角和横摆角速度过大,或超调会产生车辆横向失稳的可能性，大量学者研究了诸多车辆行驶稳定的判定方法。文献[10-12]基于质心侧偏角和质心侧偏角速度相平面法,以稳定区域内菱形的4个端点确定可公式化的车辆质心侧偏角的稳定区间。上述研究为车辆DYC 控制介入控制[12-15]提供了准确的公式化依据。但是，上述方法仅是将质心侧偏角和横摆角速度的约束边界作为阈值，在接近或超过边界时启动DYC 控制，仍会出现质心侧偏角和横摆角速度违反约束边界而引起车辆失稳的可能性。

综上所述，该文针对以往DYC 控制中不能严格约束车辆状态量的质心侧偏角和横摆角速度在其稳定区间的问题，将质心侧偏角和横摆角速度的约束边界直接融入控制器的设计中，基于BLF 函数提出了全状态约束的直接横摆力矩控制策略。

1 系统模型的建立

1.1 汽车二自由度理想模型

假设两侧车轮的运动情况相同，车辆模型可以简化为如图1 所示的车辆二自由度理想模型，模型只有横向平移和横摆运动两个自由度。

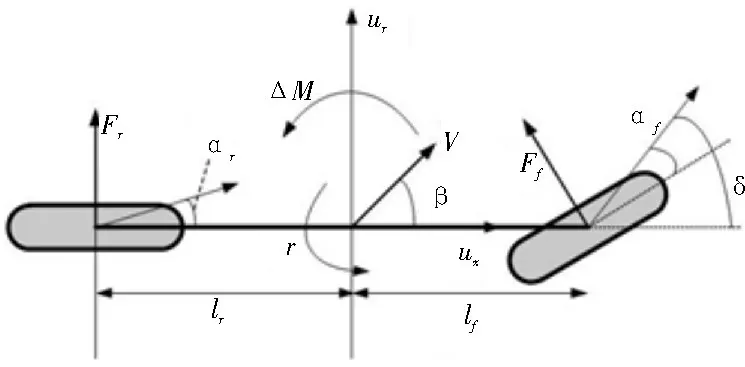
图1 车辆二自由度模型

图1 中，lf与lr分别为车辆质心到前、后轴的距离，β为质心侧偏角，r为车辆横摆角速度，ux为车辆纵向速度，uy为车辆横向速度，δ为前轮转角，Ff与Fr分别为前后轴的侧向力，ΔM为附加的车辆横摆力矩，αf、αr分别为前、后轮的侧偏角。

汽车二自由度动力学模型[15]可表示为：

在直接横摆力矩控制中，以前轮转角为控制器输入，直接横摆力矩为输出u=ΔM。定义状态变量x1=β，x2=γ，则二自由度车辆模型状态方程为：

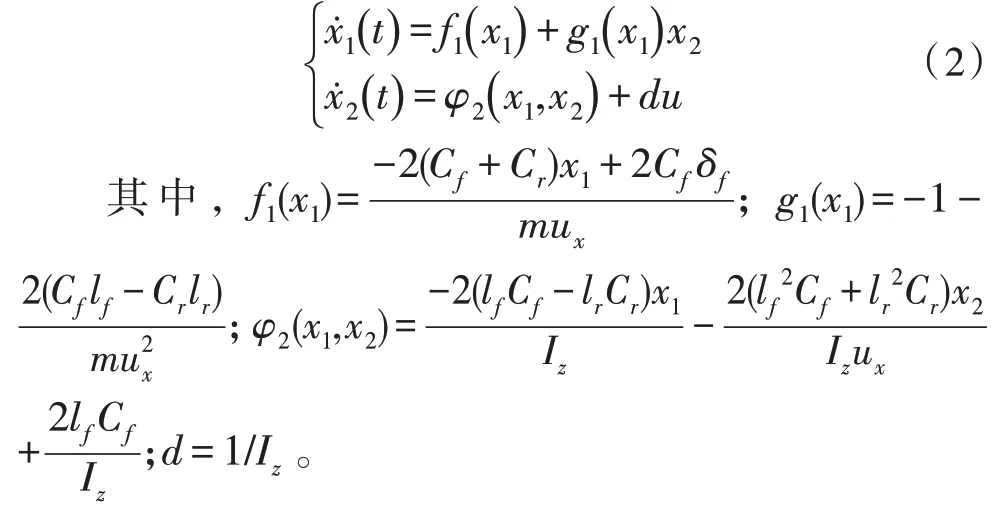
1.2 约束边界模型

由于轮胎存在饱和特性，受地面附着极限的影响，在高速行驶或者紧急转弯时，质心侧偏角过大将导致轮胎无法提供足够的侧向力，产生车轮打滑和汽车甩尾等危险工况出现的可能性。质心侧偏角经验边界值与路面附着系数有关，因此需要对质心侧偏角限制在约束条件内，质心侧偏角经验边界值为2°[14]。

对于车辆横摆角速度而言，必须受到路面附着条件的限制，在轮胎附着极限下侧向加速度必须满足如下约束[14]：

其中，ay为侧向加速度，u为路面附着系数，g为重力加速度。

在车辆质心侧偏角较小时，近似可得：

所以，车辆的横摆角速度应该满足如下条件：

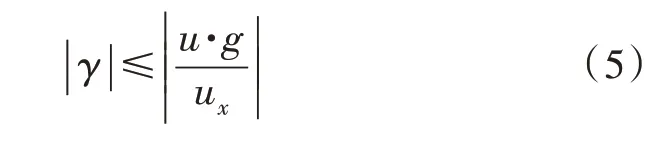
2 全约束BLF控制器设计

在该小节中，将质心侧偏角和横摆角速度的约束应用到控制器设计过程中，采用的设计如下：

第一步：设定质心侧偏角跟踪误差z1=x1-x1d和横摆角速度跟踪误差z2=x2-α1，其中，x1d是理想质心侧偏角，α1是虚拟控制量。

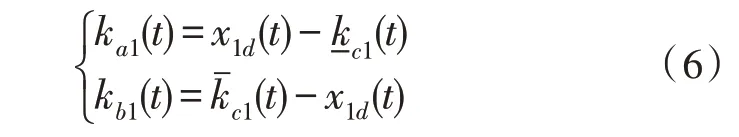
选取非对称BLF 函数：

第二步：由于横摆角速度跟踪误差z2需要被约束，因此选取如下BLF 函数：

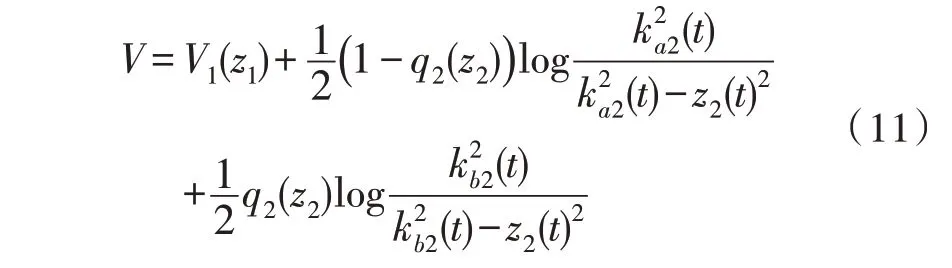
其中，ka2是横摆角速度跟踪误差z2的下约束边界，kb2是跟踪误差z2的上约束边界；q2(z2)=

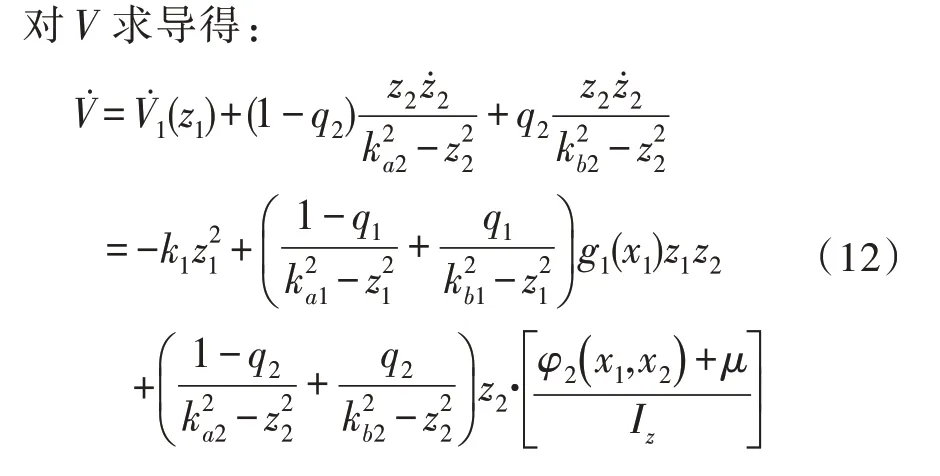
考虑横摆角速度约束边界，设计直接横摆力矩全约束BLF 控制器输出μ为：

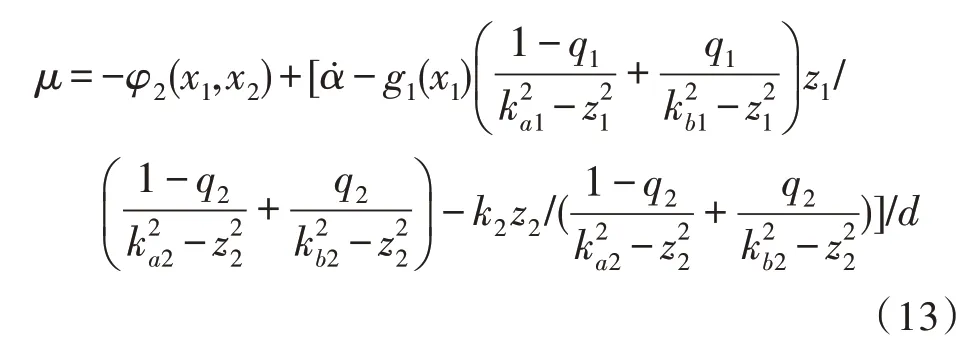
其中，k2是大于0的常数，中间部分的最后一项被用来抵消第一步中式（10）的冗余项g1(x1)z1z2。

将式（13）代入式（12）得：

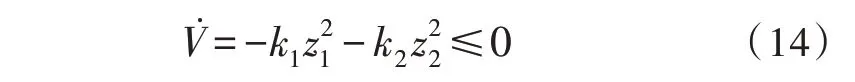
根据式（14）可知，为负。因此，系统是稳定的。基于Barbalat 引理[16]可知，z1、z2有界，在有限时间内趋近于零，即z1→0，z2→0，并且质心侧偏角和横摆角速度始终被约束在其稳定区域内。

3 仿真分析

利用Matlab/Simulink 软件进行数值仿真，根据ISO/TR3888 标准设置双移线试验工况。

车辆主要参数如表1 所示。

表1 车辆主要参数

设置车辆纵向速度ux为30 m/s，路面附着系数为0.6。控制器参数设置如下：k1=32，k2=32，质心侧偏角边界约束的下边界为上边界为横摆角速度约束的下边界为-ug/ux=-0.2rad/s，上边界为理想的质心侧偏角x1d为0。

仿真结果如图2-4 所示。具体来说，图2 给出了方向盘转角输入变化情况。图3 和图4 分别为BLF控制器和无控制下质心侧偏角和横摆角速度的变化曲线。

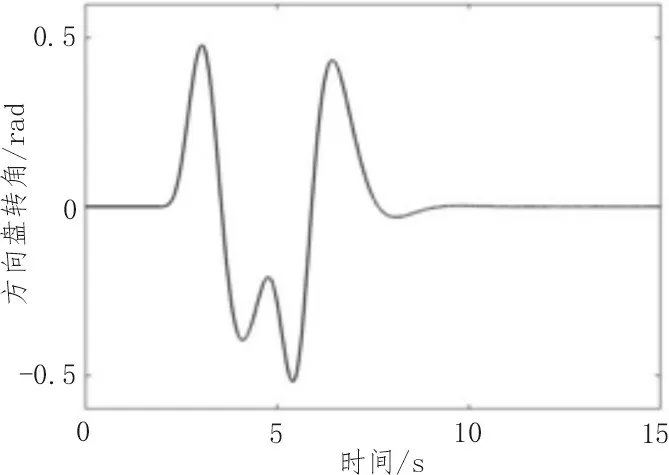
图2 方向盘转角输入

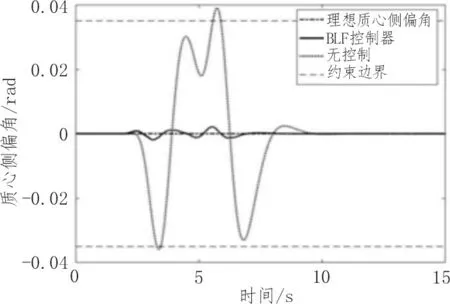
图3 质心侧偏角变化曲线

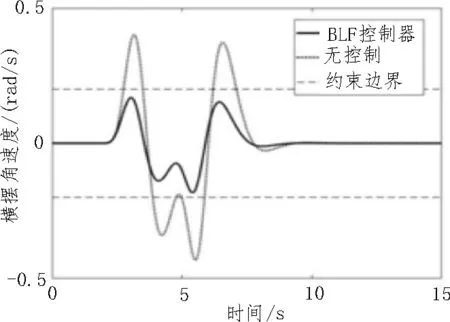
图4 横摆角速度变化曲线

图2 所示为方向盘随时间变化的情况，方向盘输入为标准的双移线输入工况。从图3 可以看出，在BLF 控制器控制下，质心侧偏角可跟踪其理想的质心侧偏角，且在方向盘回正过程中车辆的质心侧偏角没有违反其约束边界-0.035～0.035 rad，而无控制下的车辆质心侧偏角变化在方向盘转向幅度较大时违反了安全稳定区域-0.035～0.035 rad 内，说明此时车辆已经产生失稳的可能。从图4 可以看出，在无控制器参与过程中，横摆角速度在方向盘转角较大时违反了约束边界-0.2～0.2 rad/s，此时车辆存在转向失控的可能性，而在BLF 控制器下，横摆角速度在整个控制过程中始终约束在稳定区域-0.2～0.2 rad/s内，极大地提高了车辆的行驶稳定性[17-18]。

4 结论

该文以汽车理想二自由度模型为对象，针对以往DYC 控制中车辆状态量质心侧偏角和横摆角速度不能严格约束在其稳定区间的问题，基于BLF 函数算法设计了全状态约束DYC 控制器，将质心侧偏角和横摆角速度的边界同时引入控制器的设计过程，严格保证了在车辆行驶过程中质心侧偏角和横摆角速度始终处于安全稳定区域内，从根本上避免了由于质心侧偏角和横摆角速度过大而发生车辆甩尾等危险工况发生的可能性。通过Matlab/Simulink仿真验证了BLF 控制器的控制效果，BLF 控制器可以更好地实现对理想质心侧偏角的误差跟踪控制，并保证在整个控制过程中质心侧偏角和横摆角速度均不会违反约束边界，提高了车辆的横向稳定性。