连续双层缺陷海底管道剩余强度有限元分析
2022-08-17王豪巍
王豪巍
(中海石油技术检测有限公司管道勘察作业部,天津 300450)
0 引言
海底管道在运输石油和天然气时,腐蚀易导致管道失效[1-2],管道的腐蚀缺陷通常表现为不规则形状,从缺陷的剖面来看,缺陷在不同位置具有不同尺寸。目前,腐蚀评价规范ASME B31G—2012[3]、DNVGL-RP-F101[4]等,通常忽略多个腐蚀缺陷对管道剩余强度的影响,将多缺陷近似为单缺陷进行计算,可能造成不必要的管道维修和更换,导致资源的浪费。因此,对双层乃至多层腐蚀缺陷与管道剩余强度的关系进行研究很有必要。本文采用非线性有限元的方法,建立连续双层腐蚀缺陷模型,分析不同尺寸的连续双层腐蚀缺陷对管道剩余强度的影响。
1 非线性有限元分析
1.1 失效准则
非线性有限元中,管道极限内压荷载的确定采用基于Von Mises等效应力的失效判据,该等效应力的计算公式为
式中:σ1、σ2、σ3为3个主应力;σ1≥σ2≥σ3。
根据等效应力判断管道是否失效时,有弹性极限准则、塑性极限状态准则、塑性准则[5-7],其中,弹性极限准则和塑性极限状态准则较保守,而塑性准则考虑了材料的硬化效应,更符合材料特征。因此,在分析中采用塑性准则,即失效时缺陷处沿厚度方向各点均达到极限抗拉强度。
1.2 非线性有限元模型验证
使用ANSYS软件,对文献[8]中的爆破实验进行有限元模拟,实验使用的管道钢型号为X80,管道外径458.8 mm,厚度8.1 mm,弹性模量200 GPa,屈服强度534.1 MPa,极限强度718.2 MPa,泊松比为0.3。有限元模拟使用Ramberg-Osgood应力应变模型[9-10],其公式如下:
式中:σ为应力,MPa;σu为极限抗拉强度,MPa;E为弹性模量,MPa;ε为应变。
根据实验情况,建立有限元模型进行计算,计算时管道只承受内压荷载,考虑材料非线性和几何非线性[11],当沿管道厚度方向的等效应力均达到σu时,判定管道失效,得到计算的有限元模拟结果与实验结果比较见表1。表中误差δ=|(PF-PT)/PT|×100%。
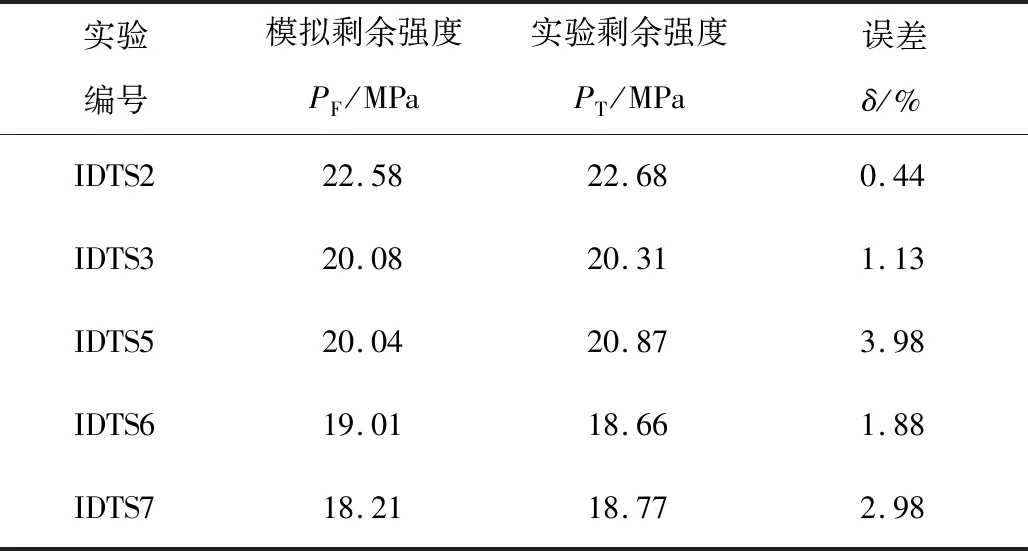
表1 实验结果与模拟结果对比
由表1可知,模拟结果和实验结果的误差均在4%以内。图1为有限元模拟的部分失效形态结果,图中深色区域应力达到极限抗拉强度σu,将图1有限元模拟管道失效时的最大应力分布位置,与文献[8]中的实验破坏位置对比后,发现二者吻合程度较高。由以上两点,可以证明使用该分析方法计算管道剩余强度的准确性。

(a)IDTS5
2 管道有限元模型及计算结果分析
2.1 连续双层缺陷管道有限元模型
文中研究X80钢管道,材料参数与1.2节相同,模型长度为1 600 mm。连续双层缺陷分为上、下两层,且都为矩形,上层缺陷的长度为lT,宽度为wT,深度为tT;下层缺陷的长度为lB,宽度为wB,深度为tB;宽度wT和wB为缺陷圆心角度,如图2所示。
2.2 连续双层腐蚀轴向分布
2.2.1 上层腐蚀长度lT变化
图3为管道剩余强度随上下层缺陷长度比lT/lB变化的曲线,此时缺陷的宽度和深度不变,下层缺陷wB=8°,tB=5 mm,上层缺陷wT=4°,tT=2.5 mm。由图3可知,管道剩余强度随lT/lB的增大逐渐降低;当下层缺陷长度lB增大,相同lT/lB下的管道剩余强度降低;在下层缺陷长度lB不同的情况下,剩余强度随lT/lB变化的曲线呈现出了相同的趋势,当lT/lB处于0.2~0.7范围内时,剩余强度具有对数变化特征,但总体接近线性变化。
2.2.2 上层腐蚀宽度wT变化
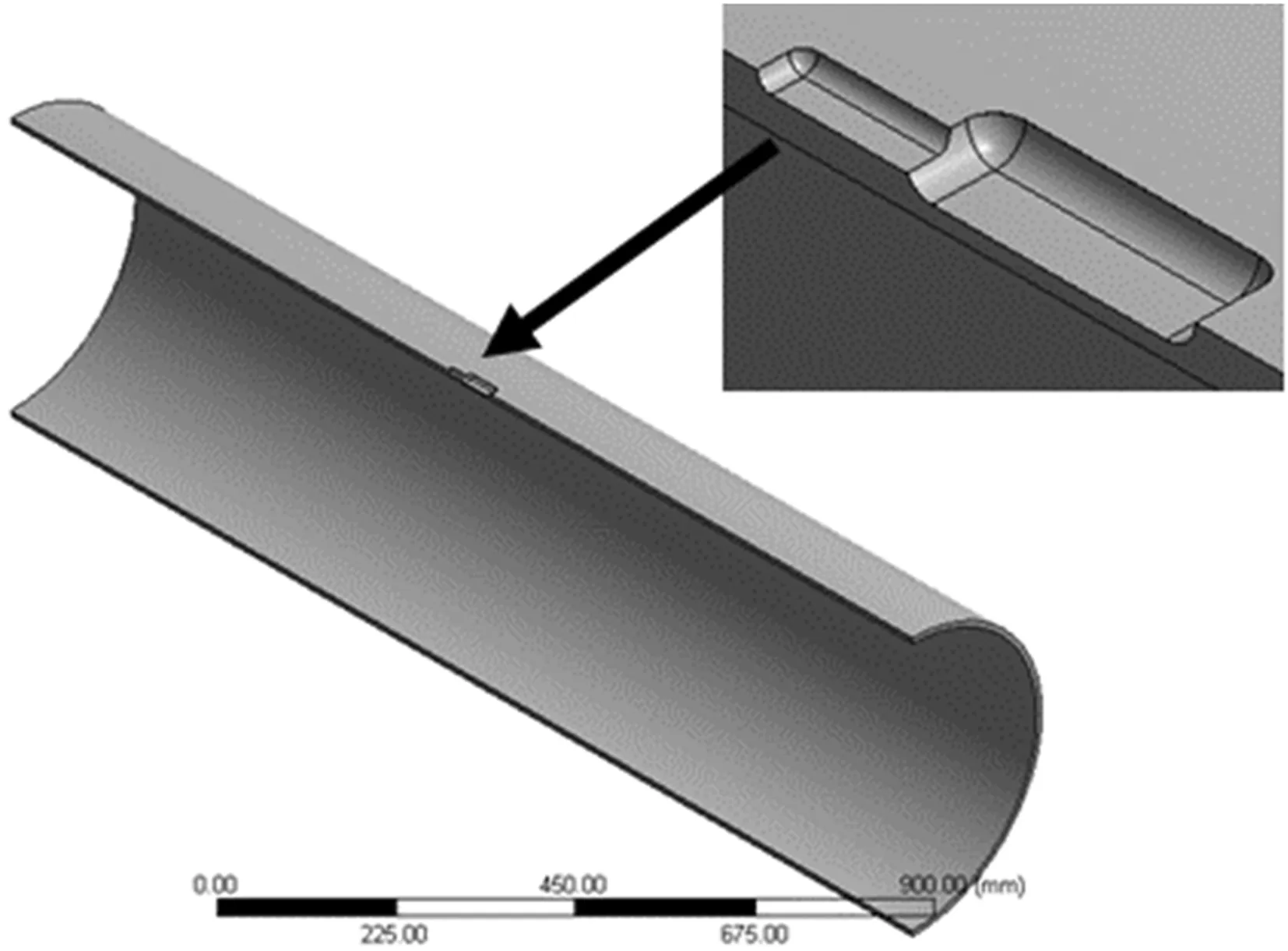
(a)连续双层缺陷轴向分布
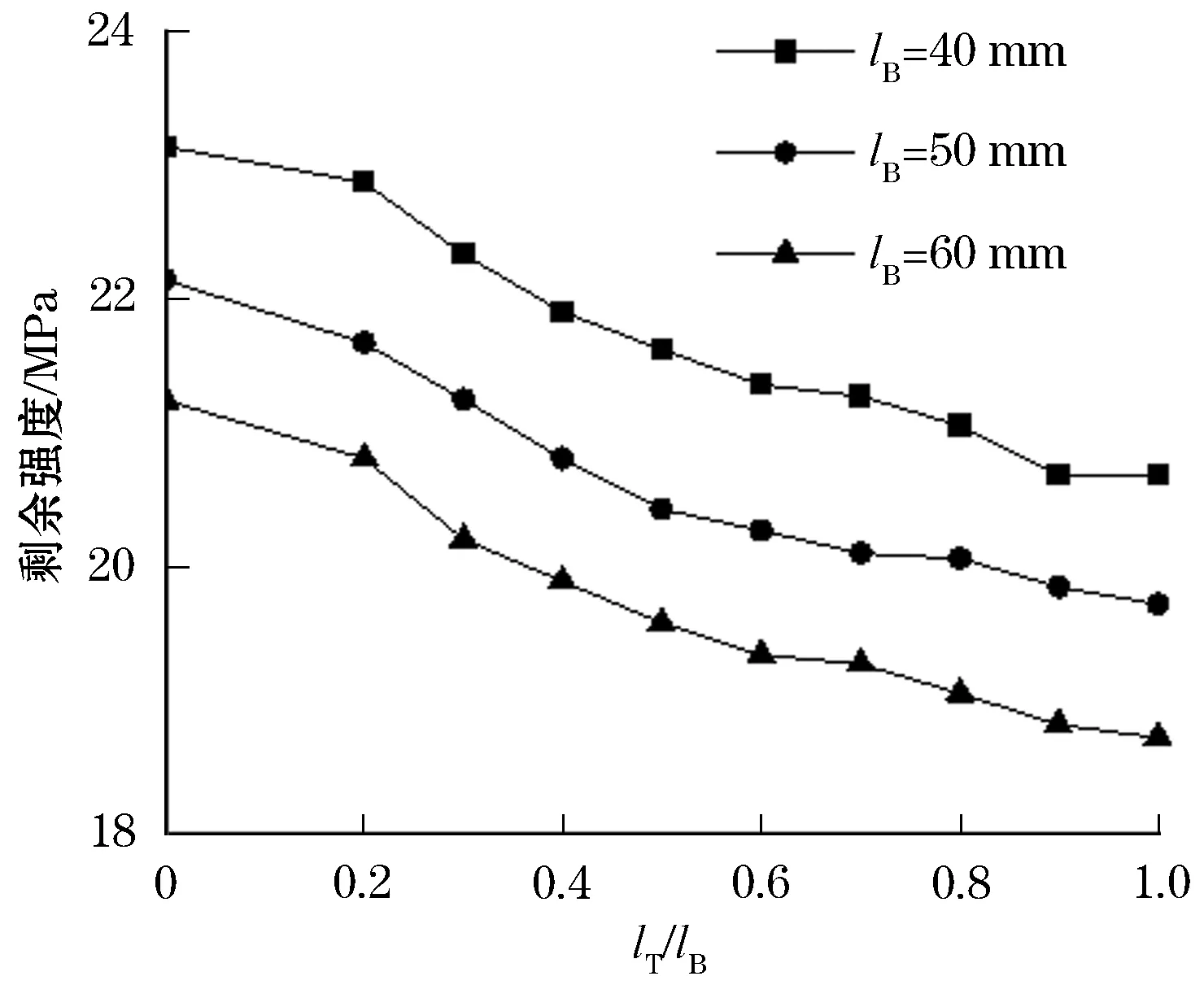
图3 剩余强度与长度比变化曲线
图4(a)为管道剩余强度随wT/wB的变化曲线,此时缺陷长度和深度不变,下层缺陷lB=50 mm,tB=5 mm,上层缺陷lT=25 mm,tT=2.5 mm。在底层缺陷宽度wB不同的情况下,管道剩余强度与wT/wB的变化曲线具有相似的变化趋势。将横坐标变为上层缺陷宽度wT,得到图4(b)的变化曲线。由图4(b)可知,不同wB下,剩余强度的变化曲线吻合程度较高,当wT<4°时,剩余强度下降迅速,具有明显的线性变化趋势;当wT>4°时,管道剩余强度先增加后降低。

(a)
2.2.3 上层腐蚀深度tT变化
图5为管道剩余强度与tT/tB的关系曲线,此时缺陷长度和宽度不变,下层缺陷lB=50 mm,wB=12°,上层缺陷lT=25 mm,wT=6°。由图5可知,剩余强度随着tT/tB的增加而减小;下层缺陷tB越大,相同tT/tB下的剩余强度越小;当tT/tB<0.5时,管道剩余强度下降较慢,不同tB下的剩余强度有近似的变化趋势;当tT/tB>0.5时,管道剩余强度下降较快,下层缺陷深度tB越大,曲线斜率越大,tT/tB的改变对管道剩余强度的影响越大,同时2个阶段的剩余强度变化均为线性趋势。对比缺陷长度和宽度影响下的管道剩余强度变化情况,可知缺陷深度的变化是影响剩余强度的主要因素。

图5 剩余强度变化曲线
2.3 连续双层腐蚀环向分布
当上下层缺陷沿管道环向分布时,为了研究上层缺陷的长度、宽度、深度对管道剩余强度的影响,设计以下3种工况:
(1)上下层缺陷长度比变化,此时缺陷尺寸wT/wB=4°/8°,tT/tB=2.5 mm/5 mm。
(2)上下层缺陷宽度比变化,此时缺陷尺寸lT/lB=30 mm/60 mm,tT/tB=3 mm/6 mm。
(3)上下层缺陷深度比变化,此时缺陷尺寸wT/wB=5°/10°,lT/lB=25 mm/50 mm。
图6为环向分布情况下,管道剩余强度和上下层缺陷长度比lT/lB、宽度比wT/wB、深度比tT/tB的变化关系,在环向双层腐蚀缺陷中,上层缺陷长度、宽度、深度的变化对管道剩余强度产生影响较小。
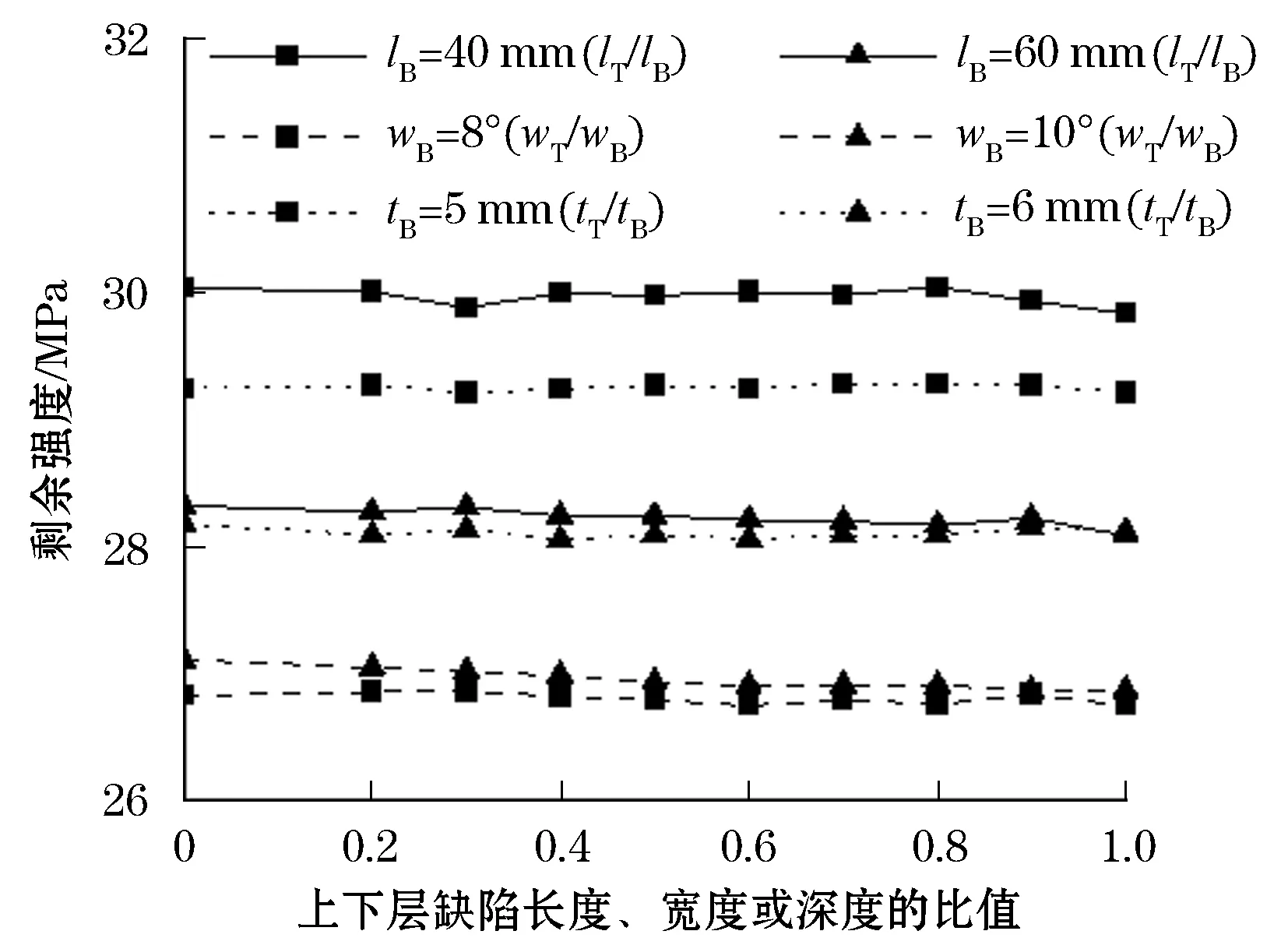
图6 不同尺寸剩余强度变化曲线
3 评价方法分析
分别使用ASME B31G—2012方法和DNVGL-RP-F101方法(DNVGL考虑模型系数0.9)计算连续双层缺陷轴向分布情况下的管道剩余强度,计算结果与有限元结果的误差分布如图7所示,计算误差=(有限元模拟结果-评价方法计算结果)/有限元模拟结果。
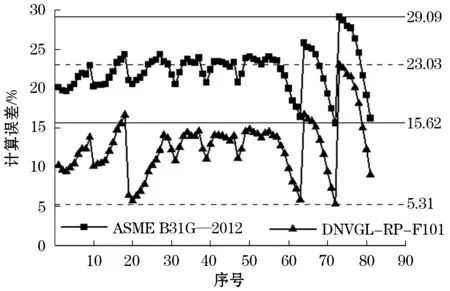
图7 剩余强度评价方法对比
在计算管道剩余强度时,ASME B31G—2012方法和DNVGL-RP-F101方法均将连续双层腐蚀缺陷视作单个缺陷进行计算,公式中缺陷长度为连续双层缺陷总长,缺陷深度为连续双层缺陷中最大深度,因此产生了一定的保守性。图7中,使用ASME B31G—2012方法的结果误差分布在15.62%~29.09%之间,均大于15%,使用DNVGL-RP-F101方法的结果误差主要分布在5.31%~23.03%之间。因此,对于该种类型管道剩余强度的计算,使用DNVGL-RP-F101方法的计算结果准确程度明显高于使用ASME B31G—2012方法的计算结果,使用ASME B31G—2012方法更保守。
4 结论
对于轴向分布的连续双层腐蚀缺陷管道,上层较小尺寸缺陷的出现,对下层缺陷单独存在情况下的腐蚀管道剩余强度的影响具有规律性。上下层缺陷长度比增大,管道剩余强度降低;在上层缺陷宽度圆心角小于4°时,剩余强度随上层缺陷宽度的增大线性减小;上层缺陷宽度圆心角大于4°时,剩余强度随上层缺陷宽度的增大先增加后减小;上下层缺陷深度比增大时,剩余强度降低较快,深度变化对剩余强度影响较大。
在连续双层腐蚀缺陷沿环向分布的情况下,改变上下层缺陷长度比lT/lB、宽度比wT/wB、深度比tT/tB,对管道失效压力影响较小,与下层缺陷单独存在时(lT/lB、wT/wB、tT/tB为0)的管道剩余强度结果相近,因此可以根据单腐蚀管道计算方法进行计算。
使用DNVGL-RP-F101方法计算连续双层缺陷管道的剩余强度,结果更准确,保守性更低,优于ASME B31G—2012方法。
