管道支吊架布置优化方法

贾占举，刘文磊，杨静洁，杨辉青，沈 聪，范继珩，朱 鑫，严佳兵

(中国核动力研究设计院，四川成都 610005)

0 引言

在对放射性废物处理系统管道进行设计时，要满足日常的输送要求，还要考虑管道附件的受力状况，从而使整个管道系统处于安全运行的状态。管道支吊架是管道系统的重要组成部分,具有承受荷载、限制位移和控制振动等作用。设计中, 合理布置支吊架位置, 是降低管道应力和支吊架载荷的有效途径[1]。

在传统的放射性废物处理系统管道布置设计过程中，设计人员通常根据规范要求和布置经验完成支吊架的布置，并总结了一系列管道布置和优化设计方法[2-3]。闵琪等[4]用管道有限元方法对高温气冷堆反应堆压力容器承重支承的冷却系统进行了管道应力分析，提出了管道支吊架布置的优化方案。王新军等[5]提出一种包含力学分析过程、特殊应力指数的计算方法和计算结果评定的方法，以尽可能减少管道调整和协调次数。李彦萍[6]利用CAESAR Ⅱ软件和GLIF软件对霍州电厂主蒸汽管道应力分析及优化设计。但这些方法通常需要大量的人工试算来完成，且最终很难得到最优的布置方案来获得最大的应力裕度[7]。

为了解决管道人工优化布置中存在的问题，提出了一种放射性废物处理系统管道支吊架优化布置方法。基于ANASYS软件和APDL语言建立了相应管路参数化的有限元模型，以管道应力为优化目标，建立了一种管道优化布置方法并验证了计算方法的有效性。

1 计算方法

本文提出的方法是基于有限单元法(FEM)对支吊架位置进行不断迭代优化，最终达到管路应力最小的目的，其流程如图1所示。

图1 优化方法流程图

1.1 参数化模型

优化计算的前提是完成管路模型的参数化，为提高计算效率，需要进行模型简化。对于管道，其特征是截面一定且法向和径向尺寸相差很大，由于六面体网格长细比限制，会使网格数量非常多，在工程上通常将其简化为三维梁单元。三维梁单元本质是线单元，全部行为依靠端点位移决定，主要关注其弯曲变形。对于阀门等几何形状复杂的管件，将其简化为有集中质量的梁单元。

本文采用ANSYS软件的Piping Models模块基于APDL语言完成参数化模型构建。Piping Models模块基于一维单元进行模型构建和计算，该单元使用户按规范的管路输入数据建立管路系统模型，不必按照标准的ANSYS直接生成方法进行建模操作。当输入管路命令，ANSYS程序内部将管路数据转换成直接生成模型的数据，并将转换的信息存到数据库里。

用管路命令建立管路系统模型进行分析，通过3个主要步骤完成，即建立基本的管路数据、定义管路系统的几何形状和约束施加。管路的几何形状是利用直管单元(PIPE16)和弯管单元(PIPE18)生成管路网络的线模型。节点和单元的几何形状是以延伸长度的增量和弯曲半径来定义。

1.2 优化数学模型

管道支吊架布置优化目标是在满足相关规范的条件下，通过调整支吊架位置，使整个管路有更大的应力裕度。因此，优化设计目标函数f(X)为最小管道应力，支吊架位置为优化变量。一般地，支吊架布置需满足GB 50242—2002 《建筑给水排水及采暖工程施工质量验收规范》[8]相应规定，将其作为约束条件，即得到管道支吊架布置优化设计的数学模型。

1.3 优化算法

文中的优化算法是全局扫描算法和零阶优化的组合算法。ANSYS软件提供2种优化方法，零阶优化方法和一阶优化方法[9]。零阶优化方法即序列无约束极小化方法(SUMT)，如式(1)所示，通过对目标函数添加罚函数，将问题转化为非约束的优化问题，再用曲线拟合建立目标函数和设计变量之间的关系来进行逼近，每次优化循环生成一个新的数据点，是工程上常用的方法。

(1)

对于一阶优化方法，在迭代中，通过梯度计算(最快速下降法或共轭梯度法)确定其搜索方向，并用线性搜索法对非约束问题进行最小化。每次迭代涉及多次分析 (对分析文件的多次循环)，以确定适当的搜索方向，因为一阶优化方法计算中无近似，因此计算精度很高，如式(2)所示。

(2)

工程上因施工条件限制，对于计算精度要求不高且需要很高的计算效率，因此采用零阶方法。考虑到设计初值对零阶优化方法的计算精度和速度的影响，在优化前先采用全局扫描算法，对目标函数的整体变化进行评估，并为零阶优化提供合理的初值。

1.4 优化结果核算

现实情况中，由于泵、往复压缩机等运转时管道内呈脉动状流动，这种脉动的流体在管道内形成脉动液压，使相连的管道系统产生机械振动，振动是这类管道设备中必须考虑的问题。

文中以有限单元法为基础进行优化分析，考虑冷态装配和热态工作时的载荷进行静态计算，对于泵、往复压缩机等振动部件以其最大振幅进行分析。振动计算涉及动力学分析，与静力分析计算方法内核不同，当前分析未将其整合至一体，因此在优化结束后开展进一步动力学核算，并用变量影响因子对结果进行修正，得到最终优化设计结果。

2 实例计算

文中使用了一个典型的管路模型对计算方法进行介绍，并使用全面正交试验方法，采用CAESAR II软件作对比分析，验证了计算方法的有效性。

2.1 管路物理模型

管道三维布置如图2所示。管路输送介质为高温除盐水，密度0.999 g/cm3，设计温度100 ℃，设计压力0.2 MPa。

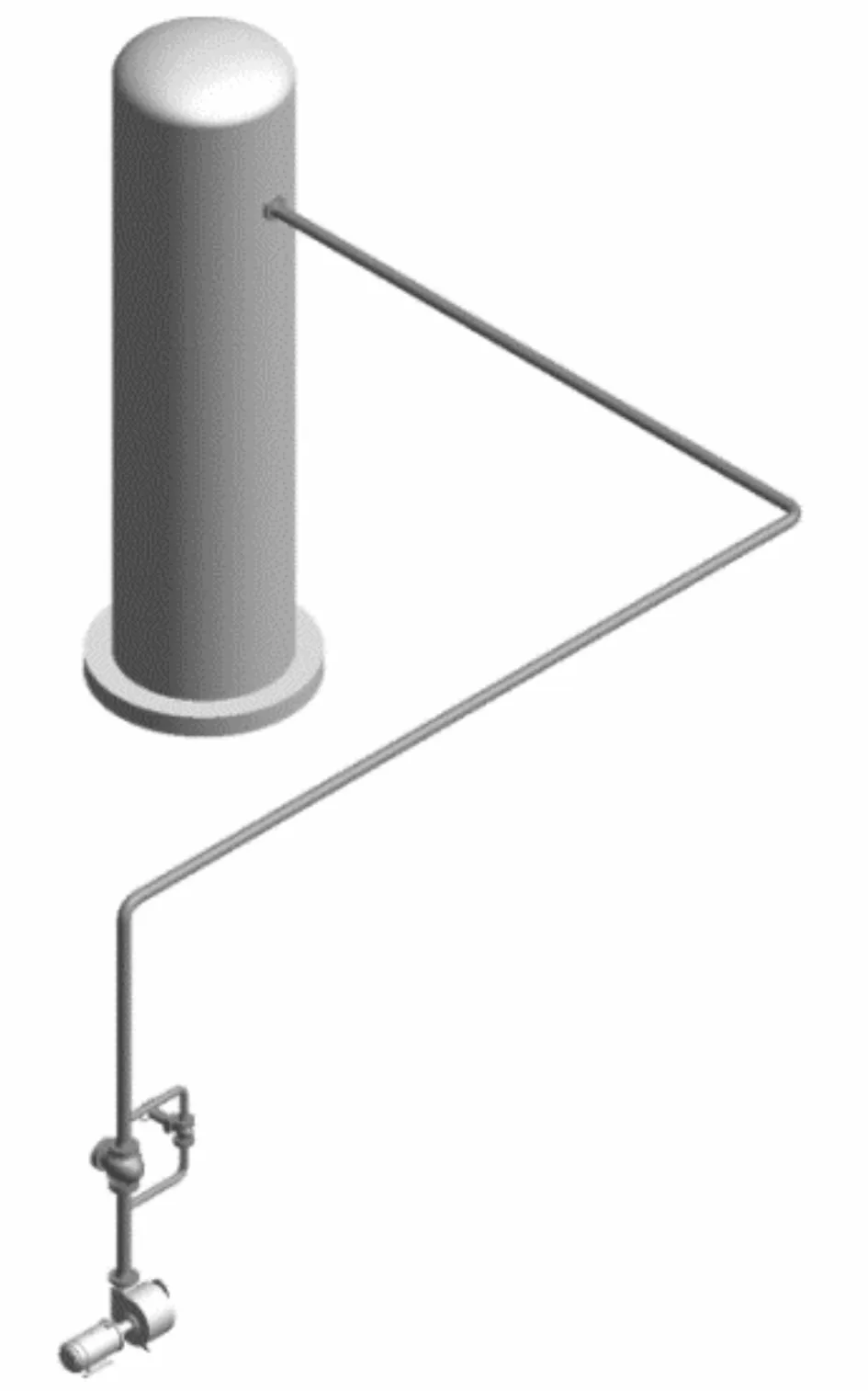
图2 管道三维布置图

管路包含贮槽、水泵、不锈钢机制弯头、异径三通、止回阀、球阀、无缝不锈钢管等，其主要特性及数量如表1所示。

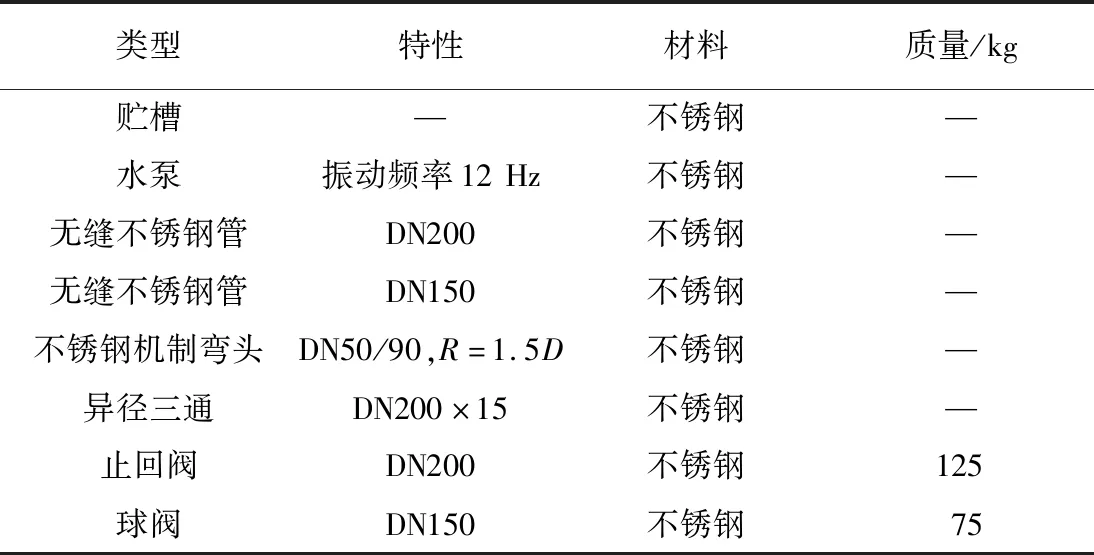
表1 管路模型设备及材料

2.2 管道参数化模型

管路材料均为不锈钢，规格为Φ219×6(DN200)和Φ159×4(DN150)。管道的载荷为管道自重及热态载荷。约束条件施加包括管道入口出口及支吊架位置约束，入口约束考虑泵工作振动，出口约束考虑贮槽的热胀，支吊架类型为支撑支架，管路特性条件如表2所示，建立模型如图3所示。2个支吊架位置分别为L1和L2。

图3 ANSYS管道有限元模型

表2 管路特性条件

2.3 模型验证

采用管道应力分析软件CAESAR II对所构建的有限元模型进行验证。建立相同的管道模型进行分析，如图4所示。

图4 CAESAR II管道有限元模型

2.3.1 验证方法

验证方法为全面正交试验，支吊架1位置为因素A，划分为4个水平，分别为2 000、3 000、4 000、5 000 mm，支吊架2位置为因素B，划分为3个水平，分别为2 000、3 000、4 000 mm，试验表如表3所示。

表3 试验数据表 mm

2.3.2 结果分析

在ANSYS和CAESAR II中分别对表3中各项进行计算，应力结果如图5所示，应力差分布如图6所示。

图5 应力计算结果对比

图6 应力差分布

由试验结果可知，ANYSY与CAESAR II应力计算结果的增减具有一致性，且ANSYS计算结果均略大于CAESAR II计算结果，这可能是由于软件计算方法不同导致的。平均应力差2 243 kPa，最大应力差为3 251 kPa，差值率2.3%，发生在试验8处，且由图6可知，应力差分布具有一定规律性。

对应力差最大点处应力云图进行对比，如图7所示，数值单位为kPa。2种软件计算结果的应力分布是一致的，最大应力均发生于支吊架1位置处。

2种软件计算结果从应力大小、分布以及差值对比表明，有限元模型构建合理，计算结果具有可信度。

(a)ANSYS应力分析云图

2.4 支吊架位置优化

2.4.1 优化数学模型

管道支吊架布置优化设计的数学模型为：

(3)

2.4.2 优化结果及分析

设计优化变量优化前后对比如表4所示。经验值虽能满足相关规范及应力要求，但并不能获得最大应力裕度，而优化后的管道最大应力相对经验值下降了29.7%，管道安全性更好。

表4 设计优化变量优化前后对比

通过分析得到了设计变量对管道应力的影响曲线，如图8所示。横坐标表示设计变量在变化范围内的等分点，纵坐标表示对目标函数的影响值，影响值越大则管道应力越大。得到的支吊架位置变化对于管道应力的影响，可在后续管道布置中提供参考。

图8 设计变量对管道应力的影响

2.4.3 优化结果核算

管道的流体脉动频率与管道自身固有振动频率相等时，就会出现共振，从而破坏管道。支吊架对于管道的约束极大地影响管道固有频率，因此需要对布置后的管道振动频率进行核算。计算得到优化后位置前10阶频率如表5所示，前4阶振型如图9所示。

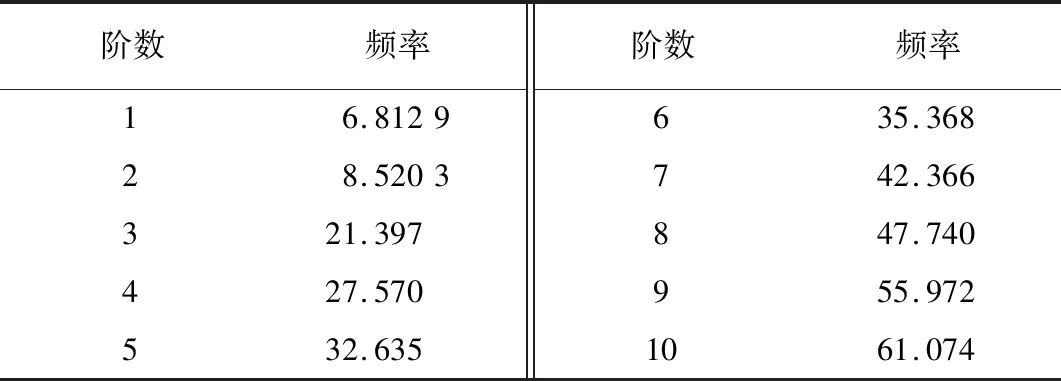
表5 管道固有频率 Hz

水泵振动频率为12 Hz，处于管路系统二阶与三阶频率之间，不会产生共振，系统安全可靠。

3 结论

本文基于FEM提出了一种管道支吊架布置优化方法，结论如下：

(1)建立相应管路参数化的有限元模型，以管道应力为优化目标，以GB 50242—2002为约束条件，采用全局扫描及零阶优化的组合算法确定支吊架最优位置，得到优化设计结果。

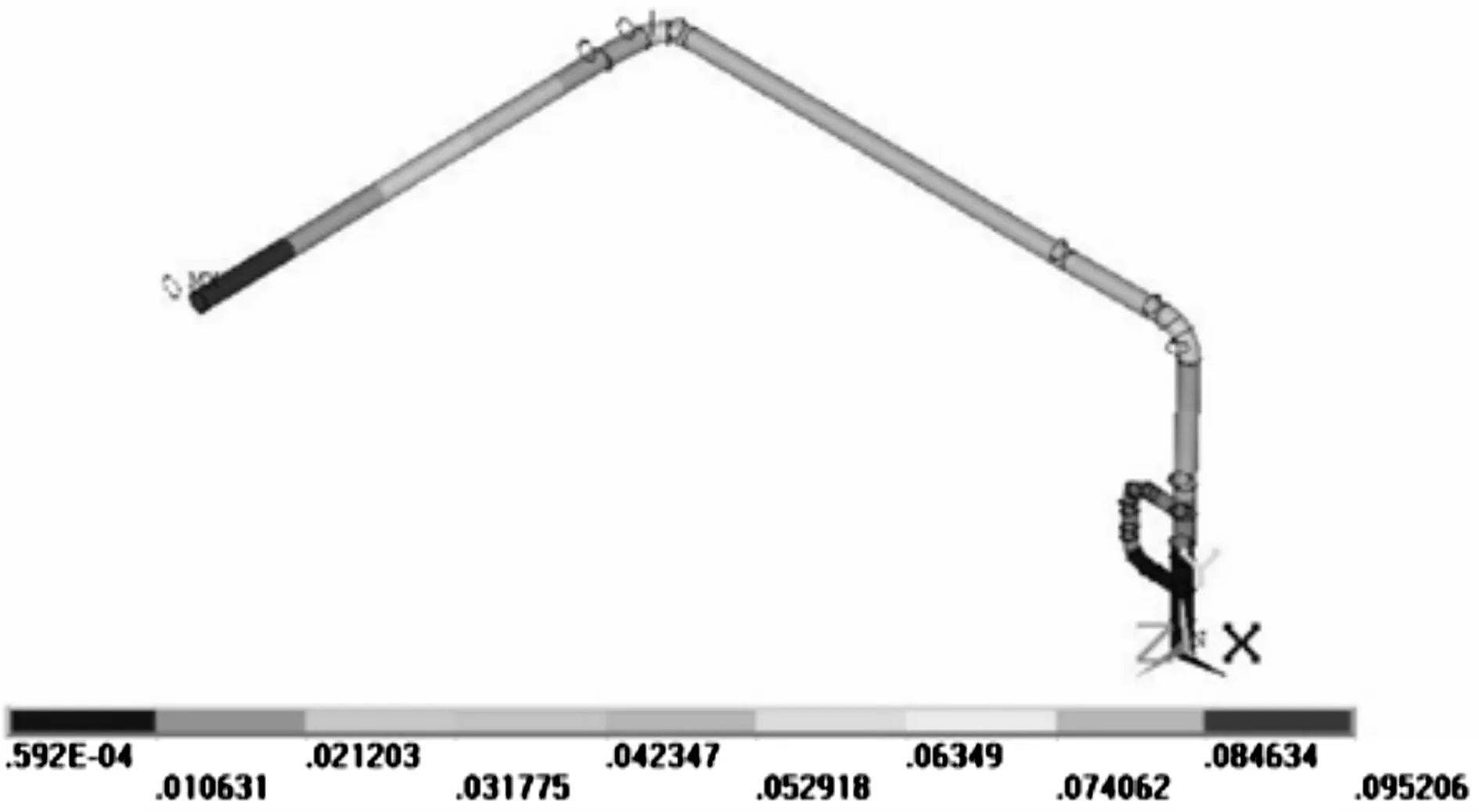
(a)一阶振型

(2)算例中采用全面正交试验方法，使用CAESAR II软件作对比分析，验证了所建的管路有限元模型的正确性。

(3)文中方法避免了在管道布置过程中大量的人工试算，并能够获得最大应力裕度，系统安全性能得到提升。