浮式风机气动—水动—气弹性耦合响应数值模拟
2022-08-17赵伟文万德成
黄 扬,赵伟文,万德成, 2
(1.上海交通大学 船海计算水动力学研究中心(CMHL)船舶海洋与建筑工程学院,上海 200240;2.浙江大学 海洋学院,浙江 舟山 316021)
相较于陆上风电场,海上风电场不占用宝贵的土地资源,受到的空间限制较小,且能避免噪音污染和视觉干扰对人类活动的影响。同时,海上风能的质量更高,风速更加平稳,发电效率更高,因此海上风电场逐渐成为风能开发的主要趋势[1]。近年来,随着风电产业的快速发展,风力发电逐渐从近海走向远海。随着风机工作水深的增加,固定式海上风力机的成本急剧增大。相较而言,采用漂浮式基础的海上风力机的性价比明显提高,这使得浮式风机逐渐从概念设计走向工程应用[2]。为了降低风电场的建设和运行成本,海上风力机逐渐向大型化方向发展,风力机的装机容量不断增大,对应的风力机叶片尺寸也显著增加[3]。大型浮式风机成为未来深远海优质风能开发的重要方式和研究热点。
浮式风机是由风力机、浮式支撑平台以及系泊系统组成的复杂海洋结构物系统。在风—浪—流载荷的作用下,风力机的气动载荷和浮式支撑平台的水动力响应之间存在显著的相互干扰作用,使得浮式风机的气动—水动耦合响应呈现出明显的非稳态特性[4]。此外,风力机大型化使得叶片细、长、薄的特点愈发突出。随着叶片尺寸的增加,叶片柔性变形越来越显著,进而会对浮式风机的耦合性能产生不利影响[5]。这些因素使得浮式风机推广应用还存在较大的挑战。为了加深对大型浮式风机在风浪联合作用下耦合响应特性的认识,需要针对浮式风机的气动—水动—气弹性耦合响应特性开展相关研究,并进一步为浮式风机的优化设计提供参考建议。
模型试验是研究浮式风机耦合响应特性的可靠手段,但受限于试验场地和设备,试验结果不可避免地会受到尺度效应以及低雷诺数的影响,进而会影响试验结果的适用范围[6]。为了获得更加可靠的浮式风机的运行数据,海外风电巨头开展了相关的浮式风机实测项目,如挪威国家石油公司的Hywind项目[7]、Principal Power在葡萄牙的WindFloat半潜式浮式风机实测项目[8]等。尽管实测数据的价值很高,但浮式风机实测试验的成本和风险也十分巨大。相较而言,数值方法通过对浮式风机系统的各个部分进行数值建模分析,可以获得实尺度浮式风机的耦合动力响应特性,具有时间短、成本低、精度高的特点,因此被广泛地应用于浮式风机耦合性能的研究。浮式风机气动—水动—气弹性耦合响应数值模拟涉及到风力机的气动性能、浮式平台及系泊系统的水动力性能以及叶片结构变形响应之间的复杂相互作用。为了简化计算,一些学者提出采用叶素动量理论(blade element momentum,简称BEM)或者涡尾迹方法(wake vortex method,简称WVM)来计算风力机的气动性能,并结合Morison公式或者势流理论预报浮式支撑平台的水动力响应。同时,基于等效梁理论求解叶片结构变形响应,从而建立了浮式风机气动—水动—气弹性耦合响应计算模型,并开发出一系列浮式风机耦合性能分析软件,如FAST[9]、HAWC2[10]等。尽管这些耦合分析软件具有计算快速的优势,但其对复杂入流工况条件下浮式风机的耦合响应问题的适用性较差。随着的计算机技术和计算能力的快速发展,计算流体力学(computational fluid dynamics,简称CFD)方法因其适用范围广、计算精度高以及数据丰富的特点而被广泛应用于浮式风机在复杂入流工况条件下耦合动力响应特性的数值模拟研究。Tran和Kim等[11]基于STAR-CCM+软件和自主开发程序对半潜式浮式风机在风浪联合作用下的耦合响应特性进行了CFD模拟;Liu等[12]等基于开源软件平台OpenFOAM开发了一套针对浮式风机气动—水动耦合响应的CFD分析工具,并结合MBD(multi-body dynamics)方法求解叶片结构变形。值得注意的是,CFD方法存在对计算资源需求大、计算速度相对较慢的特点。为此,需要进一步地对浮式风机耦合计算模型继续完善,提高计算效率。
为了减少对计算资源的消耗,采用弹性致动线模型来模拟风力机,并基于等效梁理论和一维有限元方法计算叶片结构变形响应,结合两相流CFD求解器naoe-FOAM-SJTU,建立了浮式风机气动—水动—气弹性耦合响应计算模型,实现了风浪联合作用下浮式风机耦合响应的数值模拟。通过对规则波和剪切风作用下Spar型浮式风机的气动—水动—气弹性耦合响应进行数值模拟,探究风力机气动载荷、浮式平台运动响应以及叶片结构变形响应之间的耦合作用,并对浮式风机的尾流场特性进行了分析。
1 浮式风机气动—水动—气弹性耦合计算方法
1.1 风力机气动性能计算模型
致动线模型(actuator line model,简称ALM)[13]是一种模拟风力机气动性能的简化方法。在ALM中,风力机叶片被等间距离散为一系列叶素单元,每个叶素单元被虚拟的致动点代替,然后基于叶素理论计算作用在叶素单元上的气动载荷,并通过高斯核函数将致动点处的气动力投影到流场,模拟风力机的尾流。ALM不需要求解叶片表面的边界层,因此可以极大地减少了计算量。在ALM基础上,提出了一种弹性致动线模型(elastic actuator line model,简称EALM)[14],如图1所示。该模型考虑了平台运动以及叶片变形对风力机气动性能的影响,实现了对大型浮式风机非稳态气动响应特性的模拟。
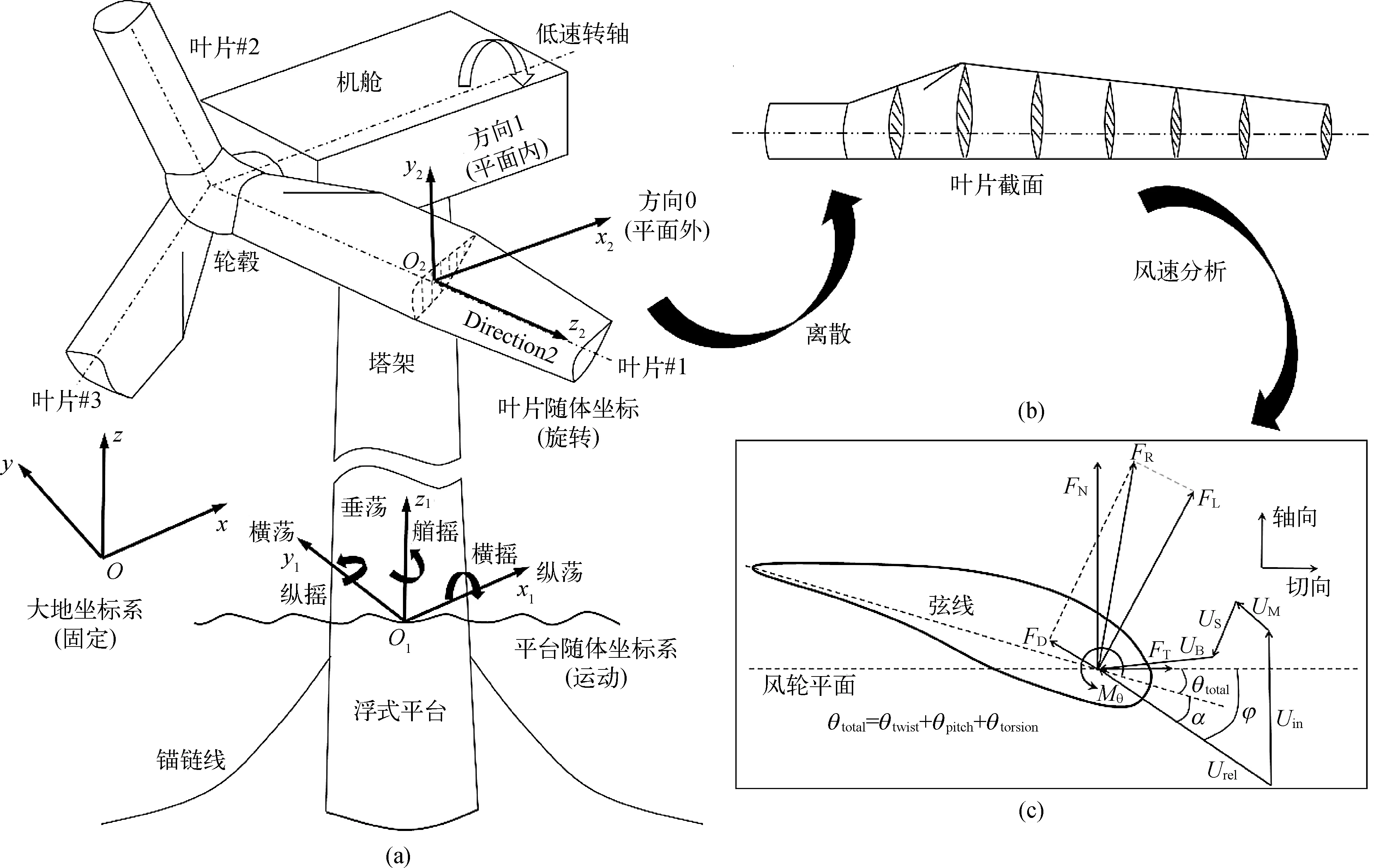
图1 弹性致动线模型原理示意
为了体现平台运动以及叶片变形对风力机气动性能的影响,EALM在风力机叶片截面处的速度矢量分析中引入了由于平台运动导致的附加速度UM和叶片变形引起的附加速度US。因此,叶片截面处的速度矢量Urel可以通过下式进行计算:
Urel=Uin+UB+UM+US
(1)
其中,Uin表示叶片截面处的入流风速,UB=Ω·r表示叶片的旋转速度,Ω是风轮转子的旋转角速度,r代表叶片截面距离叶根的距离。根据叶片截面处的矢量关系,可以得到入流角φ以及叶片截面的局部攻角α:
φ=arctan(Ua/Ut)
(2)
α=φ-θtotal
(3)
θtotal=θpitch+θtwist+θtorsion
(4)
其中,Ua和Ut分别是Urel在叶片随体坐标系下的投影,θpitch代表叶片截面所在位置的桨距角,θtwist为局部扭转角,θtorsion为叶片扭转变形角。根据局部攻角,结合二维翼型的气动性能数据进行插值,可以得到叶片截面处的升力系数CL和阻力系数CD。进一步地,风力机叶片上的气动载荷f可以通过下式进行计算:
(5)
其中,L和D分别表示作用在翼型截面处气动升力和气动阻力,ρ表示空气的密度,c代表翼型截面的弦长,Nb表示风力机叶片的个数,eL和eD分别表示叶片随体坐标下不同方向的单位矢量。
进一步地,计算得到的风力机气动载荷需要通过高斯核函数光顺地投影到叶片周围的流场。投影到流场中的体积力可以通过下式进行计算:
(6)
(7)
其中,ηε代表高斯核函数,d表示网格节点与致动点的距离,ε代表高斯宽度系数,一般取值为风轮叶片附近最小网格尺寸的2倍或者叶片弦长的1/4。
1.2 叶片结构变形响应计算模型
大型浮式风机的叶片具有很大的展弦比,叶片的主要变形是弯曲变形和扭转变形,剪切变形程度较小。因此,可以采用Euler-Bernoulli梁模型对风力机叶片进行简化处理,将之视为一端固定一段自由的悬臂梁,并选用离散参考系的多自由度模型进行计算[15]。
如图2所示,采用一维有限元方法对风力机叶片进行离散,将连续梁结构划分成用有限节点相连接的离散单元体系。每个梁单元包含2个节点,每个节点处包含3个自由度,分别表示叶片的挥舞变形δx,摆振变形δy和扭转变形δθ。根据达朗贝尔原理,可以构建叶片结构变形响应的动力平衡方程:
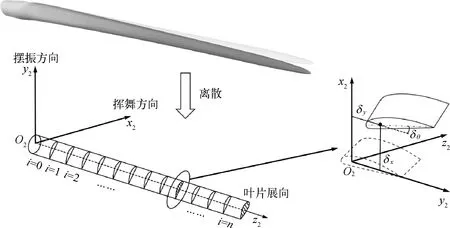
图2 风力机叶片结构计算模型示意
(8)
其中,M、C和K分别代表风机叶片结构离散系统的整体质量矩阵、整体阻尼矩阵和整体刚度矩阵,F表示作用在叶片结构单元上的外载荷向量,y代表节点位置的全自由度向量:
(9)
其中,y1、y2和yθ分别代表全部梁单元节点沿挥舞方向的线位移向量、沿挥舞方向的线位移向量和扭转变形的角位移向量。整体阻尼矩阵C可以通过M和K的线性组会得到:
C=a0M+a1K
(10)
其中,a0和a1是比例系数,由叶片振动的自然频率和阻尼比进行确定:
(11)
其中,ξ代表阻尼比,fn1和fn2分别表示叶片一阶振动自然频率和二阶振动自然频率。
1.3 浮式风机气动—水动—气弹性耦合响应求解
采用两相流CFD求解器naoe-FOAM-SJTU对浮式风机的水动力响应特性进行预报,并采用分段外推法求解系泊系统[16]。进一步地,通过结合EALM和叶片结构变形计算模型,建立了浮式风机气动—水动—气弹性耦合响应数值计算模型,如图3所示。气动力模块、水动力模块以及结构求解模块之间通过速度、位移、力和力矩信息的传递,实现了风力机气动载荷、平台运动响应、系泊张力以及叶片结构变形响应之间的耦合作用。需要说明的是,各计算模块的可靠性已经在之前的工作进行了验证[5,17],这里不再赘述。
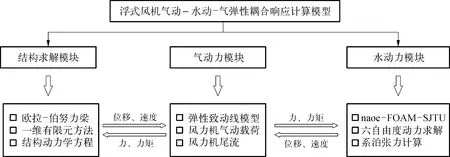
图3 浮式风机气动—水动—气弹性耦合计算模型
浮式风机气动—水动—气弹性耦合像响应的计算流程如图4所示。为了体现各模块之间的耦合作用,在平台运动响应的计算中,风力机的气动载荷和系泊张力会作为外载荷作用在平台上,而平台运动响应会反过来影响系泊点的位置以及风力机叶片的位置和相对风速,实现风力机—平台—系泊系统的耦合作用。此外,风力机的气动载荷作为外载荷会加剧叶片的结构变形响应,而叶片变形带来的位置和相对风速的变化也会影响到风力机的气动载荷,从而实现风力机气动响应和叶片结构变形之间的耦合,并最终实现浮式风机气动—水动—气弹性耦合响应模拟。
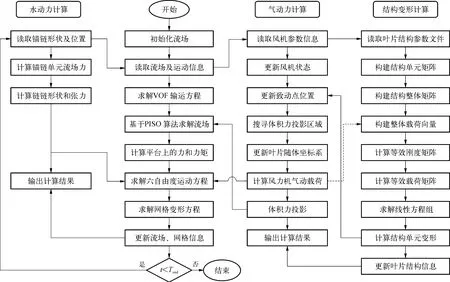
图4 浮式风机气动—水动—气弹性耦合响应计算流程
采用不可压缩N-S方程描述浮式风机耦合响应数值模拟中涉及的不可压两相流的非定常流动,流场的控制方程:
(12)
(13)
其中,U表示速度场;ρ代表两相流体的混合密度;Ug代表网格节点的速度;pd代表流场中的动压力;g代表重力加速度;μeff代表流体的有效动力黏度系数;fσ代表表面张力的源项,仅在气液交界面产生作用;fs代表消波源项,仅在消波区内起作用;fε代表由于风力机气动载荷投影到流场的体积力源项。此外,采用SST k-ω两方程模型对流体控制方程进行封闭求解。
2 计算设置
2.1 浮式风机模型
选用OC3(offshore code comparison collaboration,简称OC3)项目中的Spar型浮式风机作为研究对象[18]。该浮式风机由NREL 5-MW风力机和Hywind Spar平台组成,并采用悬链线式系泊系统,三根系泊缆绳均匀地分布在浮式支撑平台的周围。浮式风机的主要参数如表1所示[19-20]。
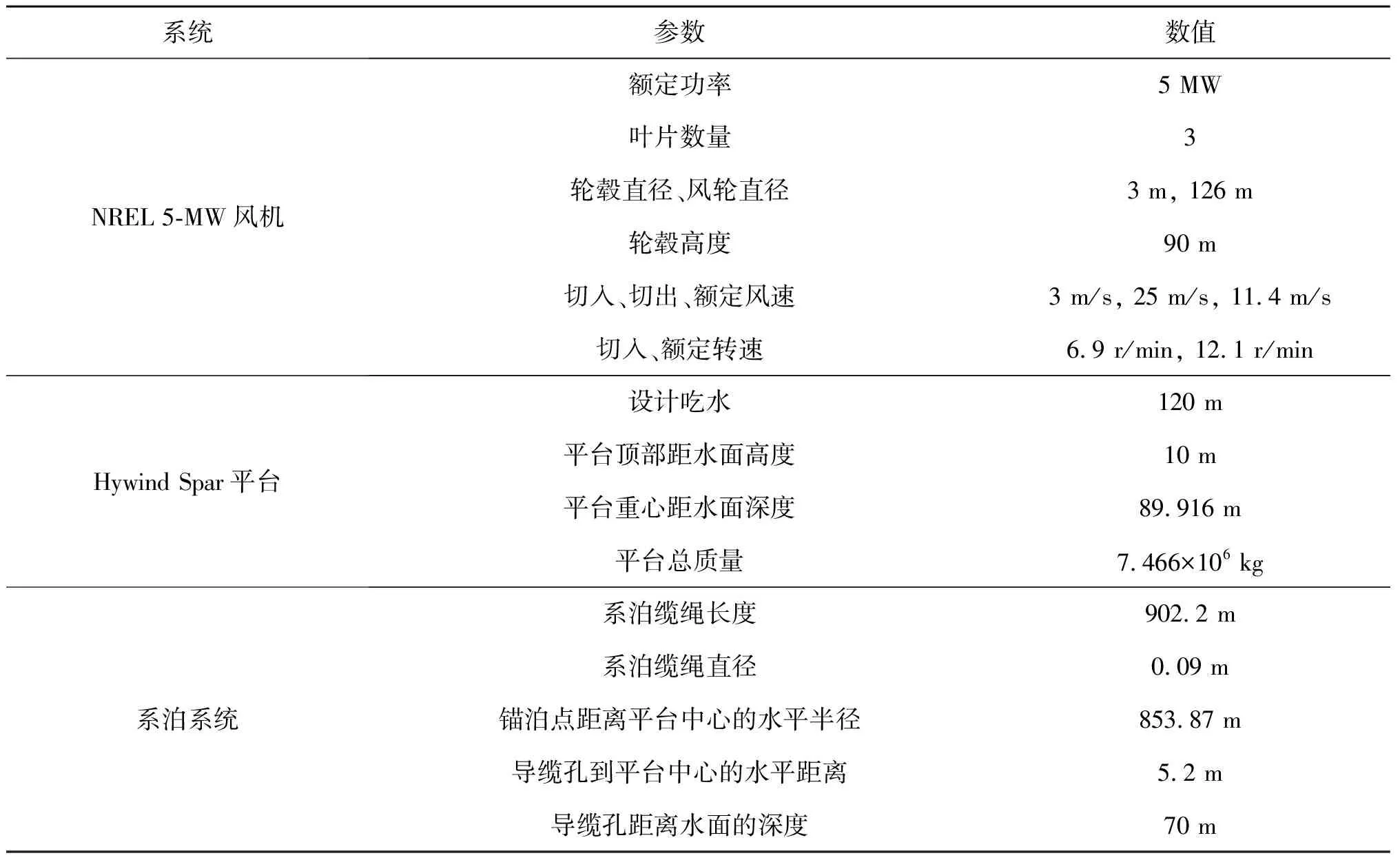
表1 OC3 Hywind Spar型浮式风机主要参数
2.2 计算域及网格布置
风浪联合作用下浮式风机耦合响应数值模拟采用的计算域如图5所示。计算域的长为784 m,宽为384 m,空气的高度设置为280 m,约为2.2D(D=126 m表示的风力机的直径)。为了减小计算量,水深设置为224 m,约为0.7d(d=320 m表示真实水深),此时水深对平台运动响应的影响可以忽略。风力机位于计算域的中间位置,距离入口边界约为1.1λ(λ=146.9 m表示入射波的波长),距离出口边界约为5D。为了避免波浪反射对平台运动产生影响,在出口边界前200 m的区域内设置消波区。
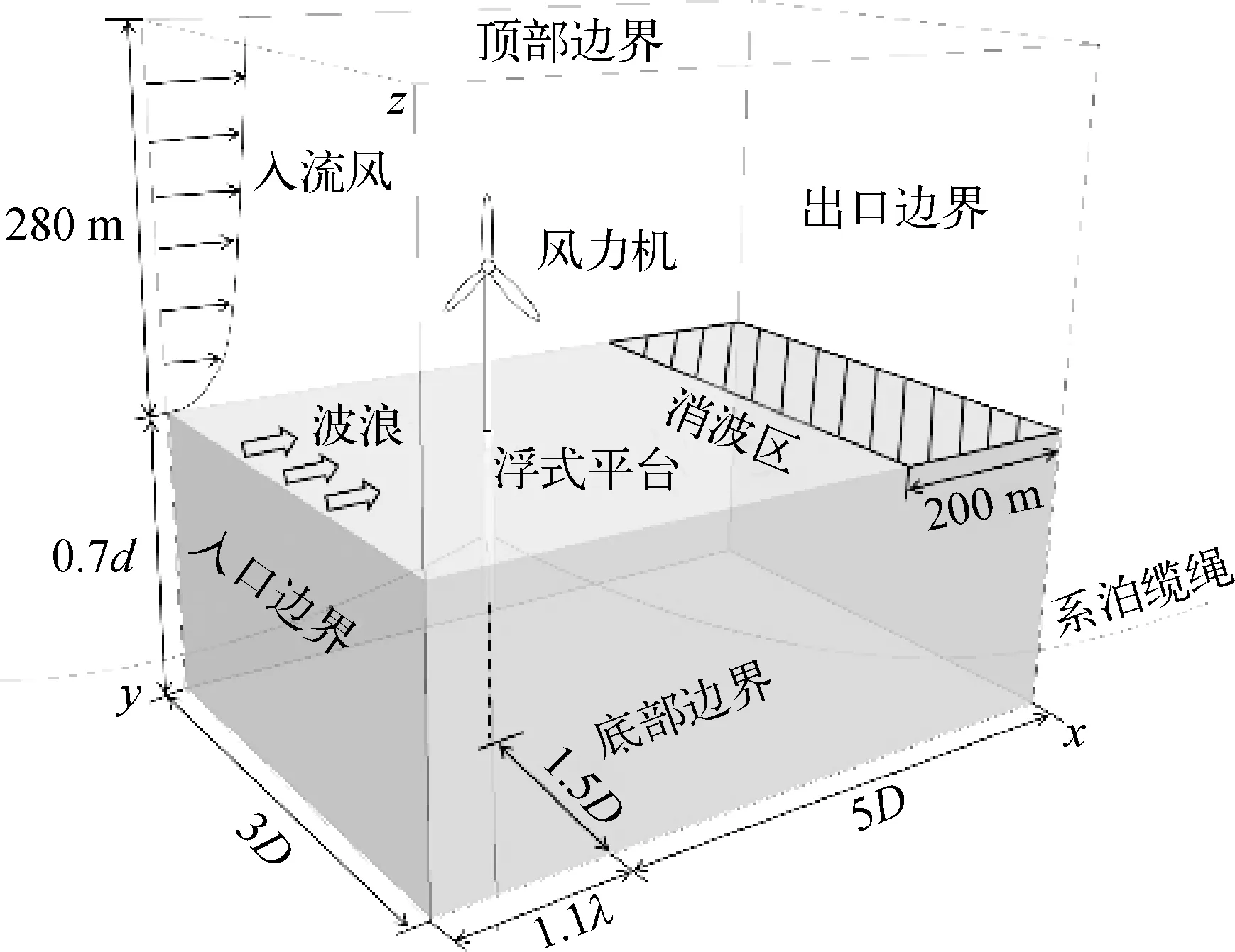
图5 计算域布置情况
计算域中的网格布置情况如图6所示,包括背景网格和加密网格。其中,背景网格沿x轴和y轴方向的尺寸均为8 m。为了减小计算域中的网格数量,背景网格的尺寸从自由液面处沿z轴正负方向线性增大,自由液面附近的背景网格尺寸为2 m,而计算域顶部和底部边界处的背景网格尺寸增大到20 m。进一步地,为了准确捕捉到浮式风机的尾流发展情况,并减小波浪的耗散,对风力机的尾流区以及自由液面附近的背景网格进行加密,加密后的背景网格尺寸为2 m×2 m×0.5 m(自由液面)和2 m×2 m×2 m(尾流区域)。同时,对平台附近的背景网格进行加密处理。计算域中的网格总量为559万。

图6 计算域中网格分布
2.3 风浪耦合入流条件
采用一阶Stokes规则波作为入射波,参考相关文献[18]中5级海况条件的设定,波高设置为3.66 m,波浪周期为9.7 s。此外,入流风速采用均匀入流形式,风速大小设置为11.4 m/s,对应的风轮转速为12.1 r/min。在数值模拟过工程中,不考虑风力机的转矩控制和变桨控制,因此风力机的转速始终保持不变,而叶片的桨距角始终设置为零。
计算域的入口边界采用Dirichlet边界条件,根据入流风速和波浪类型计算不同位置处的速度,压力梯度设置为零;计算域的出口边界和顶部边界均采用零压力梯度条件;计算域的底部边界采用滑移边界条件;计算域的左右两侧边界采用OpenFOAM中定义的对称边界条件,即垂直于边界的方向导数为零。
3 算例结果分析
3.1 网格收敛性验证
在开展浮式风机气动—水动—气弹性耦合响应数值模拟之前,首先对计算网格进行收敛性验证。采用三套不同密度的网格开展收敛性验证计算,具体网格信息如表2所示。计算风速同样设置为11.4 m/s,采用均匀入流条件,不考虑风力机的控制系统。同时为了减少计算稳定所需的时间,不放开浮式平台的自由度。计算采用的时间步长为0.01 s,小于文献[21]中对计算收敛所需的最小时间步,同时也满足CFL条件。

表2 网格收敛性测试中的网格参数信息
图7显示了不同网格密度条件下风力机的气动载荷系数随时间变化的情况。从图中可以看出,风力机的气动载荷在20 s后逐渐稳定下来。取30~50 s内的气动载荷数据进行统计分析,可以发现,采用中等网格计算得到的风力机气动载荷系数与采用精细网格的计算结果之间的误差仅为1.5%(Cp)和0.9%(Ct),而粗糙网格与精细网格之间的误差达到了8.8%(Cp)和4.5%(Ct)。进一步地,对采用不同网格密度计算得到的风力机叶尖处的结构变形响应进行统计,如表3所示。可以发现,中等网格和精细网格计算得到的叶尖处变形响应的误差在1%以内。综上,为了平衡计算效率和计算时间,下面将采用中等密度网格开展浮式风机耦合响应数值模拟。
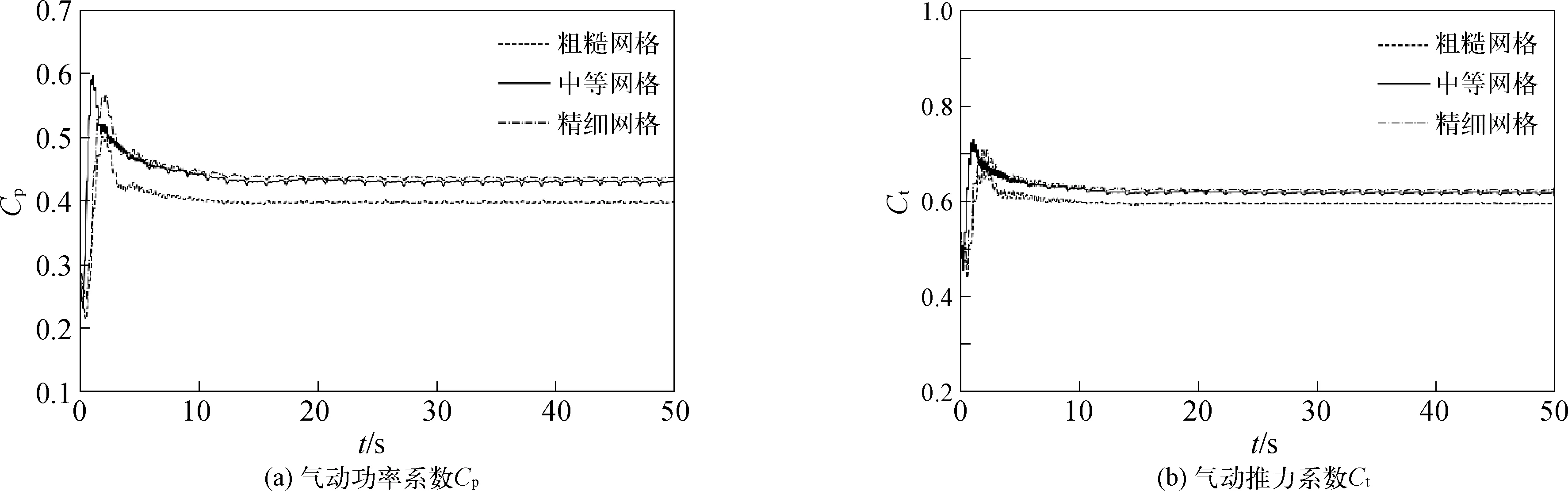
图7 网格收敛性测试中气动载荷系数的时历曲线

表3 网格收敛性测试中风力机叶尖结构变形响应
3.2 叶片结构变形响应
浮式风机在正常运行过程中,其叶片会在重力、离心力以及气动载荷的作用下产生明显变形,并会进一步对浮式风机的耦合性能产生影响。图8显示了浮式风机的叶片(Blade #1)在不同方向上的结构变形响应,包括不同时刻瞬时变形情况以及结构变形响应的时空分布云图。
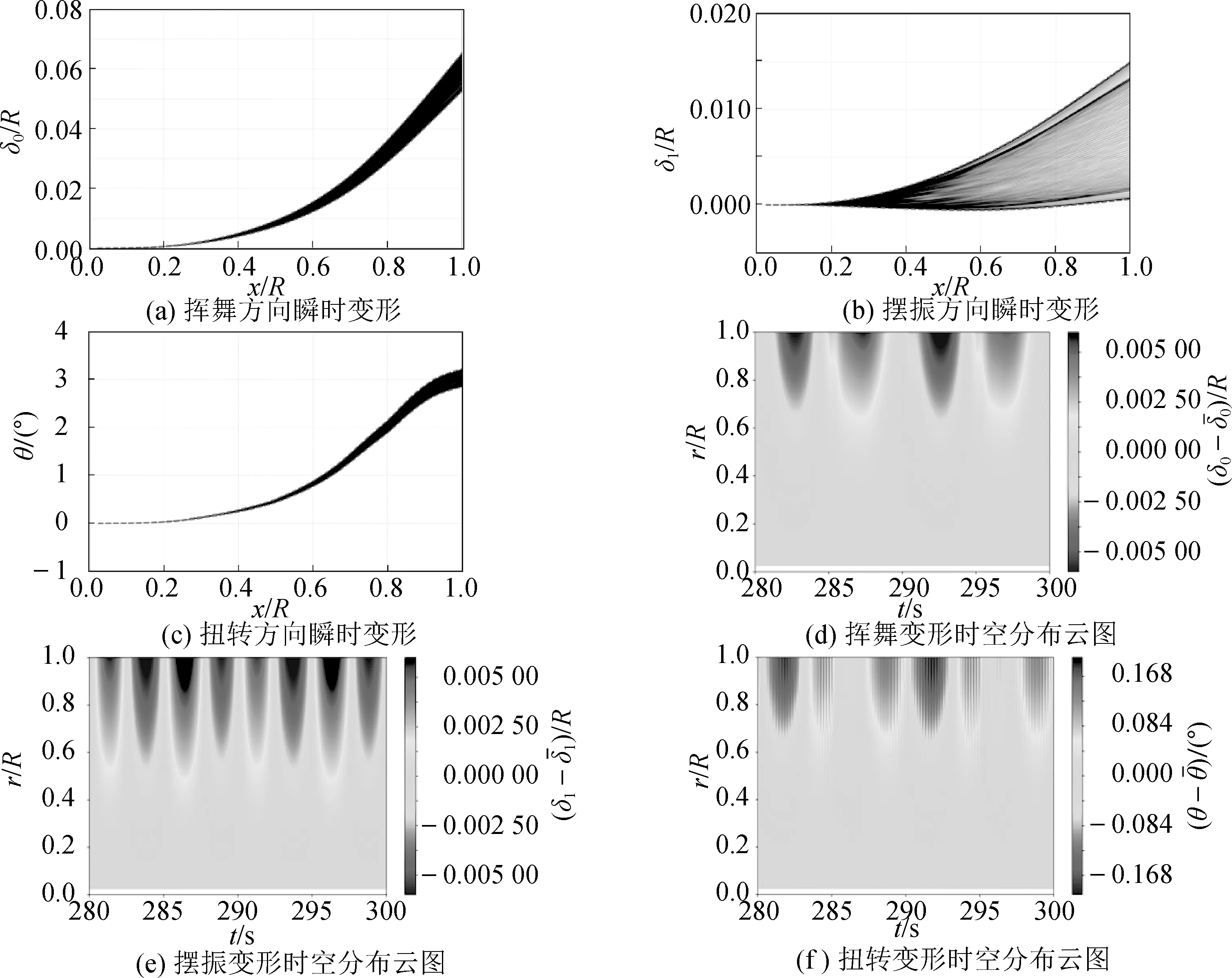
图8 风力机叶片(Blade #1)结构变形响应
对于叶片结构瞬时变形图,黑色实线表示叶片在某一时刻的结构变形位移,虚线代表叶片瞬时变形的包络线;对于叶片结构变形时空分布云图,横坐标表示时间,纵坐标表示叶片截面沿径向的相对位置,并采用叶片瞬时变形幅值对云图进行染色。从图中可以看出,浮式风机的叶片在不同方向均产生了明显结构变形。在叶片挥舞方向上,由于气动推力的作用,叶片弯曲变形的平均值较大,由于是均匀入流条件,气动推力的变化幅值不大,因此叶片挥舞变形的波动幅值相对较小。沿叶片摆振方向,叶片受到周期性变化的重力的影响,其摆振变形的波动幅值较大。相较于挥舞变形,由于叶片摆振方向的抗弯刚度更大,且受到的气动载荷较小,因此叶片摆振变形的平均值明显小于挥舞变形。此外,叶片沿轴向的扭转变形主要受到气动扭矩的影响,与气动推力类似,叶片受到的气动扭矩在均匀入流条件下的波动幅值较小,因此叶片扭转变形的波动程度较低。值得注意的是,叶片扭转变形会直接影响到叶片的局部攻角,进而会明显改变风力机的气动性能。
从叶片结构变形响应的时空分布云图可以看出,叶片的结构变形响应呈现出明显的周期性变化特征。其中,叶片挥舞变形的变化周期与波浪周期相近,约为9.7 s,这主要是受到周期性波动的气动推力的影响。而叶片摆振变形的波动周期接近5 s,与风轮旋转周期相近,这表明引起叶片摆振变形周期性波动的主要因素是叶片自身重力。从叶片扭转变形的时空分布可以看出,其变化周期同时包含波浪周期和风轮旋转周期的特性。进一步地,取浮式风机计算稳定后200~300 s内的数据进行统计分析,计算叶尖位置结构变形响应的均方根(RMS)和标准差(STD),如表4所示。RMS主要反映叶片结构变形响应的有效值,而STD主要反映叶片结构变形响应的波动程度。叶片挥舞变形的RMS可达3.09 m,显著大于叶片沿摆振方向的弯曲变形。但叶片摆振变形的STD略大于叶片挥舞变形的STD,说明摆振变形的波动程度更加显著。此外,叶片扭转变形的RMS为3.07°,这会显著改变叶片的局部攻角,进而影响风力机的气动载荷。周期性变化的结构变形响应会对叶片的疲劳寿命产生明显损伤。

表4 叶尖位置结构变形响应的均方根和标准差
3.3 风力机气动载荷响应
由于叶片结构变形响应与风力机气动载荷之间的耦合作用,叶片变形会对浮式风机气动载荷产生影响。为此,分别对浮式风机在考虑和不考虑叶片变形两种情况下的耦合响应进行了数值模拟,并对比了两种不同情况下风力机的气动载荷系数,如图9所示。
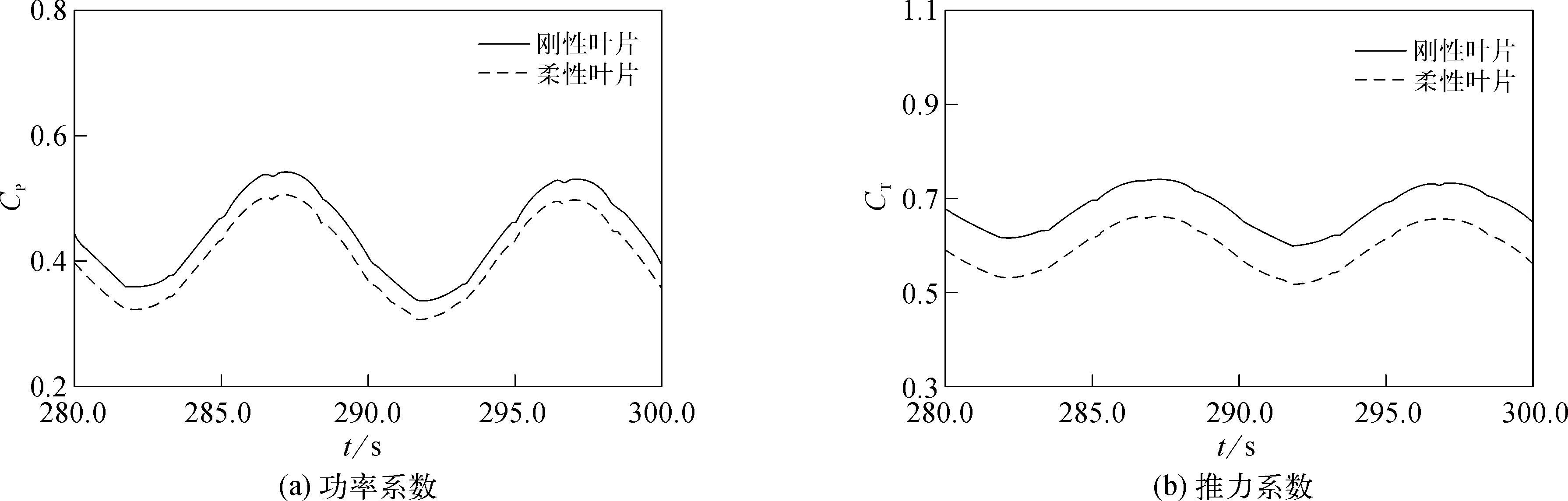
图9 浮式风机气动载荷系数的时历曲线
图例中“刚性叶片”表示不考虑叶片变形时的情况,“弹性叶片”表示考虑叶片变形时的情况。无论是否考虑叶片结构变形响应,浮式风机的气动载荷系数均呈现出明显的周期性变化的特征,变化周期接近波浪周期,这主要是由于平台运动引起的入流风速周期性变化导致的。在考虑叶片变形时,浮式风机的气动载荷系数明显减小。其中,气动功率系数CP的RMS降低了约7.8%,而气动推力系数CT的降幅更大,达到了11.8%。此外,CP的STD降低了约2.8%,CT的STD增大了约4.2%。这表明,叶片结构变形会导致浮式风机气动载荷平均值和波动幅值的降低。相较于气动功率,气动推力受到叶片结构变形的响应更加显著,同时,气动载荷平均值比其波动幅值受叶片变形的影响更大。
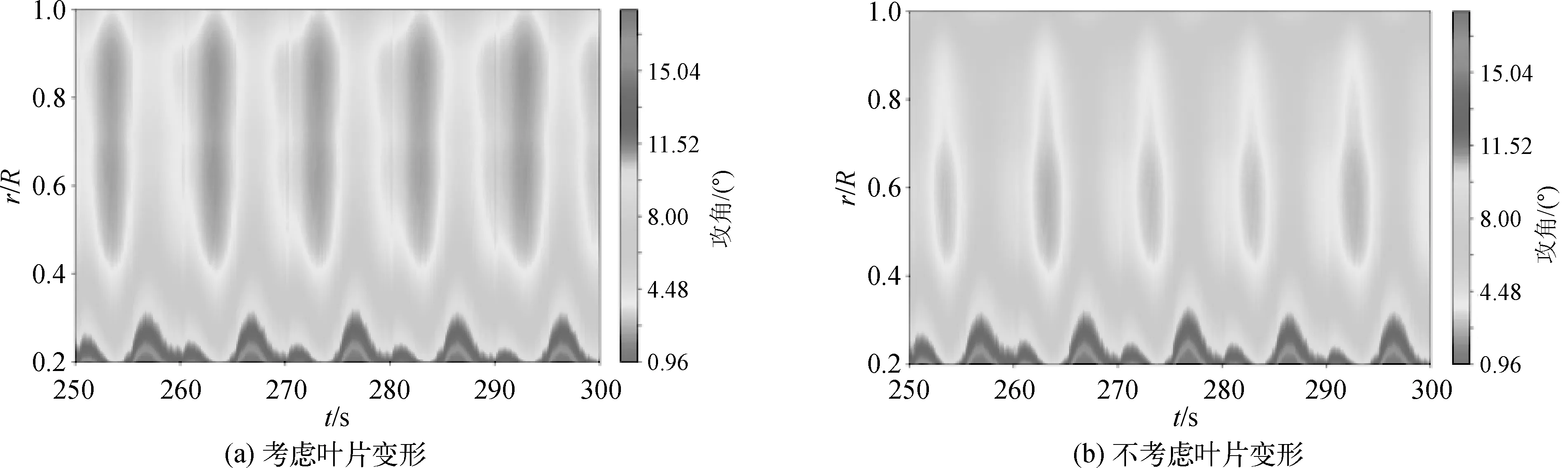
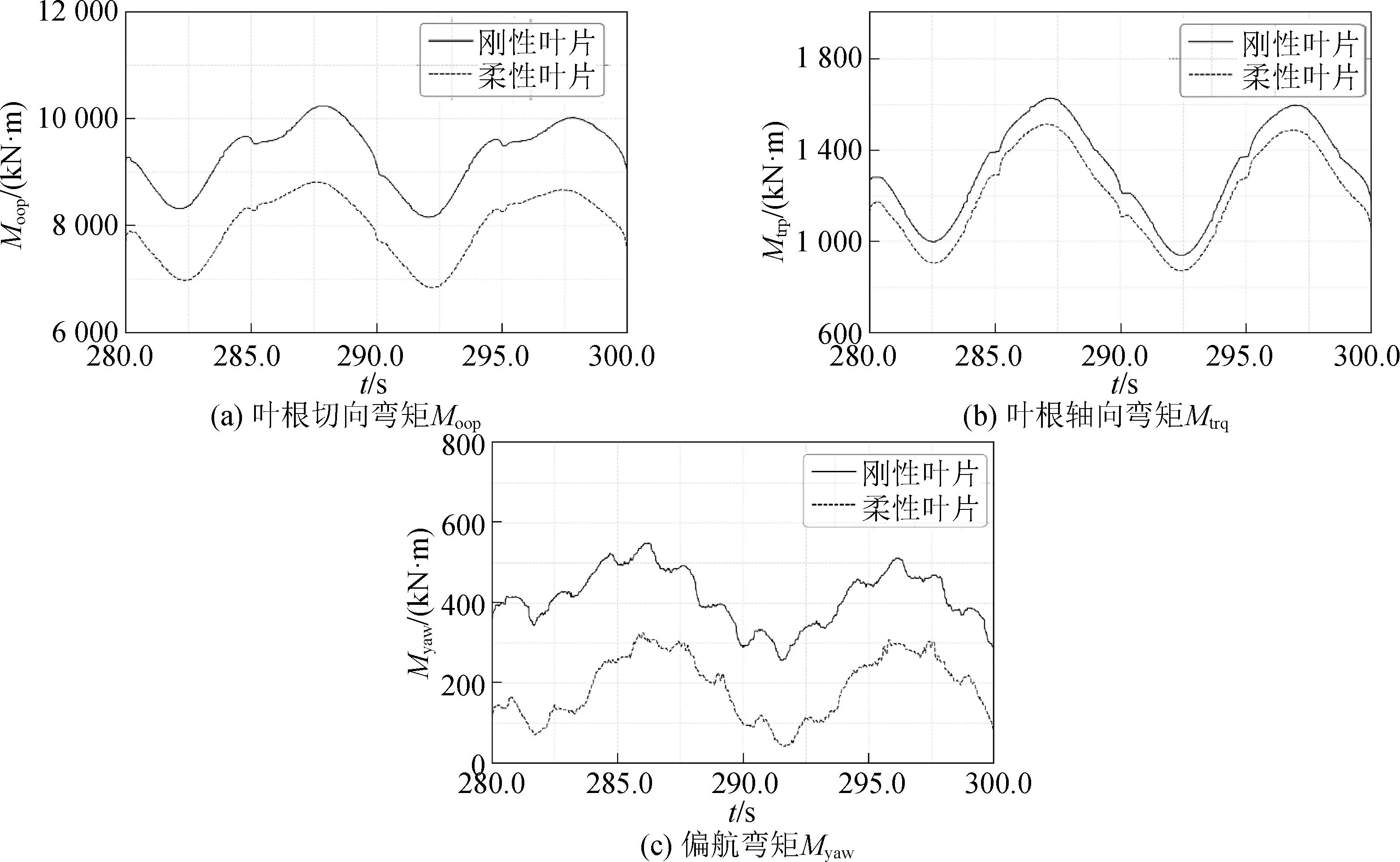
叶片结构变形对浮式风机气动载荷的影响主要包括以下两个方面:一方面,叶片弯曲变形会使得风轮迎风面积减小,从而降低了风力机受到的气动推力,导致气动推力的RMS降低;另一方面,叶片结构变形显著改变了风力机的入流条件,从而对浮式风机的气动载荷产生影响。由风力机气动载荷的计算方式可知,轴向入流风速和叶片局部攻角是影响风力机气动载荷的关键因素。图10和图11分别对比了浮式风机的叶片(Blade #1)在是否考虑叶片变形情况下轴向入流风速Ua和局部攻角α。可以发现,在考虑叶片变形时,相对位置(x/R)在0.5~0.9范围内的局部叶片的入流风速有一定程度的增大,这有利于提高风力机的气动载荷,由于扭转变形的影响,该范围内叶片的局部攻角反而明显减小,尤其在叶尖区域附近(0.7 图10 浮式风机叶片(Blade #1)轴向入流风速(Ua)时空分布云图 图11 浮式风机叶片(Blade #1)攻角时空分布云图 进一步地,叶片变形引起的气动载荷变化会对浮式风机的叶根弯矩和偏航力矩产生影响。图12对比了不同叶片变形情况下叶根切向弯矩Moop、叶根轴向弯矩Mtrq以及偏航力矩Myaw的时历曲线。与气动载荷的变化类似,在考虑叶片变形时,Moop、Mtrq和Myaw的RMS都有所减小,其中,Myaw的降幅最大,达到了49.8%,Mtrq的降幅最小,为7.8%,Moop的降幅为14.3%。考虑到Moop和Mtrq分别由气动推力和气动升力积分得到,进一步表明叶片变形对气动推力的影响更加显著。此外,叶片结构变形对叶根弯矩及偏航力矩的波动幅度的影响不大。 图12 风力机叶片(Blade #1)叶根弯矩及偏航力矩的时历曲线 由于风力机和浮式平台之间的耦合作用,风力机的气动载荷会对浮式平台及系泊系统的水动力响应产生影响。表5对作用在浮式平台上的气动力载荷和水动力载荷进行了总结。可以发现,气动力载荷沿x方向的水平分量远大于水动力载荷,这会显著增大浮式平台的纵荡位移。此外,气动力在载荷绕y轴的纵摇力矩也明显大于水动力载荷在相应方向上的分量,这会增加浮式平台的纵摇角。但气动力载荷作用在平台上的纵摇力矩的波高幅值远小于水动力载荷,因此其对平台纵摇运动的幅值影响较小。此外,气动力载荷沿z轴方向的水平力和绕z轴的力矩会增大浮式平台的垂荡和艏摇运动幅值。进一步地,对不同叶片变形情况下浮式平台的六自由度运动响应进行分析,如图13所示。在考虑叶片结构变形时,浮式平台纵荡、纵摇运动响应的平均值有所减小,但波动程度变化不大。其中,浮式平台纵荡位移的平均值降低了约12.1%,平台纵摇角的平均值下降了约11.9%,这主要是浮式风机在叶片变形时气动推力的降低导致的。此外,叶片变形使得浮式风机的偏航力矩有所减小,从而导致浮式平台的艏摇运动响应的平均值和波动幅值均有所下降,但变化幅值不大。此外,由于气动载荷在沿y轴和z轴方向的分量较小,因此叶片结构变形引起的气动载荷变化对浮式平台的横荡、横摇和垂荡运动的影响较小。 表5 浮式平台受到的气动力载荷与水动力载荷统计表 平台运动响应的变化会进一步引起系泊缆绳张力的改变。图14显示了不同的叶片变形下系泊缆绳的张力随时间的变化情况。由于#2和#3系泊缆绳沿x轴方向成对称布置,其系泊张力的大小及变化趋势几乎一致,因此仅对#1和#2系泊缆绳的张力进行对比分析。对比平台纵荡运动的时历曲线,可以发现,#2系泊缆绳张力的变化趋势与平台纵荡位移的变化趋势一致,而#1系泊缆绳张力的变化趋势与之正好相反。系泊缆绳的张力变化主要受到平台纵荡位移的影响,在考虑叶片变形时,平台纵荡位移的平均值有所减小,相应的#1和#2系泊缆绳的波动幅值分别下降了约4.1%和2.3%。 图14 系泊缆绳张力的时历曲线 图15 轮毂高度平面内时均尾流速度云图 图16 轮毂高度平面内涡量场云图 进一步地,图17对比了不同叶片变形状态下轮毂高度平面内的湍动能分布云图。在叶片所在位置,由于风速的剧烈变化,此处的湍动能较大。在风轮后方,湍动能最初主要分布在尾流区与周围环境之间的剪切层内。随着尾流距离的增加,尾涡逐渐翻卷失稳,流动不稳定性增加,尾流中的湍动能随之增大,湍动能的分布范围也逐渐从剪切层向尾流中心区域发展。对比不同叶片变形情况下的湍动能分布,在考虑叶片变形时,尾流中湍动能明显增大的位置从x/D=3附近后移到x/D=4附近,这与尾涡翻卷失稳位置的变化是一致的,表明尾涡翻卷失稳是引起尾流中湍动能增强的主要因素之一。此外,在叶片变形情况下,尾流场中的湍动能明显小于不考虑叶片变形时尾流中的湍动能,表明叶片变形会使得风轮后方尾流中的湍动能有所减小。 图17 轮毂高度平面内湍动能分布云图 基于两相流CFD求解器naoe-FOAM-SJTU,结合弹性致动线模型和等效梁理论,建立了浮式风机气动—水动—气弹性耦合响应计算模型,并对均匀风和规则波作用下浮式风机的耦合响应特性开展了数值模拟,探究了叶片结构变形响应、风力机气动载荷、浮式平台运动响应以及系泊张力之间的耦合作用,对并浮式风机的复杂尾流场特性进行了分析。结果表明,在气动载荷和自身重力的作用下,风力机叶片会产生显著的结构变形,叶片挥舞变形的平均值大于叶片摆振变形,而叶片挥舞变形波动幅值则小于叶片摆振变形。受气动载荷的影响,叶片挥舞变形呈现出周期性变化特性,变化周期与波浪周期相近,而叶片摆振变形主要受到自身重力的影响,其变化周期与风轮旋转周期相近。叶片扭转变化会显著降低浮式风机的气动载荷,包括气动功率、气动推力、叶根弯矩以及偏航力矩。相较于气动功率,气动推力受叶片变形的影响更加显著。由于平台运动响应的影响,风力机气动载荷呈现出大幅度周期性波动的特征,波动周期与波浪周期相近,而在气动载荷的影响下,浮式平台的纵荡位移和纵摇角会显著增加,垂荡和艏摇运动幅值也随之增大。此外,叶片变形引起的风力机气动载荷的下降,会导致浮式支撑平台纵荡、纵摇以及艏摇运动响应平均值的减小,而系泊张力的波动幅值也随着平台纵荡位移的减小而有所下降。进一步地,叶片变形使得浮式风机在轮毂高度平面内的尾流速度损失有所减小,并导致尾流场中尾涡失稳的位置向后移动,同时会使得尾流中的湍动能水平有所降低。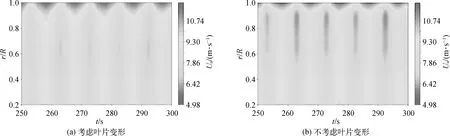
3.4 浮式平台水动力响应
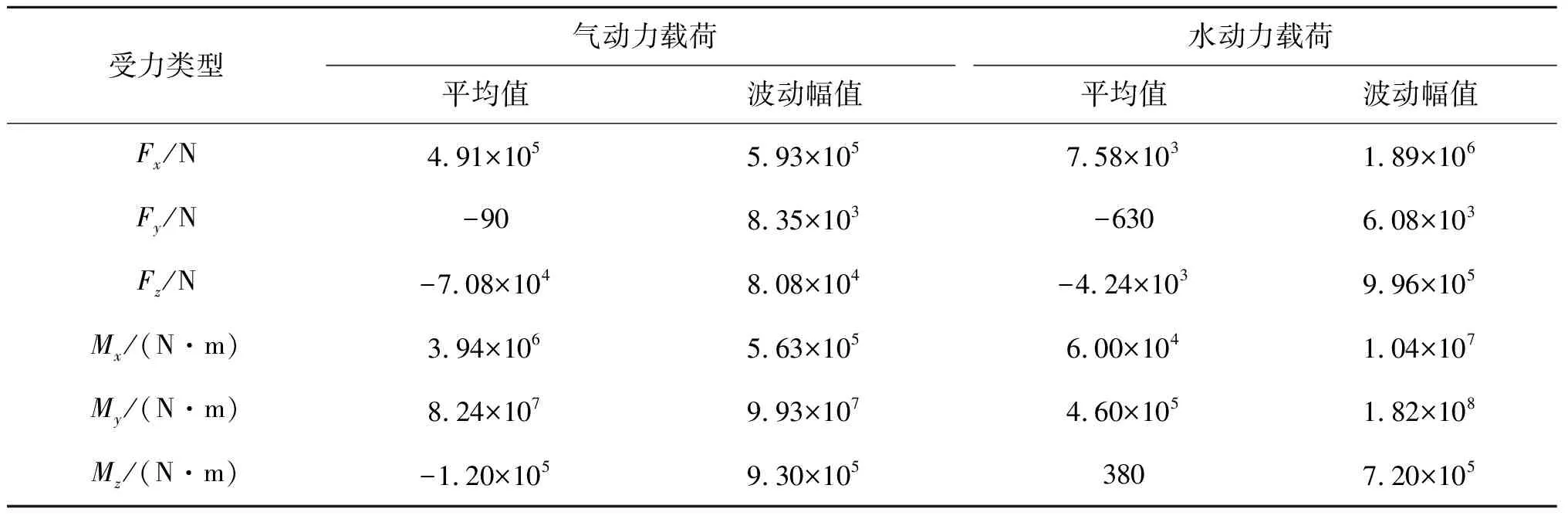
3.5 浮式风机尾流场特性
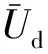



4 结 语
