小型自然循环铅铋快堆无保护超功率事故不确定性分析研究

余清远 漆静雯 赵鹏程 赵亚楠 于 涛

（南华大学核科学技术学院 衡阳421001）

采用液态铅铋冷却的铅铋堆在嬗变核废料和增殖核燃料方面具有独特优势，拥有良好的经济性和固有安全性，被第四代国际核能论坛预计有望成为首个实现工业示范化的第四代核能系统［1］。事故瞬态是铅铋快堆热工安全分析的重要内容，有必要探究铅铋堆瞬态过程中关键参数的变化规律，评估铅铋堆的固有安全性。由于设计参数、初始边界条件等因素的影响，铅铋堆瞬态模拟计算结果不可避免地存在不确定性，将不确定性分析方法应用铅铋堆瞬态事故分析，可量化不确定性分析结果，评估瞬态工况中输入参数对铅铋堆安全的影响，对铅铋堆的设计分析、安全审评具有现实意义。

国际上，国际性合作研究项目OECD（Organization for Economic Co-operation and Development）/NEA LWR UAM（Nuclear Energy Agency，Light Water Reactor，Uncertainty Analysis in Modeling）正在全力开展有关多物理场、多尺度耦合的不确定性分析［2-5］；日本基于京都大学临界装置开展了一系列加速器驱动系统实验，并采用随机采样技术对实验开展了不确定性量化分析［6-9］；瑞典皇家理工学院基于ROAAM+、MELCOR 等程序对北欧沸水堆开展了不确定性量化和敏感性分析［10-13］；由美国阿贡实验室牵头的先进反应堆E级高性能模拟中心开展了堆芯物理计算的不确定量化分析和敏感性分析［14-15］。近年来，国内有关快堆的不确定性研究主要集中于不确定性分析方法：西安交通大学先后采用不确定性分析方法开展了钠冷快堆事故SHRT-17 试验数据和BN-600 快堆有效增值因数的不确定性和敏感性分析［16-17］；哈尔滨工程大学基于抽样统计法开展了中国实验快堆（China Experimental Fast Reactor，CEFR）的不确定性分析和敏感性分析［18］；中国原子能研究院采用多种不确定性分析方法开展了CEFR堆芯设计计算的不确定度定量评价［19］。中国科学技术大学针对铅铋快堆开发了多物理多尺度程序Fluent/KMC-sub/NDK［20］，并对SNCLFR-100开展了启堆条件下的流动不稳定性分析［21］。而铅铋快堆作为具有发展潜力的候选堆型之一，其瞬态安全特性对反应堆运行至关重要，开展铅铋快堆的瞬态事故的不确定性量化分析，研究瞬态事故的不确定性来源，对铅铋快堆的设计、安全特性评估有重要意义。

本工作是针对中国科学技术大学和南华大学联合设计的小型自然循环铅基铅铋快堆（Small Natural Circulation Lead-bismuth Cooled Fast Reactor 10 MWth，SNCLFR-10），首先，通过文献资料以及工程经验判断，考虑三类不确定性输入参数：热工水力模型参数、中子物理模型参数以及燃料制造公差；然后，基于课题组自主开发的物理/热工耦合不确定性量化分析程序CFD/PFS 程序开展无保护超功率事故的不确定性分析，采用拉丁超立方（Latin Hypercube Sampling，LHS）对输入参数进行抽样，对瞬态安全参数进行不确定性量化分析，并通过相关系数分析法评估输入参数对瞬态安全参数的敏感度。

1 计算模型

1.1 分析模型

SNCLFR-10 堆是由中国科学技术大学和南华大学联合设计的小型自然循环铅铋快堆，具有良好的现实可行性、安全可靠性、实验灵活性和技术延续性［22］。图1 为SNCLFR-10 堆的结构设计图，表1、2给出了反应堆设计参数及堆芯主要设计参数。SNCLFR-10堆的热功率为10 MW，燃料采用富集度为19.75%的UO2，燃料包壳材料采用316Ti不锈钢。堆芯活性区由94盒组件组成，其中86盒燃料组件，8盒控制棒组件。一回路冷却剂系统采用自然循环驱动液态铅铋冷却，冷却剂入口温度为533.15 K，出口温度为663.15 K；二回路冷却剂采用4 MPa 的加压液态水。

表1 SNCLFR-10主要设计参数Table 1 Main design parameters of SNCLFR-10

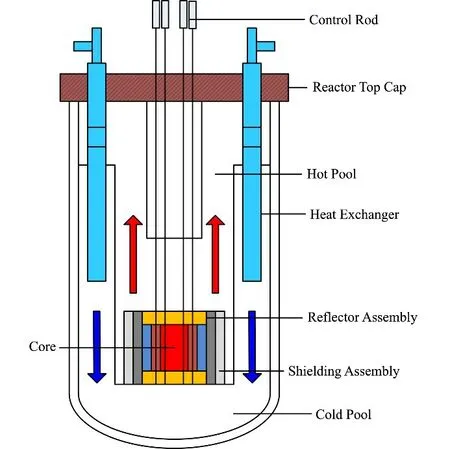
图1 SNCLFR-10堆结构示意图Fig.1 Structure diagram of SNCLFR-10

无保护超功率事故（Unprotected Transient Overpower，UTOP）是指向反应堆内突然引入一个正反应性，导致功率急剧升高的瞬态过程，此过程中反应堆停堆保护系统失效。UTOP 事故的瞬态条件：反应堆初始工况为稳态运行，假设最大价值控制棒失去控制而不可抽出，故在2 s 内迅速引入1$正反应性，整个过程无停堆保护动作。

1.2 CFD/PFS程序

CFD/PFS 是基于CFD 程序FLUENT 的用户自定义函数（User Defined Function，UDF）耦合点堆中子动力学模型（Point Kinetics Model，PKM）、燃料棒热传导模型（Fuel Pin Heat Transfer Model，FPH）以及不确定性分析程序SIMLAB开发的一套物理热工耦合不确定性分析程序，可用于分析小型铅铋快堆的瞬态事故。SIMLAB 是研究不确定性的开源程序，由欧洲联合研究中心主持研究开发，配备可视化操作界面，其中含有统计预处理子系统、模型执行子系统、统计后处理子系统，广泛用于不确定性和整体敏感性研究［23］。采用与SIMMER 程序code-to-code的方法进行CFD/PFS 的对比验证，CFD/PFS 程序开发与详细验证见参考文献［24］。

CFD/PFS程序分为物理热工耦合计算模型与不确定性分析计算，其计算流程如图2 所示。物理热工耦合计算模型包括CFD模型、点堆中子动力学模型、燃料棒热传导模型。PKM是三维时空动力学的简化模型，采用6 组缓发中子的点堆动力学方程主要用于计算反应性变化：

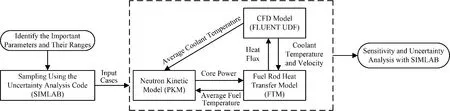
图2 CFD/PFS数据传递流程Fig.2 The data transfer route of CFD/PFS

式中：n（t）是中子密度；ρ（t）是反应性；β是缓发中子总份额；βi是i组缓发中子的份额；Λ是中子代时间；λi是第i组缓发中子的衰变常数；Ci是i组缓发中子先驱核的浓度。

再根据反应性通过点堆动力学方程求解相对中子密度n（t），则总功率为：

反应性反馈源于反应堆温度、压力或者流量的变化，而温度对反应性的影响是主要反馈，故所有反应性反馈、堆内温度总反应性公式可表示为：

式中：KD为多普勒系数；αc，a为堆芯轴向膨胀反馈系数；αc，γ为堆芯径向膨胀反馈系数；αc为冷却剂温度反馈系数；Tf（t）和Tf（0）分别为t时刻的燃料、冷却剂平均温度。

FTM包括燃料棒稳态和瞬态热传导模型，主要用于计算燃料棒的温度分布，包括燃料芯块、气隙以及包壳的温度，提供热流密度给CFD 模型，反馈芯块平均温度给PKM；CFD模型主要用于计算堆芯热工水力参数，包括冷却剂的温度、速度等，反馈冷却剂平均温度给PKM，提供冷却剂温度和速度给FTM。不确定性分析计算流程如下：1）确定重要输入参数及其分布范围；2）利用SimLab程序对不确定性输入参数抽样，生成输入工况；3）将输入工况传递给物理热工耦合计算模型进行计算，生成输出工况；4）将输出工况传递给SimLab程序，对结果进行不确 定性分析和敏感性分析。

表2 SNCLFR-10堆芯主要设计参数Table 2 Core design parameters of SNCLFR-10

2 不确定性方法及关键参数识别

2.1 不确定性分析方法

本工作基于拉丁超立方抽样的非参数统计法进行不确定性分析，拉丁超立方采取分层抽样，LHS抽样过程如下：1）根据输入参数的数量及分布范围等概率的分成n个区域；2）在每个区域内进行随机抽样；3）将抽样产生的样本进行随机组合；4）挑选满足约束条件的组合样本作为输入参数样本。与随机抽样的蒙特卡罗方法比较，拉丁超立方抽样可用较少样本完成不确定性量化，且在均值和方差的估计上有显著改善。

非参数统计法（wilks 公式）根据分布区间的置信度β以及输出参数的概率γ确定所需最小抽样数目n。wilks公式如下：

其中，式（4）适用于单侧限值分布，式（5）适用于双侧限值分布。

由wilks 公式计算出的满足不同置信度和容许区间的最小样本量n值如表3 所示。根据非参数统计理论，最小样本量选取59 时，目标参数的容忍上限值取最大值；最小样本量选取93 时，目标参数的容忍上限值取次大值［25］。

表3 不同置信度和容许区间下最小样本信息分布Table 3 The minimum number of samples under different confidence and tolerance intervals

2.2 关键参数的选取

反应堆瞬态计算中的不确定性输入参数主要考虑三部分：1）物理模型输入参数；2）热工水力模型输入参数；3）燃料制造公差输入参数。针对SNCLFR-10堆的UTOP事故，根据始发事件选取清单、文献资料以及工程经验判断等方式选取不确定性输入参数，并确定其范围和概率密度分布。选取的不确定输入参数分为三个部分：首先是几何输入参数，一些参数测量有一定的不安全性故缺乏，只能由专家假设估算；其次是中子学参数，因为实验测量系统及统计误差，故其引入的不确定性需考虑；最后是热工水力参数，程序、模型及经验关系式等都会引入不确定性，故选取其中最典型5 个参数。表4 列出了25 个不确定输入参数信息，输入参数服从均匀分布或正态分布，其中不确定性度表示参数名义值（设计值）和参数上下限值的相对偏差。

表4 不确定性输入参数信息Table 4 Uncertainty distribution of input parameter

由于测量仪器精准、技术先进，反应堆部件制造精度高，因此燃料制造公差输入参数的不确定度设为±0.5%。中子代时间、缓发中子份额、衰变常数以及初始功率的不确定度参考其他类似反应堆的不确定度；对于反应性反馈系数，考虑它包含了一系列不确定性（材料属性、几何形状、截面数据以及蒙特卡罗计算），为保证其保守性，将反应性反馈系数的不确定度设为10%［26］。热工水力现象极其复杂，热工物性参数大多是根据实验数据拟合以及经验关系式所得，因此热工水力模型输入参数通常存在较大的不确定度［27］。

2.3 关键参数的抽样

基于SIMLAB程序采用拉丁超立方方法实现不确定性输入参数抽样，种子数设定为98 765。根据wilks 非参数统计法，在95%置信水平、95%概率水平下，所需最小计算次数为93次。考虑到抽样可能存在坏点、程序可能运行失效等原因，抽样数目设定为100 组，其中每一组工况包括25 个输入参数。为直观地观测输入参数的概率分布特征、检测其抽样的合理性，对不确定性输入参数进行归一化处理。图3为不确定性输入参数的拉丁超立方抽样样本归一化结果。

图3 不确定性输入参数抽样归一化结果Fig.3 Normalized result of input uncertainty parameter sampling

当输入参数分布类型为正态分布，抽样样本在分布范围内呈现为中间密集，两边稀疏；当输入参数分布类型为均匀分布，抽样样本在分布范围内呈均匀态势。由图3对比表4发现，选定各输入参数的概率分布类型准确无误。

3 不确定性与敏感性分析

3.1 不确定性量化分析

针对SNCLFR-10 堆的UTOP 事故不确定性分析，通过不确定性输入参数的组合量化反应性、堆芯功率、燃料中心温度以及包壳温度的不确定性。图6~9 为不同目标参数的变化情况，目标参数的名义值均处于95/95不确定包络带内，不确定性分析结果具有合理性，且不确定度上限没有出现过于保守的情况；对比不同目标参数的不确定性包络带，可知不同时刻输入参数的不确定性传播到目标参数的不确定性不同。

图4、5 为100 组工况下反应性与功率的变化情况，发生UTOP事故的2 s内，总反应性、总功率急剧增强。此阶段不确定带较小，随后由于燃料和冷却剂温度上升，负反应性反馈增强，且反应性反馈系数不确定度较大，促使反应性、功率的不确定带相对变宽，随着负反应性反馈作用，反应性与功率逐渐进入一个新的稳态。图6、7为100组工况下包壳温度、燃料温度的变化情况，UTOP事故发生后，随着功率的增大，燃料与包壳的温度迅速上升，之后由于负反馈效应增强，且反应性反馈系数不确定度较大，燃料与包壳温度的不确定带愈加明显，随着功率下降，燃料 与包壳温度逐渐进入稳态。

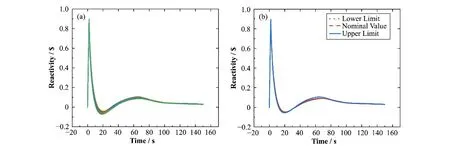
图4 反应性变化情况（100组工况）(a)与不确定性包络带(b)Fig.4 Changes of reactivity(100 sets of outputs)(a)and uncertainty bands(b)

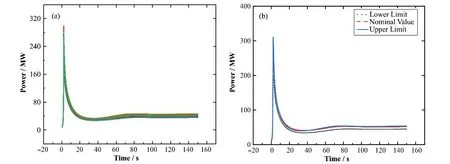
图5 功率变化情况（100组工况）(a)与不确定性包络带(b)Fig.5 Changes of power(100 sets of outputs)(a)and uncertainty bands(b)

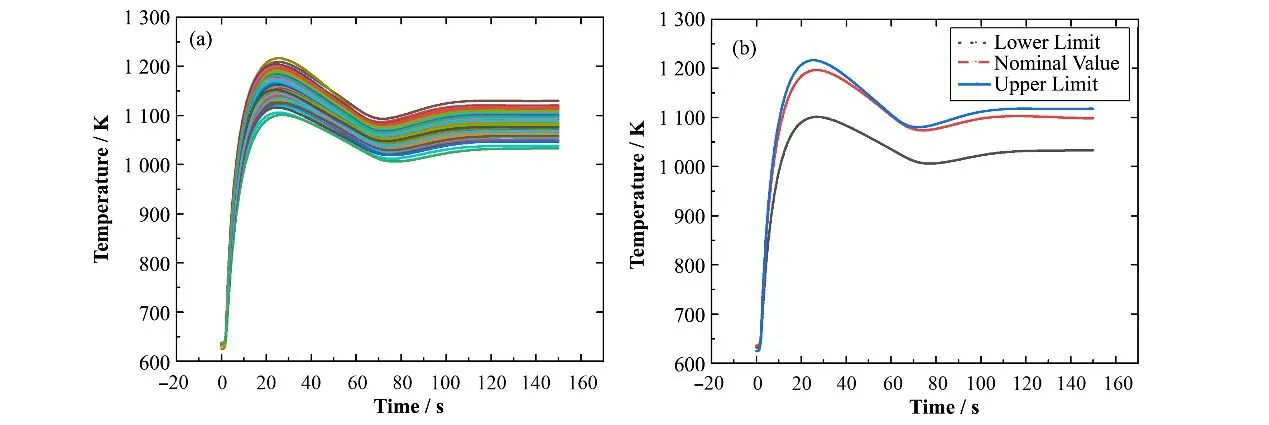
图6 包壳温度变化情况（100组工况）(a)与不确定性包络带(b)Fig.6 Changes of cladding temperature(100 sets of outputs)(a)and uncertainty bands(b)

图7 燃料温度变化情况（100组工况）(a)与不确定性包络带(b)Fig.7 Changes of fuel temperature(100 sets of outputs)(a)and uncertainty bands(b)

基于非参数统计理论，在SNCLFR-10 堆的UTOP 事故中取100 组工况的次大值作为目标参数容忍上限值。计算可得，包壳峰值温度的95/95容忍上限值为1 208.66 K，燃料峰值温度的95/95 容忍上限值为2 757.25 K。

3.2 敏感性分析

针对SNCLFR-10 堆UTOP 事故的敏感性分析，本工作基于SIMLAB 程序采用Spearman 秩相关分析方法研究输入参数对燃料最高温度以及包壳最高温度的敏感度。Spearman 秩相关分析法用于全局敏感性分析，可分析多个输入参数对目标参数的影响。相关系数取值范围为-1~+1，正号表示正相关，负号表示负相关，零表示不相关，相关系数绝对值越靠近1，敏感性越强。Spearman 秩相关系数表达式如下：

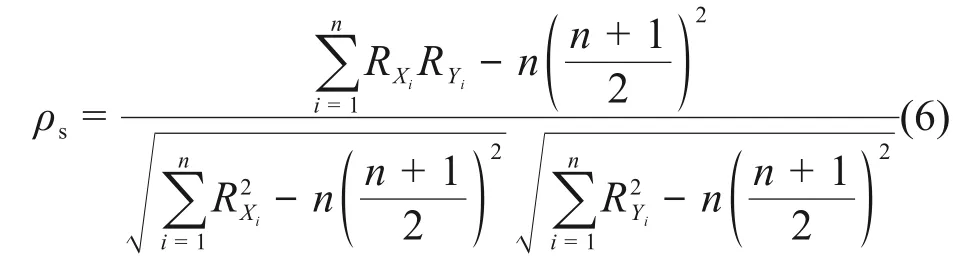
式中：ρs为Spearman秩相关系数；RXi为Xi在X中的大小排序；RYi为Yi在Y中的大小排序；n为样本数。

图8、9 分别为输入参数与包壳最高温度、燃料最高温度的Spearman秩相关系数，深灰色柱状条表示输入参数与目标参数呈正相关，浅灰色柱状条表示输入参数与目标参数呈负相关。由图8、9 可得，燃料制造公差输入参数中，包壳内直径与燃料最高温度、包壳最高温度的相关系数分别为0.345 1、-0.352 2，呈中等相关；热工水力输入参数中，燃料平均温度与燃料最高温度、包壳最高温度的相关系数分别为0.912、0.908 6，呈极强相关，这是由于燃料平均温度自身存在较大的不确定度，且对反应性反馈有直接影响；中子物理输入参数中，第1组衰变常数与目标参数的相关系数分别为-0.619 4、0.565 2，功率与目标参数的相关系数分别为0.386、-0.241 1，均呈中度相关；燃料多普勒常数与目标参数的的相关系数分别为0.934 5、0.945 6，径向膨胀系数与目标参数的的相关系数分别为0.703、0.742 2，轴向膨胀系数与目标参数的的相关系数分别为0.477 99、0.554，说明反应性反馈系数对目标参数具有较高的灵敏度，这是由于其自身存在较大的不确定度，且反应性反馈系数是引发UTOP工况的主要参数。

图8 不确定性输入参数与包壳最高温度的Spearman秩相关系数Fig.8 Correlation coefficient of Spearman rank between the input parameters and peak cladding temperature

图9 不确定性输入参数与燃料最高温度的Spearman秩相关系数Fig.9 Correlation coefficient of Spearman rank between the input parameters and peak fuel temperature

综上所述，在SNCLFR-10 堆的UTOP 事故中，显著影响燃料、包壳峰值温度的输入参数包括包壳直径、稳态燃料平均温度、初始功率、第1 组衰变常数以及反应性反馈系数；其中燃料平均温度以及反应性反馈系数对瞬态安全参数的影响最大。

4 结语

本工作基于CFD/PFS 程序开展了小型自然循环铅铋快堆SNCLFR-10 的无保护超功率瞬态事故不确定性分析，并研究了输入参数对瞬态安全参数的影响程度。结论如下：

1）基于非参数统计法的不确定性计算，得到的目标参数95/95不确定带能够较好地包络名义值；对比目标参数不确定性包络带，可得不确定性输入参数传播到输出参数的不确定性随时间而变化；包壳峰值温度95/95 容忍上限值为1 208.66 K，燃料峰值温度的95/95容忍上限值为2 757.25 K。

2）通过Spearman 相关系数法对SNCLFR-10 的UTOP 事故进行敏感性分析。结果表明：包壳内直径、稳态燃料平均温度、初始功率、第1 组衰变常数以及反应性反馈系数显著影响燃料和包壳峰值温度，其中燃料平均温度和反应性反馈系数对瞬态安全参数的敏感度最强。

作者贡献声明余清远：实施研究，文章撰写；漆静雯：采集数据，分析/解释数据；赵鹏程：统计分析，获取研究经费；赵亚楠：对文章的知识性内容作批评性审阅；于涛：行政、技术支持，指导，支持性贡献。