热管冷却反应堆堆芯瞬态热力耦合研究

刘 博 刘利民 丁冠群 肖 瑶 顾汉洋

（上海交通大学核科学与工程学院 上海200240）

随着世界各国对空间、深海探测需求的逐渐提高，相对于传统动力方式，能量密度更高、适应环境能力更强的核动力电源成为了航天和深海探测任务的更优选择。热管冷却反应堆是目前引起关注的核反应堆电源之一，燃料裂变产生的热量通过热管传导至热电转换装置［1］，与常规反应堆相比结构更简单紧凑，省略了泵、阀等部件，热管散热具有非能动性和优良启动特性［2-3］，能够实现更高的可靠性和安全性［4］。

在高温运行时热管冷却反应堆的热膨胀效应和热应力效应显著，因此在堆芯设计阶段必须考虑热工、应力安全问题。Kapernick 等［5］针对SAFE（Safe Affordable Fission Engine）热管冷却反应堆（SAFE-100）通过有限元软件COSMOS 和SINDA/FLUENT耦合计算获得堆芯温度场和热应力。Wang 等［6］提出了小型热管冷却反应堆（small Heat Pipe cooled Reactor，sHPR），开发了热管冷却反应堆热工水力分析程序用于分析sHPR 的稳态和瞬态性能，得到各关键部件热工参数，并对热管冷却反应堆的典型事故进行了分析和评价，包括功率变化、单根热管失效、冷却通道堵塞等情况。张文文等［7］针对新型空间热管反应堆采用计算流体力学软件FLUENT 对堆芯进行了稳态热工安全分析，对控制转鼓7 种不同角度下的正常工况以及单根热管失效的事故工况进行计算分析，得到最热通道各层材料的温度分布。马誉高等［8］提出了一种考虑热管堆固体堆芯显著膨胀的几何更新和反应性反馈方法，并构建了基于动态几何的中子物理/热工/力学三场核热力耦合分析程序，基于此方法对MegaPower 热管堆进行了核热力耦合分析。

虽然关于热管冷却反应堆热工、力学特性的问题已有很多研究，但大多数研究没有考虑核热力的耦合效应，也很少有堆芯事故瞬态变化情况的研究。基于以上问题，本文基于有限元分析软件FLUENT以及MECHANICAL针对堆芯的典型发热单元分别进行核热力耦合分析，采用点堆中子动力学模型进行堆芯功率、温度场的瞬态计算；并最终基于温度场和力学场分布特征开展堆芯设计以及事故工况下的安全评估。

1 耦合数值方法

1.1 核热耦合模型

1.1.1 点堆中子动力学模型

对NUSTER（Nuclear Silence ThermoElectric Reactor）反应堆进行瞬态核热耦合分析时，反应堆燃料装载量较少，堆芯状态位于临界附近且中子密度随时间变化较缓慢，因此，可采用考虑6组缓发中子的点堆动态方程来求解瞬时燃料棒裂变功率［9］。点堆动力学模型描述了反应堆中子密度与反应性之间的瞬时变化关系，该模型忽略空间效应，计算简便、响应快速。点堆动力学模型见式（1）、（2）：

式中：P(t)为裂变功率，W；ρ(t)为随时间变化的反应性，$；β为缓发中子份额；Λ为平均中子代时间，s；λ为衰变常数；C(t)为缓发中子先驱核浓度；下标i代表第i组缓发中子。

使用全隐式一阶泰勒多项式积分方法对点堆动力学方程进行求解，既可以解决刚性问题，又具有精度高、适用性强的特点［10］。因此，本文采用全隐式一阶泰勒多项式积分法，将显式数值求解后的点堆中子动力学模型基本方程编入FLUENT 软件的用户自定义函数（User Defined Function，UDF）中，以实现在FLUENT软件内的核热耦合迭代计算。

1.1.2 反应性反馈模型

本文研究对象物理模型考虑的反应性反馈主要包括燃料反应性反馈以及导热基体反应性反馈，计算过程中的系统反应性变化如式（3）、（4）所示：

式中：ρ(t)为总反应性，$；ρ0为初始反应性；ρex(t)为外部引入反应性，$；ρi(t)为堆内各材料反馈反应性，$，包括燃料多普勒效应反应性反馈ρU和基体膨胀效应反应性反馈ρMo。

UO2燃料芯块中，燃料温度效应主要是由燃料核共振吸收的多普勒效应引起的。温度升高使燃料中有效共振吸收增加，有效增殖系数下降，产生负的反应性反馈，如式（5）所示：

式中：αDoppler为多普勒温度系数，$·K-1；TF，avg(t)为t时刻燃料棒平均温度，K；TF，avg(0)为正常稳态时的燃料棒平均温度，K。

导热基体由于温度变化会产生材料密度变化、热膨胀造成的尺寸变化等效应，这些效应产生的基体反应性反馈由式（6）给出：

式中：αMo为基体温度反应性系数，$·K-1；TMo，avg(t)为t时刻基体的平均温度，K；TMo，avg(0)为正常稳态时的基体平均温度，K。

1.2 热力耦合模型

热管堆区别于其他传统堆型最显著的特征是其堆芯的固态属性，因此热膨胀效应和热应力问题是其研究的重点［1］。热应力问题的研究主要在于确定温度场以及由温度场确定应力应变。物体内部的温度差ΔT(x，y，z)将引起αTΔT(x，y，z)的热膨胀，则该弹性物体的物理方程变成了式（7）所示：

式中：σi为应力分量，Pa；εi为形变分量，m·m-1；αT为热膨胀系数，K-1；E为弹性模量，Pa；G为切变模量，Pa；μ为泊松系数。

2 计算模型及参数

2.1 几何模型及边界条件

本文研究对象为一种典型热管冷却反应堆——静默式海洋热管冷却反应堆［11］，堆芯主要包括导热基体、燃料棒、热管、轴向反射层、滑动反射层、控制棒组件等［12］。NUSTER堆芯可划分为109个由燃料棒、导热基体以及中心热管构成的发热单元［13］，发热单元于堆芯中的选取方式及发热单元示意图如图1所示。由于开展全堆芯模拟计算量巨大，故建立发热单元的三维模型如图2 所示作为研究对象；为了完整模拟热管区域的传热，对热管蒸发段以及堆芯外部分的热管绝热段、冷凝段进行建模，模拟堆芯到冷源的完整传热过程。NUSTER堆芯燃料区内部分结构尺寸参数以及组件材料选择如表1所示。

表1 燃料区内结构参数Table 1 Design parameters of fuel area

图1 发热单元示意图Fig.1 Schematic diagram of heat unit

图2 发热单元三维模型Fig.2 Schematic diagram of three-dimensional model of heat unit

根据实际情况和物理意义，边界条件设置如下：热分析中边界条件为热管冷凝段壁面为定壁温条件。力学分析中边界条件设置为侧面为对称边界条件，两个顶面和底面为轴向位移约束边界条件，如图3所示。

图3 力学边界条件Fig.3 Mechanical boundary condition

2.2 物性参数

在热分析中涉及的各部件材料热物性相关参数［14-16］如表2 所示，物性在FLUENT 软件中由用户自定义程序UDF编写给出。

表2 材料热物性参数Table 2 Thermophysical properties of materials

其中热管蒸汽区导热系数［15-16］如式（8）所示：

式中：k为蒸汽导热系数，W·（m·K）-1；R为蒸汽区热阻，K·W-1；Leq为热管等效长度，m；μv为蒸汽动力黏度，Pa·s；Tv为蒸汽温度，K；dv为蒸汽区直径，m；ρv为蒸汽密度，kg·m-3；hfg为汽化潜热，J·kg-1。

在MECHANICAL软件中设置各固体材料的力学物性参数，UO2热膨胀关系与塑性区的应变应力方程［17］分别如式（9）、（10）所示，其余力学物性参数如表3所示。

表3 材料力学物性参数Table 3 Mechanical properties of materials

式中：T为温度，K，范围为300~2 873 K；Δl为相对于 300 K时的线性热膨胀。

式中：σ为塑性变形阶段的应力，MPa；εp为塑性变形 阶段的应变，m·m-1。

瞬态计算中，考虑核反应堆中子动力学和多普勒反应性反馈、导热基体温度反应性反馈等，以及通过堆芯物理计算得到的NUSTER 的堆芯反应性反馈系数表达式如表4所示。

表4 NUSTER中子动力学参数Table 4 Neutron dynamic parameters of NUSTER

2.3 网格划分

热分析采用六面体网格划分，轴向网格拉伸，力分析采用六面体与四面体结合的网格划分；发热单元网格划分示意图分别如图4（a）、（b）所示。两种网格划分均满足网格无关性，网格敏感性计算结果分别如图5（a）、（b）所示，据此热分析网格数量约为200万，力学分析网格数量约为28万。

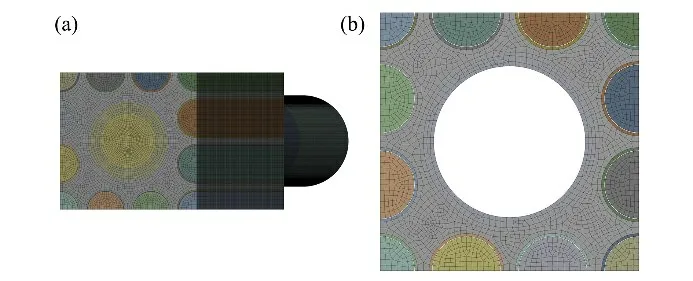
图4 网格划分示意图 (a)热分析网格，(b)应力分析网格Fig.4 Schematic of mesh (a)Mesh of heat transfer analysis,(b)Mesh of mechanical analysis

图5 网格敏感性结果Fig.5 Results of mesh sensitivity

3 热力耦合结果

NUSTER 系统采用4 组滑动反射层和4 个安全控制棒作为初级反应性控制系统，当控制系统发生故障或者外界因素干扰时，控制棒可能会意外抽出（提棒事故）或失控弹出（弹棒事故）而引入正反应性。反应性引入事故是造成瞬态超功率事故的典型事故之一，因此有必要研究热管冷却反应堆NUSTER 在正反应性引入事故情况下的瞬态特性，对堆芯安全性进行验证。NUSTER堆芯中控制棒的价值共约800×10-5，假定弹棒事故发生时在5 s 内线性引入400×10-5反应性，无外界扰动。针对典型稳态工况以及上述反应性引入事故工况，进行热力耦合分析。

3.1 稳态工况结果

反应性引入事故发生前稳态工况的发热单元温度场结果如图6所示，温度峰值为1 516 K。此时发热单元和各组件的等效应力场如图7 所示，图7（a）为发热单元的总体等效应力云图剖面图，峰值为196 MPa 位于包壳；图7（b）为包壳组件的等效应力云图，显示等效应力峰值位于包壳内边缘尖角。图7（c）为导热基体的等效应力分布情况，峰值同样位于基体外表面的棱角处，发生了应力集中，峰值为162 MPa，其余位置等效应力为120 MPa 左右。图7（d）展示了热管壁的等效应力分布情况，峰值为177 MPa，位于热管内壁面。

图6 稳态工况温度云图Fig.6 Temperature contour under steady condition

图7 稳态工况等效应力场云图 (a)发热单元，(b)包壳，(c)导热基体，(d)热管壁Fig.7 Equivalent stress contour under steady condition (a)Heat unit,(b)Claddings,(c)Matrix,(d)Heat pipe wall

3.2 事故工况结果

堆芯反应性和功率以及主要组件温度峰值的变化趋势分别如图8所示。200 s时开始引入外部反应性，燃料棒功率随着总反应性的增加而增大，芯块温度也逐渐升高。各组件温度升高后，在燃料负反馈效应和基体负反馈效应引入的负反应性作用下，总反应性约在220 s 达到峰值后逐渐降低。由于堆芯导热相对于反应性和功率的瞬变更加缓慢，有一定的滞后性，反应性会继续下降至负值；因此各组件温度会缓慢升高至约250 s达到峰值，之后温度开始小幅度降低。最终约在350 s时，反应性、功率、组件温度等参数达到新的稳定状态。引入正反应性事故下八分之一堆芯最终的稳定功率为194 kW，约为初始稳定状态的1.5倍。

图8 反应性(a)和功率(b)瞬时变化Fig.8 Transient variation of core reactivity(a)and core power(b)

图9给出了从稳态工况到事故发生后主要组件的温度峰值变化情况。结果表明：事故过程中燃料芯块温度峰值1 700 K，比初始稳态升高了220 K；包壳温度峰值1 415 K，比初始稳态升高了109 K；热管壁1 364 K，比初始稳态升高了90 K。将各组件温度峰值与各材料的熔点进行比较，结果汇总于表5，结果表明各组件距离熔点均有200 K 以上的安全裕度，事故工况下的堆芯热工安全得到验证。

表5 事故工况下各组件温度峰值Table 5 Peak temperature value of each assembly under accident condition

由图9 可得，260 s 时发热单元各组件出现温度峰值，基于热应力的保守性计算选取此时刻展示温度与热应力的分布情况，温度云图以及等效应力云图分别如图10、11所示。通过比较不同组件在稳态工况和引入事故工况的等效应力峰值，得到反应性引入事故对应力分布的影响并进行安全评估。此时单元温度峰值为1 700 K，等效应力峰值为334 MPa，位于导热基体。图11（a）为发热单元等效应力剖面图，云图表明基体与热管壁的等效应力比其他组件高；图11（b）为包壳组件等效应力云图，峰值为327 MPa；图11（c）为导热基体等效应力分布情况，应力峰值为334 MPa；图11（d）为热管壁等效应力云图，峰值为300 MPa。对比图7、11 的应力结果发现，事故发生后基体等效应力峰值最多增大172 MPa，包壳等效应力最多增大131 MPa，热管壁峰值增大了123 MPa。

图9 组件温度峰值变化Fig.9 Variation of assembly peak temperature

图10 引入反应性事故工况（t=260 s时）温度云图Fig.10 Temperature contour under reactivity insertion accident condition(t=260 s)

图11 反应性引入事故（t=260 s时）等效应力场云图 (a)发热单元，(b)包壳，(c)导热基体，(d)热管壁Fig.11 Equivalent stress contour under reactivity insertion accident condition(t=260 s)(a)Heat unit,(b)Claddings,(c)Matrix,(d)Heat pipe wall

为了更细致地研究事故对不同组件等效应力分布的影响，分别沿包壳和热管壁选择90°、360°的周向路径如图12（a）、（b）所示，另外选择径向截面上燃料芯块到热管壁的径向路径如图12（c）所示。

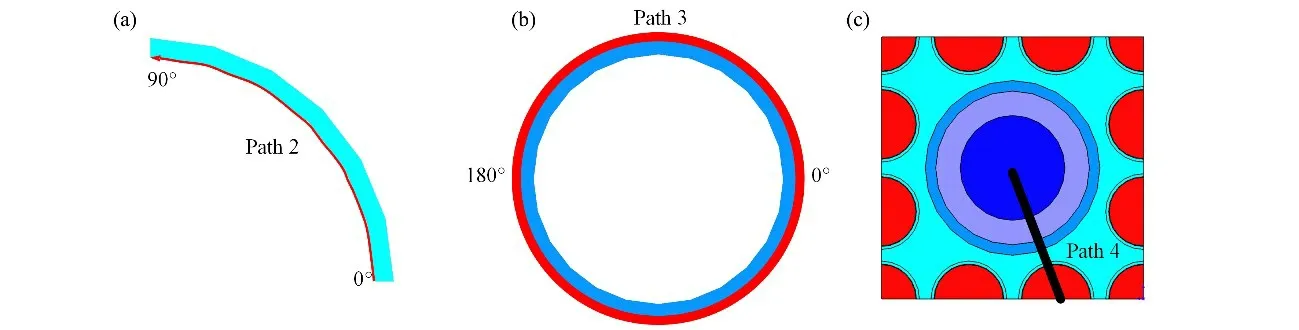
图12 周向路径选取示意图 (a)包壳周向路径，(b)热管壁周向路径，(c)单元径向路径Fig.12 Schematic diagram of Circumferential paths selection (a)Circumferential path along cladding,(b)Circumferential path along heat pipe wall,(c)Radial path in unit

分别作这三条路径上两种工况下的等效应力分布曲线，对比结果分别如图13（a）、（b）、（c）所示。图13（a）结果表明，引入反应性事故会造成包壳上等效应力的增大，在30°、60°位置等效应力差值最大，约为200 MPa。热管壁上周向路径的等效应力对比结果如图13（b）所示，事故工况下的热管壁等效应力明显大于稳态工况下的，在kπ/2（k=0，1，2，3）处等效应力差值最大，约203 MPa。从燃料芯块到热管壁径向路径上的等效应力分布如图13（c）所示，结果表明反应性引入事故下沿径向路径上各组件的等效应力均大于稳态工况下，燃料芯块内区等效应力差值约205 MPa，热管壁差值最大约156 MPa。

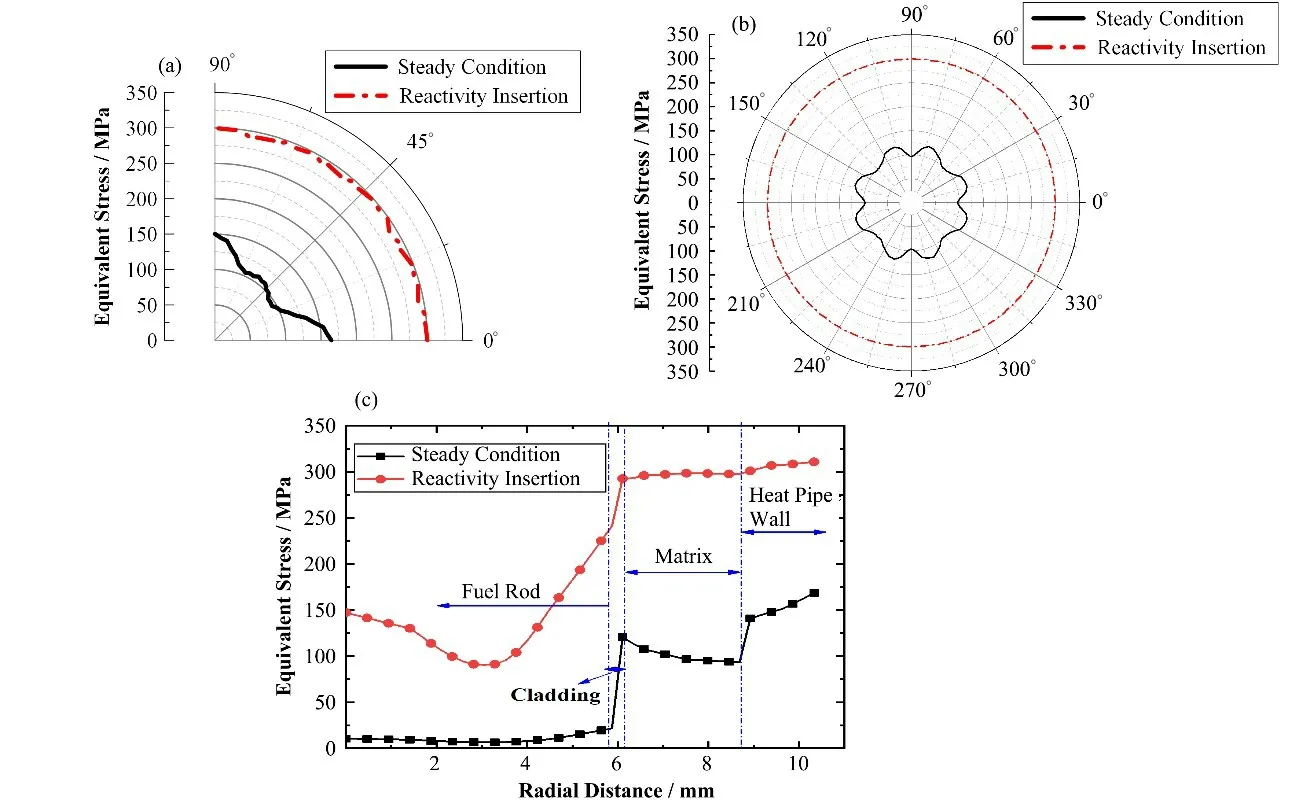
图13 反应性引入事故与稳态工况等效应力比较(a)沿包壳周向路径曲线，(b)沿热管壁周向路径曲线，(c)沿发热单元径向路径曲线Fig.13 Comparison of equivalent stress between reactivity insertion accident and steady condition (a)Curve of circumferential path along cladding,(b)Curve of circumferential path along heat pipe wall,(c)Curve of radial path in heat unit

基于上述温度、应力结果，进行事故工况下的堆芯安全评估。各组件温度峰值变化情况已由图10给出，表5 也表明各组件温度均远小于相应材料的熔点，事故下堆芯热工安全得到验证。依据弹塑性力学强度理论中的von-Mises屈服条件［21］，组件应力峰值与材料屈服强度对比结果总结于表6 中，关键组件等效应力峰值均远小于相应材料的屈服强度，符合von-Mises屈服条件；并且组件应力距限值均有150 MPa 以上的安全裕度，因此组件应力方面满足强度要求。

4 结语

基于有限元分析软件ANSYS平台，结合点堆中子动力学模型，针对两种工况——稳态工况与反应性引入事故工况，对静默式海洋热管冷却反应堆NUSTER堆芯中的典型发热单元开展了核热耦合以及热力耦合计算，给出了发热单元温度场、应力场以及反应性、功率的瞬态变化结果等。结果表明：事故工况发生后各组件的温度、等效应力均有明显增大，对事故工况下的发热单元进行温度、应力安全评估，对比结果表明各组件均满足热工、应力的限制要求；并且事故下各组件温度有200 K 以上的安全裕度，等效应力距离安全限值有150 MPa 以上的安全裕度，证明了NUSTER堆芯设计在稳态和事故工况下的可靠性和安全性。

作者贡献声明刘博：实施研究计算与数据处理，起草文章；刘利民：设计研究方案与指导；丁冠群：提供软件技术指导；肖瑶：提供总体技术指导；顾汉洋：获取研究经费，提供平台支持。